极值分析下基于位置矩阵的质心定位方法
2021-08-23张志利周召发姚鑫玲
段 辉,张志利,周召发,梁 哲,姚鑫玲
(1.火箭军工程大学导弹工程学院,陕西 西安 710025;2.火箭军工程大学兵器发射理论和技术国家重点学科实验室,陕西 西安 710025)
0 引 言
星敏感器是目前精度最高的姿态敏感器之一,其以距离无穷远的恒星为基准,可以获得角秒级的定姿精度。星点提取作为星敏感器的关键技术之一,其算法的优劣直接影响着星图识别算法的识别效果。
目前,针对星点质心定位,国内外学者主要从误差产生的机理出发展开相关研究。Salomon[1-2]等人基于大量的实测数据分析发现,该误差用正弦函数拟合时具有较高的拟合优度,并基于该特性对误差进行相应补偿。Stanton[3-5]等人通过理论推导发现质心法改进之后,其误差并不全是高斯白噪声,仍然存在固定的系统误差,并通过标定降低了该系统误差的影响。Grossman[6]等人开拓性地引入了高斯模型以描述星点能量分布,并结合理论分析与仿真实验定量确定出质心定位误差与恒星星等、拍摄星图的信噪比等因素之间的关系。Li[7]等人首次将加权思想引入到质心定位中,并研究了不同强度的加性噪声和乘性噪声对加权质心法的影响。Alexander[8]等人摒弃传统的空域分析方法,转而从频域的角度进行误差分析与建模,从理论上证明了质心定位误差会随着星点模糊而降低,但是通过大量实验发现当模糊区域超过某一临界值时,其系统性误差反而开始增加,对于该现象,其建立的模型无法给出合理的解释。Fisher[9]等人推导了质心定位的系统性误差与星点弥散区域范围之间的理论关系,实验表明其所确定的最佳星点弥散区域具有一定的定位精度,但是该方法对星点能量分布模型等进行了较多简化,无法运用于高精度领域。姜亮[10]等人将传统的高斯模型替换为Giancarlo模型,并从频域的角度分析基于Giancarlo模型的误差传递形式。谭迪[11]等人通过对光学平台的各项参数进行单独建模,再结合大量的数值仿真实验,准确得到了质心定位的系统性误差与光学平台的各项参数之间的定量关系。曹阳[12]等人指出像素位置偏差也是造成系统性误差的重要原因之一,并推导了其误差传递模型,实验表明高精度的标定可以基本消除该因素的影响。
在星点提取算法方面,Kim[13]等人基于遍历整幅星图的思想,提出了扫描法。但该算法所提取的星点像素数量会随着噪声的增加而快速增加,进而导致后续的星点像素聚类过程十分耗时。Mortari[14]等人提出的矢量法在星图受到较严重的噪声污染时,其提取的星数会迅速达到预设值,而且当某行(列)存在多个星点时,整数矢量只能存储灰度值最大的那个点。田玉龙[15]等人提出的局部熵法以图像不同位置的局部熵大小来敏感所寻目标,在星点所处区域,其局部熵会由于该区域的灰度不均匀而发生突变,最小熵值位置即为恒星星点所处位置。余路伟[16]等人针对星敏感器在轨运行时面临的复杂恶劣环境问题,提出了背景自适应预测算法。该算法以星点区域与背景区域的性质差异为基准分配权值,并提出了一种旋转对称掩膜以解决杂散光与星点区域完整性问题。Luo[17]等人提出的灰度交叉投影法的计算量明显降低,但是当不同星点的投影区域存在重叠时,将会导致星点的邻接矩形变大,会有更多的独立噪声点参与质心计算,严重影响星点提取精度。针对上述传统的星点提取算法的局限性,本文结合极值分析下的星点弥散区域粗提取算法与基于位置矩阵的线段编码标记法进行星点提取,既能保证较高的星点提取精度,又能满足工程上对算法的实时性与对噪声的鲁棒性要求。
本文高精度星点提取流程如下:① 针对去噪后的星图,从投影差分的角度出发,利用所提极值分析下的星点弥散区域粗提取算法,找出各星点的内部所属像素,进而得到星像区域的概略位置;② 基于位置矩阵的线段编码标记法采用边扫描边合并的方式,仅通过一次扫描完成对所有星点的连通区域标记,并有效剔除噪点;③ 采用高斯曲面拟合法计算出星点质心坐标。
1 星图去噪
星点目标的尺寸非常小且没有形状、纹理等特征,星敏感器拍摄的星图本身又具有较低的信噪比,因而投影到像平面的星点像素区域极易被噪声和背景所淹没。
本文重点不在星图去噪上,所以下面简要叙述星点提取时采用的去噪方法。本文采用文献[17]提出的改进多窗口抽样自适应阈值选取方法,根据实时得到的星图确定阈值,既能够有效去噪,又不会耗时过多。首先,选取大小适当的抽样窗口,其确定原则如下:为了快速得到分割阈值以降低星图去噪的处理时间,抽样时所有抽样窗口的像素之和一般为星图总像素的4%~8%,抽样窗口数目一般取30~50且各个抽样窗口的位置尽可能分布均匀,抽样窗口的像素之和与抽样窗口数目之间的比值即为抽样窗口大小。然后,在星图的不同位置选取抽样窗口,计算该抽样窗口的灰度均值和标准差,多次重复上述过程,最后综合考虑所有抽样窗口的数据,以确定出分割阈值。从上到下,从左到右依次扫描星图图像中的各个像素,大于该分割阈值的视为潜在的星点像素,后续会进行相关处理,否则视为背景像素,予以剔除。多窗口抽样的核心公式如下所示:
(1)
式中:Nw为抽样窗口的个数;μi和σi分别是第i个抽样窗口中所有像素的均值和方差;α为经验值,一般取3~5。
2 星点局部区域限定
近年来,学者们纷纷提出了许多优秀的图像分割算法[18-23],但由于星图图像的特殊性,大多数算法的星点提取效果并不理想。因此,本文从投影差分的角度出发,提出极值分析下的星点弥散区域粗提取算法,实现初步的星图图像分割。在星点内部某像素位置已知的情况下,下一步的星点内部像素精提取便会具有更高的准确性和更快的搜索速度。极值分析下的星点内部像素确定算法如下:对于星敏感器拍摄的一幅M×N大小的星图,先进行纵向的投影,即对每一列中所有像素点的灰度值求和,得到关于x的投影函数S(x)如下所示:
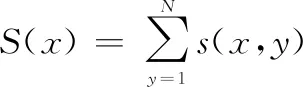
(2)
式中:x为像素点的横坐标;y为像素点的纵坐标;s(x,y)为坐标(x,y)处的像素点灰度值;M为星图的行数;N为星图的列数。
得到投影函数S(x)后,在整个取值范围内对S(x)进行前向一阶差分运算,得到差分函数P(x)如下所示:
P(x)=S(x+1)-S(x)
(3)
遍历差分函数P(x)的所有项,若存在相邻两项满足:
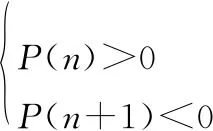
(4)
则说明点x=n+1为投影函数S(x)的极大值点,找出所有的极大值点作为候选。星图经纵向投影得到星点的横坐标范围,通过差分函数P(x)找出所有极大值点,然后对以横坐标范围为界的条状区域进行横向投影,即可得到该条状区域内的星点个数和纵坐标范围。取极大值点作为星点内部像素的候选横坐标,纵坐标范围的中点作为星点内部像素的候选纵坐标。那么可以给出结论,即使在纵向投影时出现两颗星点存在重叠的现象,也一定存在某一个候选横坐标(极大值点),使得该候选横坐标既落在星点1的的横坐标区域,又落在星点2的横坐标区域;或者存在某两个候选横坐标(极大值点),使得一个落在星点1的的横坐标区域,另一个落在星点2的横坐标区域。此时,候选横坐标与候选纵坐标的两两组合之中,一定会同时出现星点1的内部像素点和星点2的内部像素点。具体的证明在后续给出。
算法的具体步骤如下。
步骤 1利用式(2)对M×N大小的星图进行纵向的投影,得到投影函数S(x)。
步骤 2利用式(3)对S(x)进行前向一阶差分运算,得到差分函数P(x)。
步骤 3遍历差分函数P(x)的所有项,找出所有的极大值点作为候选横坐标,这些候选横坐标中一定存在某一个值同时落在星点1和星点2的横坐标区域内。
步骤 4星图经纵向投影得到星点的横坐标范围,然后对以横坐标范围为界的条状区域进行横向投影,可得到该条状区域内的星点个数和纵坐标范围。取纵坐标范围的中点作为星点内部像素的候选纵坐标。候选横坐标与候选纵坐标任意组合得到所有候选的星点内部像素坐标,判断每一个候选坐标的邻域,筛选出最终的星点内部像素坐标。以该星点内部像素坐标为中心,δ为半径的某个矩形区域即为星点粗提取结果,δ取值一般较大。
下面从理论上证明两颗星点的纵向投影重叠时,一定存在某一个候选横坐标(极大值点),使得该候选横坐标既落在星点1的横坐标区域,又落在星点2的的横坐标区域;或者存在某两个候选横坐标(极大值点),使得一个落在星点1的横坐标区域,另一个落在星点2的横坐标区域。两颗星点横向投影发生重叠时的情况类似。
星点光斑在电荷耦合器件(charge coupled device,CCD)平面上的能量分布服从二维正态分布,对星点光斑进行纵向投影,可理解为求该二维正态分布的边缘分布。由概率论的知识可知,二维正态分布的边缘分布一定也为正态分布,此处不加以证明。所以,原问题抽象出来的数学模型为
(5)
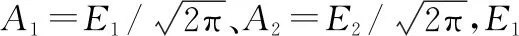
3σ以外的能量占比很小,这一部分的像素点的灰度值非常小,远远小于去噪阈值,在星图去噪时会被直接置0。所以函数f1(x)和f2(x)在分析时可以看作是截断函数,即取值范围严格为[μ-3σ,μ+3σ],函数在取值范围内连续。
当正态分布f1(x)和f2(x)的均值和方差满足:
(6)
存在图1中的5种重叠情况。
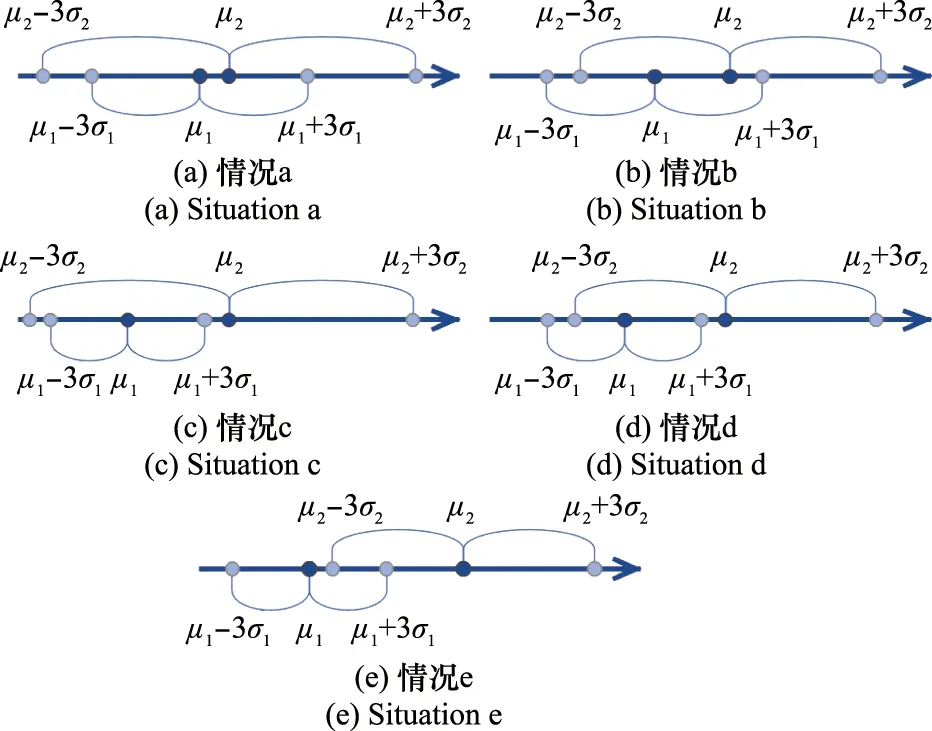
图1 第一类正态分布函数重叠示意图Fig.1 Diagram of the first kind of normal distribution function overlap
第一类5种情况下重叠区域的取值范围如下所示:
(7)
当正态分布函数f1(x)和f2(x)的均值和方差满足:
(8)
存在图2中的5种重叠情况。

图2 第二类正态分布函数重叠示意图Fig.2 Diagram of the second kind of normal distribution function overlap
第二类5种情况下重叠区域的取值范围如下所示:
(9)
数学模型经上述步骤细化后,研究问题变为:证明上述10种情况中的每一种都存在一个极大值点,且该极大值点恰好落在星点1和2纵向投影的重叠区域范围内,即该极大值点既落在星点1的横坐标范围内,又落在星点2的横坐标范围内。
需要强调的是,正态分布函数f1(x)和f2(x)不同的重叠形式所对应的函数表达式F(x)也不尽相同,如图3中的两种情况所示,其中实线部分为f1(x),虚线部分为f2(x)。

图3 函数表达式差异化示意图Fig.3 Diagram of function expression differentiation
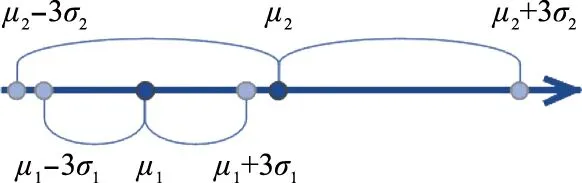
图4中的两种情况对应函数表达式F(x)从左到右可分为F1(x)、F2(x)、F3(x)3段,分别如下所示:
(10)
(11)
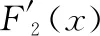
(12)
可以看出,求解极值点的解析解会非常困难,而且解析解中会同时包含未知参数E1、E2、μ1、μ2、σ1、σ2,导致无法判定解析解是否在重叠区域取值范围内。因此,这种思路行不通。既然无法通过求解精确的解析解来证明极值点是否存在于重叠区域之中,那么换种思路,转而去证明这10种情况都存在两个极大值点分别落在函数f1(x)和f2(x)的横坐标范围内,或者存在1个极大值点落在函数f1(x)和f2(x)重叠区域内,且必须是极大值点。
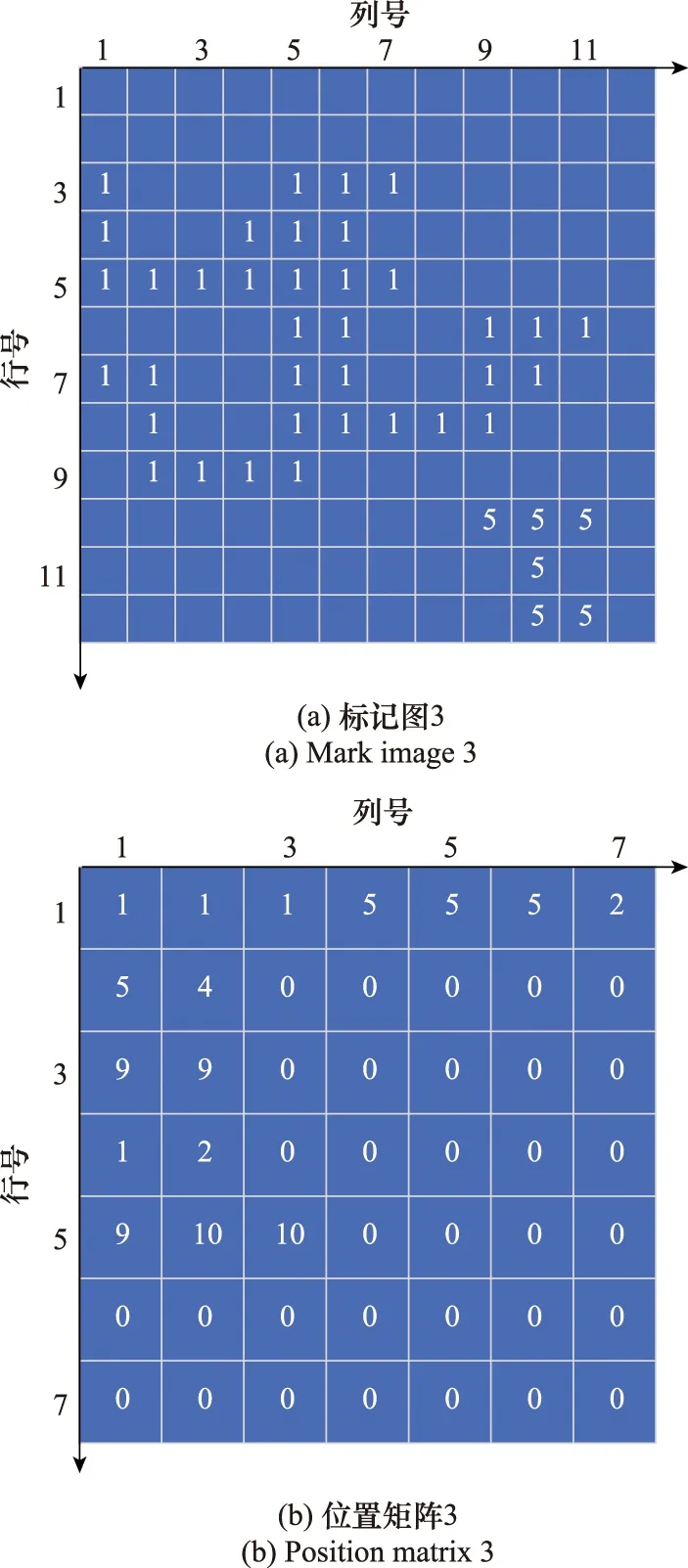
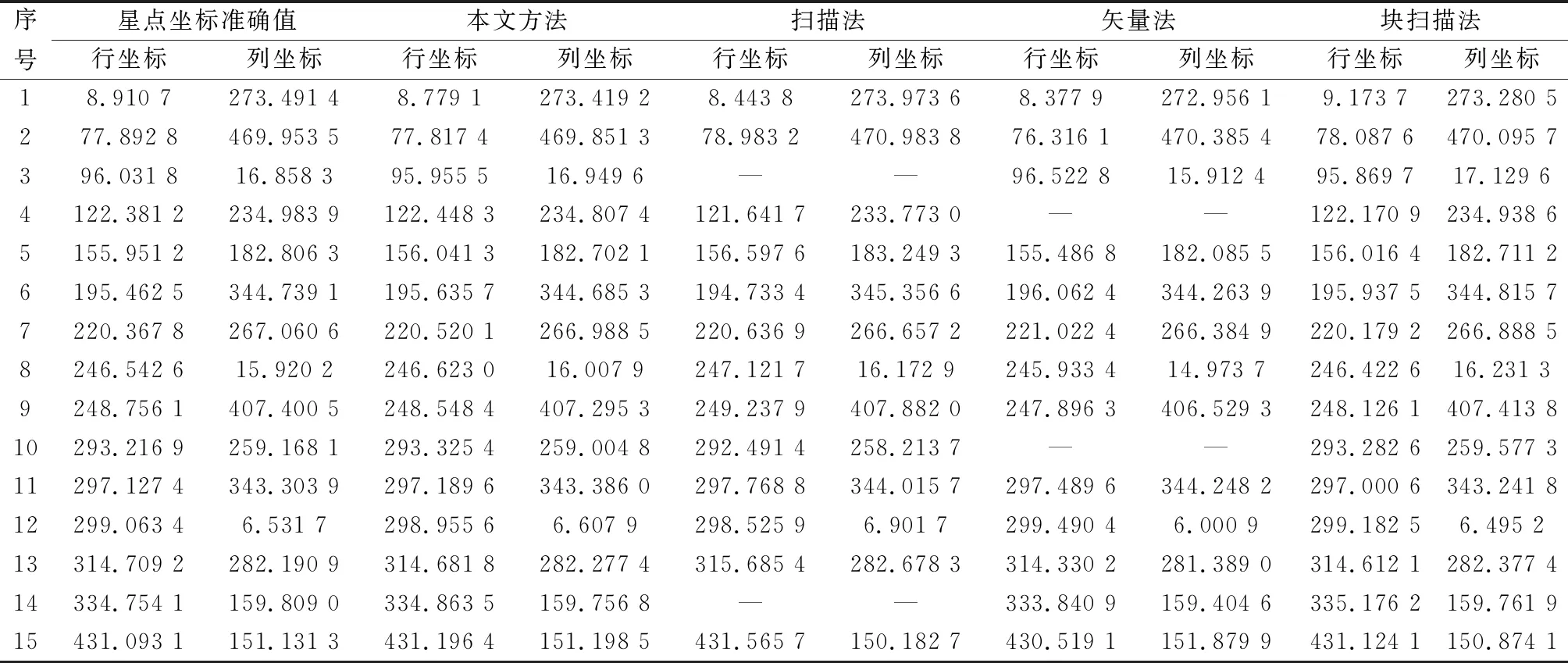
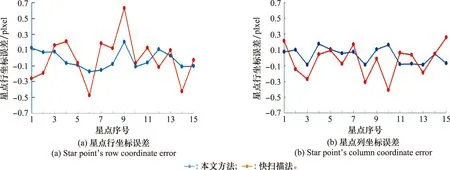
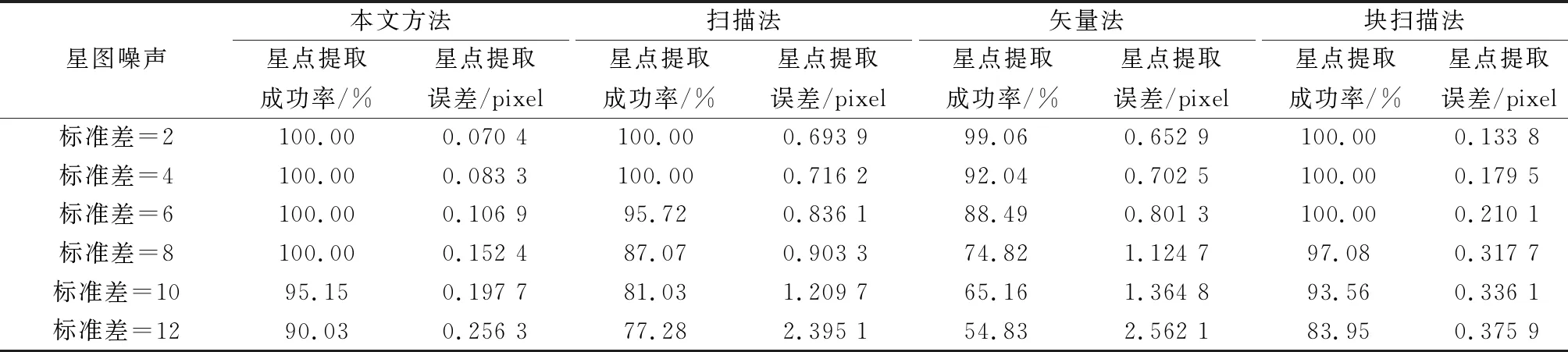
可以知道,原函数F(x)和导函数F′(x)在定义域内均为连续函数,则只要能够证明某开区间上都存在实数m和n,且满足m 考虑图1中情况a,函数F2(x)的定义域为x∈(μ1-3σ1,μ1+3σ1),且满足μ1≤μ2、σ1≤σ2,如图4所示。 图4 图1中情况a示意图Fig.4 Diagram of situation a in Fig.1 (13) 若满足,则说明存在1个极大值点落在函数F2(x)的定义域内。 证毕 (14) 证毕 考虑图1中情况b,函数F2(x)的定义域为x∈[μ2-3σ2,μ1+3σ1],且满足μ1≤μ2和σ1≤σ2。不难发现,均值点μ1、μ2恰好落在闭区间[μ2-3σ2,μ1+3σ1]中,此时证明过程与结果与图1中情况a完全一致,不再赘述。 考虑图2中情况c,函数F2(x)的定义域为x∈[μ1-3σ1,μ1+3σ1],且满足μ1≤μ2、σ1≤σ2,如图5所示。 图5 图1中情况c示意图Fig.5 Diagram of situation c in Fig.1 由图5可知,此时函数F2(x)的定义域虽然与图1中情况a相同,但是函数分布不同,此时的分段函数形式如下所示: (15) 由于f1(x)>0和f2(x)>0,且f1(x)在区间[μ1-3σ1,μ1]上为增函数,f2(x)在区间[μ2-3σ2,μ2]上为增函数,且f1(μ1-3σ1)为左边界,所以函数F(x)在间断点μ1-3σ1处产生向上的跳变,该间断点无法等价为极大值点;f1(x)在区间[μ1,μ1+3σ1]上为减函数,f2(x)在区间[μ2-3σ2,μ2]上为增函数,且f1(μ1+3σ1)为右边界,所以函数F(x)在间断点μ1+3σ1处产生向下的跳变,则间断点μ1+3σ1即为要找的等价极大值点。虽然等价极大值点μ1+3σ1在断点处,但仍处于f1(x)和f2(x)的重叠区域,满足要求。 证毕 同理,图1中情况d、情况e的证明过程与结果与图1中情况c完全一致,不再赘述。 考虑图2中情况a、情况b,均值点μ1和μ2恰好落在f1(x)和f2(x)的重叠区域中,此时证明过程与结果与图1中情况a完全一致,不再赘述。 考虑图2中情况c,函数F2(x)的定义域为x∈[μ2-3σ2,μ2+3σ2],且满足μ1≤μ2、σ1≥σ2,如图6所示。该情况与图1中情况c略有不同,此时f1(x)>0且f2(x)>0,f1(x)在区间[μ1,μ1+3σ1]上为减函数,f2(x)在区间[μ2-3σ2,μ2]上为增函数,且f2(μ2-3σ2)为左边界,所以函数F(x)在间断点μ1-3σ1处产生向上的跳变,该间断点即为要找的等价极大值点,两种情况产生差异的原因主要是函数f1(x)和f2(x)的单调性区间不同。 证毕 同理,图2中情况d、情况e的证明过程与结果与图1中情况c完全一致,如图3所示。 图6 图3中情况c示意图Fig.6 Diagram of Situation c in Fig.3 至此,10种情况全部证明完毕。在星点1、星点2发生重叠时,总是存在一个极大值点或者等价极大值点落在星点1和星点2的重叠区域。 得到星点像素大概所处的区域之后,还需要进一步精提取星点像素。基于此,本文提出了一种基于位置矩阵的线段编码标记算法。 线段编码标记时,若上下行中两像素线段有交集,则标号相同,反之,则赋予不同标号。判断上下行中两线段是否连通的方法如下所示: xa≤xc≤xb或xc≤xa≤xd (16) 式中:xa、xb和xc、xd分别为上下行中各线段的端点坐标。若满足该不等式,则两条线段连通,否则,不连通。 传统的线段编码标记算法至少需要两次扫描才能完成标记,第一次扫描时记录连通关系,第二次扫描归并具有等价关系的连通体。该方式执行效率低,而且无法规避噪声点的影响。而基于位置矩阵的线段编码标记算法,采用边扫描边合并的方式,仅需一次扫描便可完成对所有星点的连通区域标记,并能有效剔除星图图像中的噪声点。 位置矩阵coor[N×M]的第i行数据,表示编号值为i的线段集合中每一条线段起始点的列坐标。值得注意的是,位置矩阵coor中并未记录线段起始点的横坐标,因为横坐标的值可以在算法的执行过程中自动推算出来。 为了解释更加直观,本节以较为复杂的图8作为原图来说明该算法,图中空白像素的值为0,具体的执行步骤如下。 图7 基于位置矩阵的线段编码标记法示意图1Fig.7 Schematic diagram 1 of line segment coding notation based on position matrix 步骤 1位置矩阵coor的行数取7,列数取7,并将位置矩阵内所有元素初始化为0。对原图的第1行进行线段编码,遇到“0”像素点到非“0”像素点的跳变时,赋予非“0”像素点编号“1”。而该非“0”像素点后面与之相连续的所有非“0”像素点都赋予相同的编号,直到遇到“0”像素点或这一行扫描结束。继续进行该行后续像素点的扫描,若发现线段,进行上述相同的判别操作,对其编号,并且编号值在之前的基础上加1,直至扫描完第1行全部像素,即第1行不会进行标号,位置矩阵coor不变。 步骤 2对原图的第2行进行同样的线段编码,若存在像素线段,则需要对其进行连通性分析。遍历新线段与第1行中所有线段之间的连通关系,若新线段与第1行的多条线段存在连通关系,则需要依赖位置矩阵对具有等价关系的标号类进行归并。由于该矩形区域第2行无目标线段,所以不对其标号,位置矩阵coor不变。 步骤 3对原图的第3行进行线段编码,其第1段线段标号为1。同理,第2段线段标号为2。此时,将第1段线段的起始点列坐标值1赋给位置矩阵coor[1,1],将第2段线段的起始点列坐标值5赋给位置矩阵coor[2,1]。接着,对原图的第4行进行线段编码,第1段线段与上一行中标号为1的线段存在交集,所以标号为1;第2段线段标号为2,将该行中第1段线段的起始点列坐标值1赋给位置矩阵coor[1,2],将第2段线段的起始点列坐标值4赋给位置矩阵coor[2,2]。此时的标记图像和位置矩阵如图7所示,左图为标记图像,右图为位置矩阵。 步骤 4对原图的第5行进行线段编码,该行的唯一线段与第4行的两线段相重合,此时将两线段中较小标号值1赋予新线段,并利用位置矩阵合并等价连通体1和2。首先,找到位置矩阵coor中与编号2所对应的行,即第2行,取其最后一个非0元素值4,即为上一行中编号为2的线段的起始点纵坐标;接着,由于扫描的是第5行,5-1=4,则可以反推出上一行的行数为4,即为第4行中编号为2的线段的起始点横坐标。至此,得到了第4行中编号为2的线段的起始点坐标(4,4),将该像素点及其之后的像素点值置1,直到遇到0像素点停止;然后,取位置矩阵中第2行元素值4前一位的值,该值即为第3行中标号为2的线段的起始点列坐标,列坐标为5。由于扫描的是第5行,5-1-1=3,则可以反推出该起始点横坐标为3。至此,得到了第3行中编号为2的线段的起始点坐标(3,5),将该像素点及其之后的像素点值置1,直到遇到0像素点停止;以此类推,直至将编号为2的目标线段全部更新。继续扫描第6行和第7行,此时的图像和位置矩阵如图8所示。 图8 基于位置矩阵的线段编码标记法示意图2Fig.8 Schematic diagram 2 of line segment coding notation based on position matrix 步骤 5对原图的第8行进行线段编码,第1段线段标为4,第2段线段标为1,并对标号3的线段集合进行合并,依次可得标号3的两条线段的起始点坐标为(8,9)和(7,9),然后分别置1。接着扫描下一行,直至原图扫描完毕,此时的图像和位置矩阵如图9所示。 图9 基于位置矩阵的线段编码标记法示意图3Fig.9 Schematic diagram 3 of line segment coding notation based on position matrix 从图9可以看出,基于位置矩阵的线段编码标记法仅需一次扫描就可标记出所有连通区域。 得到星点精确的像素区域之后,则可以进行星点质心坐标的计算。相较于传统的质心法,高斯曲面拟合法具有更高的精度[24-25]。因此,本文采用高斯曲面拟合法对星点进行质心定位。该算法的核心思想是利用星点区域像素信息估计出高斯曲面参数以得到星点精确的质心坐标,具体原理在此不再赘述。 使用Matlab 2012b仿真软件,对所提方法进行仿真实验验证。 本文采用第4版的SKY2000星表作为基本星表。文中设定导航星的星等小于6 Mv[26]。模拟星图图像的分辨率设为512×512 pixel,星敏感器的视场范围为12°×12°,模拟星图的灰度级为0~255。星图中存在的各种噪声,统一简化为高斯白噪声,不作过多区分。 噪声的影响主要指的是噪声标准差带来的影响[27-31],因此将高斯白噪声均值设置为0,标准差设置为8,得到相应的模拟星图。仿真实验结果如表1所示。从左到右依次为本文方法、扫描法、矢量法、块扫描法的最终质心定位结果,各方法均通过高斯曲面拟合进行最后的质心计算。 表1 星点提取仿真实验结果Table 1 Results of star extraction simulation pixel 从表1中的仿真结果可以看出,在强噪声干扰下,本文所提方法和块扫描法成功地提取出了所有的星像点(15颗),而扫描法和矢量法都只提取出了13颗星点,扫描法未识别出序号为3和14的星点,矢量法未识别出序号为4和10的星点。观察可知,序号为8和9的星点和序号为11和12的星点在行坐标方向部分重叠,但本文所提算法仍然能够将其正确提取,可见本文算法的优势所在。从表1可以粗略看出本文方法和块扫描法星点提取的精度最高。为更直观地看出两种方法的精度差异,通过与各个星点的真值作差得到这两种方法在两个方向上的质心定位偏差,如图10所示。 图10 星点质心坐标误差仿真结果Fig.10 Simulation results of star centroid error 扫描法执行过程中大量的噪声点被误划分为星像点,而星像像素聚类过程往往只选取前30颗最亮的星作为候选导航星[32]。矢量法提取的星数会迅速达到上限,而且当某行(列)存在多个星点时,整数矢量只能存储灰度值最大的那个点。而块扫描法通过满足某条件的像素个数值来搜索星点弥散区域,其抗干扰性能得到较大的提升,但仍易受到噪声点的影响[33]。 本文算法通过极值分析下的星点弥散区域粗提取算法对去噪星图中的星点进行粗定位;然后,利用基于位置矩阵的线段编码标记法,采用边扫描边合并的方式,仅需一次扫描便可完成对所有星点的连通区域标记,并能有效剔除星图图像中的噪声点,且该方法在高精度提取星点质心坐标的前提下,对星点弥散范围较小的弱星仍具有较好的识别效果。因此,较之其他3种方法,本文所提方法具有更好的抗干扰性能。 前文的仿真分析只是在标准差为8的条件下基于一幅星图得出,为了进一步考察本文方法的抗干扰性能并对上述分析进行验证,首先通过设置不同的光轴指向参数,模拟得到500幅不同星图并分别加入不同标准差的高斯白噪声,以检验前述几种方法在不同工作环境下的总体表现水平。星点质心误差计算如下: (17) 式中:Err为星点提取误差;Nm为参与仿真的星图数,此处为500;Ni为星图中正确提取的星点数;(xrj,yrj)为第j个星点的质心坐标标准值,即真实值;(xj,yj)为所提4种算法解算出的星点坐标,即测量值,星点提取结果如表2所示。 表2 不同噪声水平下星点提取结果Table 2 Results of star point extraction in different noise levels 根据上述仿真实验结果,可以明显看出,本文方法在星点提取成功率和星点提取误差两方面都优于其余3种算法,尤其是相较于扫描法和矢量法而言,算法性能提高幅度较大。具体来说,本文方法在星点提取精度方面相比于扫描法平均提高7.9倍;相比于矢量法平均提高8.3倍;相比于块扫描法平均提高1.9倍。仿真结果与前文分析结论相一致。 在星点提取成功率方面,随着噪声强度加大,各算法都不可避免的受到影响。其中,矢量法的抗干扰能力最差,在标准差为2时就已经开始出现部分星点无法提取的情况,且在噪声标准差为12时,提取成功率仅为54.83%,而提取的星点数量急剧减少也影响着后续的定姿精度;扫描法受噪声影响次之,噪声标准差大于4时,星点提取成功率开始下降,噪声标准差为12时,提取成功率为77.28%;块扫描法受噪声影响较小,噪声标准差大于6时,星点提取成功率开始出现下降,且在噪声标准差为12时,提取成功率仍能达到83.95%,体现了其较好的抗噪性能;本文方法的抗干扰能力最强,噪声标准差较小时对算法几乎不造成影响,噪声标准差大于8时,星点提取成功率才开始出现小幅下降,在噪声标准差为12时,还能保证90.03%的高提取成功率。可见本文方法的抗干扰性能明显优于其他3种星点提取方法。 接着对本文方法与扫描法、矢量法、块扫描法的算法复杂度进行简要分析。扫描法聚类过程往往选取前30颗最亮的星作为候选导航星,涉及到最大灰度值的捜索过程,矢量法相应的矢量所存储的是候选星像中心的位置和灰度值,再以星像中心为基础进行候选导航星的确认,且扫描法和矢量法需要多次遍历整幅星图以搜索出特征信息,时间消耗较为严重;而块扫描法避免了全图扫描,且其提取速度与扫描块的大小有关,当扫描块设定不同大小时,其提取速度变化较大。由前文可知,本文方法在搜索星点像素区域时有效避免了多次遍历整幅星图,所以实时性应显著优于扫描法和矢量法。相比于块扫描法,本文综合采用基于距离判别的灰度交叉投影法和基于位置矩阵的线段编码标记法,耗时基本能与之持平。 为了进一步考察本文方法的实时性并对上述分析进行验证,进行了仿真对比实验。对随机生成的500幅星图加入均值为0、标准差为8的高斯白噪声,分别利用本文方法、扫描法、矢量法和块扫描法进行星点提取,统计各自的平均星点提取时间,结果如表3所示。 表3 星点提取时间比较Table 3 Comparsion of star point extraction time s 由表3中的仿真结果可知,4种方法的实时性水平由高到低依次为块扫描法、本文方法、矢量法、扫描法。本文方法与块扫描法的星点提取时间基本相等,扫描法和矢量法的星点提取时间较长,可见仿真结果与理论分析结果相吻合。 仿真实验针对不同的工作环境给出了不同的仿真条件,并从质心定位精度、识别星点的数量水平以及算法处理速度3个方面对本文方法与较常见的扫描法、矢量法、块扫描法进行了性能比对。仿真结果表明,在不同的噪声标准差下,本文方法的星点提取精度和星点提取成功率具有更大的优势。本文方法的星点提取时间基本与块扫描法相等,但与扫描法和矢量法相比,具有显著的优势。总体而言,本文方法在不同的干扰条件下,仍能在星点提取精度、星点提取成功率以及实时性方面保持良好的性能水平。 本文所提方法通过极值分析下的星点弥散区域粗提取算法,对去噪星图进行星点局部区域限定,克服了传统方法难以应用于星点重叠情况的不足,并在提高星敏感器抗噪性能的同时,降低了星点提取算法的内存和时间开销。然后,采用基于位置矩阵的线段编码标记法精确提取星点所有的内部像素,仅需一次扫描便可完成对所有星点的连通区域标记,并能有效剔除星点矩形区域中的噪声点。最后,利用星点区域像素信息估计出高斯曲面参数以得到星点精确的质心坐标。仿真结果表明,星图噪声标准差处于2的水平时,本文的数据处理方法可以使星点质心定位精度达到0.070 4 pixel,且在星图噪声标准差处于12的水平时,仍具有90.03%的高星点提取成功率。相比于传统的星点提取方法,本文方法的星点提取精度和提取成功率均大幅提高,并且星点提取时间仍维持在一个较好的水平。



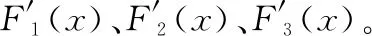
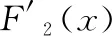


3 星点的精提取


4 仿真实验及分析
4.1 仿真条件设置
4.2 模拟星图仿真实验结果

5 结 论
