伺服机构导管振动疲劳失效分析

2021-08-23刘雅洁张晓莎赵守军

导弹与航天运载技术 2021年4期

王增，兰天，刘雅洁，张晓莎，赵守军

（北京精密机电控制设备研究所，北京，100076）

0 引言

伺服机构与发动机连接，摇摆发动机实现推力矢量控制，是火箭上力学环境条件最恶劣的控制设备。伺服机构有较多金属导管，工作环境激振频率丰富，对导管考验苛刻，导管破裂已成为不可轻视的结构故障。伺服机构在工作过程中，由于存在工况变化、流体流速压力对管道的作用、液压脉动作用等因素，当激振力频率接近导管固有频率时，将发生共振[1～3]，从而导致导管破裂。另一方面，尽管伺服机构导管的结构设计、生产并不存在太大的技术难度，但生产过程中，由于焊接残余应力去除不足、生产和装配工艺不规范等因素的影响，进而产生各种各样的故障。其中振动导致的疲劳失效是常见的故障模式。

针对导管振动疲劳失效故障，很多学者做了研究并给出具有借鉴意义的结论。欧阳芙等[4]对运载火箭增压系统中外径小于15 mm 的小导管进行疲劳分析，给出随机振动条件下小导管的疲劳寿命；舒送等[5]对飞机液压管路中肘形导管根部裂纹故障进行研究，得出管路固有频率与发动机工作频率重合导致共振，并给出改进措施；徐云飞等[6,7]从流固耦合的角度对液体火箭发动机充液导管进行动力学特性研究，得出液体对导管1 阶谐振频率的影响，采用有限元仿真分析的方法，对电子设备在随机振动下的疲劳寿命进行研究，提供了采用有限元计算疲劳寿命的方法；邵闯[8,9]采用试验的方法对金属导管振动疲劳特性进行了研究。然而，伺服机构工作环境恶劣，导管疲劳失效模式复杂，本文针对伺服机构蓄压器导管出现疲劳裂纹问题，开展振动疲劳研究，分析振动频率、工作压力及焊接残余应力对导管疲劳失效的影响并给出改进措施。

1 导管振动模型

伺服机构蓄压器导管为三维空间结构，如图1 所示。导管两端焊接在蓄压器上，伺服机构工作时，液压油从导管的一端流向另一端，柱塞泵产生的压力脉动通过油液作用在导管上，形成简谐激励力F，造成导管在谐波激励下的振动。

图1 导管三维模型Fig.1 3D Model of Tube

简谐激励力作用下，在导管根部形成对称循环应力是造成导管根部疲劳的因素之一。蓄压器导管在空间3 个方向可简化为单自由度线性强迫振动，见图2。

图2 单自由度导管简化模型Fig.2 Simplified Model of Single Degree Freedom Tube

导管x、y、z3 个方向的单自由度线性强迫振动运动微分方程为

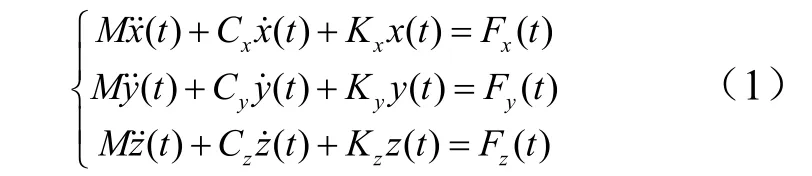
式中M为导管质量；Cx，Cy，Cz，Kx，Ky，Kz，Fx，Fy，Fz分别为导管在x、y、z3 个方向的阻尼系数、刚度系数及受到的力。

液压泵工作时产生的脉动压力作用在导管壁上形成激励力，可表示为

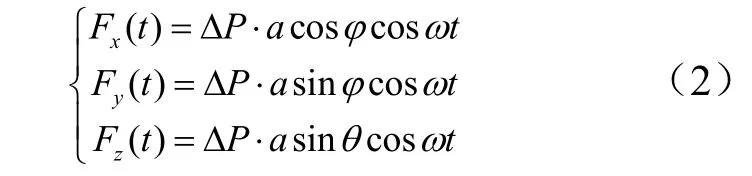
式中 ΔP为液压脉动压力幅值；a为脉动压力作用面积；φ，θ分别为脉动压力作用方向与x、y方向夹角；ω为脉动频率。

导管x、y、z3 个方向的位移响应幅值为

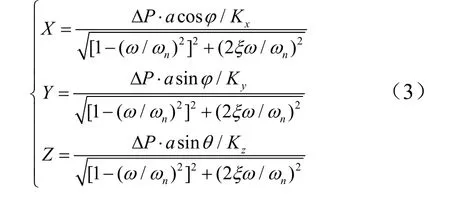
式中ωn为导管自然频率，为导管阻尼比，

导管根部最大应力可依据悬臂梁挠曲理论推导：

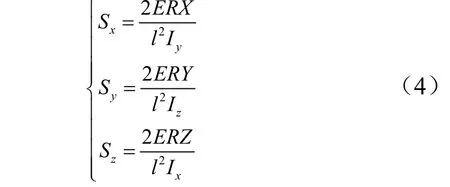
式中E为材料弹性模量；R为导管外径；l为导管重心与根部的距离；Ix，Iy，Iz分别为导管对x、y、z3 个方向的惯性矩。

导管振动模型可作为导管疲劳失效分析的理论依据，指导导管振动疲劳分析及后续设计改进。然而伺服机构蓄压器导管振动特性同时受焊缝、蓄压器壳体等因素影响，结合有限元仿真进行分析，可得到更为理想的结果。

2 导管疲劳强度理论

为评估导管疲劳强度，需建立外载荷与材料寿命之间的关系，即S-N曲线。采用幂指数公式对材料的S-N曲线进行拟合：

式中S为对称循环应力；N为循环次数；α，Ct为材料常数。

蓄压器导管材料为TA18（Ti-3Al-2.5V），取焊接区域材料参数为基体材料的 0.8 倍，拟合可得当N≤ 106，α= 19.55,Ct= 9.33 ×1 054；当N＞ 106，α= 72.52，Ct= 4.79 × 1 0187，S-N曲线如图3 所示。

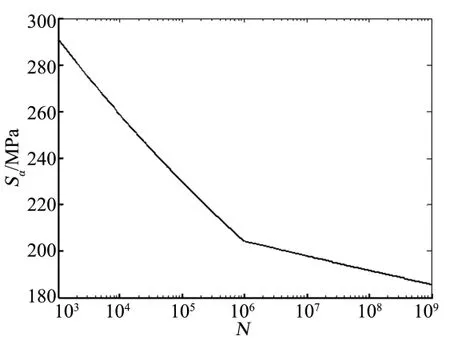
图3 导管焊接区域材料S-N 曲线Fig.3 S-N Curve of Tube Welding Area Material

导管通过焊接与蓄压器壳体固接，焊接部位存在焊接残余应力。此外还存在导管内油液工作压力产生的应力，相当于在导管根部叠加一个偏置静应力，即非对称循环中的平均应力，与压力脉动叠加作用在导管根部。非对称循环应力采用Goodman 直线模型修正，见式（6）。

式中S-1为对称循环疲劳极限Sm=Sp+Sc，为平均应力；Sp=P·r/(R-r)为工作压力产生的应力，其中P为工作压力，R，r分别为导管外径和内径；Sc为焊接残余应力；σb为材料抗拉强度。

3 仿真与试验

导管规格为Φ8×1 mm，长度为150 mm，弯曲半径为15 mm，材料为钛合金TA18（Ti-3Al-2.5V），材料属性如表1 所示。

表1 导管材料属性Tab.1 Property of Tube Materals

导管根部焊接在蓄压器壳体上，焊缝高度3 mm，蓄压器导管有限元模型如图4 所示。

图4 蓄压器导管有限元模型Fig.4 Finit Element Model of Accumulator Tube

伺服机构工作压力P=21 MPa，考虑液体附加质量，对蓄压器导管进行模态分析，获得蓄压器导管自然频率为1826 Hz，模态分析结果如图5 所示。施加工作压力后，导管根部最大应力为83.6 MPa。

图5 蓄压器导管模态仿真结果Fig.5 Modal Simulation Result of Accumulator Tube

伺服机构工作时，压力脉动沿导管入口方向施加谐波激振力，液压脉动压力幅值ΔP=0.25 MPa，压力作用面积a=28.26 mm2，柱塞泵转速12 000 r/min，柱塞数9 个，计算可得柱塞泵压力脉动激振频率f=1800 Hz。施加谐波激励力后的导管根部等效应力为60 MPa，如图6 所示。

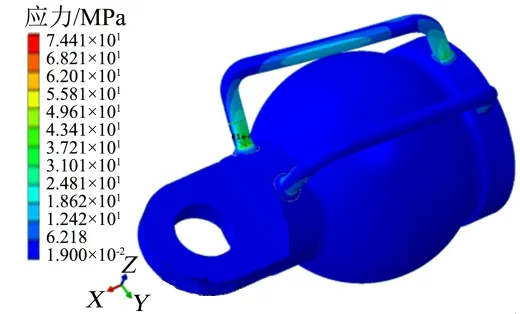
图6 施加压力脉动后蓄压器导管仿真结果Fig.6 Simulation Result of Loading Pressure Pulse for Tube

计算结果表明，蓄压器导管在工作压力和脉动压力共同作用下，根部受到弯曲应力为146.3 MPa，对应疲劳寿命为5.76×1051。可见，工作压力与脉动压力共同作用下，导管在有限工作次数（108）内不会发生疲劳失效。

焊接残余应力对导管根部疲劳强度有不可忽略的影响，一般采用X 射线应力测定的方法获取。在分析工作中，根据故障导管的工作时间（疲劳寿命）、工作压力导致的应力（工作应力）和脉动压力导致的应力（脉动应力），利用疲劳寿命模型与Goodman 修正模型，可计算得到残余应力为213.7 MPa，如表2 所示。进一步分析，不妨预设导管焊接残余应力为113.7 MPa，在工作压力与脉动压力作用下，施加预设残余应力，采用Goodman 模型计算等效应力，代入导管疲劳强度模型中可得疲劳寿命，计算结果见表2。

表2 考虑残余应力的导管疲劳强度计算值Tab.2 Fatigue Life of Loading Residual Stress for Tube

从计算结果中可得，工作应力与脉动应力不变的情况下，残余应力分别为213.7 MPa 和113.7 MPa 时，对应疲劳寿命5.02×107和2.99×1026，表明残余应力是造成导管疲劳失效的重要因素。

针对残余应力对疲劳裂纹的影响，采用X 射线应力测定的方法，对某伺服机构失效导管相同批次31 件次导管根部进行了残余应力测量（如图7 所示）。测量结果表明，最大拉应力为275.8 MPa，最大压应力为-197.1 MPa，且沿导管轴向应力梯度变化较大。仿真与实际测量结果均表明，压力脉动谐波激励与残余应力共同作用，造成导管根部疲劳失效。

图7 蓄压器导管残余应力测量Fig.7 Welding Residual Stress Testing of Accumulator Tube

依据研究成果，改进措施为合理设计导管，长度尺寸由145～155 mm 增加到170～175 mm；改进残余应力去除工艺，焊接后时效温度由500～510 ℃提高到640～650 ℃。改进后，导管固有频率由1641～1922 Hz降低到1203～1268 Hz。最大残余拉应力由275.8 MPa降低到48 MPa。新批次导管随伺服机构通过高频随机振动、50 h 寿命试验考核，并通过了飞行试验考核。