螺栓法兰连接结构的拉压不同刚度动力学模型

栾 宇，关振群，程耿东，阳志光，冯韶伟

（1.北京宇航系统工程研究所，北京，100076；2.工业装备结构分析国家重点实验室，大连，116023）

0 引 言

螺栓法兰连接结构是一种典型的结构连接形式，广泛应用于航天器等工业结构中。但是，连接本身破坏了结构的连续性，在连接面（对接面）引入了接触与摩擦、甚至碰撞等非线性因素，这就使得螺栓法兰连接结构的动力学特性较为复杂，不易分析[1]。

连接结构的静力分析一般通过基于有限元的接触算法实现，但限于动力学算法、动力学建模技术、碰撞—摩擦与耗散以及计算成本等因素，螺栓法兰结构的动力学计算还没有形成统一的范式[2]。

传统上，为了计算运载火箭、导弹等结构的整体动力学特性及动力响应，首先建立简化线性梁模型，结合试验模态方法进行动刚度修正与模型确认[3]，然后将动力学外载加载在模型上，以获取截面的内力响应数据（弯矩、剪力、轴力）作为结构设计中的载荷依据[4]。线性梁模型中法兰的连接刚度通常被等效为梁的弯曲刚度或扭矩弹簧的扭转刚度[5]。但是，法兰连接结构实际上是接触非线性问题，即连接刚度取决于连接面的状态[6]，因此，线性模型无法准确描述其力学特性。

本文首先对典型螺栓法兰连接结构的静力特性进行了研究，阐明了其轴向拉压不同刚度这一重要特性；然后，在连接结构的动力学简化建模中引入了双线性弹簧模拟其拉压不同刚度特性。为研究冲击响应机理，本文将螺栓法兰连接结构抽象为两自由度的质量-弹簧系统，对系统的冲击响应进行了理论分析，并开发自适应递归算法进行动力学数值求解。

1 螺栓法兰连接结构静力响应特性

为了研究螺栓法兰连接结构的力学特性，选取典型的螺栓法兰连接结构（见图1）进行静力分析。选取结构由两段相对连接面完全对称的柱壳结构组成，柱壳材料为Q235 结构钢；两段柱壳之间由外翻法兰和4颗M10 螺栓进行连接，螺栓材料为S45 合金钢。

图1 典型螺栓法兰连接结构Fig.1 Typical Bolted Flange Connection

静力分析通过有限元软件ANSYS 实现，在一端固支的条件下，在自由端对结构施加轴向拉压荷载与弯矩，分析考虑了连接面的接触与摩擦（摩擦系数0.2）。

1.1 轴向载荷下的变形响应

由连接结构的轴向拉压载荷-位移曲线（见图2），螺栓法兰连接结构在轴向表现出明显的拉压刚度不同特性，这是其连接刚度非线性的重要体现。

图2 轴向位移-载荷曲线Fig.2 Curve of Axial Displacement and Load

研究表明，螺栓法兰连接结构的轴向拉压不同刚度是由连接面的接触状态及连接区域的传力路径在拉压荷载作用下不同造成的[8]。

1.2 弯矩下的变形响应

在弯矩作用下，螺栓法兰连接结构不仅产生了弯曲变形，还产生了轴向变形（如图3 所示），即横向荷载可引起横向与轴向耦合变形，这是螺栓法兰连接结构的另一重要特性。

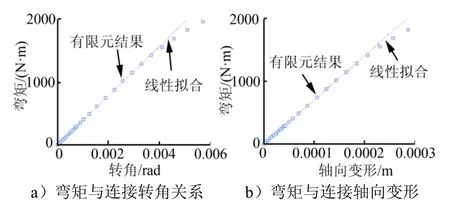
图3 弯矩作用下连接结构位移曲线Fig.3 Curve of Axial Displacement and Load

产生这种响应特性的原因为受拉侧与受压侧的刚度不同，即轴向拉压刚度不同，从而使得在弯矩的作用下受压和受拉产生了不同数值的轴向位移所致[7]。

综上所述，螺栓法兰连接结构在轴向存在显著的拉压刚度不同特性。在横向载荷作用下，轴向刚度拉压不同特性又导致连接面同时产生轴向和横向变形响应。

2 螺栓法兰连接结构动力学建模

2.1 将螺栓法兰连接结构等效为转角弹簧

2.1.1 将连接结构等效为转角弹簧

使用线型方法对连接结构进行建模，如图4 所示。

图4 单自由度线性模型Fig.4 Linear Model for One DOF

只考虑弯矩引起的转角变形θ，而不考虑轴向变形（见图4b），这样就可将连接结构等效为一转角弹簧。转角弹簧连接面的转动刚度可表述为

式中M为作用于连接面的弯矩；θ为连接面的转角。

建立线型梁模型，将被连接结构简化为梁单元，在两段梁单元的连接处建立独立重节点，并用转角弹簧单元连接两重节点，对两节点间除相对转动外的其他自由度进行耦合（见图4c）。

2.1.2 动力学响应

将与连接结构相连的部段简化为相应的转动惯量J，并对连接刚度kM的弹性部分进行线性拟合，如图5所示。

图5 弯曲刚度Fig.5 Curve of Axial Displacement and Load

连接面的无阻尼振动方程可表示为

通过待定系数法，可解得连接结构在初始条件（θ(0)=θ0，）的动力学响应为

式中ωθ为连接结构的转动频率，。

由式（2）及式（3）可知，线性建模的实质是将螺栓连接转化为转角弹簧的一维问题，动力响应中只有转动响应，并无轴向响应。

2.2 螺栓法兰连接结构的拉压不同动力学模型

2.2.1 拉压刚度不同弹簧的引入

通过第1.1 节的讨论，螺栓法兰连接结构的一个重要特性是轴向拉压不同刚度。为了模拟连接结构轴向的拉压刚度不同特性，这里引入用拉压刚度不同的单轴弹簧单对连接段进行建模，弹簧拉压曲线如图6 所示。

图6 弹簧拉压曲线Fig.6 Curve of Axial Displacement and Load

弹簧的刚度可由拉伸刚度k+和压缩刚度k-确定，其数值可由有限元分析或静力试验获取。

弹簧刚度可写为

式中 上标“*”表示弹簧的刚度实际取决于弹簧的拉压状态；δ表示弹簧的变形，受拉为正，受压为负。

引入符号函数sgn(δ)，k*可表示为

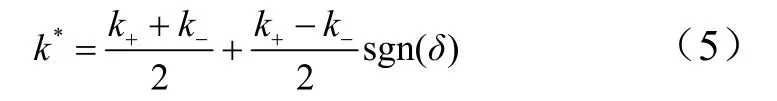
2.2.2 理论模型的建立

在建模过程中，同样将连接结构等效为梁单元；对于连接结构，使用刚性梁单元（位移偶和约束）来模拟连接面，刚性梁的中点与梁单元相连，两端与双线性弹簧单元相连，如图7 所示，其中δ1和δ2为两弹簧的轴向变形，b为连接结构宽度。这样，就可在准确模拟弯曲刚度的同时，在轴向准确模拟拉压刚度不同。

图7 含有拉压不同弹簧的非线性模型Fig.7 Model with Bilinear Springs

2.2.3 动力学响应研究

为研究螺栓法兰连接的动力响应，进一步将模型简化为1 个两自由度的质量-弹簧系统，如图8 所示。

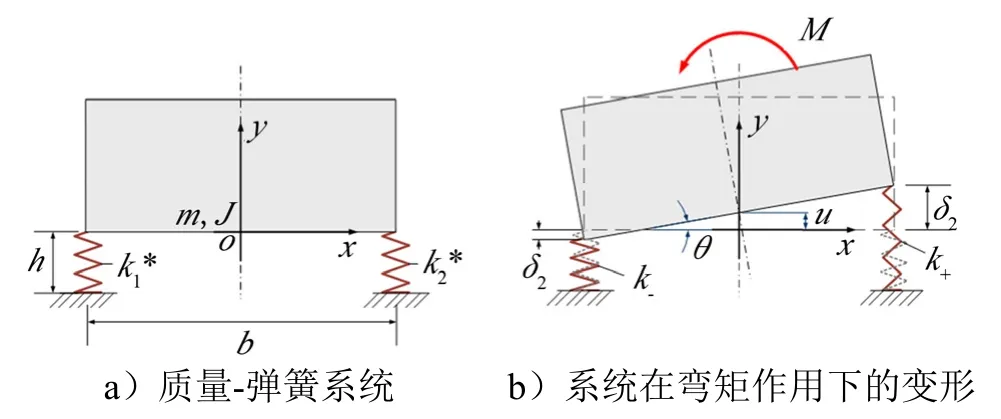
图8 质量弹簧系统Fig.8 Bilinear Model with 2 DOFs

假设整体结构相对于对接面完全对称，仅留取上半部分进行研究。将被连接结构表示为质量m与转动惯量J；连接结构的力学性能由拉压刚度不同弹簧来表述，弹簧只能发生轴向变形，弹簧的下端完全固支，弹簧上端与质量块两端相连。

通过以上简化，将螺栓法兰连接非线性模型抽象为两自由度质量-弹簧模型问题，连接结构的运动可以由连接面中心O的轴向位移u和转角θ描述。

系统的无阻尼自由振动方程为

式中M为质量矩阵；K为刚度矩阵；y为位移向量，y=(u,θ)T；T为质点的动能，可表述为

系统的弹性势能可表述为

式中k1*，k2*为两弹簧的刚度。

由图8b 可知，在弯矩作用下，可获取O点位移与弹簧变形δ1、δ2间的转换关系：

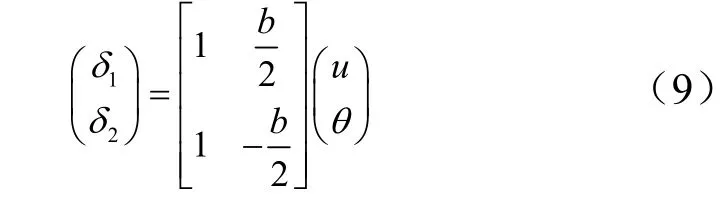
将式（9）代入式（8），系统的弹性势能可进一步写为以(u,θ)为变量的形式：

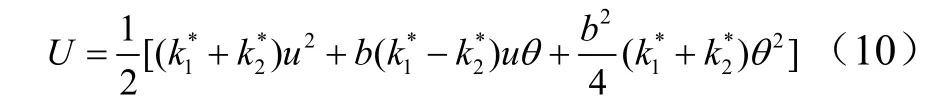
最后，将式（7）、式（10）代入拉格朗日方程，即可得到系统的无阻尼自由振动方程：

其中，

由式（11）可知，只需确定刚度矩阵，即确定k1*与k2*，就可在给定的初始条件下定解。将式（9）代入式（5），弹簧刚度可表示为(u,θ)的函数：

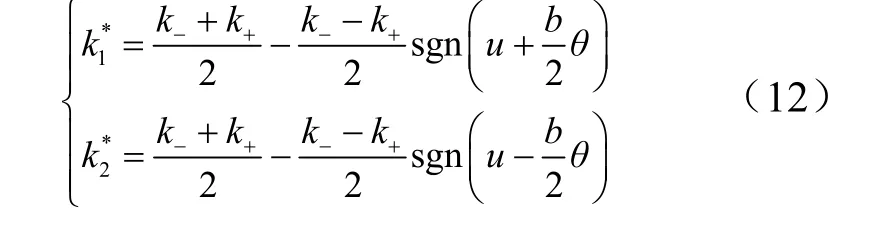
通过以上的讨论发现：系统刚度矩阵的取值实际取决于弹簧的拉压状态。若以弹簧变形为0 作为分界，质点的运动可在运动平面上划分为4 个区域（见图9），每个区域含有独立的、与其他区域不同的弹簧拉压状态组合。这样就把系统的运动根据运动区域划分为4种情况，并可逐一确定各区域的刚度矩阵，进而求得各区域的频率与振型。

图9 运动分区Fig.9 Divisions of Vibration

由图9，在II、IV 运动分区，刚度阵存在耦合项，这表明存在发生u、θ耦合振动，由于u、θ分别代表纵向横向位移，因此这里将这种现象称为横纵耦合振动。横、纵耦合振动产生的根本原因是拉压刚度不同。当拉压刚度相同时（I、III 分区），耦合项变为零，不会出现横纵振动之间的耦合。

设系统的控制方程（式（11））的解为

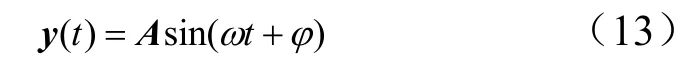
式中A和φ分别为响应的振幅与相角。将初初始条件带入运动方程即可确定系统在各区域的振动响应。

3 横向冲击荷载作用下的动力响应计算

3.1 计算说明

3.1.1 非线性模型数值计算

根据动量定理，将横向冲击荷载等效为一初始转角速度。这样，系统的初始条件可表示为

对于拉压不同问题的求解，困难在于如何有效地确定弹簧恢复到平衡位置的时刻，即弹簧拉压状态的转换时刻。若直接使用积分法对控制方程（式（11））进行求解，将导致在跨区时产生能量损耗，从而降低求解的精度，而利用光滑函数对刚度曲线进行拟合并不适合阶跃函数的求解[9]。

为了确定跨区时刻（弹簧过零检查）并同时减少跨区时系统能量的损失，本文应用递归算法，使用二分法对跨区时刻进行捕捉，以获取系统在计算时长T内任意精度ε下的跨区时刻。

非线性模型计算流程计算流程如图10 所示，其中t为计算时长，t0为分区内计算时长，i(t)为t时刻运动所在分区（i=1～4），y(t)为系统状态，Dt为初始输入步长预定义步长，数值计算使用C 语言实现。

图10 计算流程Fig.10 Program for Solution

非线性计算时长为T=2 s，计算规定步长为Dt=1×10-3s，ε=1×10-15s，初始转角速度为θ(0)=0.5 rad/s，非线性模型计算其他参数如表1 所示。

表1 拉亚不同刚度模型计算参数Tab.1 Parameters for Bilinear Model

为方便建立响应的线性模型，这里使用快速傅里叶变换对计算结果的进行了分析，系统的转动振动响应基频为fθ=5.6 Hz，轴向振动响应基频为fu=11.2 Hz。

3.1.2 线性模型数值计算

为了建立与非线性模型频率相等的线性模型，在已知非线性模型响应频率fθ的条件下，转角弹簧的弯曲刚度可按式（17）计算，再代入式（3）即可直接求取模型的响应：

其中，ωθ=2πfθ。数值解由式（3）差值而得，插值间隔Δt=1×10-3s，时长为2 s，计算参数如表2 所示。

表2 单自由度线性模型计算参数Tab.2 Parameters for Linear Model

3.2 计算结果比较

3.2.1 位移响应比较

图11、图12 分别为转角、轴向位移的时程响应，在横向弯矩冲击的作用下，拉压不同模型同时产生了等量级的轴向与横向振动；拉压相同线性模型只产生了转动位移响应。

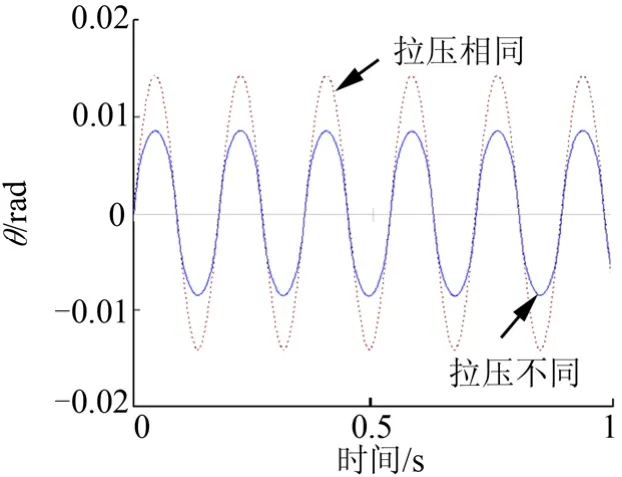
图11 转角时程响应Fig.11 Respond of Rotational Displacement

图12 轴向位移时程响应Fig.12 Respond of Axial Displacement

3.2.2 内力响应比较

在拉压不同弹簧模型中，若有k+=k-=，即弹簧的拉压刚度相同时，则拉压不同弹簧模型可等效为线性模型；换言之，若将第2.1 节中的线性模型等效为与图8 相同的轴向质量-弹簧系统，转角弹簧的刚度转化为两轴向拉压刚度相同的弹簧即可，其等效关系可表示为

代入第3.1.2 节中求得的kM，可得对应的等效拉压弹簧刚度=1.55×106N/m。接着，将求得的扭转弹簧时程响应代入式（9），即可得与其等效的轴向弹簧的轴向变形，如图13 所示。

图13 弹簧变形时程响应Fig.13 Deformation of Springs

对于线性模型，等效弹簧内力响应可按下式计算：

拉压不同弹簧模型的弹簧内力响应根据弹簧的变形响应按下式计算：

通过对比图13、图14 结果可知，转动初速度为0.5 rad/s 时，拉压不同模型中弹簧最大伸长为0.024 m，转角最大值为0.008 53 rad，最大弹簧拉力为24 kN；线性模型等效弹簧最大伸长为0.014 m，转角最大值为0.014 03 rad，等效弹簧最大拉力为22 kN。以弹簧最大拉力进行比较，拉压不同模型结果比传统线性模型结果要高出9%，也就是说，传统模型获得的荷载结果可能偏小。

图14 弹簧力时程响应Fig.14 Spring Force for Both Model

4 结束语

本文对典型螺栓法兰连接结构的静力响应进行分析发现，在轴向荷载作用下，螺栓法兰连接结构具有明显的拉压不同刚度特性；使得其在弯曲荷载的作用下，产生了转角变形的同时产生了轴向变形，这是螺栓法兰连接结构的另一重要特性。

通过引入拉压刚度不同弹簧对连接结构进行简化建模，不但可以准确的模拟结构轴向的拉压不同刚度特性，还可以模拟弯矩作用下连接结构产生的轴向变形。理论分析与数值模拟均表明，拉压不同刚度非线性动力学模型在横向荷载作用下将发生横纵耦合振动现象。在相同的横向冲击荷载作用下，拉压不同刚度非线性动力学模型产生了比传统模型更大的变形以及截面内力响应，也就是说，传统模型获得的荷载结果可能偏小。本研究对于提高螺栓法兰连接结构的安全可靠性具有重要意义。