利率市场化和汇率制度改革有效性研究——基于资产价格交叉和联动效应的实证分析

朱培金

（国家外汇管理局浙江省分局，浙江 杭州 310001）

一、引言与文献综述

有关利率和汇率改革的有效性问题，在国际上引起广泛争论。目前，世界主要经济体均遵循市场化改革路径，充分发挥价格在资源配置中的决定性作用。利率和汇率是金融市场中两个最为重要的价格调节变量，尤其是在利率市场化改革和人民币汇率形成机制改革不断推进的背景下，研究利率和汇率的动态性以及对资产价格的影响，对我国金融市场稳定和金融风险防控具有十分重要的理论和现实意义。

关于利率和汇率两者之间的研究方面，鉴于我国利率和汇率市场化改革持续推进，两者之间的相关性和联动性得到国内学者的高度关注。王春英（2011）通过开放经济的M-F-D 框架，研究中国实际利率与美国实际利率之差和实际有效汇率之间的联动关系，表明中美利率差与实际有效汇率之间存在显著的联动关系。赵胜民等（2013）采用DCC-GARCH 模型研究汇率与利率之间的动态关系，发现两者之间的作用是非线性的，即利率对汇率的影响程度要明显大于汇率对利率的影响程度。陈创练等（2017）基于利率—汇率—资本流动三者传导框架，发现利率传导不顺畅，一方面是我国利率的价格机制有限和资本账户滞后，另一方面是有管理的浮动汇率制度并不能很好反映外汇市场价格，导致“非平抛利率平价”曲线无法更好发挥作用。陈红等（2016）实证分析我国跨境资金流出对经济金融的影响，进而提出为应对跨境资金流出对我国宏观经济的冲击，既要深化汇率制度改革，增强人民币汇率弹性，又要推进利率市场化改革，完善市场机制。

关于利率和汇率对资产价格的传导机制研究方面，主要研究从传导机制的渠道、效应和风险三个层面展开。第一层面是传导机制的渠道问题。钱晓霞（2018）发现，短期跨境资本受利率和汇率波动等影响，具有较强的流动性、投机性和破坏性，会对资产价格造成不利冲击。周姝彤和王春洋（2020）分析汇率市场化改革对国内吸收的作用机制，随着人民币汇率弹性加大，汇率预期对资产价格的影响逐渐减弱，外汇冲击效应减小，有助于宏观经济稳定。第二层面是传导机制的效应研究。罗毅丹和樊琦（2010）研究中国货币政策对通货膨胀与GDP 的冲击效应，发现我国货币政策时变特征明显，且有渐进式的演进机制。全骐（2021）通过货币政策传导机制中市场利率传导的效果和动态变化，证实市场利率传导并未发生“梗阻”。周建和赵静美（2018）采用马尔科夫区制转换计量方法，发现利率转换频次要高于人民币汇率，利率和汇率市场的内生传导机制有待加强。第三层面是价格传导影响宏观经济稳定和金融风险防范。朱培金（2015）发现利率政策对宏观经济稳定时变特征显著，采用时变的分析方法可以较好解释政策变迁的动态影响。

目前，通过利率或汇率单方面对资产价格影响的有效性研究十分丰富，但结合两者的交叉性和联动性对资产价格的影响来分析改革的有效性文献尚不多见。从经济学角度而言，利率政策调节内部均衡，汇率制度调节外部均衡，资产价格受到多种因素影响，面临多种内外部冲击，因此，研究单一因素对其影响必然有失偏颇。随着利率市场化改革和汇率制度改革进入深水区，对资产价格交叉效应和联动效应日益显现，从对价格较为敏感的资产价格分析和衡量利率市场化和汇率制度改革的有效性，成为研究改革有效性的重要手段和检验方式。

二、利率市场化、汇率制度改革以及传导机制研究

为充分发挥价格在资源配置中的决定性作用，本文通过资本市场的反应来检验利率和汇率改革的有效性。从传导机制分析，改革通过价格机制和预期机制两种方式传导至资本市场，从而影响资产价格波动。

（一）价格机制传导

一是利率和汇率传导。根据利率平价理论，在内外部均衡情况下，如果国内利率上升，国外资金流入，打破外汇市场均衡，造成本币升值，此时存在利率（i）与汇率（e）（直接标价法）反向关系，如公式（1）所示。

二是利率与资产价格传导。根据资产价格决定理论，资产价格与利率反向变动，利率越高，资产价格就越低，因此利率（i）与资产价格（Q）呈反向关系，如公式（2）所示。

三是汇率与资产价格传导。因外币不能直接购买本国资产，因此，汇率对资产价格的影响可以分解为两个部分，即利率对资产价格影响与利率对汇率影响的商，由于两者均小于零，它们的商就大于零，如公式（3）所示。

四是利率和汇率交叉因素与资产价格传导。简单分解后，可以发现利率和汇率的交叉因素对资产价格的影响取决于利率对汇率的弹性（εi→e）或汇率对利率的弹性（εe→i）。从利率、汇率弹性看，如果利率对汇率的弹性大于-1（εi→e＞-1），利率和汇率的交叉因素对资产价格影响为负，反之，如果利率对汇率的弹性小于-1（εi→e＜-1），利率和汇率的交叉因素对资产价格影响为正。从汇率、利率弹性看，如果汇率对利率的弹性大于-1（εe→i＞-1），利率和汇率的交叉因素对资产价格影响为正，反之，如果汇率对利率的弹性小于-1（εe→i＜-1），利率和汇率的交叉因素对资产价格影响为负。因此，利率和汇率的交叉因素对资产价格影响表现为不确定性，如公式（4）所示。

（二）预期机制传导

预期是经济主体根据所掌握的信息而选择决策的重要依据。当预期利率上升时，面临跨境资金流入压力，短期内人民币呈升值趋势，表现为汇率下降（直接标价法），而国内利率水平整体上升，导致资产价格下跌，反之亦然。当预期人民币汇率升值时，表现为外币供给过多，在外汇冲销等政策作用下，本币供应量增加，利率趋于下降，导致资产价格上涨，反之亦然。利率和汇率交叉因素影响，因涉及利率和汇率的共同作用，资产价格走势取决于两者的协同作用大小。

实际上，预期机制传导和价格机制传导本质区别在于预期机制的传导更为迅速，可以在利率或汇率尚未开始变化或刚开始变化时，就已经将效应传导到资本市场，如果实际变化大小与市场预期相一致，价格机制作用已经无法对资本市场产生影响，因为影响效应已经提前被资本市场所消化。

三、实证分析

（一）数据及处理

1.利率指标。考虑到数据的长期可获得性，本文选取全国银行间市场拆借利率来衡量利率水平，其中7 天银行间回购利率是中国货币市场上表现最好的基准利率。数据来源于中国人民银行网站，用i表示。

2.汇率指标。本文选取美元兑人民币作为汇率指标（取对数），数据来源于Wind 数据库，用e 表示。同时，本文选取名义有效汇率作为稳健性检验指标（取对数），数据来自国际清算银行，用neer表示。

3.利率和汇率的交叉因素指标。为研究利率和汇率交叉影响对资产价格的影响，用利率和美元兑人民币汇率之间的乘积作为利率与美元兑人民币汇率的交叉因素指标，用i*e表示。同理，用利率和名义有效汇率之间的乘积作为利率与名义有效汇率的交叉因素指标，用i*neer表示。

4.资产价格指标。股票市场和房地产市场作为重要的资产配置场所，其价格受到各种内外部因素影响。本文选取沪深300 指数的月末值（取对数）和全国70个城市房价（取对数）分别作为股市和房市价格的衡量指标，分别用s和h表示。数据来源于Wind数据库。

本文样本区间从2005年7月至2020年4月（见图1）。一方面，人民币汇率改革和全国70 个城市的商品房销售价格指数发布均始于2005 年7 月；另一方面，沪深300 指数发布始于2005 年4 月，可以涵盖大部分流通股，能较好反映市场走势。

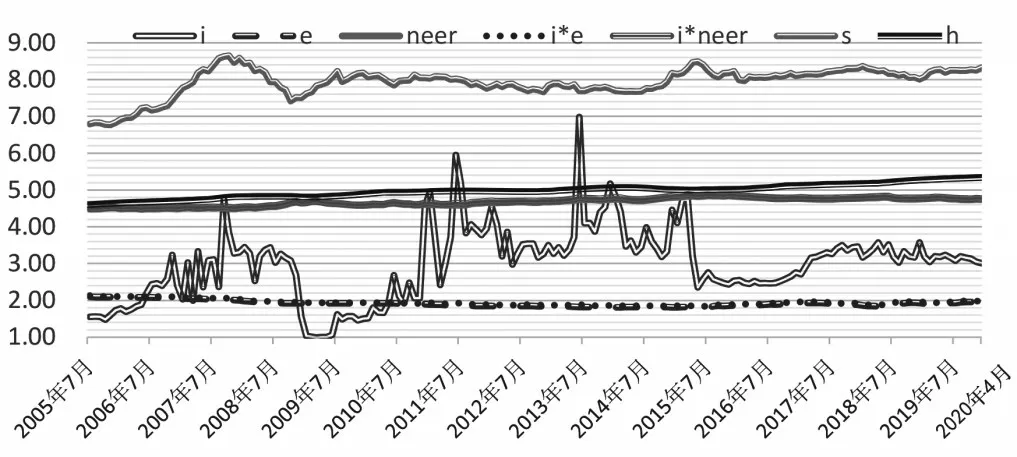
图1 2005年7月至2020年4月各变量走势图

（二）实证检验

1.相关性检验。利率和汇率作为重要的价格指标，它们之间是否具有高度相关性是判别交叉和联动的重要依据。表1展示各变量之间的相关性。

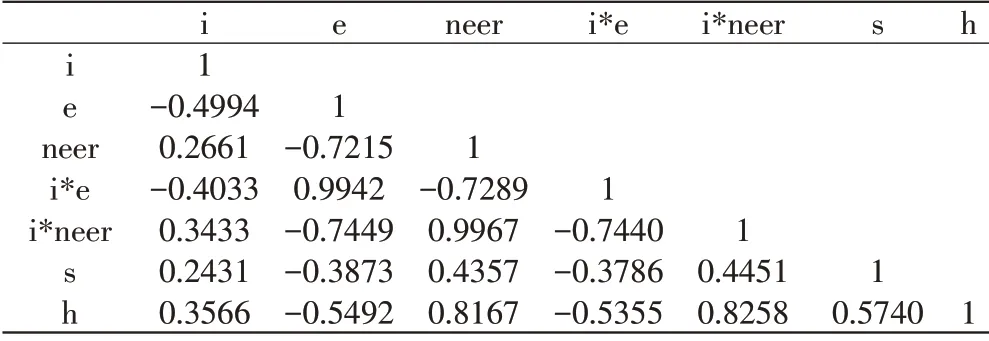
表1 利率、汇率及交叉效应和资产价格之间的相关性分析

从相关性结果看，利率和汇率之间尤其是利率与美元兑人民币汇率之间的相关性较强，呈现负相关特性，相关系数为-0.4994。名义有效汇率、利率和名义有效汇率交叉因素与房价呈现很高的相关性，其相关系数分别为0.8167和0.8258。

2.平稳性检验、格兰杰因果检验和协整检验。本文采用ADF 和PP 两种方法进行平稳性检验，从两种检验结果情况看（见表2），检验结果大致相同。其中，利率（i）在1%的显著性水平下接受平稳性检验；沪深300指数（s）在10%的显著性水平下接受平稳性检验；美元兑人民币汇率（e）、名义有效汇率（neer）、利率和美元兑人民币汇率的交叉指标（i*e）、利率和名义有效汇率的交叉指标（i*neer）未能通过平稳性检验，但一阶差分（d（e）、d（neer）、d（i*e）、d（i*neer））的序列均在1%的显著性水平下接受平稳性检验；商品房销售价格指数（h）在10%的显著性水平下均未通过平稳性检验，但一阶差分（d（h））序列在1%的显著性水平通过平稳性检验。

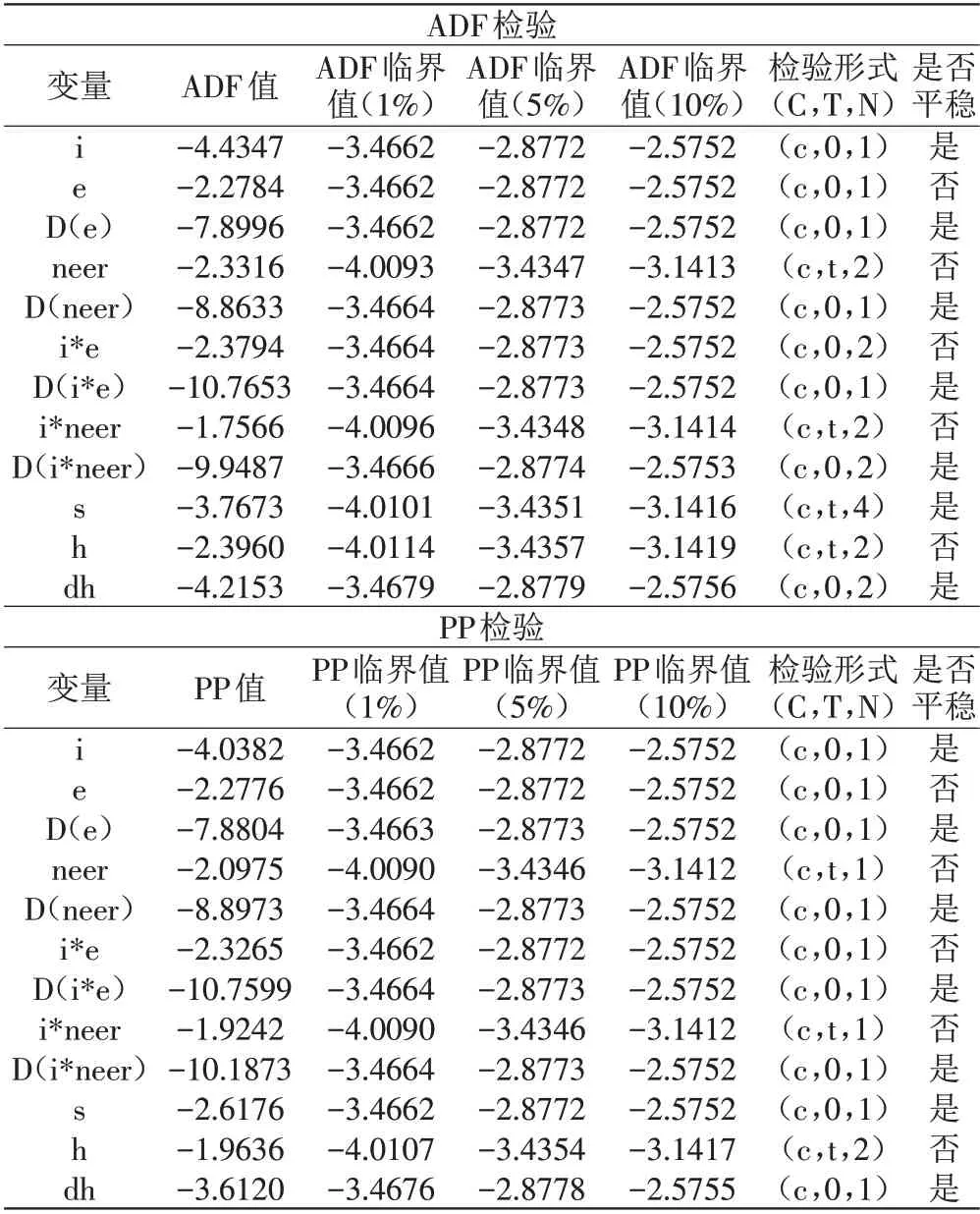
表2 数据平稳性检验结果

在确定变量平稳的基础上，本文通过格兰杰因果检验方法（见表3），从利率与汇率两者看，利率滞后项无法解释美元兑人民币汇率，其P 值为0.1180，相反，美元兑人民币汇率滞后项能在一定程度上解释利率变化，其P 值为0.0836，但利率和名义有效汇率互为格兰杰因果关系，其P 值分别为0.0294 和0.0009。从利率和汇率对资产价格方面看，利率的滞后项能解释房价，名义汇率的滞后项能解释股价和房价，其P值分别为0.0465、0.0241 和0.0185，可以认为利率能引起房价变化，名义有效汇率能引起股价和房价变化。从利率和汇率的交叉因素对资产价格方面看，利率和美元兑人民币汇率的交叉因素是房价的格兰杰原因，利率和名义汇率的交叉因素是股价和房价的格兰杰原因，其P 值分别为0.0000、0.0463、0.0946。与此同时，房价也是利率和名义汇率的交叉因素的格兰杰原因，其P值为0.0270。综上所述，可以发现利率、汇率以及利率和汇率的交叉因素对资产价格具有一定的解释能力，这为构建TVP-VAR模型提供基础。

表3 格兰杰（Granger）因果检验的结果

进一步，本文采用Johansen 方法进行协整检验，迹检验和最大特征根检验均显示，上述变量之间在5%的显著性水平上存在2组协整关系。协整检验结果显示，变量之间存在协整关系，因此实证检验是原序列，而非差分后的序列。

（三）TVP-VAR模型及估计

1.TVP-VAR 模型。VAR模型的一般形式如公式（5）所示。

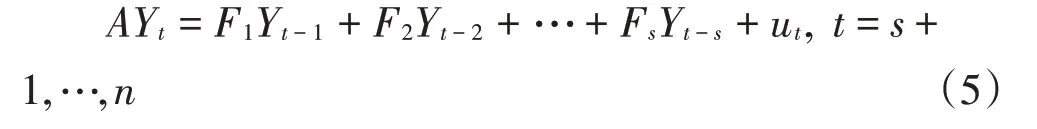
其中，Yt是k×1 维列向量，矩阵A是一个k×k阶下三角，F1,…,Fs是k×k维系数矩阵，ut是k×1 维外生扰动项。因为同步结构冲击A是下三角可逆矩阵，公式（5）左乘A-1得到公式（6）。

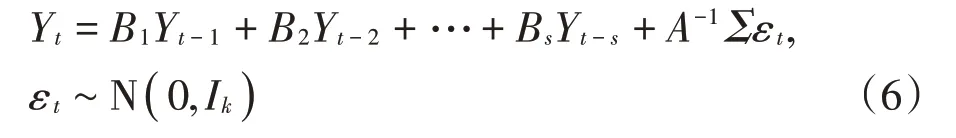
其中，Bi=A-1Fi，i=1,…,s，Σ=diag(σ1,…,σk)，σi是标准差。为简明表达，令Xt=Is⊗(Y′t-1,…,Y′t-s)，⊗是克罗内克积，β是k2s×1 阶系数矩阵，其表达式如公式（7）所示。

如果（7）式满足系数矩阵βt，参数A t和方差矩阵Σt具有时变性，则（7）式可以成为TVP-VAR 模型，其特点在于所有系数具有时变性，能刻画系数的结构变迁，如公式（8）所示。

其中，at=(a21,t,a31,t,a32,t,a41,t,…,ak(k-1),t)′为下三角矩阵A的元素，1,…,k，时变参数服从随机游走，如公式（9）所示。

2.TVP-VAR 模型的估计方法。由于参数具有时变性，TVP-VAR模型参数估计较为复杂，待估参数过多，主要运用贝叶斯推论来进行马尔科夫蒙特卡罗（MCMC）模拟估计。首先设定先验分布，计算出后验分布，采用MCMC 模拟方法进行迭代。简单而言，令，设置先验概率密度π(ω)，在给定数据Y的基础上得出后验分布π(β,a,h,ω|Y)，然后采用MCMC模拟方法进行迭代。

（四）利率、汇率、利率和美元兑人民币汇率交叉因素与资产价格的实证分析

1.TVP-VAR 模型的后验分布。利用OxMetrics 6.0 软件进行估计。为更好计算后验分布，在运用MCMC 方法时，先去掉前2000 次抽样，再进行20000次模拟后的计算结果。

表4 列出贝叶斯估计参数后验分布均值、标准差、95%的置信区间、Geweke收敛诊断值（CD）和无效影响因子（Inefficiency）。其中，Geweke 收敛诊断值（CD）是检验马尔科夫的集中度指标，无效影响因子（Inefficiency）是计算衡量MCMC混合链的指标。图2给出经过MCMC模拟后的参数分布情况。

表4 参数贝叶斯估计值后验分布表

图2 MCMC模拟的参数分布情况

2.等间隔脉冲响应函数。TVP-VAR是多元时间序列模型，部分系数和冲击的协方差矩阵具有时变性，故能捕捉到参数的时变性和可能存在的非线性特征。等间隔脉冲响应函数是在给定时间间隔下，每期自变量单位冲击在固定时间间隔中的对应变量脉冲响应函数图。图3是TVP-VAR模型的等间隔脉冲响应函数图，实线、长虚线、短虚线分别代表滞后半年、一年和两年的脉冲响应。

图3 等间隔脉冲响应函数

第一，利率冲击的脉冲响应。从实证分析看，利率冲击对自身、汇率以及资产价格影响较大。首先，利率冲击对自身影响较大，利率冲击提高对未来利率水平有负向冲击效应，而且在2014 年前后有一个较大的峰值。其次，利率冲击对汇率先有一个正向冲击，此后冲击效应会减弱，经过短暂的负效应后，又会形成一个持续的正向冲击。再次，利率冲击对利率和美元兑人民币汇率的交叉因素具有长期性。另外，利率冲击会造成股价短期的正向效应，此后经过一定时期的减弱后，又会形成第二波正向效应。最后，利率冲击对房价有负面效应，在2012 年前后效应由负转为正，后又急剧下降。

第二，汇率改革冲击的脉冲响应。首先，汇率冲击对利率影响较大，一个正向的汇率冲击会造成利率类似正弦函数的波动。其次，汇率冲击对自身、利率和美元兑人民币汇率交叉因素、股价的影响具有短暂的波动性。最后，汇率冲击对房价影响较为显著，波动剧烈。

第三，利率和美元兑人民币汇率交叉因素冲击的脉冲响应。利率和汇率的交叉因素冲击对利率及房价影响较大，但对汇率、利率和汇率交叉因素、股价的影响较小。

3.时点脉冲响应函数。时点脉冲响应函数是在每一时点对VAR 模型进行估计，动态刻画模型的结构变化。图4 是时点脉冲响应函数图，其中实线、叉虚线、三角虚线分别代表40期、80期和110期的模型方差刻画冲击响应函数。利率冲击对利率自身、汇率、汇率交叉因素存在先瞬时上升，此后逐步回落的过程，但40 期的冲击对股价形成先下降后逐渐上升至0的过程，80期和110期的冲击对股价是先上升后逐渐回落的过程，40期和110期的冲击对房价是先下降后逐渐上升至0的过程，80期的冲击对房价是先上升后逐渐回落的过程。汇率冲击对各变量的影响基本都是先上升后逐步回落的过程。利率和美元兑人民币汇率冲击对各变量的影响也遵循先上升后逐步回落的过程。

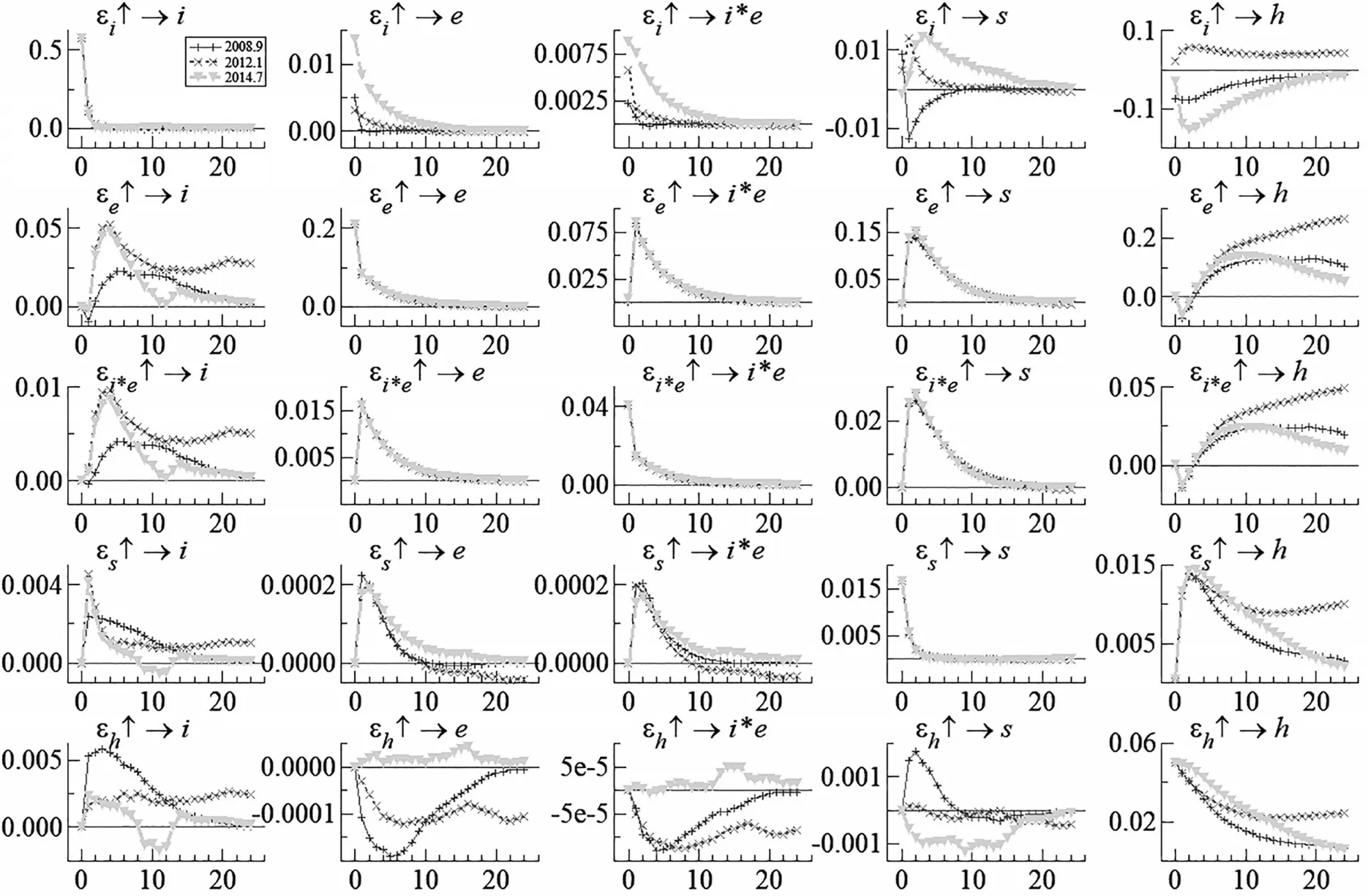
图4 时点脉冲响应函数

（五）稳健性检验

本文采用名义有效汇率替代人民币兑美元汇率，对利率、名义有效汇率、利率与名义有效汇率交叉因素对资产价格的影响进行检验，稳健性检验侧重于时变方差和脉冲响应函数的具体结果。

1.等间隔脉冲响应函数。图5 是TVP-VAR 模型的等间隔脉冲响应函数图，实线、长虚线、短虚线分别代表滞后半年、一年和两年的脉冲响应。

图5 等间隔脉冲响应函数

第一，利率冲击的脉冲响应。从实证分析看，利率冲击对自身、汇率以及资产价格影响较大。首先，利率冲击对自身影响较大，利率冲击提高对未来利率水平有负向冲击效应，且在2014 年前后有一个较大的峰值。其次，利率对汇率、利率和汇率交叉因素、股价形成一个在0 刻度附近剧烈波动的长期影响。最后，利率冲击对房价具有负面效应，在2012年前后效应由负转为正，后又急剧下降。

第二，汇率改革冲击的脉冲响应。首先，汇率冲击对利率影响较大，一个正向的汇率冲击会造成利率出现持续波动，主要是因为名义有效汇率与美元兑人民币汇率的表示方式不同，名义有效汇率采用间接标价法，数值越大则表示人民币升值幅度越大，而美元兑人民币汇率采用直接标价法，数值越大表示人民币贬值幅度越大，因此名义汇率的冲击与图3 刚好相反。其次，汇率冲击对自身、利率和名义有效汇率交叉因素、股价的影响有短暂的波动。最后，汇率冲击对房价影响存在一个较为显著的负面效应，波动剧烈。基于汇率的标价法不同，冲击房价的效应与图3刚好相反。

第三，利率和名义有效汇率交叉因素冲击的脉冲响应。利率和汇率的交叉因素冲击对利率以及房价影响较大，但对汇率、利率和汇率交叉因素、股价的影响较为平稳，而且作用效果刚好与图3相反。

2.时点脉冲响应函数。图6 是时点脉冲响应函数图，其中实线、叉虚线、三角虚线分别代表40期、80期和110 期的模型方差刻画冲击响应函数。利率冲击对利率自身有先瞬时上升后逐步回落的过程，利率冲击对汇率、汇率交叉因素、股价有先下降后逐步上升至0的过程，但40期和110期的冲击对房价是先下降后逐步回归至0的过程，80期的冲击对房价是先上升后逐渐回落的过程。名义有效汇率冲击对利率、名义有效汇率、利率和名义有效汇率交叉因素的影响呈先上升后逐步回落的过程，但对房价的影响是先下降后逐步上升至0 的过程。利率和名义有效汇率冲击对利率、名义有效汇率、利率和名义有效汇率交叉因素的影响呈先上升后逐步回落的过程，但对房价的影响是先下降后逐步上升至0的过程。

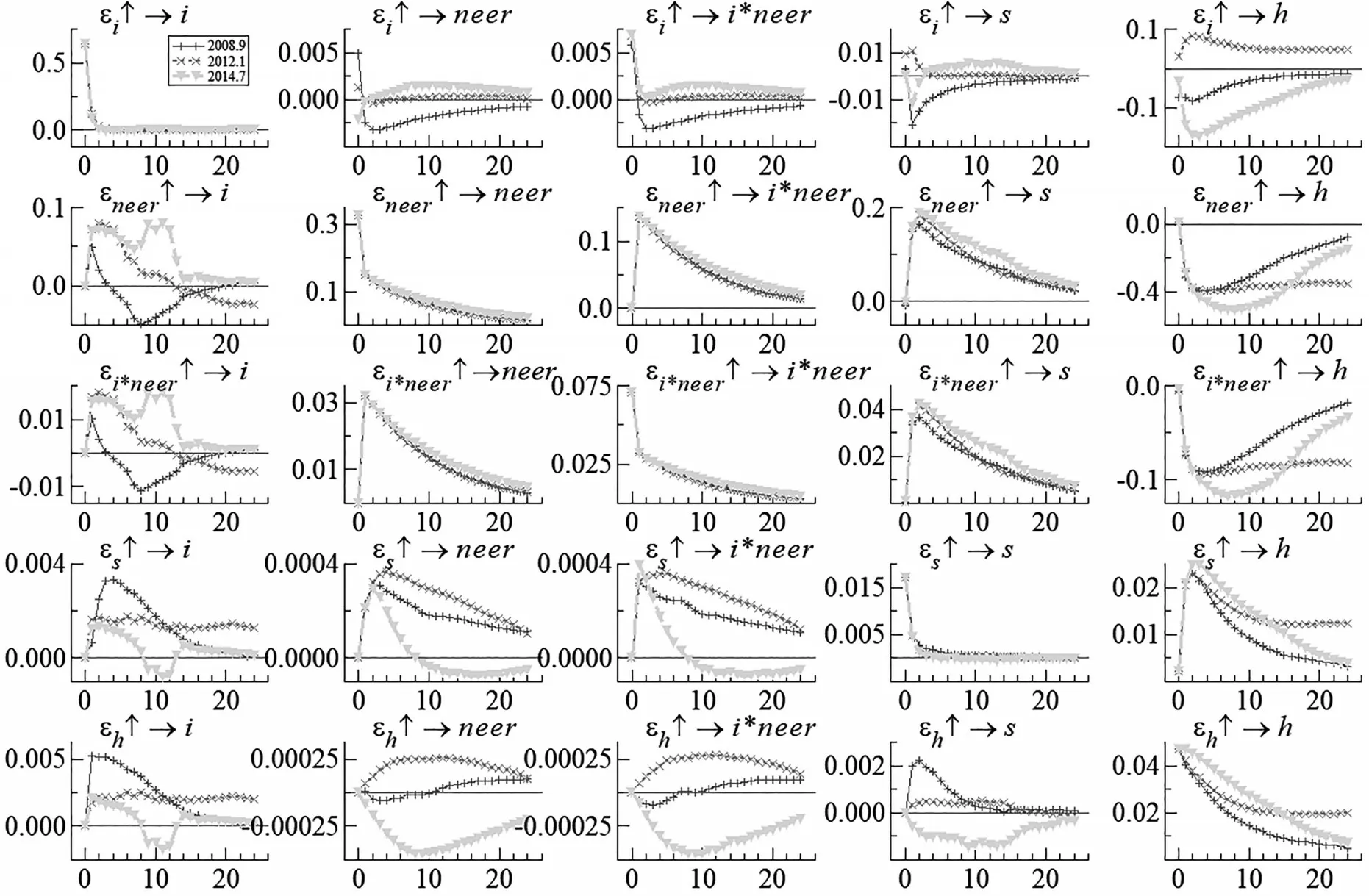
图6 时点脉冲响应函数

综上所述，除名义有效汇率和美元兑人民币汇率在冲击影响的方向上存在差别外，其他效应在作用方式上均表现出高度相似性，表明模型具有较高的稳健特征。

四、结论

鉴于改革的持续性和时变性特征，利用2005年7月至2020年4月时间序列数据，采用具有时变特征的TVP-VAR模型，分析利率市场化、汇率制度改革与资产价格的联动性和交叉性。总体而言，利率、汇率、利率和汇率改革的有效性有所提升。主要结论有以下几方面。

一是利率和汇率的时变性。这种时变性能在一定程度上反映出利率和汇率改革的有效性，尤其是利率对股价、利率对房价的随机变量方差出现较大波动。

二是利率对资产价格的影响。从等间隔脉冲响应函数看，滞后期不同导致等间隔脉冲响应大小不同，如滞后期越大，利率对资产价格的影响越小，但影响走势高度一致，即利率上升，引起股价和房价下降。从时点脉冲相应函数看，不同时点利率冲击对资产价格的影响表现较为复杂。具体而言，2008 年利率对股价和房价的影响为负；2012 年利率对股价的影响为正，但对房价的影响为负；2014年后利率对股价和房价的影响均为正。这种正负交错的影响结果间接证明我国股市和房市对利率传导机制仍有“梗阻”。

三是汇率对资产价格的影响。从间隔脉冲函数看，汇率对不同资产价格的作用并不相同，对股价影响较为温和。从短期看，一个百分点的冲击将造成股价上涨0.075个百分点，长期（两年）来看，作用效果几乎为零；对房价的作用较为显著且波动性较大。从时点脉冲函数看，汇率对股价的影响并不随时间点的不同有所变化，因为三条不同时间点的脉冲图几乎重合，而汇率冲击对房价的影响可能存在某种发散作用，导致汇率提高，即人民币贬值可能引起房价的持续上涨。

四是利率和汇率交叉因素对价格的影响。利率和汇率的交叉因素对资产价格的影响与汇率对资产价格的影响表现为高度一致，其主要原因在于利率是一组平稳序列，两者的乘积与汇率走势高度趋同，从而表现出汇率类同的作用机制。