不同轴偏转对中、 下承式拱桥吊杆承载能力的影响
2021-08-20邓年春周一鸣
邓年春, 周一鸣
(广西大学 a.土木建筑工程学院; b.广西防灾减灾与工程安全重点实验室;c.工程防灾与结构安全教育部重点实验室, 南宁 530004)
在中、 下承式拱桥中, 桥面系主要通过吊杆与拱肋连接。吊杆沿桥梁纵向均匀排列, 将桥面系所受荷载均匀传至拱肋, 这种桥梁结构长期以来被认为是安全可靠的[1]。然而近几十年来, 发生了大量拱桥吊杆断裂事故, 例如美国希尔福桥、 四川宜宾金沙江南门大桥(图1)、 新疆库尔勒市郊的孔雀河大桥、 福建公馆大桥以及台湾南方澳跨海大桥, 事故调查表明, 这些吊杆断裂事故是由吊杆中的钢绞线或平行钢丝突然断裂导致的[2-6]。相关学者提出了可能导致吊杆突然断裂的原因, 例如吊杆的疲劳和腐蚀[7-10]。然而, 斜拉桥和悬索桥中的斜拉索和吊杆也会受到疲劳和腐蚀的作用, 但斜拉桥和悬索桥中并未出现频繁的桥梁拉索断裂事故。因此, 中、 下承式拱桥存在特有的导致吊杆频繁断裂的因素。
在温度作用下, 桥梁结构将产生温度变形。 对于中、 下承式拱桥, 其拱肋被两端基础约束, 无法产生纵桥向的温度变形; 但对于桥面系, 由于桥梁伸缩缝的存在, 桥面系沿纵桥向可以产生温度变形。 拱肋和桥面系之间的变形差将导致连接两者的吊杆发生不同轴偏转(图2)。类似的弯曲变形也存在于斜拉桥和悬索桥的斜拉索和吊杆中, 但由于斜拉索在斜拉桥中未垂直布置, 拉索两端位移主要引起斜拉索索力的变化, 拉索的弯曲变形可以忽略不计[7, 10]; 在悬索桥中, 主缆采用柔性结构, 刚度较小, 无法使吊杆发生弯曲变形。综上, 对于中、 下承式拱桥, 由温度引起的吊杆不同轴偏转是其独特现象, 并可能是导致吊杆承载力不足, 而发生断裂的一项重要因素。

图2吊杆的不同轴偏转
因此, 本文对中、 下承式拱桥吊杆在不同轴偏转下的承载力进行了研究。通过有限元分析和试验对吊杆的偏转角度、 下锚固区最大弯曲应力和钢绞线偏转时的力学性能等(主要研究由钢绞线组成的吊杆)影响吊杆承载力的重要因素进行了量化研究, 提出了吊杆在不同轴偏转下的承载力校核方式, 并建议在中、 下承式拱桥的设计中使用无缝桥面板, 可以较大程度地降低吊杆的不同轴偏转。
1 吊杆不同轴偏转的理论分析
1.1 不同轴偏转角度和下锚固端最大弯曲应力计算公式的推导
目前, 单跨桥梁桥面板的主要约束方式为在桥梁两端采用可以产生纵桥向变形的支座, 如橡胶支座或滑动支座。此约束方式不是严格意义上的一端固支一端简支, 温度作用下桥面板将在桥梁两端产生程度相同的纵桥向变形。忽略桥面板在吊杆抗力下产生的微小弹性变形, 用来计算吊杆偏转角度和下锚固端最大弯曲应力的中、 下承式拱桥模型可以简化为如图3所示的计算模型(由于对称性, 取半边结构进行分析)。温度作用下, 桥梁中心线右侧第i根吊杆下锚固端的位移ΔLi为
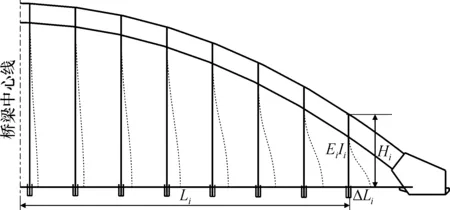
图3 吊杆不同轴偏转计算模型
ΔLi=αΔtLi,
(1)
式中:Li为第i根吊杆距离桥梁中心线的距离; Δt为温度变化;α为桥面板的温度膨胀系数[11]。
第i根吊杆的偏转角度θ(图4)为

图4 吊杆不同轴偏转角度
θ=ΔLi/Hi,
(2)
式中:Hi为第i根吊杆的长度。
单根钢绞线的截面惯性矩I为
I=πd4/64,
(3)
式中:d为钢绞线的公称直径, 则第i根由n根钢绞线组成的吊杆截面惯性矩Ii和抗弯刚度Ki分别为[12]
Ii=n·πd4/64,
(4)

(5)
式中:Ei为第i根吊杆中钢绞线的弹性模量。
根据形常数表[12], 第i根吊杆的杆端弯矩Mi为

=θ·(6EiIi/Hi+Hi·Ti),
(6)
式中:Ti为吊杆轴力, 通过式(6)可以看出, 吊杆下锚固端的弯矩主要受吊杆偏转角度θ影响。吊杆在下锚固端最大弯曲应力σb为
σb=Mi/Wi=d′/2Ii·θ·(6EiIi/Hi+Hi·Ti),
(7)
式中:Wi为吊杆截面截面抗弯系数,d′为吊杆直径。
通过上述理论推导, 得到了吊杆偏转角度和下锚固端最大弯曲应力的计算公式, 下文通过有限元分析对公式的准确性进行验证。
1.2 基于有限元分析对理论公式的验证
图5为中国东南地区某下承式拱桥模型, 跨径105 m, 共有12对吊杆, 每根吊杆由19根7Φ15.2 mm的钢绞线组成, 桥梁的合拢温度为5 ℃。该桥于2001年年底建成, 2010年发生过吊杆断裂事件, 对此桥进行有限元分析。 由于长度最短的吊杆不同轴偏转角度最大, 可以在较大范围内验证公式的准确程度, 因此选取最短吊杆的偏转角度和下锚固端最大弯曲应力与公式计算值进行对比(图6), 验证式(2)和式(7)的准确性。待公式的准确性验证后, 对该桥所有吊杆进行偏转角度和下锚固端最大弯曲应力的计算, 进一步研究不同轴偏转对吊杆的影响。
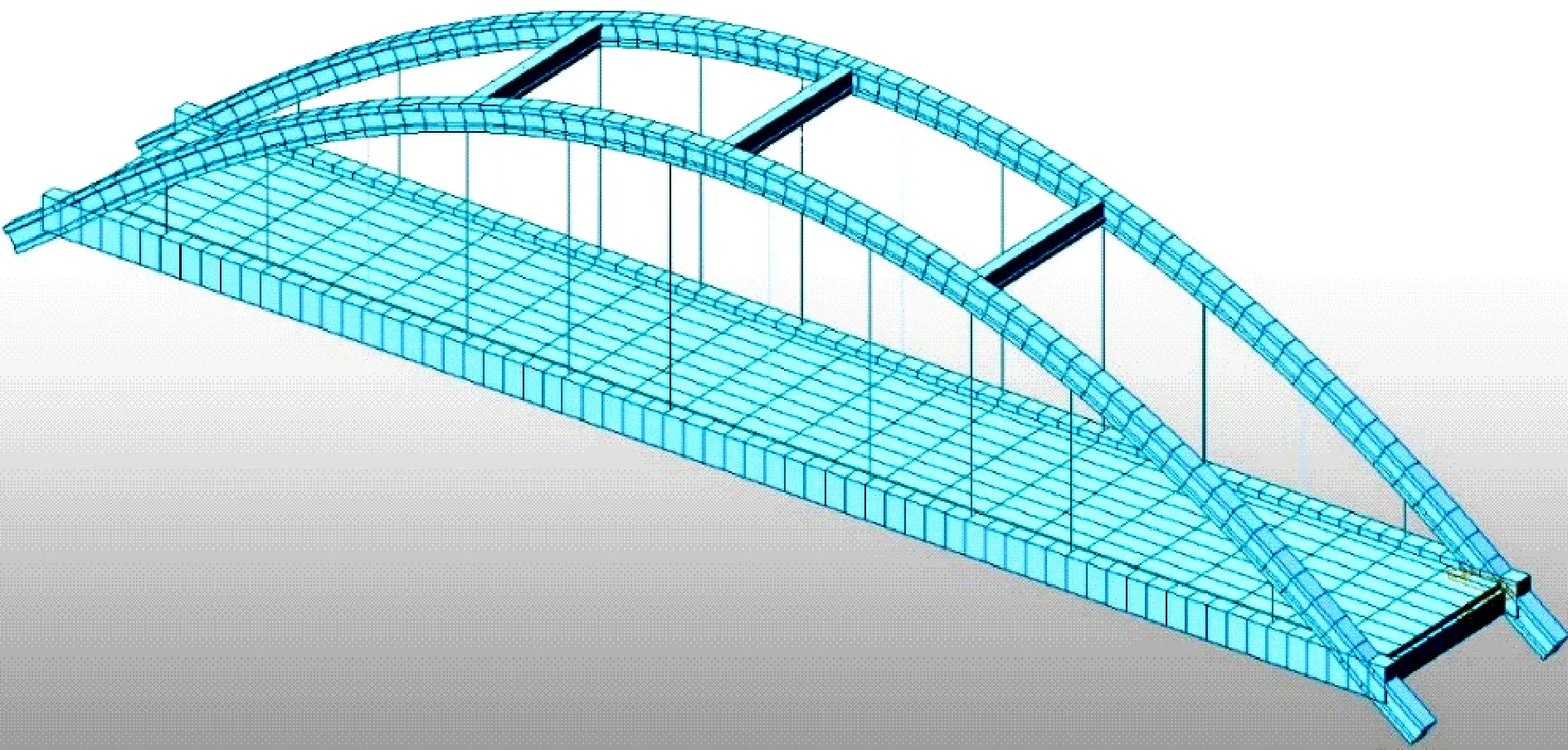
图5 下承式拱桥有限元模型

图6 不同温度下吊杆偏转角度(a)和锚固端最大弯曲应力(b)有限元分析和公式计算结果
可见, 公式计算值与有限元分析结果较为接近, 可用于进一步研究不同轴偏转对吊杆的影响。
1.3 不同轴偏转对吊杆的不利影响
该桥的合拢温度和所处地区最大温差为35.8 ℃, 篇幅所限, 表1只给出该温度下吊杆的偏转角度和下锚固端最大弯曲应力, 并与《钢管混凝土拱桥技术规范》(TB 5091—2013)中吊杆的容许应力进行了比较。

表1 吊杆不同轴偏转角度和下锚固端最大弯曲应力
可以看出, 距离桥梁中心越远、 长度越短的吊杆偏转角度越大, 下锚固端的弯曲应力也越大。吊杆的偏转角度最大可以达到18.55 mrad, 已经超出了规范对桥梁拉索或拉杆结构偏转角度的规定[13]。同时, 吊杆下锚固端的弯曲应力也达到了吊杆截面容许应力的56.5%。随着桥梁跨径的增长, 吊杆的偏转角度及下锚固端最大弯曲应力将更加明显。因此, 有必要关注不同轴偏转对吊杆产生的不利影响并进行进一步研究。
综合上述分析, 不同轴偏转实际上是将吊杆由轴向受拉构件变成拉弯剪构件, 受力状态如图7所示。 当轴向受拉构件受到较大弯矩和剪力的共同作用时, 其轴向抗拉强度将被削弱[12], 即偏转状态下的吊杆承载能力将被削弱。

图7 吊杆的在不同轴偏转下的受力状态
2 吊杆在不同轴偏转下的承载能力
2.1 不同轴偏转下吊杆的受力特点
目前规范中拱桥吊杆承载能力的校核方式为比较吊杆截面所受拉应力与容许应力的大小。
σt≤[σ],
(8)
式中:σt为吊杆横截面拉应力; [σ]为容许应力, 规范[13]中容许应力取0.33ftpk(ftpk为吊杆中钢绞线的抗拉极限强度, 由钢绞线的轴向拉伸试验得到)。但此承载力校核方式是基于吊杆作为轴向受拉构件, 拉应力在吊杆截面上均匀分布, 没有考虑不同轴偏转的影响。当吊杆发生偏转时, 其内部所有钢绞线不再均匀承受轴向拉力, 每根钢绞线的受力情况并不相同, 吊杆的承载能力不能视为所有钢绞线承载能力的总和, 而是由其中承受最不利荷载的单根钢绞线决定。因此, 可将吊杆视为纤维束模型(图8), 此时吊杆的承载能力由吊杆外侧承受最大弯曲应力的单根钢绞线的抗拉极限强度决定, 进而对钢绞线在不同轴偏转下的抗拉极限强度进行研究。

图8 吊杆承载能力校核模型
2.2 钢绞线不同轴偏转下的有限元分析
钢绞线的抗拉极限强度由钢绞线轴向拉伸时的破断力得到, 本节应用有限元分析考察钢绞线不同轴偏转下的破断力。目前桥梁拉索普遍采用抗拉强度为1 860 MPa的Φ15.2 mm钢绞线, 故以此级别钢绞线为研究对象。选用通用有限元程序ANSYS对钢绞线进行参数化建模。依据文献[14], 7Φ15.2 mm钢绞线的捻距应为钢绞线公称直径的12~18倍, 本文中钢绞线有限元模型的捻距取14倍, 由左向右捻制而成, 各根钢丝间的摩擦系数取0.2[15], 钢绞线的有限元模型如图9所示。

图9 钢绞线有限元模型
钢绞线的损伤模型采用延性断裂准则[16-17], 钢绞线损伤起始标准为
(9)
εpl=εpl(η),
(10)
式中:εpl为等效塑性应变,η为应力三轴度。
将钢绞线有限元模型设置不同的偏转角度并施加轴向拉力直至钢绞线断裂, 钢绞线断口如图10所示, 钢绞线破断力值见表2。在偏转状态下的钢绞线抗拉强度有了明显削弱, 偏转30 mrad时的破断力减小到195.9 kN, 比不偏转状态下减小了22%。

图10 有限元模拟钢绞线拉伸断裂
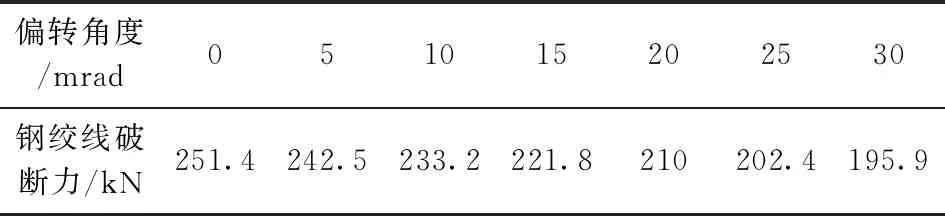
表2 钢绞线在不同偏转角度下的破断力值
2.3 钢绞线不同轴偏转下的拉伸试验研究
为验证钢绞线不同轴偏转下有限元分析的准确性, 对钢绞线在不同轴偏转下进行了拉伸试验。同样选用7Φ15.2 mm钢绞线, 试验装置如图11所示。对锚固钢绞线的锚板进行改造(图12a), 使被锚固的钢绞线可以偏转。目前世界最大跨拱桥——平南三桥的吊杆在温度作用下偏转角度最大可达30 mrad左右[18], 故试验中钢绞线的偏转角度上限设为30 mrad。由于锚板的面积所限, 在不影响锚板安全性能的前提下, 最多可以在锚板上设置3个偏转角。综上, 将试验中钢绞线的偏转角度设置为0、 10、 20、 30 mrad。

图11 钢绞线不同轴偏转下的拉伸试验

图12 钢绞线锚板(a)与钢绞线破断截面(b)

表3 钢绞线不同偏转角度下的破断力
对比有限元分析结果与试验结果(图13a和13b), 可以看出随着偏转角度的增大, 有限元分析结果与试验结果越接近。当偏转角度为0 mrad时, 两者试验误差为8.9%; 偏转角度为30 mrad, 误差为3.1%, 总体上误差控制在10%以内, 有限元分析结果较为理想。考虑到试验中每根钢绞线的性能与生产批次有关, 具有随机性, 因此选择有限元分析的拟合结果(图13b)进一步研究吊杆的承载能力。
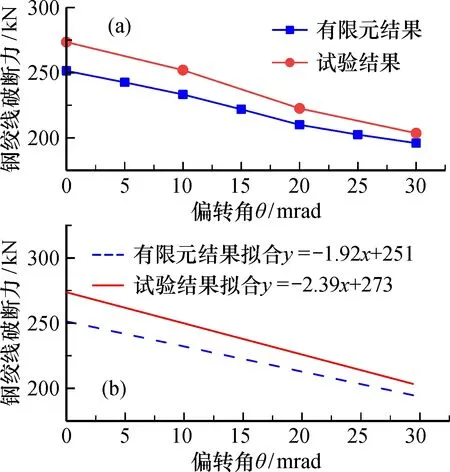
图13 钢绞线在不同偏转角度下的破断力(a)和钢绞线偏转角-破断力拟合曲线(b)
2.4 考虑不同轴偏转的吊杆承载能力校核方式
当不考虑不同轴偏转时, 规范吊杆承载能力按轴向受拉构件进行校核
σ≤0.33ftpk。
(11)
基于前文分析, 考虑不同轴偏转的影响, 中、 下承式拱桥吊杆承载能力的校核可视为对吊杆内承受最不利荷载的单根钢绞线的强度校核, 式(11)中的拉应力σ应包含不同轴偏转产生的最大弯曲应力σb,ftpk应采用偏转钢绞线的破断强度。根据图13b中钢绞线破断力和偏转角度关系的拟合曲线和吊杆下锚固端最大弯曲应力的计算公式, 对规范中吊杆承载能力的校核公式进行修正, 修正后的吊杆承载力校核公式为
σ+σb≤0.33(-1.92θ+251)/A,
(12)
式中:A为钢绞线截面面积;σb为吊杆下锚固端最大弯曲应力, 由式(7)可得;θ为吊杆偏转角, 由式(2)可得。考虑不同轴偏转影响的吊杆承载能力可由式(12)进行校核。
2.5 降低不同轴偏转影响的相应措施
对于未来中、 下承式拱桥的设计, 有必要采取相应措施降低不同轴偏转对吊杆承载能力的影响。根据上述结论, 提出可以在中、 下承式拱桥中采用无缝桥面板结构[19]以降低不同轴偏转对吊杆的影响。无缝桥面板结构为不设置伸缩缝的桥面系, 桥面板直接与桥台相连(无缝桥与设置伸缩缝桥梁的桥台对比见图14), 桥台将阻碍桥面板在温度作用下沿纵桥向的变形, 降低吊杆的不同轴偏转程度。马盛等[20]对无缝桥桥面板在温度作用下的纵桥向变形进行了研究, 本文式(2)可用于计算设置伸缩缝的桥面板在温度下的纵向变形, 因此可对桥面板在无伸缩缝和设置伸缩缝两种情况下的纵桥向变形进行对比, 进一步证明采用无缝桥面板措施可以减小桥面板的纵桥向变形, 降低吊杆的不同轴偏转程度。

图14 无缝桥桥台(a)与设置伸缩缝的桥台(b)构造对比
选取福建省某座上部结构为预应力混凝土T梁的无缝桥, 该桥合拢温度与当地年平均温度之差为25 ℃[21], 文献[20]已对该桥桥面板的纵桥向变形进行了研究。假设该桥设置伸缩缝, 应用式(2)对桥面板的纵桥向变形进行计算。在温差为25 ℃下, 将该无缝桥桥面板的纵桥向变形与设置伸缩缝时的纵桥向变形进行对比(图15)。

图15 设置伸缩缝桥梁与无缝桥桥面板纵向变形量对比
从对比结果可以看出, 相比于设置伸缩缝的桥面板, 无缝桥面板的纵桥向变形程度显著减小, 当桥梁跨度达到240 m时, 无缝桥面板的变形量较设置伸缩缝的桥梁减少了32.1%。由此, 建议在中、 下承式拱桥的设计中采用无缝桥面板结构, 以减小桥面板在纵桥向的变形, 降低吊杆不同轴偏转程度, 提高吊杆的实际承载能力。
3 结 论
(1)在温度作用下, 中、 下承式拱桥吊杆将会产生不同轴偏转。通过理论推导得到了吊杆不同轴偏转角度及其下锚固端最大弯曲应力的计算公式, 使用有限元分析对公式进行了验证,并结合一座下承式拱桥实桥进行了计算, 计算结果表明, 该桥吊杆在温度作用下产生了显著的不同轴偏转, 吊杆的下锚固端产生了较大的弯曲应力, 达到了容许应力的56.5%, 吊杆的承载能力将会被削弱。
(2)对组成吊杆的钢绞线进行不同轴偏转下的有限元分析, 得到了钢绞线偏转角度与破断力之间的关系, 并通过试验进行了验证。结合吊杆下锚固端最大弯曲应力的计算公式, 对规范中吊杆承载能力的校核方法进行了修正, 修正后的公式可用于考虑不同轴偏转情况下吊杆承载能力的校核。
(3)将无缝桥面板和设置伸缩缝的桥面板在温度作用下的纵桥向变形进行了对比, 发现无缝桥面板的变形程度显著小于设置伸缩缝的桥面板。提出在中、 下承式拱桥中可以采用无缝桥面板结构以降低吊杆的不同轴偏转程度, 提高吊杆的实际承载能力。
