航空复合材料壁板低速冲击损伤阻抗分析与测试实践*

于哲峰，朱 峤

（上海交通大学，上海 200240）

纤维增强复合材料在比模量和比刚度方面有着较大的优势，其中碳纤维层压板在航空结构上有着大量的应用[1]。由于纤维轴向有较高的强度和刚度，因此层压板有很好的面内承载性能。由于各层之间纤维方向不同，而相邻层在界面处的应变相同，因此在产生弯曲时会产生较大的层间应力[2-3]。飞机结构在运营过程中不可避免地受到外物的冲击，如掉落的工具、跑道的碎石、冰雹、搬运中的磕碰等，这种冲击对层压板产生的是面外集中载荷，容易在接触点产生基体裂纹，逐步扩展到层间，面外载荷也同时产生弯曲，所以层间应力的存在使裂纹继续扩展，从而形成分层损伤[4-5]。

板的弯曲刚度与其厚度的立方成正比，分层损伤使层压板局部的弯曲刚度严重降低，而板的受压失稳临界载荷与弯曲刚度成正比，所以分层会导致其受压失稳临界载荷降低，从而使得外加载荷小于预期设计临界载荷时，结构就会发生破坏[6]。因此冲击后剩余压缩强度成为了层压板的关键性能参数，通常采用标准试片的冲击后压缩试验（Compression after impact，CAI）来测量这个参数，从而为整体部件的分析和设计提供参考。

随着对复合材料轻量化要求的提高以及工艺的进步，大型整体结构越来越多，如翼梁、纵墙、长桁会与蒙皮共固化。根据复合材料结构的“积木式”验证理念，需要进行结构部件冲击后的损伤评估，所以要开展复合材料整体结构的冲击损伤及测试，于是产生了新的测试问题。作者所在的上海交通大学民机结构强度综合实验室在多个军、民飞机课题中，开展了多项复合材料整体结构冲击问题的研究，积累了一定试验和损伤分析技术。本文将从响应模型、损伤机理和试验方法来对复合材料层合结构的冲击问题进行介绍。

复合材料板的冲击响应模型

1 复合材料板的冲击动力学方程

基于薄板的弯曲理论，忽略剪切变形的影响，矩形正交复合材料层压板在横向动态载荷P（t）冲击作用下的弯曲微分方程可以表示为[1，7]：

式中，Dij为根据经典层压板理论得到的弯曲刚度矩阵系数；mp为单位面积质量；wp=wp（x,y,t），为层压板的挠度。

利用杜哈梅积分，层压板的挠度可以表示为[8]：

式中，Lx和Ly分别为层压板的长度和宽度；ωmn为对应（m,n）阶模态的固有频率；φmn（x,y）为（m,n）阶模态振型函数；（xi,yi）为层压板表面冲击载荷作用点的坐标。

冲击过程的载荷是由冲击体与层压板的接触产生的，考虑到冲击凹坑的影响，由Hertz 接触定律[9]，冲击载荷可以表示为：

式中，Kc为接触刚度，wi为冲击体的位移，而冲击体视作刚体，其运动方程为：

式中，mi为冲击体的质量，通过联立求解式（2）～（4）3 个方程即可得到层压板的冲击响应。本文作者基于该方法，并结合摄动法模拟损伤对模态产生的干扰，实现了小质量冲头作用下的响应预测[10]。

2 准静态冲击响应模型

式（2）所给冲击响应考虑了层压板自身高阶振动模态的影响，对于质量较小的冲击体，冲击接触的时间很短，层压板的高阶模态对响应影响明显且不可忽略。随着冲击体的质量增大，其与层压板所组成的冲击系统固有频率也会随之降低，接触时间变长。对于板而言，相当于受到一个低频的载荷，因此高阶模态响应很弱，故在冲击模型的建立过程中只考虑低阶模态即可。Olsson[11]依据冲击体与结构的质量比，对薄板结构的冲击响应类型进行了划分，冲击体与结构质量比小于0.23 时，冲击响应受高阶模态影响较大，定义为小质量冲击问题，而当质量比大于2 时，低阶模态在结构冲击响应中占主导地位，定义为大质量冲击，视作准静态响应，质量比介于0.23～2 之间的情况定义为中等质量冲击。

对于大质量冲击，只考虑板的第一阶振型即可，进而可以引入广义单自由度系统来描述冲击点的响应[12]，进一步结合结构的模态振型函数，得到其整体响应。Shivakumar等[13]提出弹簧-刚度模型来描述接触区域冲击体与结构之间的耦合，同时考虑了薄膜刚度对冲击响应的贡献，可以得到冲击点处响应的完整时间历程：

式中，Kb和Km分别为层压板的弯曲刚度和薄膜刚度。文献[13]中给出的弯曲刚度和薄膜刚度表达式是基于圆形板冲击问题推导得到的，而对于工程中常见的矩形板而言，可用与其面积相等圆形板的等效半径r*来表示[14]。

当冲击体位移和层压板冲击点处的挠度之间的差异，即冲击凹坑深度相较于结构整体的挠度可以忽略时，Abrate[14]提出了一种简化的单自由度弹簧-刚度模型，即将冲击体与层压板冲击点处的位移视为一致，w=wi=wp，忽略板的质量mp，此时式（5）可以简化为：

对于准静态过程，Shivakumar等[13]也给出了一种无需求解动力学微分方程的能量等效方法，根据层压板弯曲、剪切等变形下的应变能与冲击体动能相等的条件，求解得到最大冲击载荷，但该方法不能给出冲击过程的时间历程曲线。

冲击损伤特点

对于厚度不同的层压板，冲击损伤发展的形式有所不同。以正交铺层板为例，对于厚板（图1（a）），局部的高应力首先引起冲击接触点的基体开裂，然后基体的裂纹向层间扩散。而对于薄板（图1（b）[15]），冲击点背部弯曲应力首先引起基体的开裂，然后再向层间扩展。

图1 正交铺层板的两种损伤模式Fig.1 Two kinds of damage model of orthogonal layer board

层压板一旦产生分层损伤，其承受面外法向载荷的能力将大幅降低，即使进一步遭受到较小的冲击载荷也会导致裂纹继续扩展，所以对于层压板而言，建立合适的分层损伤临界载荷模型就显得尤为重要。在假定层压板没有损伤情况下，应用冲击响应模型能够得到冲击载荷历程，当冲击载荷达到预估的临界值时，则判断结构出现分层损伤，从而进行模型刚度的折减，模拟含损伤的响应历程。

目前，层压板分层损伤临界载荷模型主要有两类：基于断裂理论的模型和基于剪切强度的模型。

1 基于层间断裂理论的分层临界载荷模型

该模型最早由Davies 等[16]提出，他们首先讨论了一种分层损伤面积的预测方法，认为损伤是层压板在外载荷作用下，板内的最大剪切应力超过了其剪切强度，从而导致分层的产生，而在剪切应力小于剪切强度τzr的区域，分层不再扩展，由此得到了层压板中分层损伤的大致范围。该方法体现了分层损伤与层间剪切强度有关的朴素思想，假定层压板的厚度为t，接触区域为半径为a的圆，则层压板内最大剪切应力为边界上平均剪切应力的1.5 倍，即：

由此可以得到分层区域面积为：

然而，试验测量得到的结果与该模型预测并不相吻合，很多情况下，分层面积都是在接触力达到某一特定值后突增，随后随接触载荷的峰值呈现一定正比例关系，这种现象更适合用断裂理论来解释，所以他们又根据层间断裂理论进行了研究。假定层压板内发生分层，则可以导出层间Ⅱ型开裂的应变能量释放率为：

式中，E为材料的弹性模量，μ为泊松比，t为层压板的厚度。

GⅡ与分层损伤的初始半径无关，故应用该模型分析其扩展过程时，不需要预先假设层压板中初始裂纹的长度，而是随着载荷P的增大，GⅡ达到临界值GⅡc时，分层即发生扩展。由式（10）可知，层压板发生分层的临界载荷Pcr为：

由此可见，在材料的弹性模量E和临界能量释放率GⅡc确定的情况下，分层的临界载荷Pcr与t1.5成正比，该结论也在Schoeppner 等[17]的研究中得到了证明。

2 基于层间剪切强度的分层临界载荷模型

基于断裂理论的分层临界载荷模型并没有考虑冲击体的形状，无论冲击体的形状如何，只要产生了足够的接触载荷，就会导致分层的扩展，然而冲击损伤的萌生与冲击体形状是密切相关的。基于层间剪切强度的损伤模型是在考虑冲击体形状的前提下，通过计算层压板接触区域的剪切应力分布，判断其是否达到层间剪切强度τzr来确定冲击损伤的发生。

根据Hertz 接触定律，假设冲击体为半球形，其与层压板接触时，接触区域的半径可以表示为[18]：

式中，E*为接触刚度，R为冲头半径。

球形冲头产生的圆形接触区域边缘上的平均剪切应力可以表示为：

当达到层间剪切强度τcr时，即可判断层压板出现分层，结合式（12）和（13）可得：

由式（14）可见，分层损伤的临界载荷仍然与t1.5成正比，Yang 等[19]的研究也很好地验证了这个结果，这个临界载荷模型不仅考虑了冲头半径的影响，也包含了局部应力对材料损伤的影响。该模型仅对圆形冲击体有效，对于其他形状的冲击体还有待发展。

3 考虑结构挠度影响的分层临界载荷模型

上述基于层间剪切强度的模型是在Hertz 接触理论的基础上得到的，而该理论适合被接触物体厚度远大于自身挠度的情况。然而，航空结构中的层压板厚度有限，而冲击载荷作用下的挠度变形相对较大，挠度会对接触特性产生明显影响。南京航空航天大学的Chen 等[20]针对这一现象，提出了改进的Hertz 接触定律，引入结构挠度对接触应力的影响，预测了不同接触力下的凹坑深度，结果表明考虑挠度影响后，同样接触力下凹坑深度会减小，这与试验结果也更为吻合。

凹坑深度减小，实际上是由于接触面积增大导致的，更大的接触面积降低了接触应力，式（14）所示的模型是根据接触区域边缘上的平均剪切应力推导出来的，因此需要更高的接触载荷才能使层间剪切应力达到剪切强度τcr。作者针对这个问题对基于层间剪切强度的分层临界载荷模型进行了改进[21]。

考虑层压板自身的挠度之后，冲击体和层压板之间的接触区域见图2，a和a*分别为考虑挠度前后的接触半径，wa和wa*为对应的挠度，w0为接触区域中心的挠度，α0和α0

图2 考虑挠度影响的接触区域示意图Fig.2 Sketch of contact area considering deflection effects

*分别为接触区域中心和边缘的压入深度，由几何关系可以近似表示出a*：

在不考虑挠度影响的情况下，计算得到分层损伤的临界载荷Pcr，然后由薄板弯曲理论可知接触区域各位置的挠度为：

式中，r为层压板的半径，D为等效弯曲刚度。联立式（15）～（18），运用数值方法可以求解修正后的接触区域半径a*，根据这个接触半径和层间剪切强度，即得到修正后的分层损伤临界载荷P*cr

将该模型应用于5 种不同厚度的复合材料壁板区域的分层损伤临界载荷预测，得到结果如图3所示，相比于线性模型，改进模型结果与试验结果吻合更好，很好地反映了试验结果分布的非线性特征。

图3 不同分层区域的分层临界载荷Fig.3 Layered critical load of stratified area

4 复合材料胶接区的分层临界载荷模型

复合材料壁板是航空工程中常用的薄壁结构，经常由蒙皮与加强筋或者翼梁共固化而成，如图4所示为多梁的复合材料翼盒截面，其上下蒙皮和翼梁使用共固化方式胶接，两翼梁之间蒙皮处（图4中类型A的位置）的抗冲击性能与四边简支板近似，应用基于层间断裂理论或者基于层间剪切强度的模型可以得到该类型冲击点的分层临界载荷。对于类型B的位置，作者在文献[22-23]中提出了对应冲击分层损伤临界载荷模型。

图4 多梁翼盒冲击区域示意图Fig.4 Impact area sketch of more beam wing box

类型A蒙皮处的厚度为t，类型B处的厚度为t1，类型A处的分层临界载荷Pcr,A与t的1.5 次幂成正比，而类型B处有一半区域的厚度增加了（t1-t），使得分层损伤临界载荷增加了，于是可以得到类型B处的分层临界载荷为

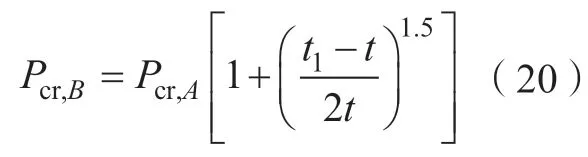
式中，Pcr,A可以由基于层间断裂理论的分层临界载荷模型和基于层间剪切强度的分层临界载荷模型所述两种模型计算得出，也可以通过对类型A蒙皮进行冲击试验测得。某型翼盒两个不同区域的铺层参数及厚度如表1所示，各类型冲击点处的接触力曲线如图5所示，根据接触力曲线突降处的值确定Pcr,A，应用式（20）计算Pcr,B，误差分别为10.2%和5.7 %。

图5 两个不同区域的接触力曲线Fig.5 Contact force curves of two areas

表1 某型翼盒不同区域铺层参数及厚度Table 1 Different regions of a certain type of wing box layer parameter and thickness

在翼梁顶端的位置，即图4中类型C处，冲击损伤一般不明显，冲击凹坑也较浅，其冲击接触力曲线如图6所示，可以看出，接触力曲线上没有对应于临界载荷的突降出现。而对于长桁加强壁板结构，类型C处下部没有很强的支撑，容易出现冲击损伤。图7所示为一长桁加强壁板C型位置处的冲击力曲线，在对应临界载荷处的突降也较为明显。

图6 多梁翼盒类型C 点处冲击接触力曲线Fig.6 C impact point contact force curve of multi-beam wing box

图7 某长桁加强壁板类型C 处冲击接触力曲线Fig.7 C impact contact force curve of a long plate girder strengthened wall

落重冲击试验技术

在大型壁板结构上进行落重冲击试验的基本要点可以参考ASTM D71360[24]。落锤的重力势能在自由下落过程中转化为动能，通过调节其初始下落高度，可以控制冲击初始速度的大小。通过安装测力、测速传感器来实现冲击力和初始冲击速度的测量。为了保证冲击位置与预设目标一致，落锤下落过程中的导向方式通常采用导筒或者导轨，如图8所示，实践表明采用导轨的导向方式更加便于操作，同时，冲击体下落过程中的摩擦耗能也相对稳定。

图8 壁板结构表面落重冲击试验Fig.8 Drop impact test wall structure surface

落重冲击试验中，落锤的初始冲击速度对于整个冲击过程的分析是重要的参数之一，使用开孔测速板与高速光电开关组成的测速组件可以实现初始冲击速度的测量。如图9所示，固定在落锤上的测速板设置有矩形孔，在冲击体下落过程中这个孔划过光电开关的光路，从而在数采系统中产生具有时间差的触发信号，如图10 所示。测速板下沿开始阻挡光路后，在t1时刻产生第1 个下降沿，同样，随后光路接通，信号恢复，当孔的上沿开始阻挡光路后，在t2时刻又产生第2 个下降沿。数采系统同步采集力信号，在ti时刻冲头开始与结构发生接触，t1与t2之间的时间段落锤仍然在重力加速度作用下作加速运动。参照ASTM-D7136 中所给的修正公式，ti时刻落锤的速度vi可以表示为

图9 落锤及测速、测力原理示意图Fig.9 Drop weight and speed,load principle diagram

图10 力传感器和数字激光传感器试验测得信号Fig.10 Measured signals by force sensor and digital laser sensor test

式中，d12为测速板下沿和孔上沿之间的距离，如图 9 所示；g为重力加速度。

使用接触力信号可获得落锤的加速度时间历程，积分后可以得到落锤的速度、位移以及冲击能量的时间历程。需要注意的是，经过积分处理之后，这些时间历程数据的点数都会减小。

关于试验过程中落重冲击试验机的安装，在条件允许的情况下，对于尺寸较小的加筋壁板结构，应搭建安装支架，从而避免试验机自身重量对试件的动力学特性产生影响。而对于诸如整体翼盒、整段舱体等具有较大刚度的结构，试验机可直接放置在结构表面实施冲击试验。对于需要试验人员站立在结构上开展试验的情况，为了尽量减小人体重量对冲击响应的影响，试验人员应站在靠近支撑端一侧，即冲击点与结构固定端之间，这样使得冲击点处预应力仅是由结构和试验机自重引起的[24-26]。

结论与展望

（1）复合材料冲击损伤理论经过多年的发展，对于典型壁板区域已经有若干种有效的损伤预测模型，预测结果与试验的统计值吻合较好，但试验数据本身的离散度较大，这一点在使用时仍然需要注意。对于较为复杂的结构，如本文图 4 中所示的C型区域，还缺乏响应和损伤预测的解析方法，类似的典型区域还有若干种，其冲击响应和损伤演化预测技术是值得探索的。

（2）大质量准静态冲击的建模和测试比较成熟，甚至可以用准静态压缩过程替代，但值得注意的是，准静态压痕试验的损伤起始载荷会低于低速冲击试验得到的结果，这个现象可以根据惯性力和应变率效应来解释。如果结构受冲击影响的区域较大，结构刚度相对变低，高阶模态响应增多，冲击体和结构之间耦合效应增大，这时响应过程复杂，响应规律不易总结，在实施冲击损伤引入要逐步地尝试才能获得期望的损伤效果，通常一种方法只针对特定结构有效，因此等效测试方法和损伤经验模型的发展对工程应用都具有很好的意义。

（3）大部分测试技术都采用重力势能来产生冲击动能，通过导轨转换落锤运动方向可实施对不同方向结构表面的冲击，这种能量转换方式与测试设备的便携性和可操作性之间存在矛盾，由此，可探索更加便利且实用的能量转换方式，如弹性能等，可适用于更多场景的试验。