弹性支撑杆下变悬点单摆运动的研究
2021-08-19田蓬勃刘瑞丰方爱平王小力
周 颖,田蓬勃,李 涛,刘瑞丰,刘 萍,方爱平,王小力
(1.西安交通大学 电气工程学院,陕西 西安 710049;2. 西安交通大学 物理学院,陕西 西安 710049 )
单摆是一个古老的数学物理模型,又一直是很多新概念提出的源泉.由理想单摆衍生出来的倒摆、复摆、球面摆、共振摆等模型一直吸引着人们的关注.同时由于其在大角度释放时运动学方程的非线性特征,使其成为大学物理教学中混沌现象和非线性问题研究很好的切入点.目前针对摆长可变[1],施加侧向扰动[2],弹簧耦合摆[3]等情形下摆球分别做水平面内振荡和竖直面内振荡[4]已有充分研究,但大多着重于对运动周期、相图的研究,不具备直观性.对于能直观表示摆球运动的轨迹图,以及摆平面的分位移图较少关注,且大多数模型都对摆角做小角度线性处理,使其结论不适用于大角度释放的情况.同时,上述系统的支撑杆皆为刚性杆,对于弹性杆作为支撑杆的情况下,单摆出现振荡方向逐渐转变的情况尚无系统的研究.本文旨在从理论到实验系统研究水平支撑杆为弹性杆时,摆球的运动轨迹和振荡方向改变90度的时间,重点分析摆球运动的轨迹形状和影响振荡方向相对初始运动方向转过90度所需时间的因素.
1 理论基础
1.1 水平弹性杆运动模型简化与参数确定
如图1所示,设有一个单摆系统,其中水平弹性杆长度为L,一端固定在竖直的刚性支撑架上,另一端(前端)绑定绳子以避免弹性杆在运动过程中竖直方向的偏转.同时在弹性杆前端悬挂一根摆线,记弹性杆与摆线的连接点为A(悬点A),摆线质量不计且长度为l,下端悬挂质量为m可视为质点的小球.以A点为坐标原点,建立如图1所示直角坐标系Oxyz.

图1 弹性杆做水平支撑杆的单摆模型图
从某一角度θ释放摆球,摆球在运动过程中通过摆线挤压或拉伸弹性杆,弹性杆在水平面内发生形变.这里我们将弹性杆在水平面内的运动简化成沿x轴和沿y轴两个垂直方向上弹簧运动的耦合.简化理由是设摆球的振荡频率为ω,弹簧振子的固有频率为ω0,弹簧振子受到摆球通过摆线耦合的周期性作用力为fsin(ωt+φ),则弹簧振子的动力学方程为
(1)
对于一般的弹性杆而言,存在ω<<ω0,则在一段比较小的时间内可以近似认为弹簧振子受到的作用力为恒力,则弹簧的位移和速度可以分别表示为
(2)
(3)
相当于该弹簧振子以自身的固有频率ω0做高频振荡,而该高频振荡的平衡位置又随着摆球施加的周期性作用力做频率为ω的低频振荡.又由于ω<<ω0,则速度表达式中低频项近似可以忽略,故可认为弹簧振子以其自身固有频率做简谐运动.设沿着支撑杆方向摆放的弹簧劲度系数为kx,垂直于杆方向的弹簧劲度系数为ky,悬点A的运动是两个弹簧振子运动的叠加,如图2所示.
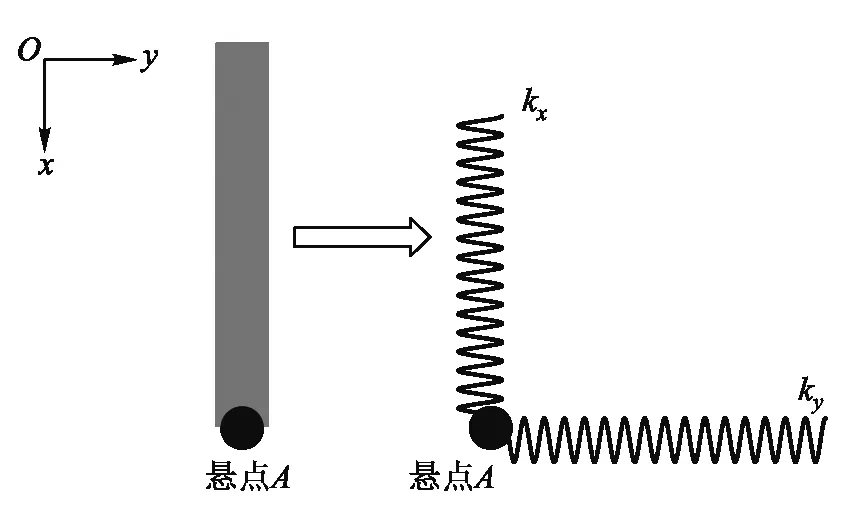
图2 弹性杆的二维简化模型

1.2 保守系拉格朗日方程
空气阻力F的计算公式[7]为
(4)
式中C、ρ、S、v分别为空气阻力系数、空气密度、物体迎风面积、物体速度.
实验使用的摆球用砝码代替,迎风面积S=5.4 cm2,砝码质量m=50 g,空气密度ρ=1.2 kg/m3,空气阻力系数C=1.0.当摆球的运动速度v=1 m/s时,空气阻力F=0.0003 N.该力的大小仅相当于摆球重力的0.61 ‰。因此理论分析中可以忽略空气阻力的影响,近似认为该单摆体系为理想保守系.
首先对沿着杆的轴向释放摆球的情况进行分析.设x,y,z轴方向上的单位向量分别为i,j,k, 弹性杆沿着x轴水平放置,摆球在Oxz平面内释放.设悬点A点的运动方程为r=x(t)i+y(t)j,两个等效弹簧的运动方程可写成:x(t)=Axcosωxt,y(t)=AysinωyA,式中A,ω分别是弹簧振幅和振动频率.由几何关系得到摆球运动方程为
R=r+lsinθcosφi+lsinθsinφj-lcosθk
(5)
摆球的动能为
(6)
考虑到在后续拉格朗日方程的计算中,上式中的动能交叉项远小于动能的非交叉项,为简化计算,忽略上式交叉项,化简为
(7)
系统总势能U等于摆球重力势能与两个弹簧的弹性势能之和,即
(8)
对选取的4个广义坐标x、y、θ、φ列写拉格朗日方程,代入化简最终得到描述摆球运动的微分方程组:
(9)
对于摆球在Oyz平面内释放情况类似,其运动的微分方程为
(10)
下面我们在特定的实验参数下对上述方程进行数值求解.摆球用标准砝码代替,假设摆球沿轴向释放,摆线长l=19.00 cm,摆球质量m=50 g,初始摆角θ=70.8°,支撑杆为纵纹木杆,E=10 Gpa,I=52.08 mm4,且质量ms=11.04 g,长度为22.85 mm,横截面积S=25 mm2,悬点A的Ax=0.1 mm,ωx=3.15×104rad/s,Ay=0,ωy=4.87×103rad/s.将以上参数带入到MATLAB数值计算程序中进行求解,得到摆球的理论俯视轨迹图如图3所示,其中横坐标x方向为支撑杆的轴向,纵坐标y方向为支撑杆的切向.该图说明了当支撑杆为弹性杆时,从杆的轴向释放摆球,摆球的俯视轨迹会按照类似一系列进动的椭圆轨道的形式逐渐转变摆动方向,实现整个平面内摆动.分位移图如图4所示,可以更直观地看出摆球摆动时,其轴向分位移和切向分位移呈现周期性的交替消长的变化趋势.
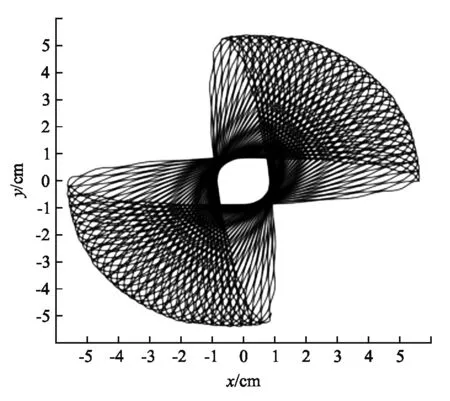
图3 轴向释放摆球时,摆球的理论俯视轨迹
2 实验部分
实验装置如图5所示,器材为铁架台,砝码,棉线,木杆,硬质PVC杆.其中右侧铁架台为主实验装置,左侧铁架台通过棉线与砝码绑紧,作为摆球初始释放辅助装置.实验中采用剪断棉线的方法来释放砝码,避免手动释放砝码带来的附加速度和角度偏差.我们通过改变摆球的初始释放角、摆线长度和支撑杆的杨氏模量,分析这三个参数对摆球的振动方向在两个垂直方向(即支撑杆的轴向和切向)之间转化的时间以及摆球轨迹的影响.在数据记录分析方面,我们选择以单个铁架台两脚之间的直线距离作为长度参照,并利用手机相机以每秒29帧的速率记录俯视方向上摆球运动的轨迹(将摄像头固定在悬点的正上方,微调摄像头的位置使其正对着支撑杆的中轴线,并调好焦距).然后使用视频分析软件TRACKER追踪每一帧摆球的位置坐标(如图6所示),再将数据导入MATLAB,对比分析理论曲线和实验数据.

图5 实验装置图

图6 TRACKER软件分析视频窗口
2.1 改变初始释放角
支撑杆选用纵纹木杆,其杨氏模量为E=10 Gpa,质量为ms=11.04 g,长度为l1=31.10 cm,横截面积S=25 mm2.单摆摆线长l=22.85 cm,摆球质量m=50 g.实验开始时沿着支撑杆的切向释放摆球,并改变摆球的初始释放角.
图7(a)与7(b)分别展示了初始释放角为39.2°和30.8°时摆球的切向分位移图.从图中可以看出在摆球的振荡过程中,其切向分位移的幅度在振荡衰减.当释放角为39.2°时,摆球在释放后40秒左右切向分位移减小到0 cm,即摆球振动的方向从沿着支撑杆的切向完全转化为沿杆的轴向.当释放角为30.8°时摆球在44秒左右其切向分位移同样减小到0 cm.同时由于理论分析中忽略了空气阻力以及实际器械各部分连接处摩擦力的影响,图7(a)与7(b)中理论曲线的幅度都比实际轨迹的幅度略大.
定义摆球从杆的轴向(切向)释放开始,到其运动方向刚好转变为沿杆的切向(轴向)的时间为摆球运动方向的转化时间.同理,摆球运动方向的理论转化时间为从Oxz(Oyz)平面内释放摆球开始,到摆球在该振荡平面内的分位移幅度衰减为0的这段时间,实验中可通过观察摆球运动方向刚好转过90度来得到实验转化时间.进一步地,将从不同角度释放摆球时,摆球的理论转化时间和实验转化时间列在表1中.从表中可以看出在相对误差较小的情况下,初始释放角越大,转化时间越短.理论转化时间随释放角的变化曲线和实验测得数据点如图8所示,同样可以看出释放角越大,摆球振动方向从支撑杆的切向完全转化为轴向的时间越短.

图7 从支撑杆的切向沿着不同摆角释放 摆球时,摆球的切向分位移图

表1 不同初始释放角时摆球运动方向的实验转化时间以及理论转化时间

图8 摆球运动方向的转化时间随初始释放角的变化
2.2 改变不同摆长
保持摆球质量m=50 g,支撑杆为纵纹木杆,杨氏模量E=10 Gpa,质量ms=11.04 g,长度l1=31.10 cm,横截面积S=25 mm2,初始释放角θ=39.2°.实验过程中沿着支撑杆切向方向释放摆球,并改变单摆的摆线长度.

图9 在不同摆线长度下从支撑杆的切向释放摆球时,摆球的切向分位移图
图9(a)与9(b)分别展示了摆线长分别为31.1 cm和22.7 cm时摆球的切向分位移图.从图中可以看出当摆线长在31.1 cm时,摆球在38秒左右切向分位移减小到0 cm;当摆线长在22.7 cm时摆球运动的转化时间在30秒左右.
针对31.1 cm, 22.7 cm, 11.3 cm和3.1 cm长度的摆线,摆球的理论转化时间和实际转化时间列在表2中,从表中可以看出摆线长度越短,转化时间越短.同时做出理论转化时间随摆线长的变化曲线和实验测得数据点如图10所示,图10表明摆线长度越短,摆球振动方向从切向完全转化为轴向的时间越短.

表2 不同摆线长度时摆球运动方向的实验转化时间以及理论转化时间

图10 摆球运动方向的转化时间随摆线长度的变化
2.3 改变支撑杆材料
保持摆线长l=21.10 cm,摆球质量m=50 g,支撑杆长度l1=31.10 cm,横截面积S=25 mm2,初始释放角θ=39.2°不变.实验过程中沿着杆切向方向释放摆球,并改变支撑杆的材料.
图11(a)与11(b)分别展示了采用纵纹木杆(杨氏模量E1=10 Gpa)和硬质PVC杆(杨氏模量E2=0.24 Gpa)作为支撑杆时摆球的切向分位移图.从图中可以看出当支撑杆是纵纹木杆时,摆球在38秒左右切向分位移减小到0 cm;当支撑杆是硬质PVC杆时,摆球的转化时间在20秒左右.
由此得到使用上述两种不同材料的支撑杆的情况下,摆球的理论转化时间和实际转化时间如表3所示.从表中可以看出支撑杆的弹性越大,摆球运动方向的转化时间越短.在图12中做出理论转化时间随弹性杆杨氏模量的变化曲线,同样可以看出摆球从切向到轴向运动的转化时间与支撑杆的弹性成负相关.

图11 从不同材料支撑杆的切向释放摆球时,摆球的切向分位移图

表3 不同材料支撑杆下摆球运动方向的实验转化时间以及理论转化时间
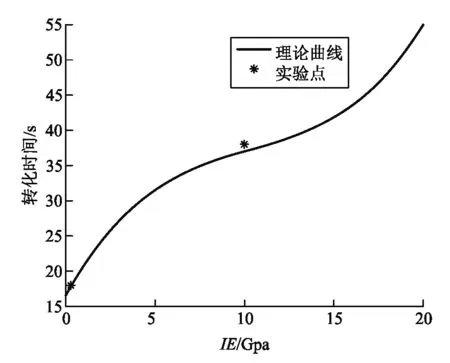
图12 摆球运动方向的转化时间随弹性杆杨氏模量的变化
3 小结
本文首先将水平弹性支撑杆的平面运动转化成两个垂直方向上弹簧运动,在验证了外界阻尼可忽略的前提下利用保守系拉格朗日方程得到摆球运动的微分方程组,通过数值计算给出单摆运动的轨迹图及转化时间等关键参数,进而系统地总结出弹性支撑杆下单摆运动的规律.
同时采用实验室常见器材进行实验.针对支撑杆为弹性杆时,摆球沿杆轴向和切向运动的自发转化问题,研究了初始释放角,摆线长度和支撑杆弹性系数对摆球运动转化时间的影响,取得如下主要结论:
1) 初始释放角越大,转化时间越短;
2) 摆长越短,转化时间越短;
3) 弹性杆弹性越大,转化时间越短.
4 致谢
感谢刘瑞丰、赵述敏、刘萍、李荣、孔春才等指导老师,是他们的严格要求和悉心的指导使本文逐步完善.感谢袁识博、蒋施达同学对于理论分析的帮助.感谢张俊武、王雪冬老师对于实验的帮助.
