恒定磁场中安培环路定理的探讨

胡锡奎，李 丽，冯春宝，牟 琼

(重庆邮电大学 理学院，重庆 400065)

安培环路定理是稳恒磁场最重要的定理之一，反映了磁场的涡旋性以及恒定磁场与电流的关系，是学生必须掌握但概念容易混淆的一个定理，其具体表达式如下

∮lB·dl=μ0∑Iin

(1)

其具体意义为：在真空的恒定磁场中，磁感应强度沿任一闭合曲线(回路)的路径积分(即B的环流)的值，等于真空的磁导率μ0乘以穿过以该曲线所包围的各恒定电流的代数和[1-3].

1 安培环路定理应用的探讨

相对于毕奥-萨伐尔定理，安培环路定理具有更简洁的形式，常用于计算恒定电流所产生的磁场的磁感应强度分布[4,5].在一般的恒定电流情况下，安培环路定理公式等号右侧电流的代数和很容易计算，但公式等号左侧的路径积分计算比较困难，甚至需要利用数值计算软件[6,7].因此，在利用安培环路定理求解恒定电流的磁感应强度分布时，要求恒定电流的分布具有特殊的对称性，其磁感应强度的分布也具有相应的对称性.可以选择一个合适的积分回路，使得回路上各点的磁感应强度的方向与回路的方向平行或者垂直，且在有效的回路区域上各点的磁感应强度大小相等.此时，路径积分很容易计算，安培环路定理可以简化为

∮lB·dl=BL=μ0∑Iin

(2)

其中，B为磁感应强度的大小，L为有效的回路长度(回路中B·dl≠0的区域的长度，即磁感应强度大小不为零且磁感应强度的方向与回路的方向不垂直).相应的磁感应强度的大小为

(3)

常用无限长载流直导线体系说明安培环路定理在磁感应强度计算中的应用.如图1所示，无限长载流直导线是柱对称的，其磁感应强度的分布也应该是柱对称的.以无限长载流直导线为轴的圆柱面上，各点的磁感应强度的大小相等，且磁感应强度的方向与该点处圆柱面的水平切线平行.选择以直导线为轴的圆作为回路，回路的正方向由电流方向的右手螺旋关系确定.

无限长载流直导线中的电流为I，回路上各点的磁感应强度的大小都为B，且磁感应强度的方向与该点的回路方向相同.回路的半径为R，有效长度为L=2πR.利用式(3)可得无限长载流直导线产生的磁感应强度的大小为

(4)

式(4)与毕奥-萨伐尔定理求解和实验测量得到的磁感应强度分布一致，但计算过程较毕奥-萨伐尔定理简单，证明了安培环路定理在求解具有特殊对称性的电流体系的磁感应强度分布时非常方便.除了无限长载流直导线外，安培环路定理还常用于处理无限长柱对称载流体系、无限大平面载流体系、无限长直通电螺线管、通电螺线绕环等具有特殊对称性的电流体系，计算过程非常简单.

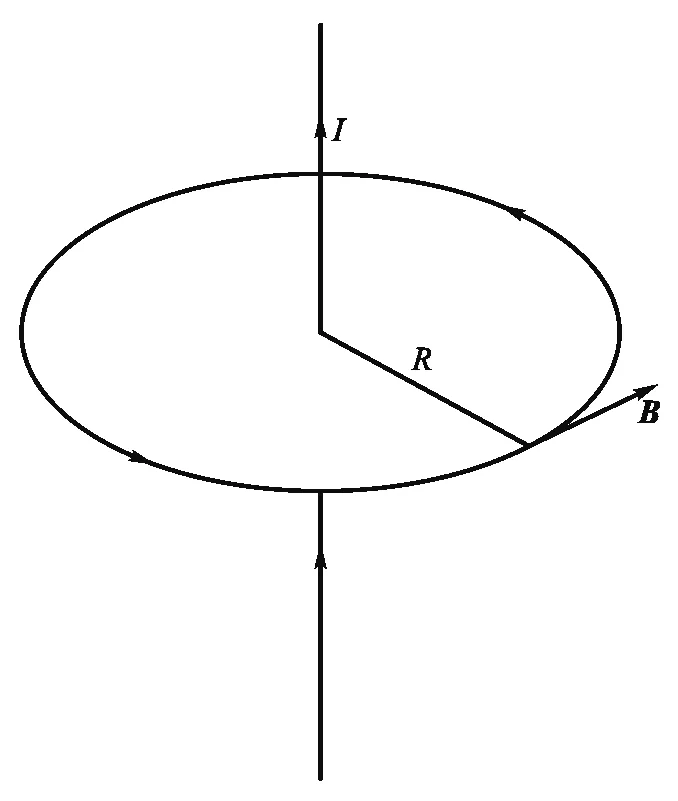
图1 无限长载流直导线磁感应强度分布示意图

值得注意的是，安培环路定理的应用，要求电流体系的对称性非常高，这也是大家在应用安培环路定理时容易忽视的一个问题.如果电流体系的对称性不满足要求，磁感应强度分布的对称性也会受到相的破坏，此时的路径积分不能轻易简化，即式(2)不再成立.

以柱对称载流体系为例，当该体系不满足无限长要求时，尽管磁感应强度分布还是柱对称的，但沿轴方向的平移对称性已经被破坏，端面处的磁感应强度与中截面处的磁感应强度有着较大区别，直接利用式(2)计算端面处的磁感应强度分布已经不够准确.只有中截面处且回路半径R远小于柱长度时，才能够利用式(2)较为准确的得到磁感应强度的大小，因为此时的柱对称载流体系相对于回路的结构可以近似地看作无限长.

但并不意味着安培环路定理在端面处不成立，安培环路定理对于任意电流体系都是成立的[8,9].应用安培环路定理时，需要具有特殊对称性的电流体系.这是因为一般的电流体系中，路径积分比较困难，而特殊对称性的电流体系中，路径积分可简化.

2 有限长载流直导线中的安培环路定理

对于有限长载流直导线体系，常有学生认为其不满足安培环路定理.如图2所示，根据毕奥-萨伐尔定理，可得到有限长载流直导线产生的磁感应强度的大小的分布为

(5)

其中，R为场点到载流直导线的垂直距离，θ1和θ2分别为场点与载流直导线两个端点的连线和电流方向的夹角，磁感应强度的方向由电流方向的右手螺旋关系得到.选择以导线为轴，半径为R的圆形回路，回路的正方向与磁感应线的方向相同，磁感应强度沿该回路的路径积分为

(6)

该回路积分的值和回路所包围的电流与真空的磁导率的乘积μ0I不相等，导致了很多学生认为安培环路定理此时不成立.

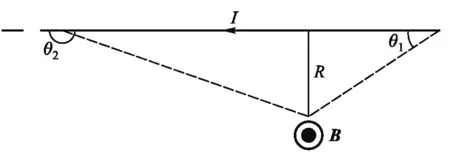
图2 有限长载流直导线的磁感应强度分布示意图

产生该误解的原因是，实际情况中电流不能凭空产生，也不能凭空消失，只能存在于一个闭合电路中[10-12].例如无限长载流直导线，是电路中存在一根较长的直导线且积分回路在直导线中点附近，回路半径远小于直导线长度时的一种近似的理想模型.此时电路中的其他载流导线与积分回路的距离足够远，在回路上产生的磁感应强度B2相对于该直导线在回路上产生的磁感应强度B1可忽略不计.

因此，对于有限长载流直导线体系，可以将其置入一个闭合电路中进行讨论.但是，除该直导线在回路上产生的磁感应强度B1外，电路中其他载流导线在回路上产生的磁感应强度B2不能忽略.可以利用图3所示的电路对有限长载流直导线体系的安培环路定理进行探讨.回路包含两根正交的直导线L1和L2，积分回路是以直导线L1为轴且半径为R的圆，与直导线L2的垂直距离为a.除两根直导线外，电路中其他载流导线与回路的距离足够远，在回路上产生的磁感应强度可以忽略不计.载流导线L1和L2在回路上产生的磁感应强度分别为B1和B2.根据磁场的叠加原理可知回路上的磁感应强度为

B=B1+B2

(7)

总磁感应强度在该回路上的路径积分为

∮lB·dl=∮lB1·dl+∮lB2·dl

(8)

且磁感应强度B1的路径积分为

(9)

其中，θ为回路上任意一点与两直导线交点的连线l和直导线L1的夹角.

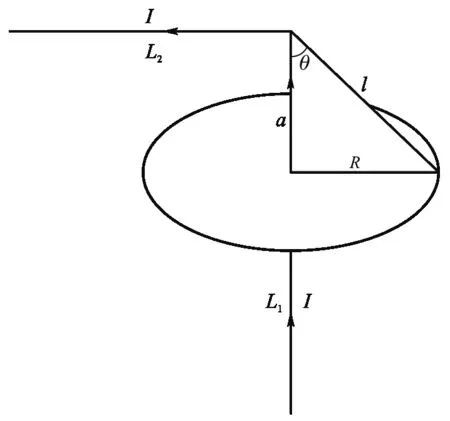
图3 有限长载流直导线的电路构造示意图

对于磁感应强度B2，如图 4(a)所示，以回路的圆心为坐标原点O，直导线L2在回路平面上的投影的反方向为x轴，直导线L1的方向为z轴建立三维直角坐标系.根据毕奥-萨伐尔定理，回路上任意一点N处的磁感应强度B2的方向应当垂直于直导线L2和MN构成的平面，其中MN为一条平行于x轴的直线.如图4(b)所示，直导线L2在回路上N点处产生的磁感应强度的大小为

(10)

其中，r为N点到直导线L2的垂直距离(线段AM的长度)，l为N点到导线端点A的距离，ψ为N点与导线端点的连线和直导线的夹角，φ为N点与圆心O的连线和x轴的夹角，即

(11)

(12)

(13)

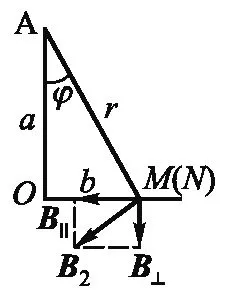
如图4(c)所示，磁感应强度B2不在回路构成的平面内，可以将其分解为回路平面上的分量B∥和垂直于回路平面的分量B⊥，其中

(14)

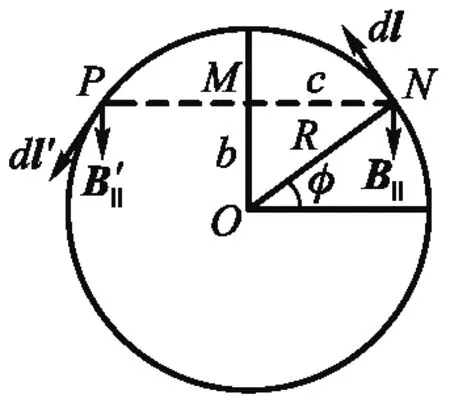
如图4(d)所示，磁感应强度B2在N点处的路径积分的微元为

(15)

P点处的路径积分微元为

(16)

磁感应强度B2该回路上的路径积分为

(17)

被积函数是偶函数，因此

(18)

可以利用x=tanφ替代积分变量的方法得到上述积分运算的结果.总磁感应强度B在该回路上的路径积分为

(19)

可见，安培环路定理在有限长载流直导线体系中仍然是成立的.

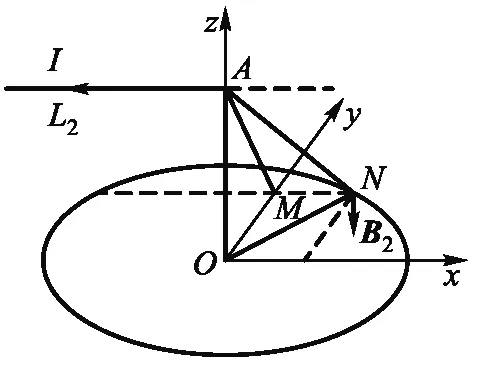
(a) 3维视图

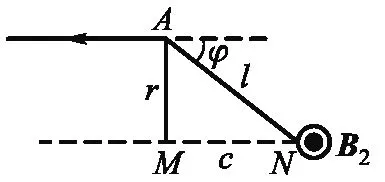
(b) AMN平面视图

(c) yz平面视图

(d) xy平面视图

3 结论

安培环路定理是稳恒磁场中的一个重要定理，具有很强的物理意义和应用价值. 但是，根据本人多年的教学经验，发现学生在学习过程对安培环路定理的理解不够，特别是对其应用的条件和普适性容易混淆. 本文首先介绍了安培环路定理的应用条件：当电流体系具有特殊高对称性时，其环路积分可以大大简化，因而计算非常方便；当电流体系的对称性受到破坏时，环路积分的简化不再成立. 但是安培环路定理是普遍成立的. 通过有线长载流直导线的例子，澄清了安培环路定理此时不成立的误解. 采用简单的电路构造法，避免了相对复杂矢量和矢势运算，更容易让学生、特别是非物理专业的学生接受，能够帮助学生更好地掌握安培环路定理和进一步理解磁场的性质.