基于永磁差动的桁架式高频力马达力-位移特性仿真分析

卢 仪，孟 彬，戴铭柱

(浙江工业大学 机械工程学院，浙江 杭州 310023)

引言

电液伺服阀是电液伺服控制系统的核心部件，由于具有精度高、响应快、功率大等诸多优点，广泛应用于航空航天、船舶、冶金、国防工业等领域。而电-机械转换器作为电液伺服阀的驱动元件，决定了阀的滞环、频响等重要指标，是影响电液伺服阀性能优劣的关键之一[1-3]。

常见的直动式电-机械转换器有比例电磁铁和力马达等，而高频响正是发展方向之一。比例电磁铁由于自身精度低、体积大、频率响应慢，且只能提供单向的驱动力，往往难以胜任需要快速响应的场合。力马达由于体积小、驱动力大，在直动式电液伺服阀上广泛应用。MOOG公司开发的用于D633/D634直动式电液伺服阀的永磁极化式双向线性力马达，采用双磁钢单线圈的结构，利用线圈控制磁通和永磁极化磁通的差动驱动方式，实现双向控制，频响相比比例电磁铁有较大提升[4-5]。本研究提出一种基于永磁差动的桁架式高频力马达，利用差动驱动控制和桁架式的新结构，实现力马达双向高频控制[6-7]。

1 工作原理

桁架式高频力马达的结构如图1所示，主要由轭铁、衔铁、永磁体、控制线圈和推杆5部分组成。控制线圈产生的磁通通过轭铁的桁架式结构传输到两臂；2块相同的衔铁对位交错，将2片永磁体和推杆夹在中间，组成衔铁部件；线圈和永磁体产生的磁通通过4个工作气隙，形成永磁差动的特殊磁路。

桁架式高频力马达工作原理如图2所示，令此时衔铁部件所在位置为初始位置，2块永磁体N极如图1b所示同向布置，使得衔铁部件4个工作气隙面的对角极性相同，产生永磁极化磁通φg。当控制线圈通入如图2所示的电流时，产生电流控制磁通φc，电流控制磁通φc与永磁极化磁通φg在工作气隙δ1,δ2,δ3,δ4内相互叠加，其中在工作气隙δ1,δ2内的电流控制磁通与永磁极化磁通方向相反，磁通强度减弱，电磁吸力减小；在工作气隙δ3,δ4内的电流控制磁通与永磁极化磁通方向相同，磁通强度增强，电磁吸力增大；此时衔铁部件受到轴向向下的推力，产生如图2所示方向的位移x。

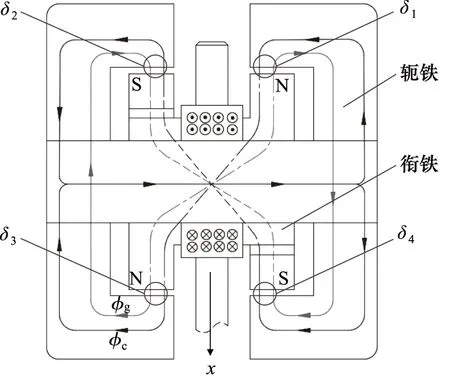
图2 桁架式高频力马达磁路示意图

随着推力产生的位移逐渐增大，推力与复位弹簧弹力的合力逐渐减小为0 N，衔铁部件就能达到新的位置平衡。当控制线圈断电时，在此时工作气隙δ1,δ2，δ3，δ4内的电流控制磁通消失，衔铁部件所受的推力消失，在复位弹簧的作用下，衔铁部件又回到初始位置；当控制线圈通入相反的电流时，衔铁部件受到轴向向上的推力，向相反位置移动。

在材料上，永磁体选用钕铁硼NdFeB，相比铁氧体和铝镍钴磁铁，具有更大的磁能积；轭铁和衔铁选用电工纯铁DT4，其磁导率高，磁滞特性不显著，剩磁易消除，且在交变磁场中磁滞损耗小，是理想的软磁材料[8]。

轭铁的桁架式结构确保了力马达磁路对称，使控制线圈到4个工作气隙路径相等，轴向两侧的工作气隙能获得相同的控制线圈提供的磁通，无论衔铁往轴向任一方向位移，都能输出相同的力，确保换向后不改变性能。

由于采用永磁差动的方式，充分利用磁路，精简了衔铁部件的结构，保证了输出的功率，同时，紧凑的衔铁部件结构使其体积和质量能保持在较小的水平，在不变更衔铁部件材料的情况下，减小质量能有效提高频率，确保该力马达理论上能实现高频响。

2 数学模型

2.1 磁场分析

在电磁场中，基本规律由麦克斯韦方程组高度概括和总结，可用于宏观电磁场模型的分析，是有限元仿真的基础。麦克斯韦方程组可细分为4个基本定理：安培环路定理、法拉第电磁感应定理、高斯磁通定理以及高斯电通定理。麦克斯韦方程组相应微分形式如式(1):

(1)

式中，H—— 磁场强度矢量，T

J—— 传导电流密度矢量，A/m2

D—— 电通密度矢量，C/m2

E—— 电场强度矢量，V/m

B—— 磁感应强度矢量，T

ρ—— 电荷体密度，C/m2

3 仿真结果及分析

传统的方法诸如经验公式法、磁路分割法，虽然计算简便，但是求解过于理想化，精度远不如有限元法。有限元法通过对整个求解区域分解，用偏微分方程边值问题求近似解，即使结构再复杂，有限元法依旧能得出较精准的结果，但是计算量极大，因此，运用计算机软件求解是较合理的方式。Ansoft公司开发的Maxwell软件基于有限元法和麦克斯韦方程组，能分析各种静态电磁场、涡流和瞬态电磁场，自带自适应网格剖分和强大的后处理功能，使其成为行业应用广泛的三维电磁设计软件[9-11]。

对该力马达进行几何建模，导入Maxwell 3D，定义各部件材料，设置边界条件和激励源，选择受力分析对象，进行有限元网格剖分，设置参数和分析步骤，最后求解，得到数据并后处理[12-13]，仿真模型参数数据见表1。

表1 力马达仿真模型参数

3.1 控制电流对力-位移特性曲线的影响

改变控制线圈电流大小，分别通入1, 2, 3, 4 A的电流，仿真结果如图3、图4所示。

在图3中，可以明显看到磁场磁通在单侧叠加，且随电流增大，加强逐渐明显。在图4力-位移特性曲线中，横坐标代表衔铁部件的位移x，纵坐标代表衔铁部件受到的力F，更大的力意味着电-机械转换器能达到更高的精度和稳定性[14-15]。随着控制线圈电流不断增大，力也在不断增大。在位移1.6 mm、线圈电流分别是1, 2, 3, 4 A时得到的力的大小依次为21.9, 25.6, 29.3, 32.6 N，力的大小与控制线圈电流大小近似呈线性相关。保证发热维持在正常情况下，尽可能地增加线圈匝数和增大电流，能有效改善力-位移特性。

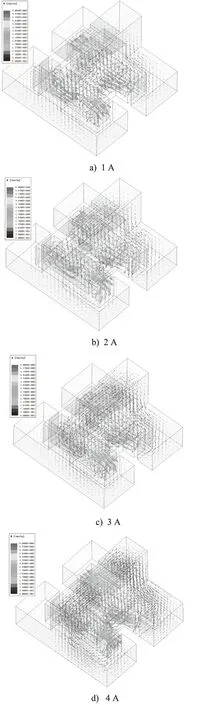
图3 不同电流下的力马达初始位置磁场分布

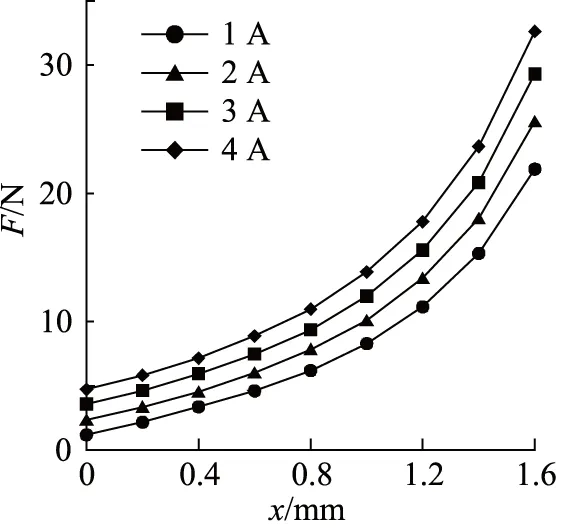
图4 不同电流下的力-位移特性曲线

3.2 永磁体高度对力-位移特性曲线的影响

改变永磁体高度为1, 3, 5, 7 mm，仿真结果如图

5所示。永磁体高度为1 mm和7 mm时力-位移特性曲线基本相同，在位移1.6 mm处分别得到22.4 N和21.2 N的力；永磁体高度为3 mm和5 mm时力-位移特性曲线基本相同，在位移1.6 mm处分别得到26.8 N 和25.6 N的力。

图5 不同永磁体高度下的力-位移特性曲线

改变永磁体高度即改变永磁体体积，过小的永磁体无法保证产生足够的极化磁通，导致输出的力降低；而永磁体体积过大时，可能产生严重的漏磁，影响磁路，并且过大的永磁体占用了衔铁的空间，导致衔铁厚度不足，造成磁饱和，降低了输出的力。永磁体应选择适宜的高度，若输出力-位移特性曲线相近，可选择较低的永磁体高度以减少加工成本。

3.3 气隙面积对力-位移特性曲线的影响

改变工作气隙面积为65, 91, 117 mm2，仿真结果如图6所示。在位移1.6 mm处，分别得到17.9，25.6，32.6 N的力。可以看到，随着气隙面积增大，相应的力也在不断增大，力的大小与气隙面积近似呈线性相关。在考虑力马达结构合理的基础上，气隙面积应尽可能增大。

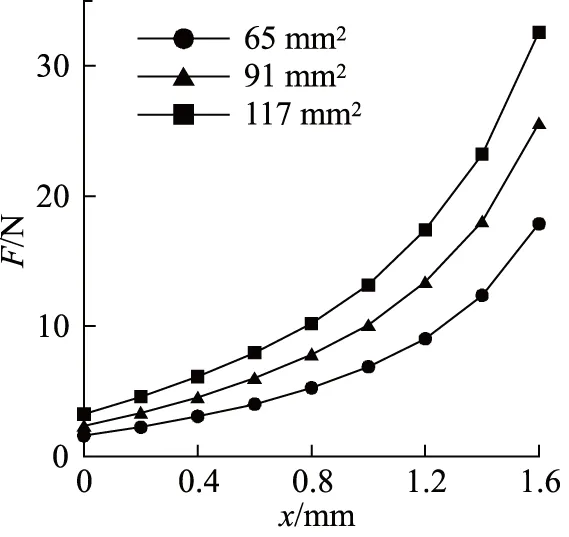
图6 不同气隙面积下的力-位移特性曲线

3.4 初始气隙距离对力-位移特性曲线的影响

改变初始气隙距离为2.0, 1.4，0.8 mm，仿真结果如图7所示。为了防止衔铁和轭铁距离过近发生贴合，需要空余一段距离作为非工作行程，以保证力马达正常工作。图中，横坐标代表剩余气隙距离，非工作行程定在剩余0.4 mm范围。

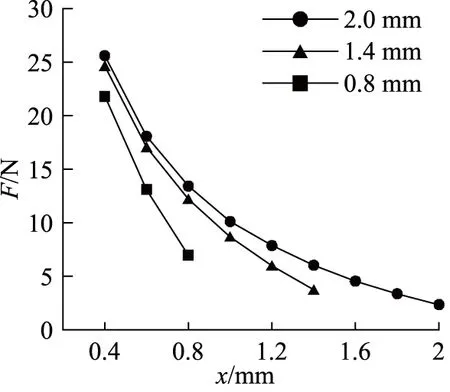
图7 不同初始气隙距离下的力-位移特性曲线

由于存在非工作行程，改变初始气隙距离为2.0, 1.4, 0.8 mm，意味着单向工作行程分别为1.6, 1.0，0.4 mm。可以看到，剩余气隙距离0.4 mm处，初始气隙2.0, 1.4, 0.8 mm分别得到25.6, 24.6, 21.8 N的力。这是由于初始气隙缩短后，对于衔铁工作行进方向相反的一侧气隙来说气隙距离也是减小的，即使叠加磁通削弱，依旧能输出更大的反力，导致合力减小。因此，该力马达应尽可能选择大行程。

4 结论

(1) 针对传统力马达及比例电磁铁频响低的特点，提出一种基于永磁差动的桁架式高频力马达，该力马达运用永磁体和线圈差动控制的原理实现双向高频控制;

(2) 利用Ansoft仿真软件来分析力马达的力-位移特性，仿真结果表明，该力马达结构合理，在位移1.6 mm处能输出25.6 N的力；对其进行增大控制线圈安匝数、选择高度适中的永磁体、增大气隙面积以及选择大行程的设计优化，能有效增加输出的力，获得更佳性能。