基于高斯过程的阀控非对称液压缸模型预测控制
2021-08-18陶建峰余宏淦刘成良
孙 浩,陶建峰,余宏淦,刘成良
(上海交通大学 机械与动力工程学院,上海 200240)
引言
阀控非对称液压缸系统具有结构紧凑、空间布置灵活、功率密度大等特点,广泛应用于工程车辆、加载试验台、机械臂等设备,多采用比例/伺服阀作为控制元件,实现闭环力/位置/速度控制。控制阀的非线性、液压缸的不对称性及负载扰动等强非线性因素会造成系统响应滞后、输出超调、运动不平稳等,如何从控制方面解决上述问题是众多学者研究的方向[1-3]。
丁问司等[4]采用粒子群优化算法实现模糊控制参数寻优,在线调整PID参数,有效抑制了油液含气量的增加对位控系统动态特性的影响,但并未解决超调问题;LINJAMA M等[5]设计了基于模型的串级PID控制器,避免了因负载质量和体积模量造成的延迟特性,实现了精确的力/位置控制;JIANPENG S等[6]为实现挖掘机动臂平稳运行和精确位控,提出了基于模式切换的速度和位置组合控制策略,在能量损耗、动态特性和抗负载扰动方面均取得了很好的效果;KIM K等[7]以动臂速度场为优化目标,考虑泵流量约束,实现了变工况下速度的最优控制;HAO Y等[8]采用滑膜控制实现了位控系统的轨迹跟踪控制,在有限时间内保证了误差的收敛性,局限于无负载扰动工况;金坤善等[9]采用扩张观测器实时估计综合扰动和状态,提出了一种二阶线性自抗扰策略,可以有效抑制不确定性扰动对控制系统的影响;何常玉等[10]利用动态面方法,并引入一阶滤波器设计控制器,解决了反步法的复杂爆炸问题,提高了系统的位置精度和鲁棒性。与采用普通PID相比,上述研究在相应工况下,均实现了很好的控制效果,提高了系统的控制精度和鲁棒性,但当系统在满足快速性或负载发生变化时,输出会伴有超调现象,导致阀芯在零位附近切换,由于非对称液压缸伸出和缩回工况的动态特性不同,控制效果则会变差。模型预测控制由于可以处理复杂约束条件,是解决上述问题的有效控制方法。熊志林等[11]采用状态估计设计了模型预测控制器,使用卡尔曼滤波器减小实际系统噪声对状态估计的影响,根据物理方程建立了线性预测模型,为消除其与实际模型间的误差,引入了积分行为。由于阀控非对称缸系统非线性问题突出,采用线性模型会存在一定局限性,而机器学习方法具有处理非线性问题的能力,可以很好的应用于复杂建模方面。杨泰春等[12]采用支持向量回归辨识系统非线性模型,进一步提高了预测模型的精度,减少了系统的稳态误差,但局限在于未考虑实际采集信号混有噪声的影响,超参数需调试确定,预测模型的输出值无法解释。高斯过程回归与支持向量回归相比,优势在于考虑了混有噪声的训练集样本,超参数可自适应获取,预测的输出值具有概率意义,所需样本数量少[13]。
本研究首先介绍了液压系统和模型预测控制器的原理,推导了高斯过程回归建模、核函数及超参数选择过程;然后,以建立的非线性仿真模型为研究对象,进行模型预测控制器的设计,根据核函数和训练集数据确定了超参数,采用高斯过程回归训练得到了非线性离散数学模型;最后,仿真分析了高斯过程回归训练模型的精度和模型预测控制器的控制效果。
1 液压系统及控制器介绍
1.1 液压系统工作原理
本研究的液压系统适用于装配用机械臂的驱动关节,定位精度需满足±0.1 mm。部分液压系统原理如图1所示,由电液伺服阀1、溢流阀2(安全阀)、液压缸3(带磁致伸缩位移传感器)、锁紧阀4(到达目标位置通电即锁紧液压缸)、压力传感器5、位移传感器6组成。油源为恒压变量泵,伺服阀开口和液压缸承受的负载决定了液压泵的输出流量。伺服阀的指令信号为-10~10 V,阀芯位移与其成正比,在指令信号为10 V 时,阀芯位于阀口P至A和B至T全开(100%)位置,液压油流入无杆腔,活塞伸出,另一侧同理。控制器根据采集到的位置信号和期望的输入信号,计算输出信号作用于伺服阀,以实现对系统的位置控制。
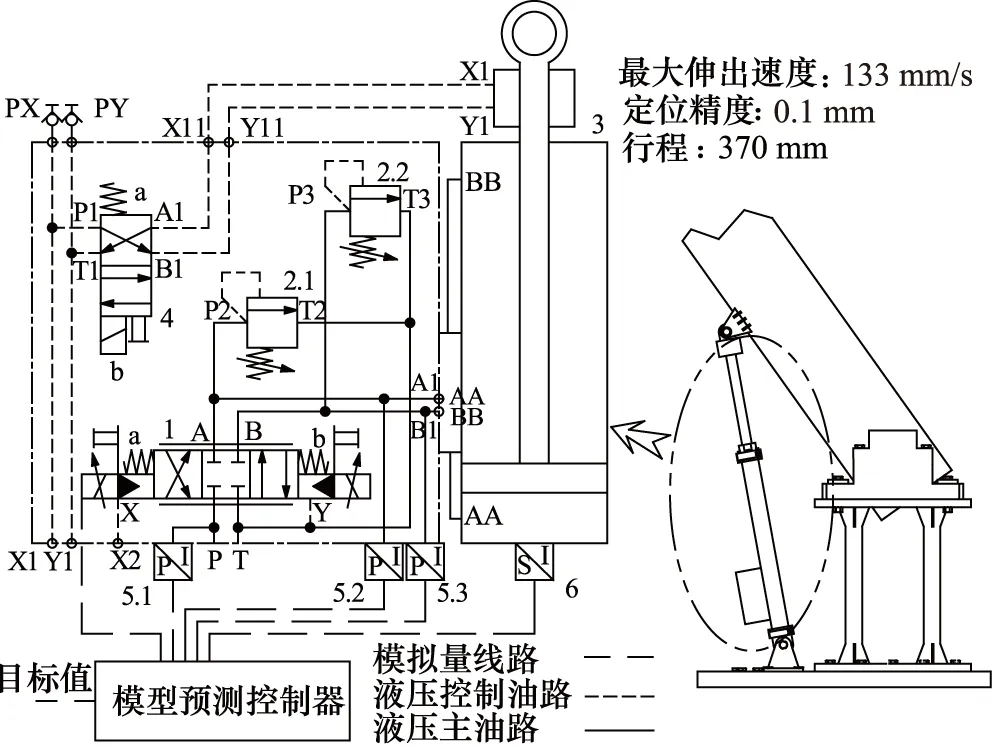
1.电液伺服阀 2.溢流阀 3.液压缸 4.锁紧阀5.压力传感器 6.位移传感器图1 液压系统原理图
当液压缸输出存在超调时,即使在稳态时达到定位精度要求,但在动态调整过程中会损坏具有配合要求的安装面,这在实际中是不允许的。因此,采用模型预测控制建立液压缸位置不超过期望值和伺服阀阀芯始终在单边工作的约束,可以解决阀控非对称缸系统输出超调和控制效果变差的问题。
1.2 模型预测控制器原理
模型预测控制器是基于预测模型设计的,本质为求解多约束条件下二次规划问题的过程,结构如图2所示,需建立离散数学模型,根据当前时刻实际系统位置输出和下一时刻伺服阀指令电压(模型预测控制器输出)及负载力,得到下一时刻预测模型位置输出,为减小预测模型与实际系统的误差,采用机器学习中的高斯过程回归辨识实际系统非线性模型,将其作为非线性等式约束;保证伺服阀指令电压范围为-10~10 V,预测模型位置输出不超过期望位置输入,分别将其作为线性不等式约束;未来有限时刻预测模型位置输出需高精度跟踪期望位置输入,伺服阀指令电压不能变化过快,以此建立二次型优化目标函数,采用最优化方法在有限时域范围内不断滚动求解,将每次计算出的第一个最优指令电压值输出给实际系统。
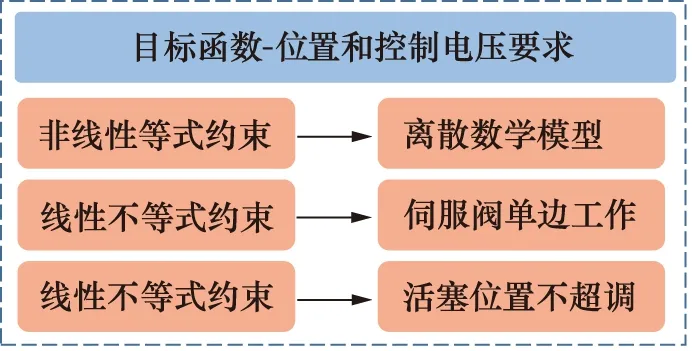
图2 模型预测控制器结构
2 高斯过程回归建模
高斯过程回归是以贝叶斯理论为基础的机器学习方法,目的是求出预测输出值的后验概率分布,根据其均值和方差可以得到具有置信区间的预测输出结果。
2.1 高斯过程回归推导
阀控非对称缸系统输入与输出的关系是非线性的,可以选择合适的非线性变换将该系统的输入特征映射到高维空间,使其在高维空间中变为线性可分的问题,n维输入xl=[xl,1,…,xl,u,…,xl,n]T单输出的非线性函数f(xl),可以在高维空间中线性表示为:
f(xl)=qTw=μ(xl)Tw
(1)
式中,μ即为非线性变换,q=μ(xl)为变换后映射到m维空间后的向量(m≫n),w为权重向量,w∈Rm,xl,u为u特征下的值。
实际在处理回归问题时,需考虑训练集中输出值存在的噪声,实际输出值可以表示为:
y=f(xl)+λ=μ(xl)Tw+λ
(2)
式中,λ表示训练集中输出值混有的噪声项,假设其服从N(0,σ2)。
该非线性回归问题需根据采集的数据(训练集)得到权重向量。根据式(2)及噪声λ分布可以写出输出样本条件概率密度函数:
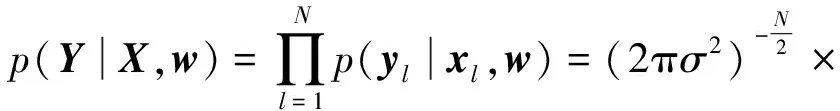
(3)
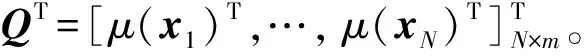
权重向量w存在先验分布,假设其服从均值向量为0,协方差矩阵为G的多元高斯分布,则:
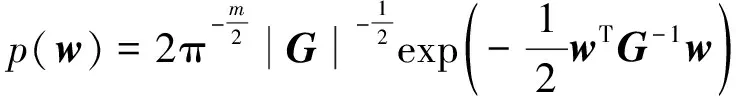
(4)
权重向量w的后验概率分布为:
(5)
式中,p(Y|X)为边缘概率密度。
式(5)可以由式(3)和式(4)表示为:
p(w|X,Y)∝p(Y|X,w)p(w)
(6)
式中,w′=σ-2(σ-2QQT+G-1)QY。
可知权重向量w的后验概率分布服从均值为w′,协方差矩阵为L-1的多元高斯分布:
p(w|X,Y)~N(w′,L-1)
(7)
其中:
L=σ-2QQT+G-1
(8)
当有测试集输入时,可以使用式(7)进行回归预测,规定测试集原始n维输入为x*,经非线性变换后为q*=μ(x*),则预测输出y*的概率分布为:
(9)
整理得预测输出y*的概率分布服从:
N(σ-2μ(x*)TL-1QY,μ(x*)TL-1μ(x*))
(10)
根据式(8),L逆矩阵可整理为:
L-1=G-GQ(σ2E+QTGQ)-1QTG
(11)
令K=QTGQ,k(x*,x*)=μ(x*)TGμ(x*),k(x*,X)=μ(x*)TGQ,k(X,x*)=QTGμ(x*),将式(11)带入式(10)中,整理得:
σ-2μ(x*)TL-1QY=k(x*,X)(σ2E+K)-1Y
(12)
μ(x*)TL-1μ(x*)=k(x*,x*)-
k(x*,X)(σ2E+K)-1k(X,x*)
(13)
上述K,k(x*,x*),k(x*,X),k(X,x*)项是以非线性映射函数μ(x)的内积形式表示,可定义为核函数。
2.2 核函数及超参数确定
核函数可以将高维特征空间中的向量内积运算转化为原始低维空间中的函数计算,极大的降低计算量。选择合适的核函数,根据给定的训练数据按概率估计最优超参数后,2.1节中所述的高斯回归过程便可用于训练模型并进行预测,其中,估计最优超参数的过程为求解无约束多变量极值问题。
本研究选择最常用的高斯径向基核函数:
式中,xa和xb表示原始空间n维输入向量;γ2表示高斯核函数幅值;α表示特征长度尺度,对所有基函数的作用效果均相同。
高斯核函数可写成如下形式:
式中,xa,u和xb,u分别表示对应的第u维分量。
模型超参数集合表示为Ω=[γ,α,σ]T,可采用极大似然法,求取似然函数极值来估计超参数。根据式(2)、噪声λ和权重向量w分布可以写出向量Y服从N([0]N×1,[K(X,X)+σ2E]N×N)。以训练集输出值的边缘分布函数的负对数作为似然函数:
L(γ,α,σ|X,Y)=-ln(P(Y|X))=ξ(γ,α,σ)
(16)
将求解概率乘积的极大值转化为求解无约束多变量极小值问题。
3 模型预测控制器设计
阀控非对称缸系统的模型预测控制器原理如图3所示。该控制器是以辨识的高斯过程回归模型为基础,通过求解二次规划问题,得出最优控制值作用于系统。
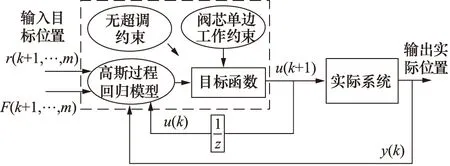
图3 模型预测控制器原理
3.1 高斯过程回归模型辨识与预测
定义当前时刻为k,下一时刻为(k+1),非对称阀控缸系统的离散数学模型为:
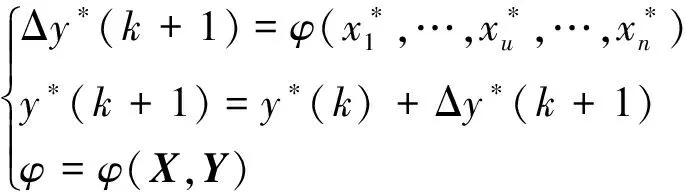
(17)
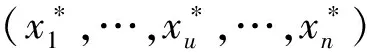
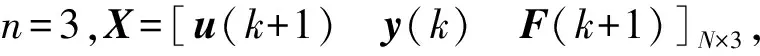
首先选择高斯径向基核函数,根据训练集输入和输出样本,建立输出样本Y的似然函数式(16),采用最速下降法求解损失函数的极小值,得到超参数Ω=[γ,α,σ]T,最优超参数值随训练集样本数量的改变自适应变化。
然后,计算训练集的核矩阵:
当输入测试集x*时,与训练集样本点的核向量为:
k(x*,X)=k(X,x*)T=[k(x*,x1)…k(x*,xN)]
(19)
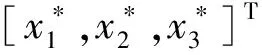
3.2 二次规划问题构建
1) 目标函数
本研究的非对称阀控缸系统需实现精确的位置控制,同时需保证控制器输出的电压值变换平稳,目标函数可以用以下二次型表示:
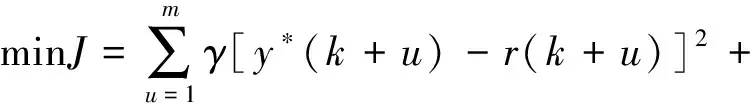
(19)
式中,γ,ρ分别为位置权重和控制权重;y*(k+u)为(k+u)时刻预测位置输出值;r(k+u)为对应时刻位置参考值;u(k+u)为(k+u)时刻电压值;u(k)为k时刻电压值;m,n分别为位置时域长度和控制值时域长度。
2) 约束
考虑液压缸在任意位置运动,建立无超调输出约束:
(20)
为实现伺服阀阀芯在工作时不换向,建立输入约束:
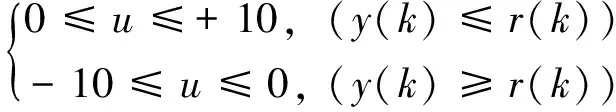
(21)
综上所述,根据优化目标函数式(19),考虑线性不等式约束式(20)和式(21),非线性等式约束式(17),采用序列二次规划方法求解二次规划问题,[y*(k+1),…,y*(k+m),u(k+1),…,u(k+n)]T为最优解,以第一个控制值u(k+1)作为控制器输出。
4 仿真验证
本研究仅进行仿真验证,采用文献[14]的阀控非对称缸系统的状态方程,选择零开口伺服阀,视其为二阶振荡环节,忽略恒压变量泵的动态特性,建立输入为控制电压和外负载力、输出为活塞位置并混有高斯白噪声的连续时间非线性数学模型。从该模型中采集训练集和测试集样本,并验证控制器效果。以活塞伸出工况为例,相关技术参数如表1所示,其他仿真参数见表2。
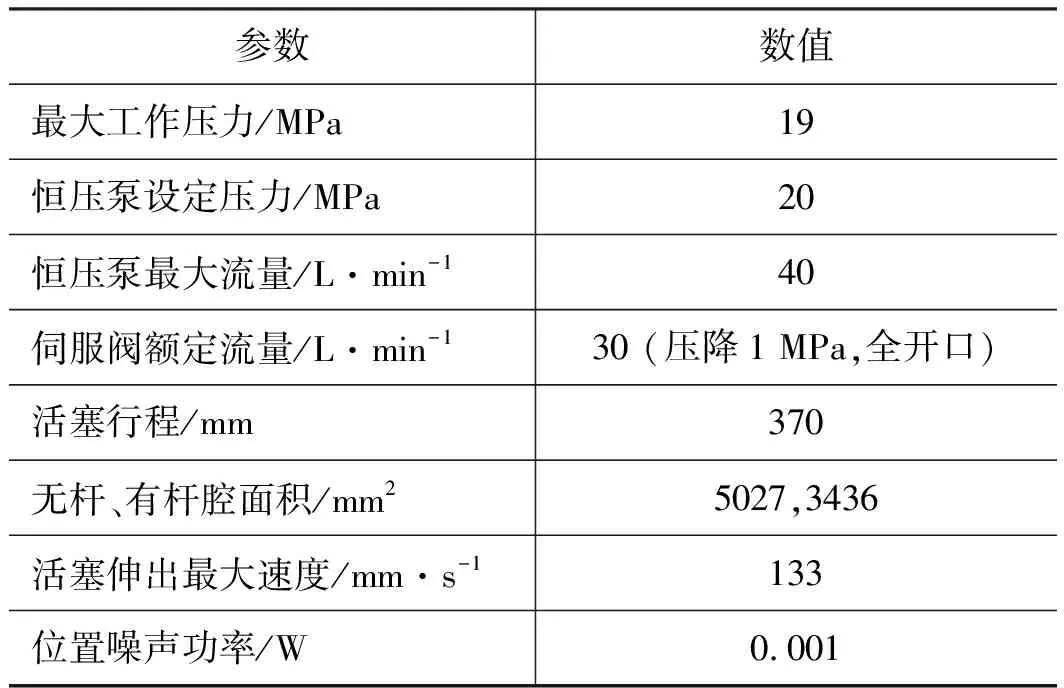
表1 相关技术参数
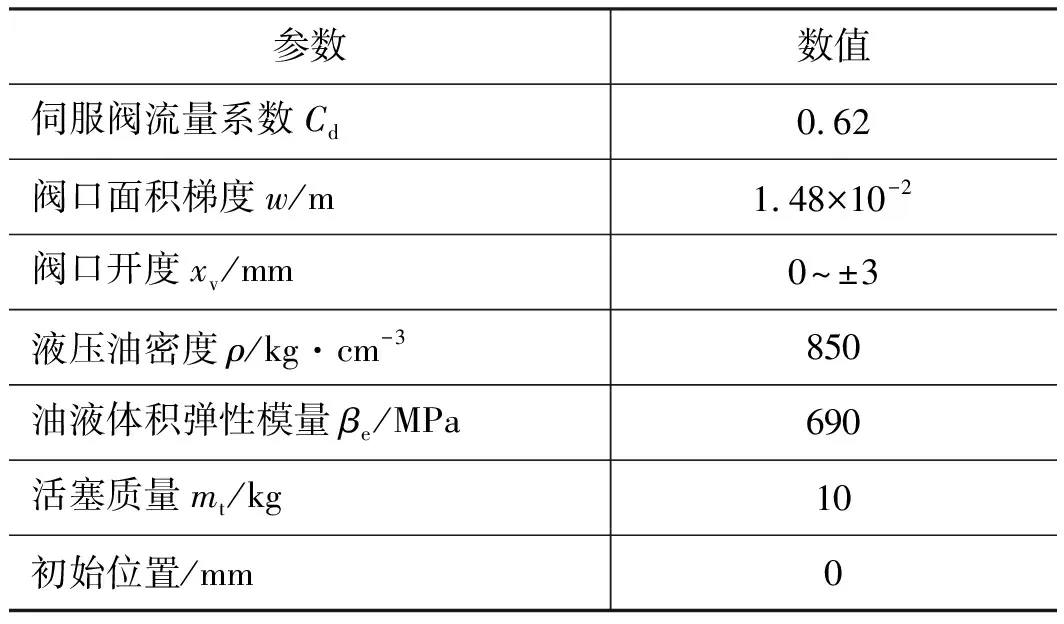
表2 阀控非对称缸系统模型参数
4.1 高斯过程回归模型精度验证
采集阀控非对称缸系统数学模型时域范围阶跃响
应数据,输入电压0~10 V,间隔1 V,输入负载0~90 kN,间隔10 kN,输出位置0~370 mm,时间间隔0.05 s。将上述数据离散化处理,得到训练集样本,由于输入特征量纲不同,数值间差别过大,为提高模型训练精度,对输入特征进行零均值规范化处理,处理后的特征数据均值为0,方差为1,归一化后的训练集输入样本为:
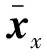
根据2.2中选择的高斯径向基核函数,及上述归一化后的训练集数据,便可进行超参数寻优,设置初始值Ω0=[0,0,-1]T,得到最优超参数为Ω=[2.259,0.754,0.710]T,进而训练模型。为验证模型的泛化能力,随机选择测试集工况如表3所示,得到预测输出曲线如图4~图7所示。
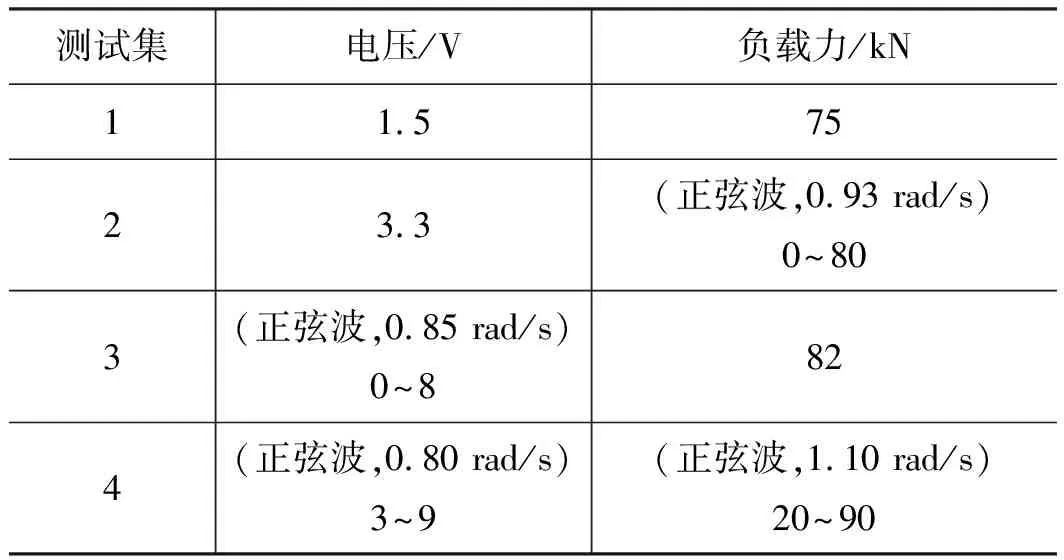
表3 测试集输入参数
从图4~图7计算出测试集输出的均方误差、输出噪声的实际标准差,如表4所示。
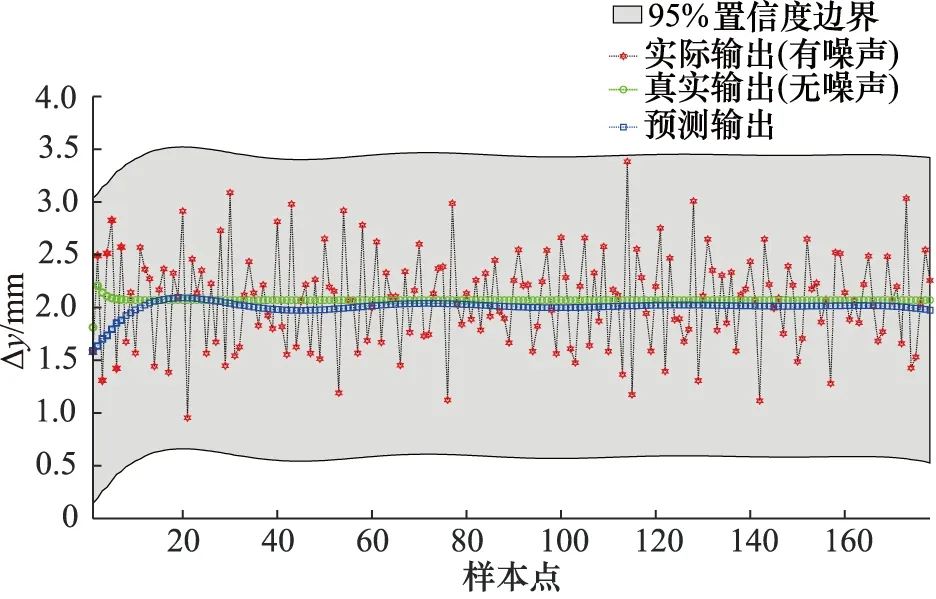
图4 测试集1预测输出(位移增量)曲线

图5 测试集2预测输出(位移增量)曲线
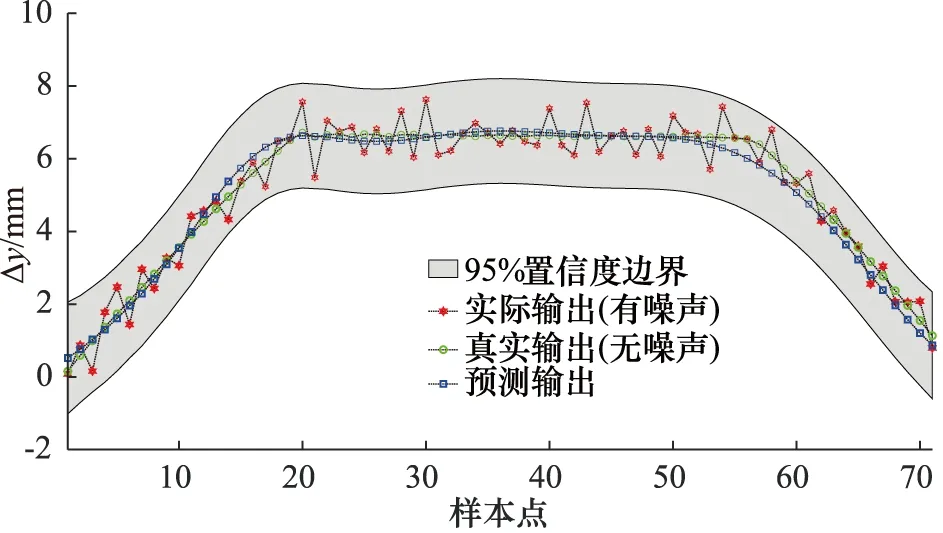
图6 测试集3预测输出(位移增量)曲线
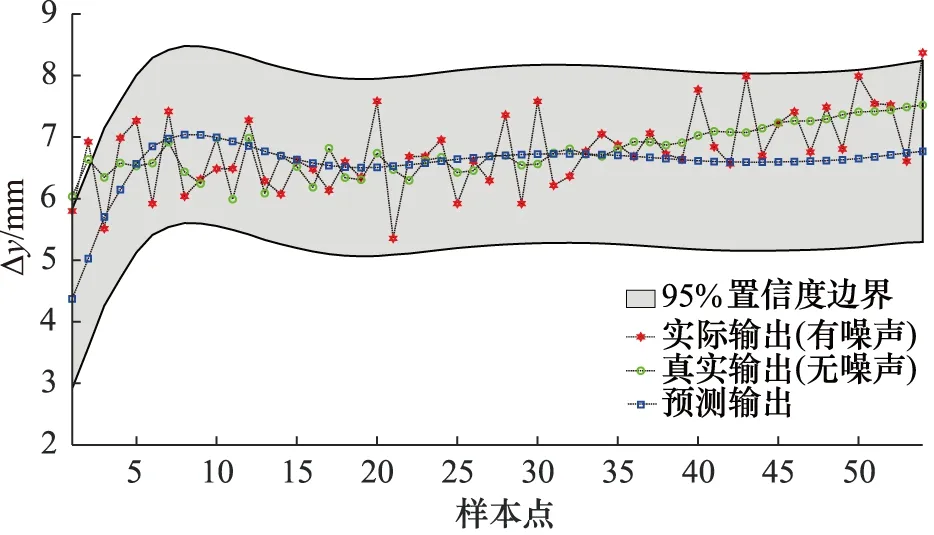
图7 测试集4预测输出(位移增量)曲线
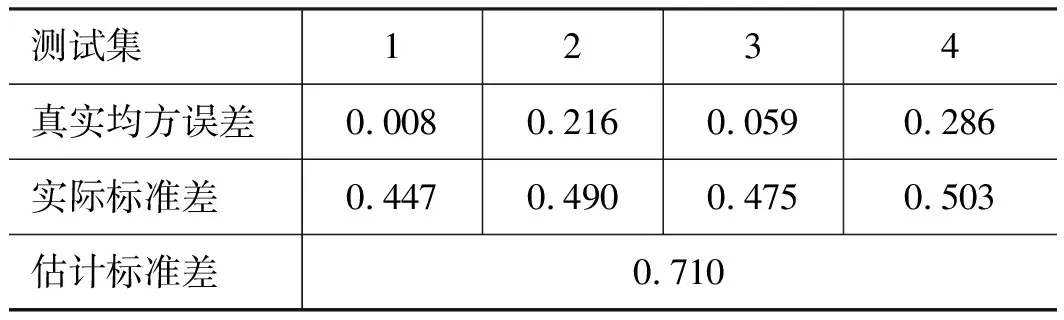
表4 4类测试集预测输出结果
采用高斯过程回归训练模型,可以得到预测输出值的置信区间,超参数根据核函数和训练集自适应获取,样本集允许存在噪声,对预测输出的噪声有很好的估计,训练后的离散模型能精确的预测非对称阀控缸系统真实输出,并具有很强的泛化能力,可以用作模型预测控制中的非线性等式约束。
4.2 模型预测控制算法验证
模型预测控制器实质是求解二次规划问题,设置3.2.1节中目标函数的位置参考值为160 mm,初始电压为0 V,位置时域长度m=10,控制值时域长度n=5,位置权重和控制权重的取值直接影响寻优速度,取γ=10,ρ=1;不等式约束需满足3.2.2节中要求;3.1节中非线性等式约束初始位置为0 mm,训练集样本的均值和标准差分别为:
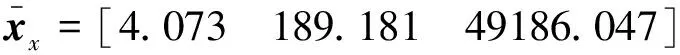
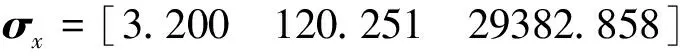
(23)
采用序列二次规划算法求解上述二次规划问题。仿真中设置控制器时间间隔为0.05 s。
为对比所提控制算法与PID控制在系统满足快速性或负载发生变化条件下的控制效果,设置工况条件及对应PID参数如表5所示。
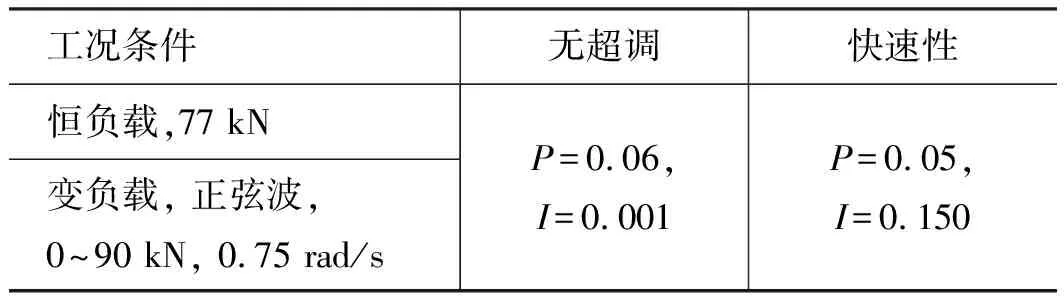
表5 两种工况条件及PID参数
恒负载和变负载工况下预测控制和PID控制位置变化如图8和图10所示,对应控制电压变化如图9和图11所示,稳态误差如图12和图13所示。
从图8和图10中可以得出两种工况下,稳态时真实位置均方误差如表5所示。
从图8~图11可以得出,当采用PID控制时,为实现快速性,输出必存在超调,控制值的变化会导致伺服阀不断换向,为实现无超调,控制值虽平稳变化,但同样需要一定的时间才到达稳态。从表4和表5中数据可知,同一组PID参数在变负载工况下,稳态输出超调现象加剧,应对变负载工况存在局限性;为实现无超调响应,系统输出会存在一定的稳态误差,加强积分环节作用可提高系统位置输出精度,提高快速性,但会产生超调现象。
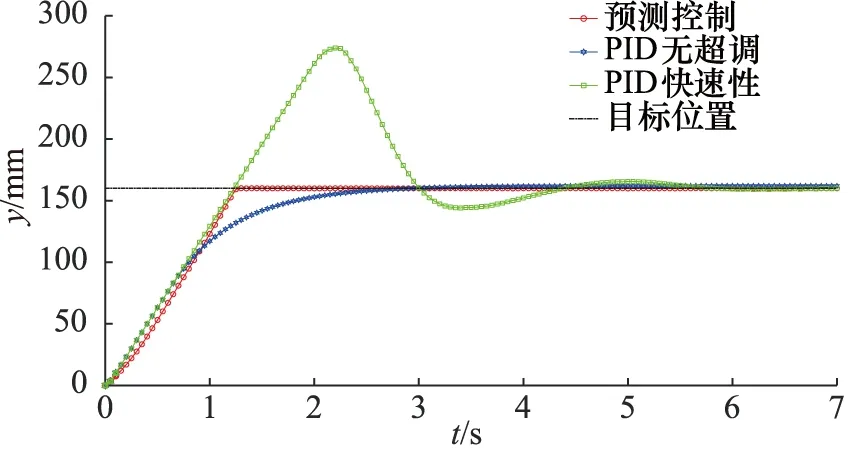
图8 恒负载工况活塞位移输出曲线
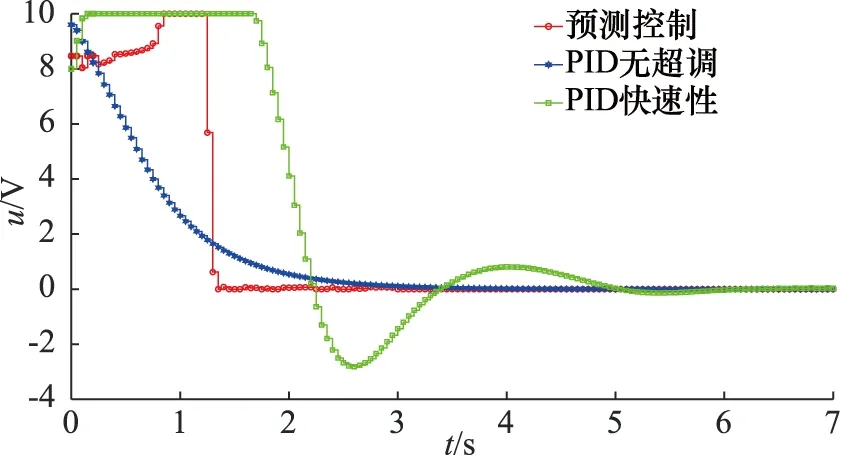
图9 恒负载工况控制器输出电压曲线
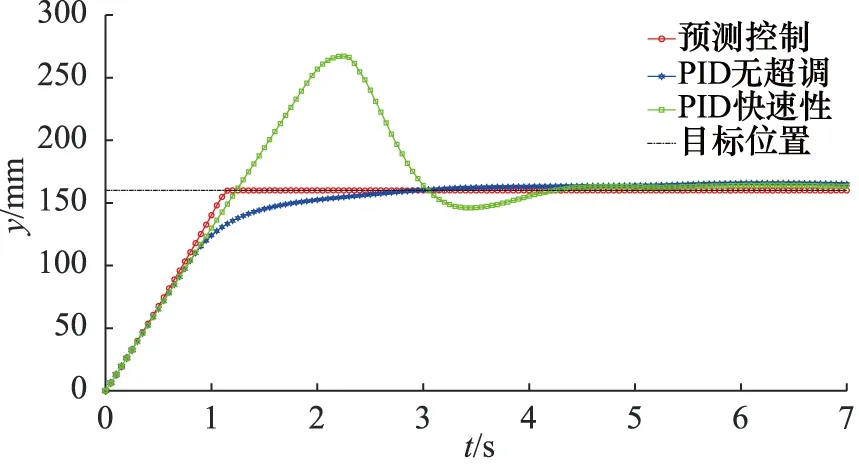
图10 变负载工况活塞位移输出曲线
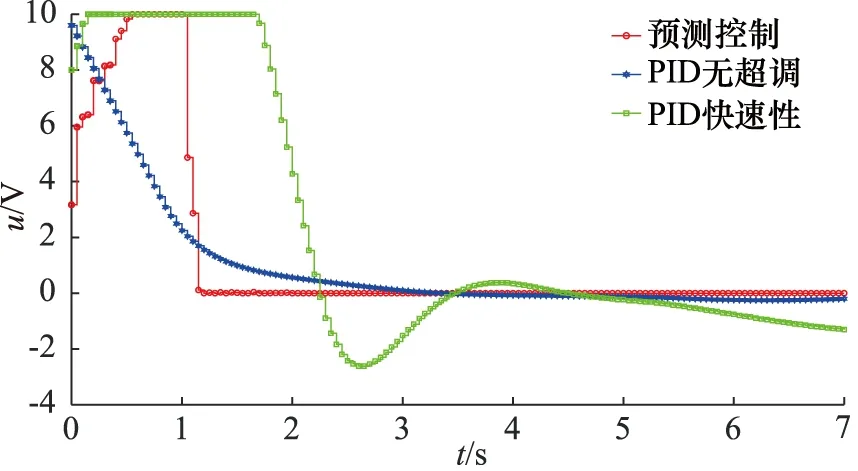
图11 变负载工况控制器输出电压曲线
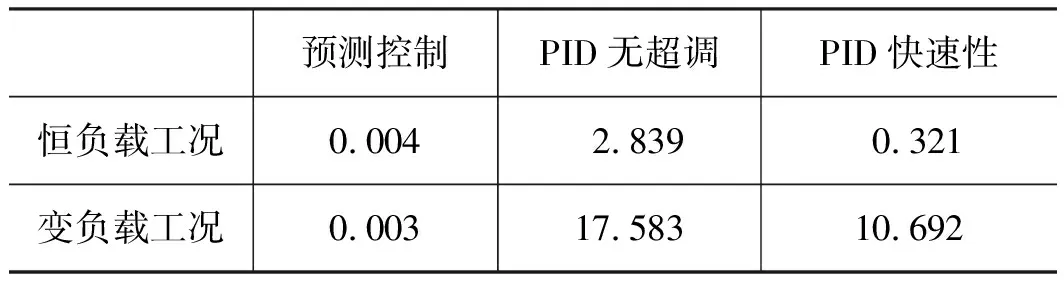
表5 两种工况真实位置均方误差
采用模型预测控制可以实现在控制初期,输出电压信号迅速达到最大值,如图9和图11所示,在即将到达目标位置时,控制值逐渐减小为0 V,调试过程中,位置权重和控制权重的取值变化会影响该过程的动态效果;伺服阀始终单边工作,避免了阀芯切换带来的非线性,位置输出如图8和图10所示,无超调现象发生;从表5可知,稳态时真实位置输出均方误差较小,从图12和图13可知,在恒负载和变负载工况下,稳态误差均小于0.1 mm。因此,采用模型预测控制可以解决阀控非对称缸系统固有特性和采用PID控制导致输出超调和控制效果变差的问题,在不同工况下实现了快速、无超调、精确的位置控制。
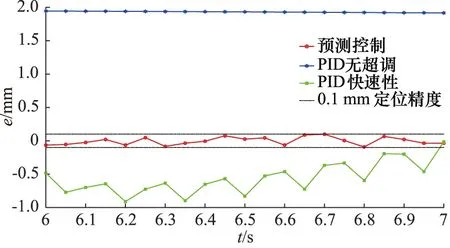
图12 恒负载工况活塞位移稳态误差曲线
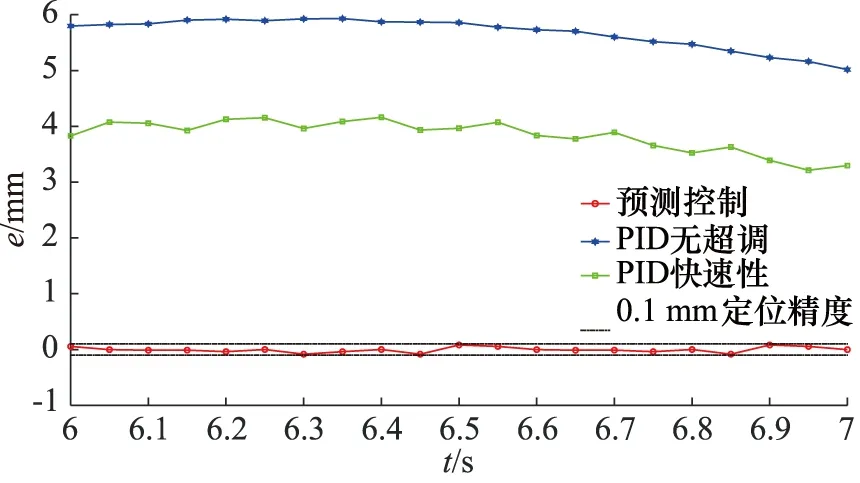
图13 变负载工况活塞位移稳态误差曲线
5 结论
(1) 高斯过程回归实现了对混有噪声数据的拟合处理,自适应获取了超参数,得到了带有置信区间的输出结果。活塞预测位置增量的均方误差较小,建立的离散数学模型精度较高。所需样本数量少,缩短了单步预测时间。
(2) 提出了采用高斯过程回归的阀控非对称液压缸模型预测控制方法,与PID控制相比,解决了为满足快速性或负载发生变化时,输出超调和控制效果变差的问题,实现了快速、无超调位置控制,定位精度满足0.1 mm。
