转弯输送带固有频率及振动特性分析①
2021-08-18赖大港贺福强徐浩然
赖大港 贺福强 徐浩然 李 赟
(贵州大学机械工程学院 贵州贵阳 550025)
带式输送机由于输送能力强、牵引链强度高、结构简单而被广泛应用于食品、药品、流水线生产等传送领域。直线式输送带只能在一直线上输送,在某些特殊情况下不能很好的满足需求。PVC输送带带体弹性好,不易变形,轻巧耐用,具有不易燃性、高强度及优良的几何稳定性. 在自动化产品包装方面,要求的精度相比一般传动更高,因此输送机运行时的平稳性决定了其包装质量,典型的传输共振与跑偏现象直接影响了包装精度,造成错位、遗漏等非规范包装,给产品检测与返工带来不必要的问题,降低了生产效率,增加了成本,且输送带由于振动频率分布问题,严重时会造成一定安全隐患。
许多学者研究了固有频率与振动问题,李德双等[1]分析了轴向运动带的固有频率及振动,得出不同张力下频率值不同;张曼等[2]分析了输送带纵向振动与稳定性,得出不同条件下某阶模态颤振失稳;周广林等[3‐4]分析了横向振动特性,得出适当增大托辊间距,能降低共振频率的影响,同时分析适当调整阻尼比可有效降低横向振动位移;也有研究分析了输送带与托辊的接触情况影响输送带受力、磨损及使用寿命[5‐6]。综上,目前对转弯式输送带振动频率方面研究极少,本研究采用90 度输送带结构,基于有限元分析,建立结构振动微分方程,求解得到固有频率和模态振型,并施加物体输出强迫振动响应,可以为后续的优化设计提供有效的参考,避免出现共振现象,研究转弯输送带振动特性对改善传输生产过程具有重要意义。
1 振动理论模型
1.1 横向振动模型
设x,z 表示沿转弯平面中曲线的纵向和横向,取微元体积为hdxdy,微元中面为x‐y 坐标平面,如图1。
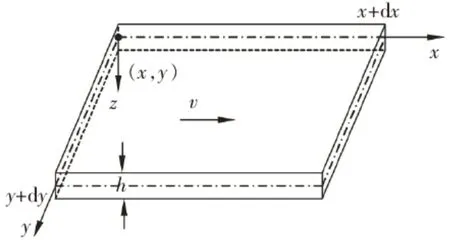
图1 振动微元体


1.2 纵向振动模型

2 转弯输送带有限元模型
分析两端为简支的转弯输送带模型的柔性接触振动,以90°转弯输送带结构进行建模,模型为Kelvin‐Voigt 线性粘弹性体,由线性弹簧和阻尼器并联组成[7],如图 2。若瞬时加上应力σ=σ0=积分得应变当t→ 0 时应变趋于一个稳定值

图2 Kelvin模型
横截面积为A,厚度为h,外圆弧半径为6 m,内圆弧半径为2.5 m,F为输送带初始张力,采用弹性力学平面应力理论,设定参数如表1。

表1 模型参数
3 固有频率和模态振型
模态是机械结构的固有振动特性,结构的每一阶段的模态都具有各自唯一的固有频率、阻尼比以及相应模态振型,结构的模态参数是其本身的固有特性和材料的固有特性所决定的。在求解结构的固有频率和振型时,阻尼对其影响不大,仅与刚度特性和质量分布有关,因此可以忽略[8]。根据达朗贝尔原理,结构振动的一般微分方程可描 述 为
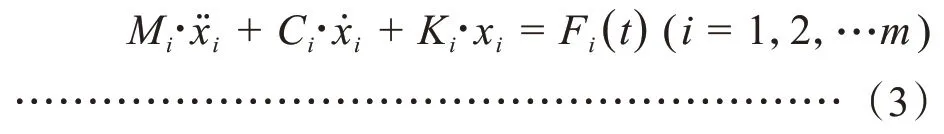
式(3)中,M为振动系统的质量矩阵;C为阻尼矩阵;K为刚度矩阵;F为系统所受的外界激励;x为结构振动的位移向量。
3.1 无约束固有频率
输送带的固有频率先通过分析结构在无载荷无约束的情况下的响应获得,即外界激励F= 0,且C= 0,此时式(3)可简化为

式(6)中:λ为系统的特征值;ψ为特征值对应的特征向量,j为虚数单位;w为系统固有频率,Hz;满足λ=w2即可获得模态分析中的特征值,M、K是产生振动的最基本的原因。

表2 无约束固有频率
由于PVC 材料的自由模态无约束,故1~6 阶为刚体模态,前3 阶固有频率都为0,但第四~六阶不为0,可见低阶模态输送带依然存在振动,故需要考虑共振带来的影响,从第7阶开始有真正频率和振型。
3.2 两端简支约束固有频率
X与Y旋转方向为自由端,不约束,其它方向固定约束。整个系统为欠阻尼,先预估输送带最高频率为10,提取自然频率特征值Eigenvalue 为8阶,模态分析的本质是求矩阵的特征值问题,“阶数”指特征值的个数,求解1~8 阶固有频率和振型如表3。

表3 有约束固有频率
各阶固有频率大小随着阶数的增加而增加,且第1 阶和第2 阶、第3 阶和第4 阶、第5 阶和第6阶、第7 阶和第8 阶的的振型一样,且固有频率大小很接近;对比无约束情况的固有频率与最大变形量可知,边界条件会影响刚度分布,刚度越大,固频越大,振幅越小,刚度越小,固频越小,振幅越大,故需要选取一个频率范围,以保证传输平稳性。
4 振动响应分析
4.1 胶带的动特性
胶带在收到外载荷的作用下,其力学特性不仅仅反应在静态特性的变化,还表现有很复杂的动力特性,应变的大小不仅仅是与应力有关的,还跟上面加载应力的变化以及作用的时间,频率、及环境的温度及材料特性等因素有关,具体表现在[9]:(1) 应力应变的非线性关系;(2) 滞后特性;(3)蠕变特性;(4)松弛特性;(5)频率特性,即输送带的变形量与加载过程载荷的变化频率有关。
为了接近实际结构(图3),获取近似仿真结果,建立转弯输送带与输送物体三维实体离散系统模型(图4),考虑硬接触的穿透性,此处设为软接触,面对面离散,从面网格(输送物体)比主面网格(输送带)细。

图4 有限元模型
4.2 静力下的固有频率与振型
两端加简支约束并设定输送带与输送物体接触,材料属性如表4,对1~8阶固有频率进行计算(图5)可知,1~8阶固有频率依次增加,振型不一样,但最大变形量近似一样。由振型图可知,第1、3、4、7阶频率上输送表面变形最严重,对传输平稳性影响最大,下输送表面基本无变形,此时可适当增加上托辊数与张紧力,调整刚度增大,固频变大,以使振幅减小;下表面第2、5、6、8阶频率输送带上表面基本无变形,传输平稳性较好,但下表面依然变形,其中第6阶下表面穿插到上表面,严重破坏传输结构,此时应设定好下托辊结构,同时选好输入频率,避免发生共振。

图5 静力下1~8阶振型

表4 静力下固有频率与最大变形量
输送带使得重锤式拉紧装置发生上下振动,反过来拉紧装置又是输送带的振动源,它产生的激振力使输送带进行强迫振动[10]。过大的张紧力设计会造成驱动滚筒及机架的设计过大,造成浪费,而张紧力设计过小,则不能使输送带充分张进而不能产生足够的摩擦力进行输送物料,并且容易出现输送带跑偏等问题[11]。在屈服强度和抗拉强度范围内,对输送带两端分别施加500、600、700 N张紧力,分别计算此时的固有频率和振型,结果不一样,可知边界条件一样,预紧力大小依然对固有频率和振型有影响。
4.3 共振频率分析
在静态分析中,结构的最低模态通常控制着结构的响应,振动频率越大,振荡越快,对输送物体的平稳性影响越大。外部激励频率不能跟结构的固有频率接近,否则产生共振,导致变形很大。为了获得低阶固有频率下小的响应振幅,需要对边界条件与激励频率进行合适的设定。已知激励和系统求响应,验算输送带结构工作时的动力响应(如变形、位移、应力等)是否满足预定的要求。但同时考虑输送带和带速受到其他众多条件的限制,不能因为要避免输送机局部的共振就发生改变[12]。此时可重新选择材料。
4.4 振动响应下的疲劳强度
疲劳破坏是多次交变载荷作用下的破坏,抗力与材料组成、构件形状或尺寸、表面接触条件及外部工作环境有关。在输送带耐久性分析上以接触摩擦疲劳为主,即材料的接触表面在接触应力反复作用下出现表面剥落,表现为高应变、高循环次数的应变疲劳。振动响应下输送带的疲劳强度表现为弹塑性断裂中的延性断裂、裂纹的产生、扩展和断裂三个阶段,其中裂纹产生占了整个疲劳的极大部分,因此通过振动分析优化,防止或延迟裂纹产生具有重要意义。
5 结论
(1)此模型材料仅为PVC,作为传送柔性较大,变形较大,故需改变输送带材料刚度,如采用高强度优质尼龙、聚酯帆布作带芯可以改善运输平稳性。
(2)输送带固有频率受张力影响较大,适当增减两端初始张力,可改善振动平稳性,但张紧力不宜过大,否则会导致局部应变疲劳加重。
(3)不同位置点对振动的幅值有较大影响,可适当增减上下托辊数量,改善振动分布。
(4)通过有限元模态分析可看出各阶模态的振动特性、约束条件、输送带的固有频率和振型不同,约束模态激励力下固有频率和振型能反应输送带的振动情况,这为后续优化设计提供参考。
