基于挠曲电效应的悬臂梁式微俘能器动态响应特性研究
2021-08-17于健业李安庆
于健业,李安庆
齐鲁工业大学(山东省科学院) 机械与汽车工程学院,济南 250353
随着便携式电子设备和无线传感器的快速发展,如何为这些低能耗的微电子器件供电成为当前人们关注的热点。微俘能器能直接俘获环境能量转换为电能,实现微电子器件的自供电,从而引起了人们广泛兴趣[1-2]。目前,人们基于压电效应开展了大量的俘能器研究工作,实现了以振动为基础的机械能到电能的转换[3-4]。然而,压电效应仅存在于非中心对称介电材料。同时,具有大压电系数的材料通常是铁电体,使得压电装置表现出迟滞和非线性行为,并且只能工作于居里温度以下[5]。这限制了压电俘能器的应用。
本文综合考虑尺寸效应、阻尼和质量块等因素的影响,建立挠曲电悬臂梁的动力学理论模型,对挠曲电悬臂梁的动态响应特性进行理论研究,分析材料特性、特征尺寸和质量块等因素对俘能器输出功率和能量转换效率的影响规律,为挠曲电俘能器的设计、优化和应用提供理论依据。
1 挠曲电理论
1.1 各向同性挠曲电理论
微尺度下,应变梯度的影响趋于明显。不仅能够解释微构件力学性能的尺寸效应,而且在介电体中能够诱导明显极化,表现出挠曲电效应。挠曲电理论能够描述介电体具有尺寸依赖性的力电耦合现象,其内能密度函数表达为
(1)
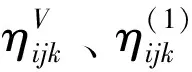
(2)
应变张量和应变梯度张量分别定义为
(3)
其中,ui为位移矢量。应变梯度张量ηijk的3个分量分别定义为
(4)
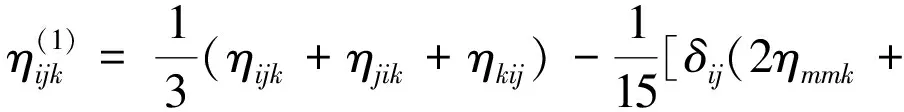
(5)
(6)
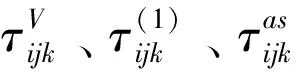
(7)
(8)
(9)
(10)
与应变梯度张量ηijk功共轭的高阶应力张量τijk是3个高阶应力分量的和,表达为
(11)
1.2 挠曲电梁理论
根据伯努利-欧拉梁假设,以梁中性面为x-y坐标平面建立笛卡尔直角坐标系,且x轴沿着梁长度方向,其位移场可表示为
(12)
其中,u、v、w分别是位移矢量在x-、y-、z-方向的分量。假设梁沿着厚度方向发生极化,其它两个方向的极化可以忽略,则其极化场可表示为
P1=P2=0P3=P3(z),
(13)
相应的电位移矢量Di的非零分量为
(14)
式中,ε0为真空中的介电常数,φ为麦克斯韦自电场的势。
把伯努利-欧拉梁的位移方程(12)代入应变、应变梯度的定义式(3),则非零的应变分量和应变梯度分量为
(15)
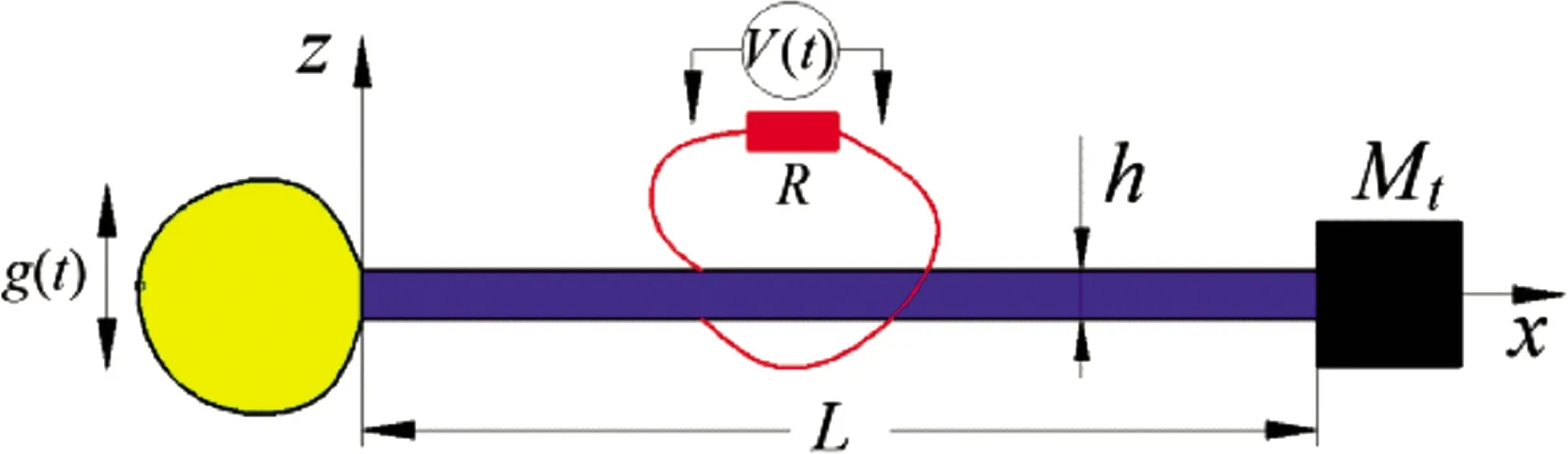
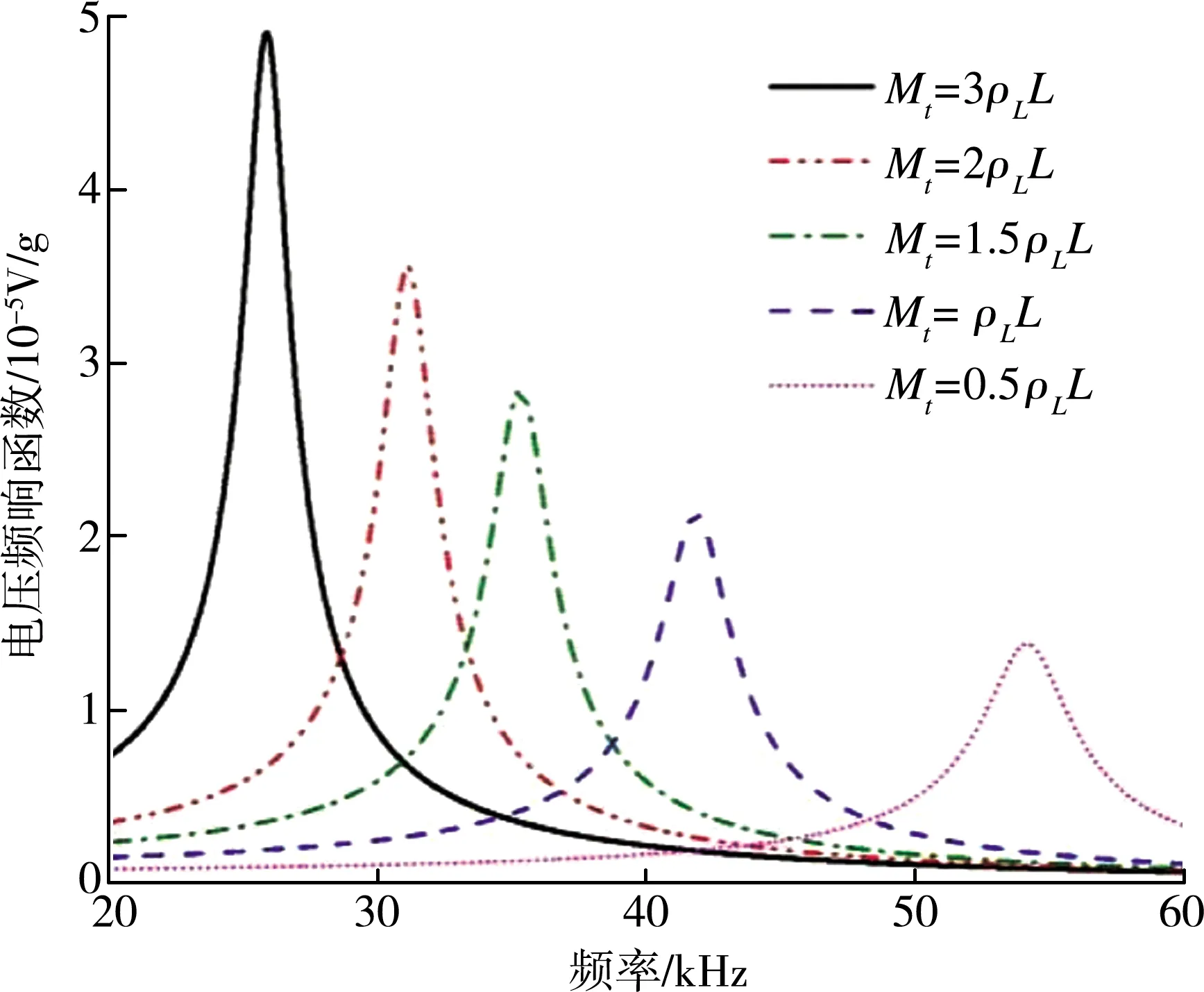
这里需要注意:对于伯努利-欧拉梁h (16) 把非零的应变、应变梯度和极化量代入本构方程式(7)-(10),则功共轭的非零应力、高阶应力和电场量为 (17) 式中,E记作杨氏模量。 挠曲电理论中,由于考虑了高阶应力项,故伯努利-欧拉梁弯曲的应力合力重新定义为 (18) 把非零的应力和高阶应力量式(17)代入式(18),同时考虑式(11),则重新定义的高阶弯矩为零,而弯矩表达为 (19) 极化为 (20) 把(20)代入式(19),同时考虑E3=-V(t)/h(V(t)为梁上下表面的电势差),整理可得 (21) 其中,等效长度尺度参数为 (22) 用应力合力表达的梁弯曲平衡方程 (23) 考虑一悬臂梁式挠曲电俘能器如图1所示,梁宽b,高h,长L,在自由端附加质量块Mt。该挠曲电悬臂梁固定在具有横向振动g(t)的基础上。在基础激励下,挠曲电悬臂梁发生弯曲振动,产生动态应变梯度,从而由挠曲电效应诱导极化,在梁上下表面间产生电势差。悬臂梁的上下表面覆盖电极,连接一个电负载R量化电压输出V(t)。 图1 悬臂梁式挠曲电俘能器简图 在自由端附加质量块Mt的伯努利-欧拉梁,其偏微分控制方程为[6] (24) 其中,wrel(x,t)是挠曲电悬臂梁相对于基础的横向位移;ξs和ξa分别是应变率和空气阻尼系数;I是惯性矩;ρL是挠曲电悬臂梁单位长度质量;wb是位移形式的基础激励[7], wb(x,t)=g(t), (25) 对于伯努利-欧拉梁,高阶弯矩为零,弯矩如式(21)所示。显然式(21)中的最后一项与x坐标无关,当把式(21)代入到式(24)时,最后一项对x的导数为零。为了保证这一项的存在,本文引入了亥维赛函数H(x),弯矩重新表达为 (26) 把式(26)代入到式(24)中,控制方程变为 (27) 其中,δ(x)为狄拉克函数。悬臂梁式挠曲电俘能器的振动响应表达为 (28) 式中,φr(x)是质量归一化本征函数,ηr(t)是第r阶振动模态的模态系数 (29) 其中, (30) 且特征值(λr>0,r=1,2,…)满足方程 (31) 式中,It记作质量块的转动惯量,模态幅值Cr可通过正交条件获得。短路条件下,r阶振动模态的无阻尼固有频率ωr可写为 (32) 把式(28)代入控制方程式(27),同时考虑模态正交条件,力学方程表达为 (33) 其中,模态挠曲电耦合项为 (34) 模态力函数为 (35) 俘能器的电路方程为 (36) (37) 把式(37)代入式(36)中,电路方程进一步写为 (38) 其中,电容C为 (39) 对于悬臂梁式挠曲电俘能器,由式(33)和(38)可得其力学方程和电学方程最终为 (40) (41) 其中,ξ是模态机械阻尼比,满足 (42) 对于简谐基础激励,基础位移的移动分量表达为 g(t)=W0ejωt, (43) 其中,W0是移动位移的振幅;j是单位虚数;ω是频率。把式(43)代入式(35)中,则模态力函数为fr(t)=Frejωt,振幅Fr为 (44) 相应地,假设力学和电学的稳态响应是相同频率ω下的简谐形式 ηr(t)=Hrejωt,V(t)=V0ejωt, (45) 其中,振幅Hr和V0是复数值。力学和电学方程重新表达为 (46) (47) 联立方程(46)和(47),可求解振幅Hr和V0。最终,稳态电压响应表达为 (48) 稳态模态力响应为 (49) 相对于基础的横向位移响应为 (50) 悬臂梁式挠曲电俘能器在基础移动激励下,输出振动和电压响应。由于g(t)=W0ejωt,相应的基础移动加速度是d2g(t)/dt2=-ω2W0ejωt。根据式(44),模态力振幅重写为 Fr=-αrω2W0, (51) 其中, (52) 根据基础的移动加速度,同时考虑式(51),稳态电压响应式(48)表达为 V(t)=κ(ω)(-ω2W0ejωt), (53) 其中,电压输出频响函数为 (54) 同理,稳态振动响应式(50)表达为 wrel=χ(ω,x)(-ω2W0ejωt)+m(ω,x)(-ω2θ0ejωt), (55) 其中,横向位移输出频响函数为 (56) 悬臂梁式挠曲电俘能器工作在共振频率ω≅ωr时将获得最大的输出响应。在该条件下,仅考虑r阶振动模态即可。因此,根据式(48)和(50),稳态的电压和横向位移响应可简化为 (57) (58) 同时,在式(53)至(56)的频响函数中仅保留r阶模态的贡献。则稳态的单模态电压响应为 (59) 其中, (60) 稳态的单模态位移响应为 (61) 其中, (62) 本节仿真研究悬臂梁式挠曲电俘能器在基础简谐式移动激励下的动态响应。梁材料为聚偏二氟乙烯。材料特性为E=3.7 Gpa;ρ=1.78×103kg/m3;ε0=8.854×10-12C2/(N·m2);a=1.38×1010N·m2/C2;l=1 μm;f=-179 N·m/C 。 梁的几何参数为h=0.3 μm;b=3 μm;L=30 μm。质量块质量为Mt=1.5ρbhL。 悬臂梁式挠曲电俘能器的电压输出频响函数如图2所示。从图2可以看出,不同振源频率下,挠曲电俘能器的输出电压不同。当振源频率等于俘能器的自振频率时,俘能器输出最大的电压响应。此外,随着尖端质量的增大,俘能器共振频率减小,相应的电压输出单调增大。尖端质量能够调整悬臂梁的固有频率,使之适应环境振源频率。 图2 不同尖端质量下电压频响函数随频率的变化 悬臂梁式挠曲电俘能器的横向位移频响函数如图3所示。负载电阻对俘能器的变形挠度也有较大影响。随着电路从短路到开路(电阻从零增大到无穷大),悬臂梁式挠曲电俘能器的固有频率从34 701 Hz偏移到35 411 Hz。在某些电阻下,由于电阻的并联阻尼,尖端挠度减弱。该现象与压电俘能器相类似。 图3 不同负载下尖端挠度频响函数随频率的变化 此外,可以通过|V(t)|2/R计算挠曲电俘能器的电功率,且功率密度频响函数如图4所示。从图中可以看出随着电阻的增大,功率密度先增大后减小,表现出相反的趋势。这说明一定存在一个电阻值使得功率密度达到最大值。对于当前情况,当电阻在100 MΩ左右时,功率密度达到最大值,此时相应的共振频率为34 830 Hz。 图4 不同电负载下电压频响函数随频率的变化规律 本文基于挠曲电理论,研究了自由端附加质量块的挠曲电悬臂梁在基础激励下的力电耦合特性。首先,建立了悬臂梁式挠曲电俘能器的理论模型。然后,解析了俘能器在简谐激励下的稳态力电耦合响应。最后,仿真了基础移动激励下悬臂梁式挠曲电俘能器的俘能特性。研究发现,随着电负载增大,电压输出增大,电流输出减小,而电功率先增大后减小。当电阻在100 MΩ左右时,电功率输出达到最大值。随着电负载从零到无穷大(从短路过渡到开路),共振频率从34 701 Hz偏移到35 411 Hz,尖端质量能够调整悬臂梁固有频率,使之与振源频率相一致。从而使俘能器工作在共振频率下,显著提高能量俘获效率。
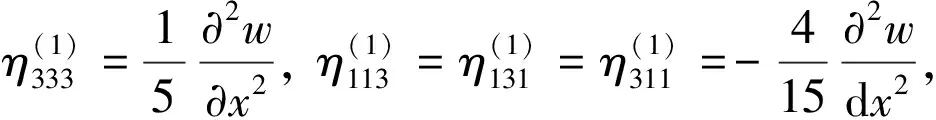

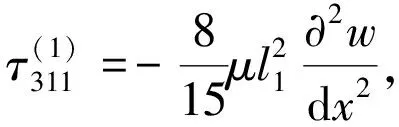

2 悬臂梁式挠曲电俘能器理论建模
2.1 力学方程



2.2 电学方程
2.3 稳态响应
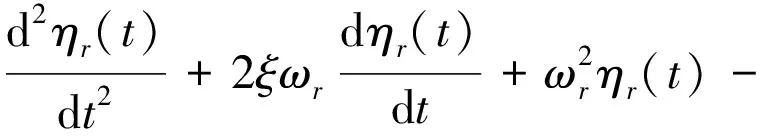
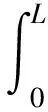

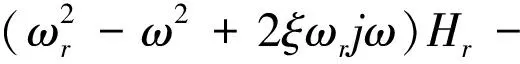

3 俘能特性研究
4 俘能器动态响应特性


5 结 论
