基于神经网络的非线性随机系统有限时间环域稳定性与镇定
2021-08-17严志国苏方旭
严志国,苏方旭,陈 耀,张 敏
1.齐鲁工业大学(山东省科学院) 电气工程与自动化学院,济南 250353 2.齐鲁工业大学(山东省科学院) 数学与统计学院,济南 250353
非线性随机系统作为一类重要的随机系统,已被广泛应用于电力系统、通讯系统等实际工程领域[1],并在这些领域中发挥了非常重要的作用。因此,非线性随机系统的研究受到越来越多的关注。例如,FLORCHINGE等[2]给出了Artstein定理的一种扩展,并得到了非线性随机系统的一种反馈控制方法。LIU等[3]研究了非线性随机系统输入状态稳定性,并给出了判定条件。WU等[4]研究了状态依赖切换随机系统的稳定性问题。YAN等[5]利用神经网络技术研究了非线性随机系统的有限时间镇定问题,YAN等[6]进一步研究了非线性随机系统的有限时间H∞控制问题。
另一方面,与传统意义的渐近稳定性相比,有限时间稳定性能更好地描述系统在给定时间区间内的暂态行为。因此,对于某些工作时间较短的系统或系统状态必须满足给定限制范围的情况,可以在有限时间稳定的基础上进行系统分析与控制[7]。然而,在某些情况下,有限时间稳定性还不能满足系统所需要的暂态性能的要求。这是因为有限时间稳定性仅仅对系统状态的上界限进行约束,对其下界限并没有要求。但是对于工程中的某些实际系统,对系统状态的下界限也有着严格的要求[8]。此外,在电子电路系统中,需要控制二极管的电压在0.3~1.0 V之间,以使整个电子电路系统可以在给定时间内工作[9]。为此,YAN等[10-11]引入了有限时间环域稳定性的概念来改进这一问题。此外,在该领域,还有许多学者也取得了丰富的研究成果[12-13]。但对于不确定性非线性随机系统的有限时间环域稳定性与镇定问题,尚未有相关研究。本文利用神经网络逼近系统中的非线性项,研究了不确定性非线性随机系统的有限时间环域稳定性与镇定问题。
1 预备知识
1.1 系统描述
考虑如下不确定非线性随机系统:
(1)
[ΔA1ΔA2]=MF(t)[N1N2],
其中,M、N1、N2是已知适当维数的矩阵,且F(t):R→Rk×l是未知的时变函数,满足:
F′(t)F(t)≤I,∀t>0.
下面引入不确定非线性随机系统有限时间环域稳定性的概念。
定义1:文献[10]给定正参数T、ci其中i=1、…、4,且c4>c2>c1>c3>0和矩阵R>0。如果对∀t∈[0,T],满足:
c1≤E[x′(0)Rx(0)]≤c2⟹c3≤E[x′(t)Rx(t)]≤c4,
(2)
则称非线性随机系统(u(t)=0)是关于(c1,c2,c3,c4,T,R)有限时间环域稳定的。下面介绍有限时间环域镇定,构造如下状态反馈控制器:
u(t)=K(t)x(t),
其中,K(t)=K+ΔK(t),ΔK(t)是一个扰动矩阵,且假设:
ΔK(t)=D3F(t)N3,
其中D3,E3是已知适当维数的实常数矩阵。
定义2:如果存在状态反馈控制器u(t)=K(t)x(t),使得如下闭环系统是有限时间环域稳定的,
(3)
则非线性随机系统对所有允许的不确定性都是有限时间环域可镇定的。
本文的目的是设计一个状态反馈控制器,使闭环系统对所有允许的不确定参数是有限时间环域稳定。
使用LIMANOND等[14]提到的线性微分包含(Linear difference inclusion,LDI)技术,用多层神经网(Multi-layer neural networks,MNNs) 逼近非线性函数f(x(t))[15]。
上述神经网络简略结构如图1所示(以3个输入向量的单隐藏层神经网络为例):
在不失一般性的前提下,设单隐藏层感知器N(x(t),W1,W2)被适当训练以近似非线性项f(x(t)),可用矩阵向量表示为:
N(x(t),W1(x(t)),W2(x(t)))=
ψ2[W2ψ1[W1x(t)]],
(4)
其中,Wi∈Rn×n、i=1,2,为神经元的连接权矩阵,ψi(·)为神经网络的激活函数向量,其定义为:
ψi[ζ]=[φ1(ζ1),φ2(ζ2),…,φni(ζni)]′.
令:
j=1,2,…,ni
则激活函数φj的最大、最小导数定义如下:
且激活函数φj可以用如下形式重写:
φj=hj(0)sj(0,φj)+hj(1)sj(1,φj),
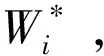
(5)
其中,D∈Rm是一个紧集,使得
表示第i层的ni维索引向量(i=1,2)的集合为:
κni=κni(σ)={σ∈Rni|σj∈{0,1},j=1,…,ni},
其中σ被用作二进制指示符。显然,有ni个神经元的第i层具有2ni个二进制组合指示器(k=0,1)。两层NNs的索引向量元素有2n2×2n1组合Θ=κn2⊕κn1。
利用LIMANOND等[14]的表示方法,上式可以表示为:
=Σσ∈ΘμσAσ(σ,ψ,W*)x(t),
其中,
h1n1(k1n1)…h11(k11)=1,
hij(σij)≥0,σij=0,1
hij(0)+hij(1)=1,i=1,2,j=n1,n2.
因此,闭环系统(3)可以转化为一组误差有界的线性微分包含,即:
(6)
其中,
并且
表示神经网络的逼近误差。
1.2 引理
为推导出本文主要的结果,首先介绍如下几个引理。
引理 1:(Gronwall 不等式)
令θ(t)是一个非负函数,若对任意的a>0,b>0满足:

则有如下不等式成立:
θ(t)≤aebt,0≤t≤T.
引理 2:(反向Gronwall 不等式[11])
令θ(t)是一个非负函数,若对任意的a>0,b>0满足:

则有如下不等式成立:
θ(t)≥aebt,0≤t≤T.
引理 3:令A、B、S和F是适当维数的实数矩阵,且满足F′(t)F(t)≤I,则对任意的正数ε>0,有如下不等式成立:
S+AF(t)B+B′F′(t)A′≤S+εAA′+ε-1B′B.
引理 4:(Shur’s 补引理)对任意的实数矩阵N、实对称矩阵A、D,如下两个不等式是等价的:
1)A-BD-1B′<0,
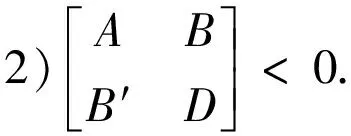
2 有限时间环域稳定性与镇定
本部分考虑不确定非线性随机系统(3)有限时间环域镇定问题。首先,给出系统为有限时间环域稳定的一个充分条件。
定理1:如果存在α>0,β>0,正定矩阵Q以及矩阵K,使得下列不等式成立:
(7)
(8)
(9)
(10)
则系统(3)关于(c1,c2,c3,c4,T,R)是有限时间环域稳定的。
其中,
证明:下面将分为两步证明此结论。
第一步:
c1≤E[x′(0)Rx(0)]⟹c3≤E[x′(t)Rx(t)]
(11)
然后,考虑如下不等式:
(12)
其中,
在(7)式前后同时乘
可以得到:
(13)
根据引理3,不等式(13)等价于
(14)
并且蕴含着:
(15)
通过比较(12)和(15)式可以得到如下结论:
(16)
对(16)式两边同时从0到t取积分,t∈[0,T], 并且取数学期望可得:

(17)
根据引理1,上述不等式可以写成:
EV(x(t))>V(x(0))eαt。
(18)
根据条件,可以得到:
EV(x(t))=Ex′(t)R1/2Q-1R1/2x(t)
≤λmax(Q-1)Ex′(t)Rx(t),
(19)
并且
V(x(0))eαt=x′(0)R1/2Q-1R1/2x(0)eαt
≥λmin(Q-1)x′(0)Rx(0)eαt
≥λmin(Q-1)c1。
(20)
根据(19)和(20),可以得到:
(21)
然后根据条件(7),可以得到:
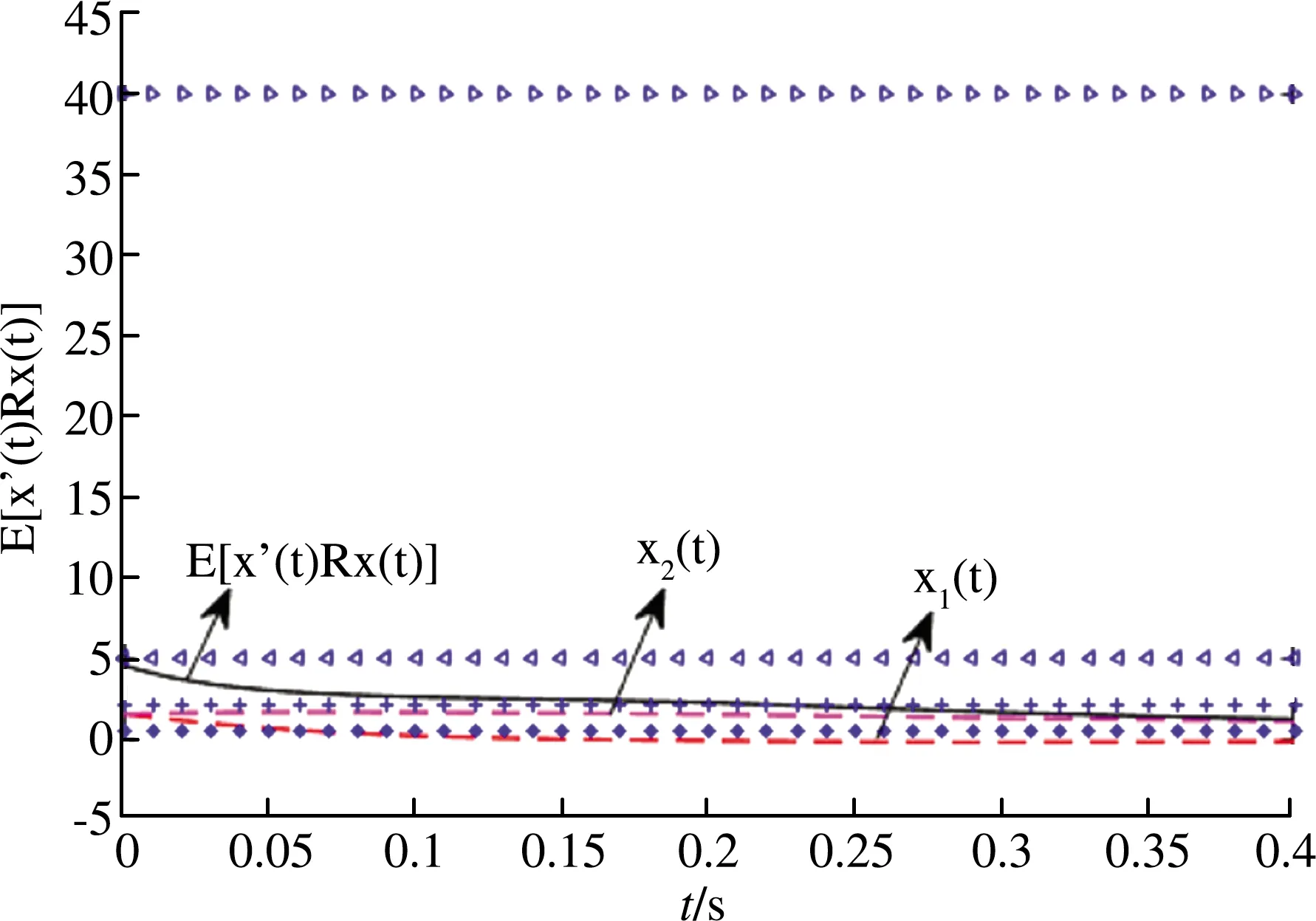
c3 (22) 第二步: E[x′(0)Rx(0)]≤c2⟹E[x′(t)Rx(t)]≤c4, (23) 可以得到: (24) 根据引理3,上述不等式等价于: (25) 通过比较(25)和(23)式可以得到如下结论: (26) 对上述不等式两边同时从0到t取积分,t∈[0,T],并且取数学期望可得: (27) 根据引理1,上述不等式可以写成: EV(x(t)) (28) 根据此定理的条件,可以得到: EV(x(t))=Ex′(t)R1/2Q-1R1/2x(t)≥ λmin(Q-1)x′(t)Rx(t), (29) 并且 V(x(0))eαt=x′(0)R1/2Q-1R1/2x(0)eβt ≤λmax(Q-1)x′(0)Rx(0)eβt ≤λmax(Q-1)c2eβt。 (30) 根据(29)和(30),可以得到: (31) 然后根据条件(10),可以得到: Ex′(t)Rx(t) (32) 证毕。 定理1中的条件是由非线性矩阵不等式所描述,难以求解。因此,下面的定理给出了由线性矩阵不等式所表示的充分条件。 (33) (34) λ1I (35) c3λ2-c1λ1<0, (36) c2λ2eβT-c4λ1<0, (37) 其中, ε1MM′+ε2B1D3D3B1′, 证明:分两步证明。 第一步: 替换(7)中 则(7)可以写成: (38) 其中, 可以采用如下方法来分析系统中的不确定性: Z=Π+ΔΠ, 其中, 由引理2可得: ≤M1+M2+M3+M4+M5+M6+M7+M8 (42) 其中, 根据引理3,等价于: Z≤ 其中, (43) 因此,令不等式(43)的右边小于0,即: <0, (44) 第二步: 替换(8)中 则(8)可以写成: (45) 其中, 可以采用如下方法来分析系统中的不确定性: Z=Υ+ΔΥ, (46) 其中, (47) (48) 由引理2可得: ≤M1+M2+M3+M4+M5+M6+M7+M8 (49) 其中, 根据引理3,(46)等价于: (50) 其中, 因此,令不等式(50)的右边小于0,即: (51) 本部分利用定理1、定理2的结论考虑如下特殊形式的非线性随机系统有限时间环域镇定问题: (52) 下面给出使得上述系统有限时间环域镇定的状态反馈控制器存在的充分条件。 (53) (54) (55) c3λ2-c1λ1<0, (56) c2λ2eβT-c4λ1<0, (57) 其中, 则称上述系统是有限时间环域镇定的。 算法1: 第一步:给定c1,c2,c3,c4,R以及T。 第二步:以h1为步长取一列αi(i=1,…,n),并且以h2为步长取一列βj(j=1,…,n)。 第三步:令i=1,取αi。 第四步:令j=1,取βj。 第五步:如果找到(αi,βj)使得(53)-(57)有可行解,则把(αi,βj)存入(X(i),Y(j))。令βj=βj+1并且转到第五步。否则,转到第六步。 第六步:如果i+1 第七步:如果(X(i),Y(j))=(0,0),则找到的(α,β)使得(53)-(57)无可行解。否则,存在(α,β)使得(53)-(57)有可行解,停止。 算例1:考虑非线性随机系统(52)如下: 估计近似误差的上界为ρ=0.003。显然,在这种情况下,有Θ=23×21。并且Aσ可以得到如下表达式: 应用算法1,得到α和β的取值范围,如图2所示。 图2 α和β的取值范围 控制输入u(t)的变化过程如图3所示。 图3 u(t)的变换过程 另外,给定α=0.5、β=1,求解得到的矩阵不等式得到: λ1=4.369 5,λ2=12.670 7。 图4表明了系统E[x′(t)Rx(t)]的变化过程。其中四条蓝线分别表示c1-c4四个给定的界限,当系统初始值满足条件c1 图4 系统状态的变化过程 综上所述,闭环系统关于(2,5,0.5,40,I)是有限时间环域稳定的。 本文给出了一类不确定非线性随机系统的有限时间环域稳定性的定义。在线性微分包含状态空间表示的基础上,将神经网络控制系统的一般设计方法推广到不确定非线性随机系统。利用线性矩阵不等式技术解决了状态反馈控制器的设计问题。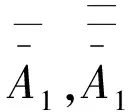

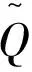





3 非线性随机系统有限时间环域镇定
4 算法及仿真



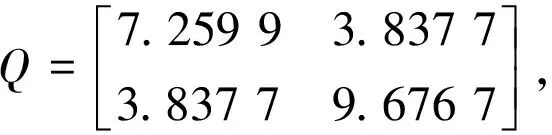
5 结 论
