基于有限元模型的气液两相弹状流混输管线振动特性研究

刘 刚,赵志范,高 源,娄珊珊,于志颖,郝宗睿

齐鲁工业大学(山东省科学院) 海洋仪器仪表研究所,青岛 266061

气液两相混输管线广泛应用于深海油气资源的开采过程中。大量研究表明,当流体流经管道时会引起管道的振动,并且会使得管道系统的固有频率发生一定程度的变化。当管道内的流速达到临界值时会使得管道系统发生各种失稳从而引发管道的损坏[1]。

在输流管道的动力学研究方面,学者们开展了输流管道固有频率方面的研究[2-5],他们普遍得出结论,对于输送单相流体而言,随着流速的增大管道系统的固有频率会随之减小,而不同管道支撑下系统固有频率特性可以参见文献[6]。关于输流管道系统的振动,学者们利用伽辽金模型能够获取几种简单的边界支撑下(如两端简支、悬臂管道系统等)系统的振动强度及频率等特性,而针对复杂的边界支撑,使用伽辽金模型较难获取振型函数,此时需要借助有限元方法获取管道系统的固有频率等振动特性。

相比于单相输流管道,气液两相管道系统的振动特性跟两相流的流动特性有着密切的关系[7-10],在众多的两相流流型中,弹状流是较为复杂的一种,由于弹状流的间歇性特征,使得通过管道中的某一点的流体流速密度等参数不断发生变化,进而可以推断输送气液两相弹状流的管道系统的动力学特性会更为复杂[11]。

本文将基于有限元方法构建弹状流管道系统振动模型,对不同工况下管道系统固有振动特性进行分析。

1 管道振动模型构建

本文研究输送气液两相弹状流管道系统的动力学特性,忽略管道外部运动阻尼。采用有限单元法,根据文献[6],单相流体的管道振动模型为:

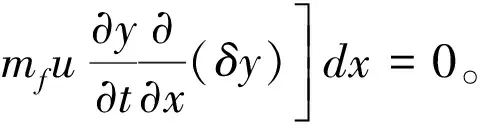
(1)

其中,EI为管材抗弯刚度；mp和mf分别为管道和流体的线密度；u表示流速；y表示在垂直于流体流动方向上管道振动的位移；AiP表示管道面积同流动压力的乘积；l表示有限单元长度。

上述公式适用于输送单相流体的管道系统,但是对于输送气液两相弹状流体的管道系统,由于两相流的各相流体的流动速度以及密度等性质不再相同,上述方程中的参数,如流速以及单位长度流体的质量等需重新定义,如下所示:

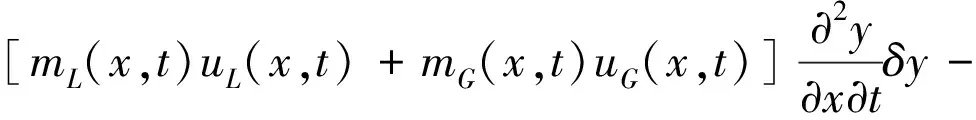
(2)

采用有限单元法,令:

δy=[N(x)]δ[φ(t)]。

(3)

其中N(x)和ϕ(t)分别表示形函数矩阵和节点位移向量。

将式(3)代入到(2)中,得:

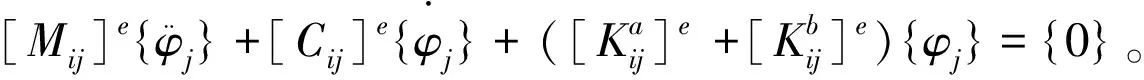
(4)

其中,

(5)

mG(x,t)uG(x,t)][N′]T[N]dx,

(6)

(7)

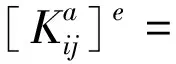
(8)

对于气液两相弹状流而言,由于其间歇性特征,通过管道上某一点的流体流速会随着流动的进行而发生变化,而在某一瞬时,通过管道上各个点的流体的流速等也不尽相同,因而上述变量均为时间与位置的函数。而解决上述问题的难点在于如何求解某一时刻通过管道上某一点的气液流速以及单位长度流体的质量等参数。

图1为弹状流动过程中的某两个瞬间的示意图,在坐标x处液体的流速在t1时刻为通过坐标x的液膜区的流动速度,但是在t2时刻却等于通过x的液弹区的流动速度,因而通过一定的运算才能得到在某一时刻通过管道上面各个点的气液两相的流动速度以及其他参数,并最终得到总体矩阵方程如式(9)所示。

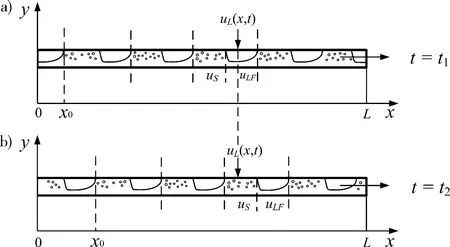
图1 弹状流两个不同时刻示意图

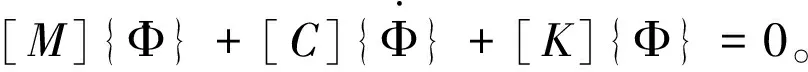
(9)

其中,[M]、[C]和[K]分别是总体质量、阻尼和刚度矩阵。参照文献[11]和[12]可得管道系统的固有频率。

2 模型讨论分析

在下面的分析中,假定管内流动的两相工质为空气和水,密度分别为1.20 kg/m3和998 kg/m3,以左端固定右端简支的管道系统为研究对象参数设定为:弹性模量E=210 GPa,管道内、外径分别为内径Di=0.030 m、外径D=0.040 m,管长设置为20 m。因为本文主要考虑气液两相弹状流型,根据文献[13],选取水的折算流速为1.0～1.4 m/s的范围,每种液相工况下空气的折算流速在1.0～10.0 m/s范围内变化时,气液两相所产生的流型为弹状流。而气液两相的折算流速所反映的分别是气液两相流量的变化。

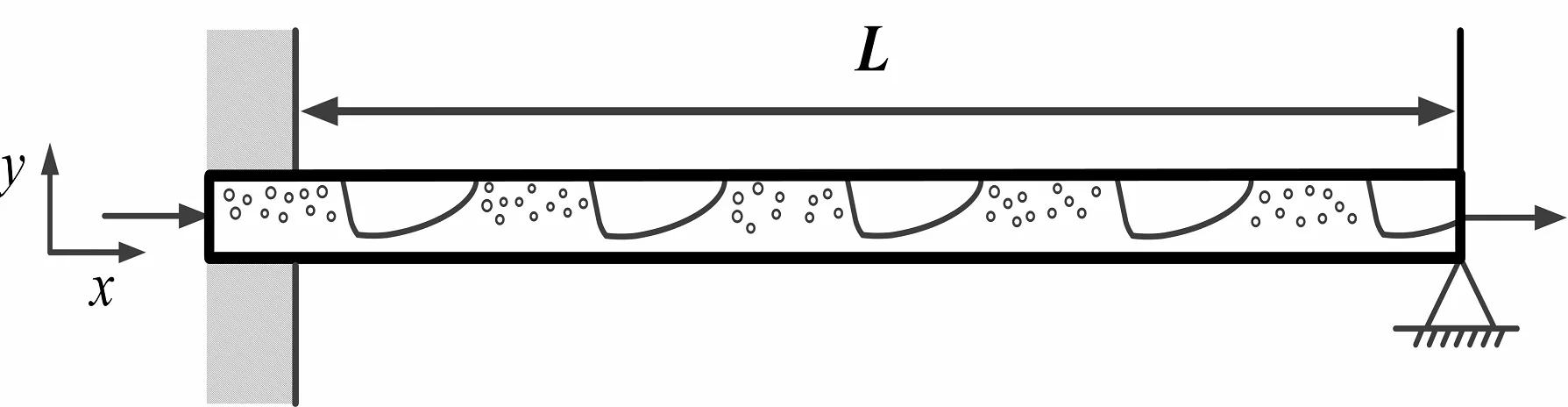
图2 一端固定一端简支的管道系统示意图

图3为折算液速保持为1.0 m/s时,管道系统固有频率在不同气相流量下的时域规律,从图中可以看出,在任何折算气速下,管道系统的固有频率都在发生一定的变化,而且近似地可以看出可能是发生周期性的变化,为了能够更加直观地观察固有频率的变化规律,我们以其中的某一个折算气速4.0 m/s为例分析固有频率随时间的变化规律。

图4为折算气速为4.0 m/s而折算液速为1.0 m/s时管道固有频率随时间的变化与通过管道中点的液相流速的比较。

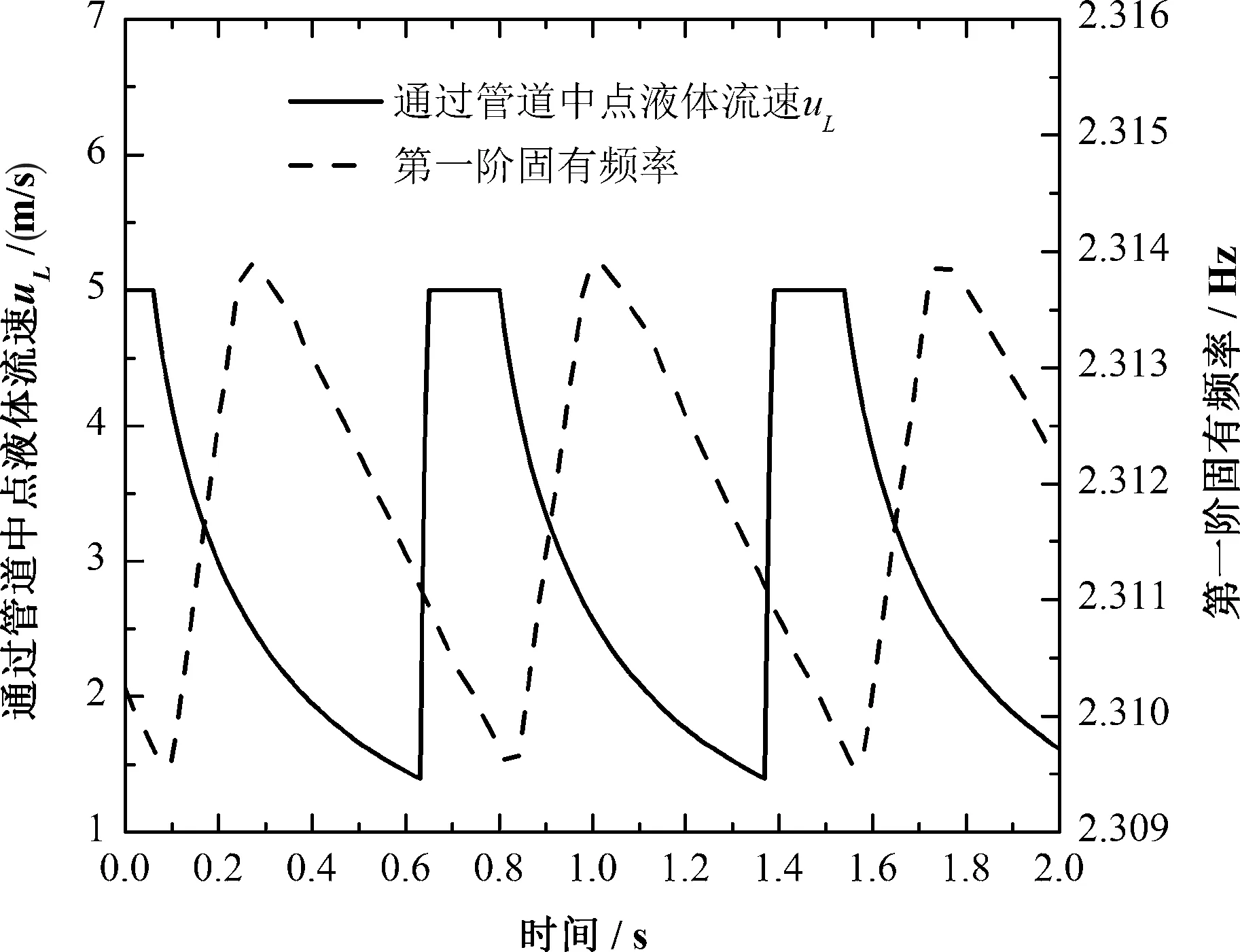
图4 管道固有频率随时间的变化与通过管道中点的液相流速的比较

从图中可以看出随着流动的进行,管道的固有频率在发生周期性变化,而变化的周期和弹状流的运动周期是一致的。对于输送两相弹状流的管道系统而言,由于气液两相流体在速度以及密度方面都存在一定的差异,因而管道系统的固有频率随气液两相的折算速度的变化会较为复杂。

图5为折算气速保持2.0 m/s,不同折算液速下系统的固有频率随时间变化的趋势,固定气相流量,增大液相流量,则固有频率减小。

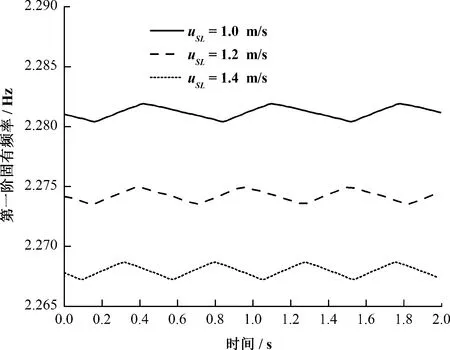
图5 折算气速保持2.0 m/s,不同折算液速下系统的固有频率随时间变化的趋势

图6为折算液速为1.4 m/s时,管道系统的固有频率随气相流量的变化规律,可以看出,管道的固有频率在任意时刻的固有频率都会随着气相流量的增大而增大,这主要是由于随着折算气速的增大,虽然气体的速度增加了,但是由于气体的密度较小而液体的密度较大,固定气液比,增大气相流量,固有频率会增大。

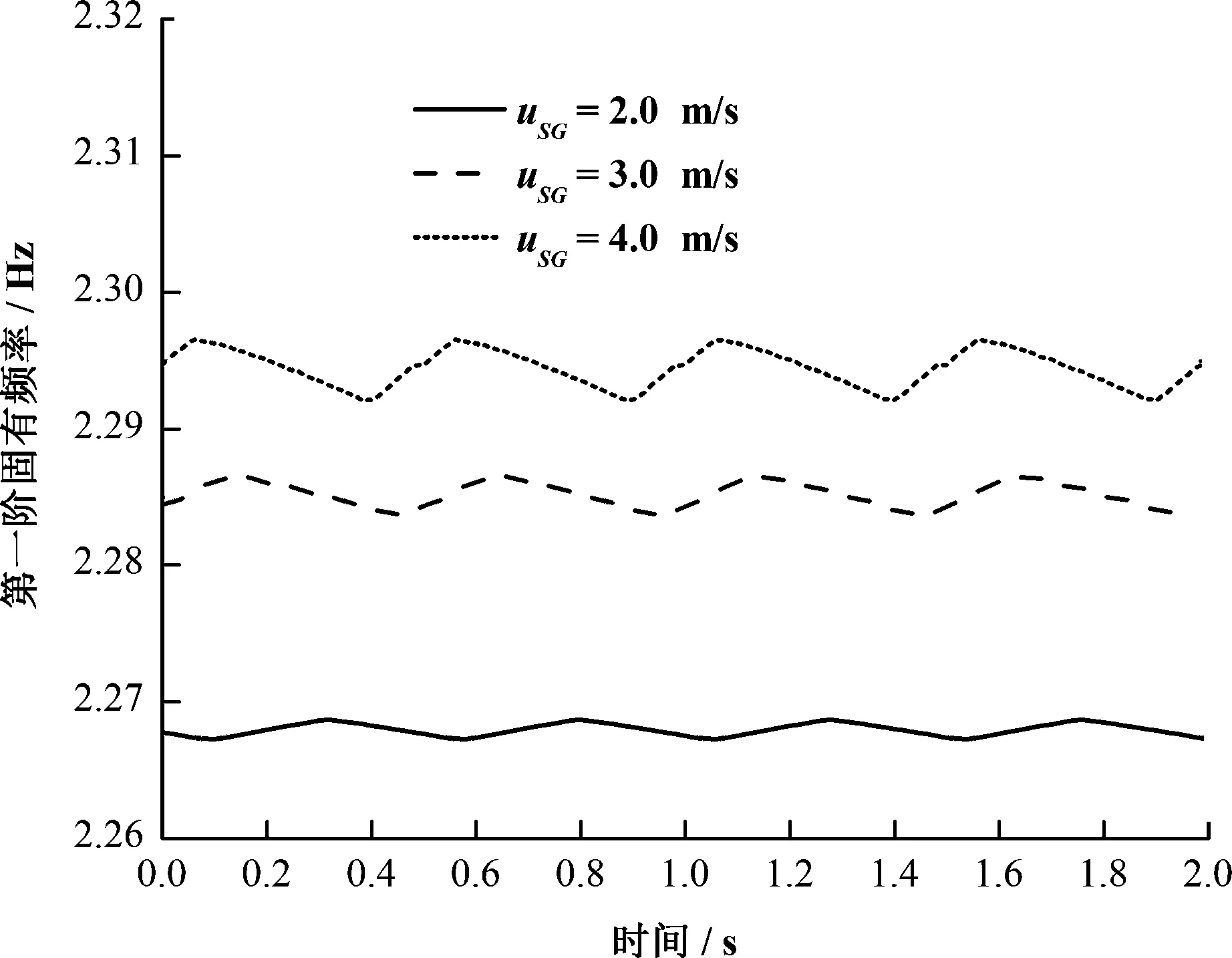
图6 折算液速保持1.4 m/s,不同折算气速下系统的固有频率随时间变化的趋势

但是当折算气速进一步增大时,如图7所示。

当折算气速为10.0 m/s时,管道系统的固有频率虽然在某些时刻会大于折算气速为4.0 m/s时的固有频率,但可以看得出来在绝大多数时刻其固有频率的值是小于折算气速为4.0 m/s时的值的,这说明,在某些时刻大的气相流量下的固有频率仍旧大于小的气相流量下的固有频率,但总体趋势是,大的折算气速下的固有频率会在绝大多数时刻下小于小的折算气速下的固有频率。至于出现这种现象的原因主要是由于气液两相的流速以及两相的比例不同所决定的。虽然气体密度小于液体密度,但是由于流速过大,会出现随着折算气速的增大固有频率降低的情况。

3 结 论

本文参照输送单相流体的管道系统,建立了输送气液两相弹状流的管道系统动力学方程,使用有限单元法对所建立的方程进行了求解,重点考虑了弹状流的间歇性特征。分析了不同气液两相流量下管道系统固有振动特性。研究结果表明:

1)对于输送气液两相弹状流的管道系统,其固有频率随着流动的进行做周期性的变化,变化周期同弹状流的周期相同。

2)对于不同的两相工况,固定气相流量,管道系统的固有频率时域值随着液相流量的增大出现明显减小的趋势；当固定液相流量时,管道系统固有频率的变化规律随着液相流量的增大会呈现出多样性,会出现固有频率随着液相流量增大而增大的现象,但是随着气相流量的进一步增大,气相流量较大下的固有频率会在绝大多数时刻下小于气相流量较小时的固有频率。