Be dding plane-emb e dde d augmente d virtual internal bonds for fracture propagation simulation in shale

Zihn Liu ,Zhennn Zhng ,∗ ,Ahmd Ghssemi

a Department of Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

b Mewbourne School of Petroleum and Geological Engineering, The University of Oklahoma, Norman, OK 73091, USA

Keywords:Shale Bedding plane Constitutive model Hydraulic fracture Augmented virtual internal bond

ABSTRACT To effectively simulate the fracture propagation in shale,the bedding plane (BP) effect is incorporated into the augmented virtual internal bond (AVIB) constitutive relation through BP tensor.Comparing the BP-embedded AVIB with the theory of transverse isotropy,it is found the approach can represent the anisotropic properties induced by parallel BPs.Through the simulation example,it is found that this method can simulate the stiffness anisotropy of shale and can represent the effect of BPs on hydraulic fracture propagation direction.Compared with the BP-embedded virtual internal bond (VIB),this method can account for the various Poisson’s ratio.It provides a feasible approach to simulate the fracture propagation in shale.

The rock with parallel bedding planes (BP) is quite popular in practical engineering.These BPs make the rock transverse isotropic and significantly affect the fracture propagation in such rock.So far there are generally two approaches to consider the BP,namely the discrete and the continuum approach.In the discrete approach,the BP is individually considered in the numerical model.For instance,Zhao et al.[1] modeled BP by contact interfaces.Li and Zhang[2] considered the BP effect in cohesive finite element method by assigning the interfaces parallel to BP with different parameters.In the discrete approach,the BP can be individuality accounted through a straightforward manner.However,it is hard to handle the massive BPs by the discrete approach since it usually involves a lot of degrees of freedom.

In the continuum approach,the BP is accounted through the constitutive relation.For instance,Li et al.[3] coupled a cylindrical microplane system with the classical spherical microplane one[4] together to reflect the transverse isotropy induced by BPs.This method is efficient to represent the high degree of anisotropy of shale.Nguyen and Le [5] developed a microstructure tensor-based method to formulate the anisotropic rock.Compared with the discrete approach,the continuum one has great advantage in reducing degree of freedom.Thus,it is easy to handle the massive BPs.But the continuum method has some limitations in fracture simulation in that it needs a separate fracture criterion to predict fracture propagation.It is hard to find a suitable fracture criterion for the anisotropic rock.

Recently,Zhang et al.[6] proposed a new approach to model the shale with consideration of BPs in the virtual internal bond(VIB) model [7] .In this method,a BP tensor is defined to quantify the BP distribution.To account for the BP effect,the bond distribution density is associated with the BP tensor.However,in this work,the Poisson’s ratio is fixed.In this letter,we incorporate the BP tensor into the augmented virtual internal bond (AVIB)model [8] in order to improve model accuracy of VIB.The BPembedded AVIB can handle the massive BPs through constitutive relation and can avoid the separate fracture criterion in fracture simulation.

The AVIB [8] is a micro-macro constitutive model that stems from the VIB [7] .The representative element volume (REV) of VIB consists of bond network on the micro scale (Fig.1 a).In AVIB,the Xu-Needleman potential [9] is adopted to quantify the strain energy of a bond,which reads

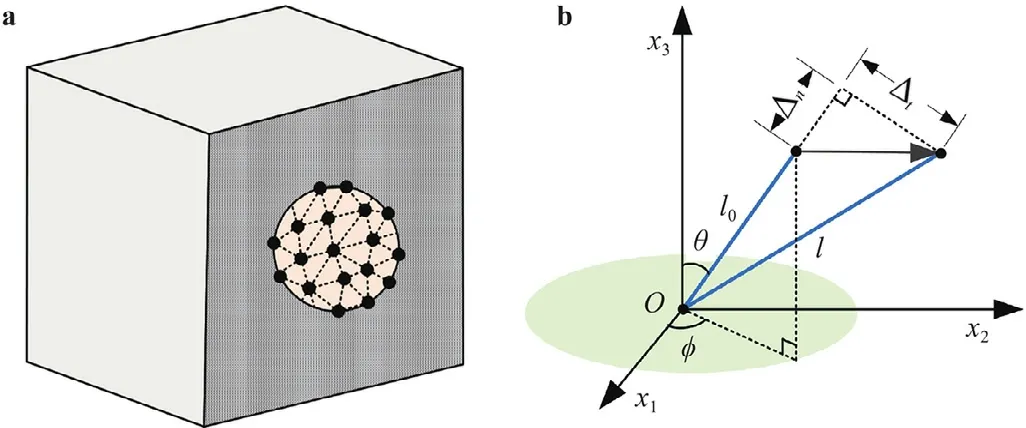
Fig. 1. AVIB model a representative element volume of AVIB and b a bond in the spherical coordinate system.

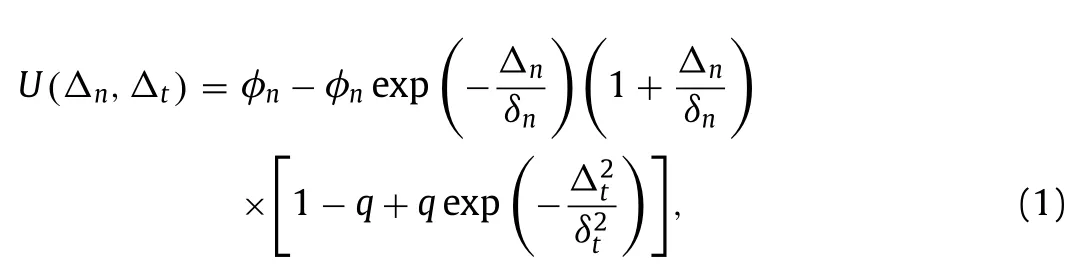
Fig.2. Bedding planes of shale a shale sample and b BPs in local coordinate system.

whereΔn,Δtare the normal and tangent deformation of a bond,respectively;δnandδtare the characteristic lengths for the normal and tangential deformation,δnδtis the strain of bond at the peak uniaxial tensile force,usually takingε˜t≈εtwithεtbeing the strain value at the peak stress of the uniaxial tension stress-strain curve of material;φnstands for the energy related to the normal bond deformation andqthe energy ratio of the normal bond deformation to the tangent one.Their relationship with the macro constants is

whereEis the Young’s modulus,vthe Poisson’s ratio,l0 the undeformed bond length andVthe volume of REV.

According to the Cauchy-Born rule [10],the bond deformations(shown in Fig.1b) are associated with the macro strain tensor by

whereεis the strain tensor of the REV andξthe bond orientation vector,ξ[sinθcosϕ,sinθsinϕ,cosθ]Tin the spherical coordinate system (Fig.1b);the superscript "T" means the transpose.

With Eqs.(1)–(3),the stress tensor of AVIB is derived as

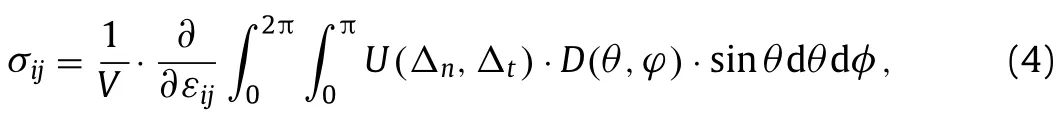
and the tangent modulus tensor is

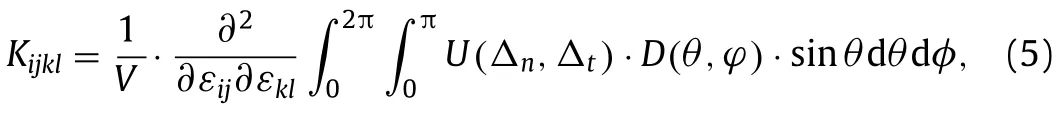
whereD(θ,ϕ)is the bond distribution density in terms of the spherical coordinatesθandϕ.

For a shale which contains numerous BPs,shown in Fig.2,Zhang et al.[6] have established the BP tensor to quantify BP.That is

whereΩis the local BP tensor in the local coordinate of BP,ΩDiag(0,0,ω).ωis a parameter varying from 0 to 1,which reflects the weakening degree of shale stiffness in the normal bedding direction.Qis the global-to-local coordinate transformation matrix

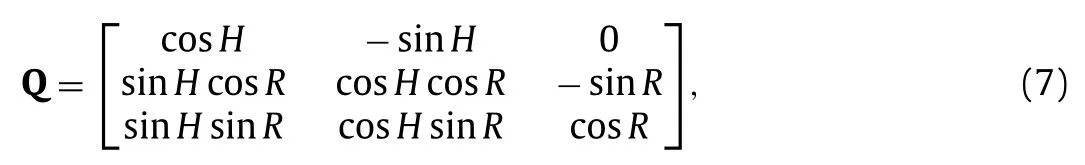
whereHbeing the azimuth andRthe dip angle of BP.

In Ref.[6],the bond distribution density in the directionξis associated with the BP tensor through

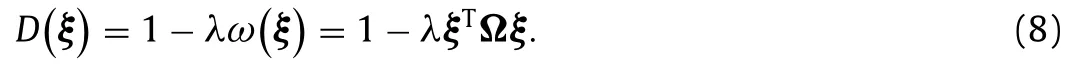
In this letter,the bond distribution density of AVIB is quantified by the same manner.Thus,the constitutive relation of BPembedded AVIB is

whereλis a coefficient to be calibrated in the following context.

To what degree that the BP-embedded AVIB can represent a transverse isotropic solid (TIS) is a key point.It will be discussed in the following.

In the linear elasticity theory,the elastic matrixCof TIS is defined through [σ11,σ22,σ33,σ12,σ23,σ31]TC[ε11,ε22,ε33,γ12,γ23,γ31]T.The elastic matrix is expressed as

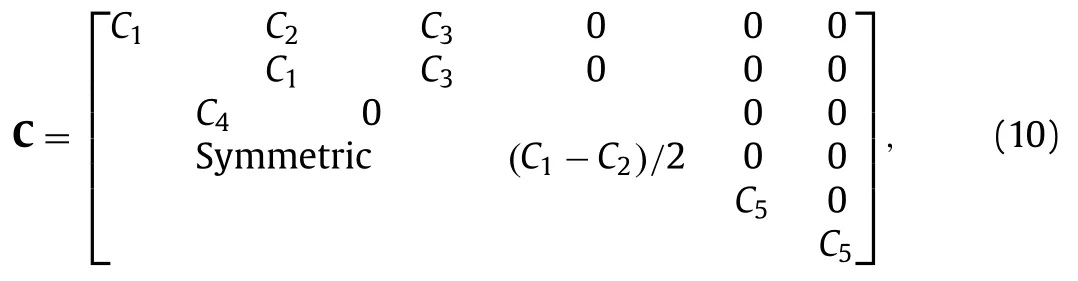
whose components are

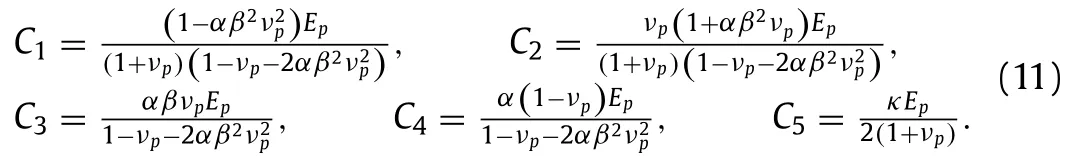
In these components,αEz/Ep,βνpz/νpandκGzp/Gp,whereEpandνpare the Young’s modulus and Poisson’s ratio in thex-ysymmetry plane,respectively;Epzandνpzare those in thez-direction,respectively;Gzpis the shear modulus in thezdirection.For the TIS solid,the relationshipνzp/Ezνpz/Epholds,soνzpαβνp.Therefore,the TIS solid has five independent parameters,i.e.,{Ep,νp,α,β,κ}.

According to Eq.(5),the tangent modulus of AVIB can be derived asKijkl∂σij/∂εkl.At the initial state,i.e.,ε0,the tangent modulus is

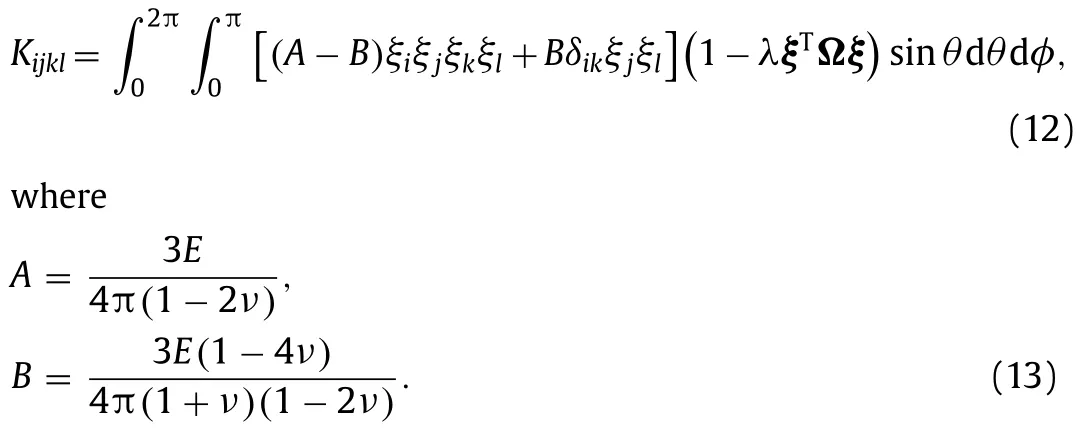
By integrating Eq.(12),the elastic matrixDof AVIB is obtained

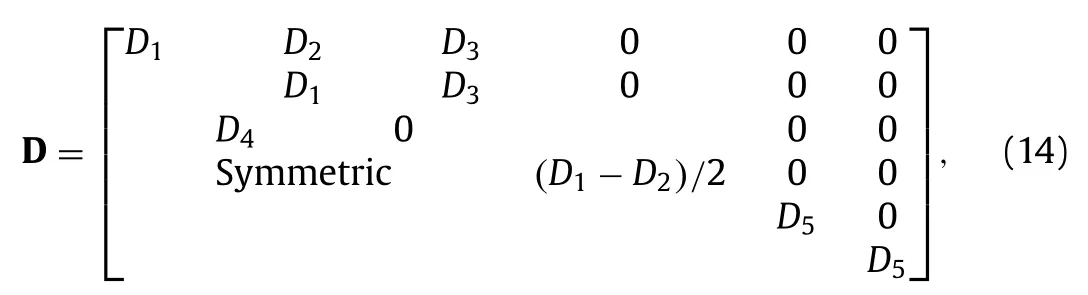
whose components are

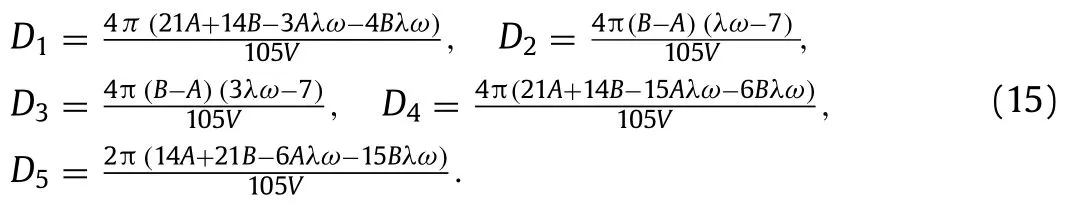
Due to the effect of BP,the weakening degree in the normal direction of BP can be characterized byD4/D1.In the limit case ofω0,D4/D11 holds while in the limit case ofω1,D4/D10 holds.Therefore,the coefficientλis derived as

In Eq.(16),whenv0.25,AVIB is reduced to VIB.Correspondingly,λ|ν0.251.4,which is consistent with that of Ref.[6].

Through the comparison between the two elastic matric,i.e,Eqs.(10) and (14),we can recognize how the AVIB can represent a TIS.At first,the most important feature of the TIS matrix lies in its structure,i.e.From Eq.(14),it is seen that the AVIB possesses the same structural feature.

Next,the diagonal components will be compared.According to the physical meaning ofαandω,we have the following relationship

The stiffness deterioration in the normal direction of BP in AVIB can be expressed by

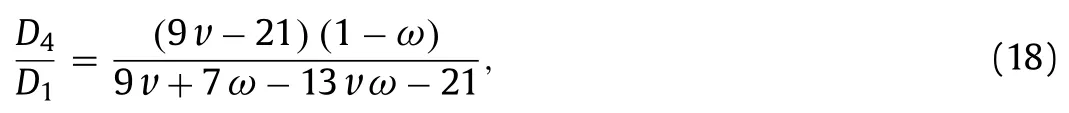
while that in TIS is

According to Eqs.(18) and (19),the stiffness deterioration is shown in Fig.3.It is seen that although Eq.(18) is quite different from Eq.(19) in form,they almost linearly decreases from 1 to 0 withωincreasing.That is,the AVIB and TIS present the same trend.

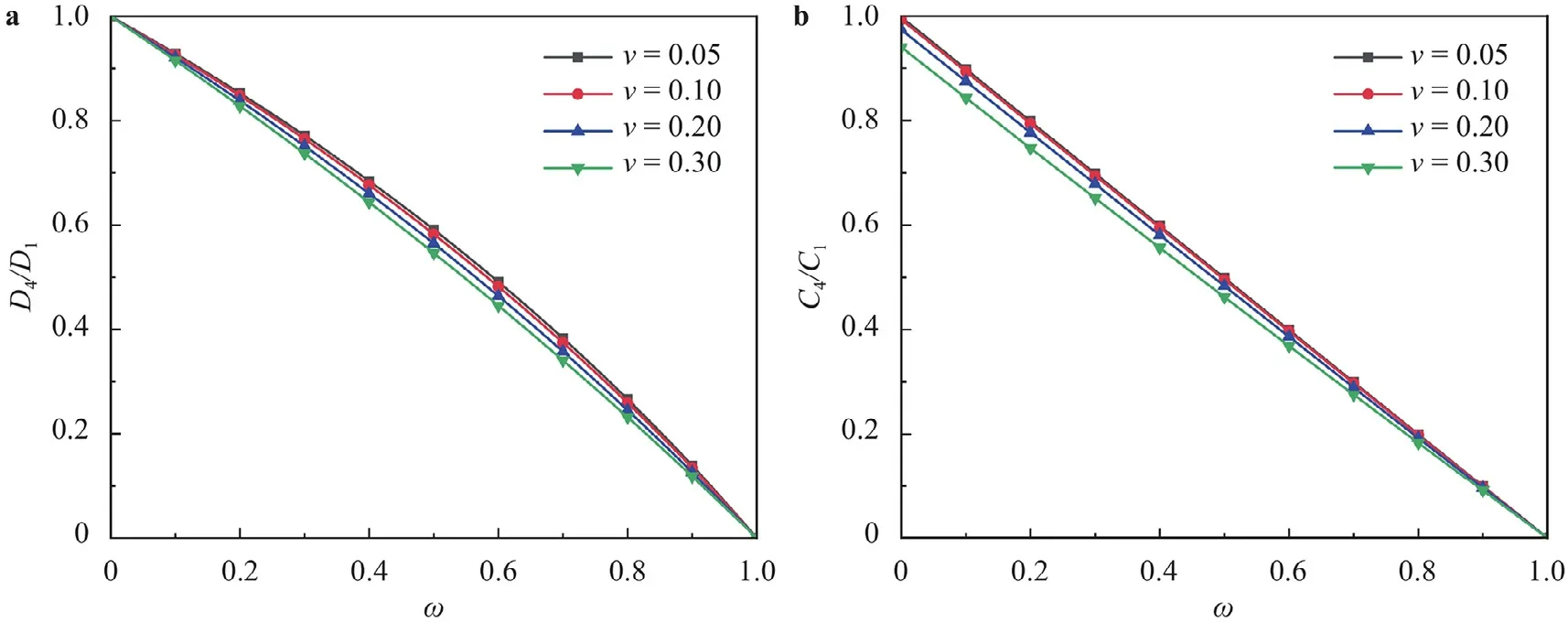
Fig.3. Stiffness deterioration in the normal direction of BP a AVIB and b TIS (β 1.0).

LetDi0 andCi0denote the initial value ofDiandCicorresponding toω0.The influence of BP on the stiffness in orthogonal direction,i.e.,D1/D10andC1/C10,is shown in Fig.4.It is found that the influence of BP on the orthogonal stiffness in AVIB is close to TIS.

Fig.4. Influence of BP on the orthogonal stiffness.

In TIS,κis the ratio of shear modulus in thez-direction to thex-ysymmetry plane,which reflects the deterioration degree of shear modulus with BP.Analogous,in AVIB,κis defined asκD5Giso,whereGisodenotes the shear modulus of isotropic solid,i.e.,GisoE/[2(1+v)].Figure 5 shows the variation ofκwithω.It is seen thatκdecreases from 1.0 to about 0.52 withωincreasing from 0 to 0.5.Hou et al.[11] reported that theκis about 0.58,which falls into the deterioration scope shown in Fig.5.

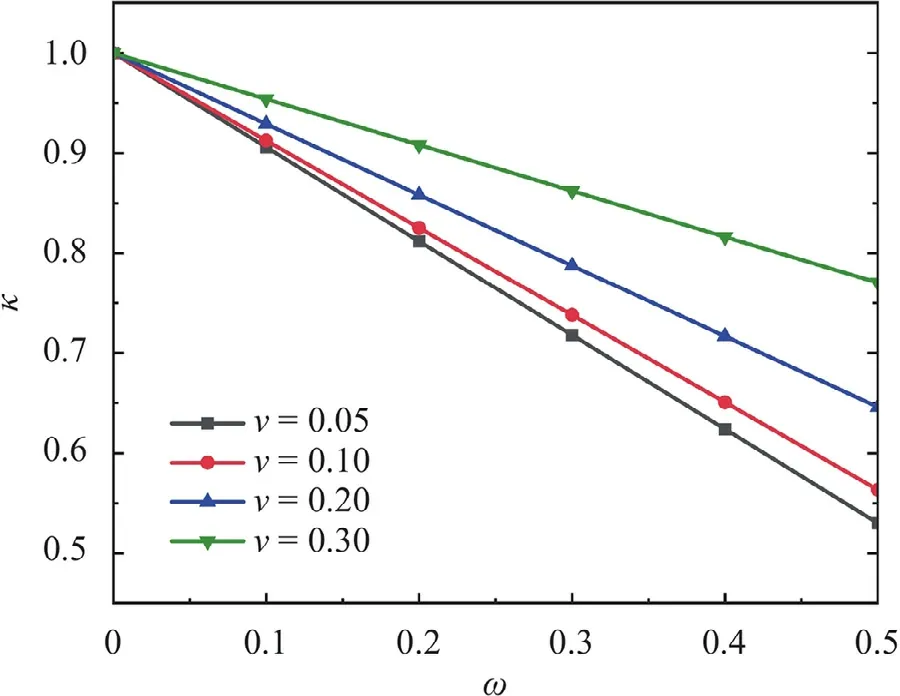
Fig.5. Influence of BP on shear modulus.

TheD2,C2andD3,C3variation with BP are shown in Fig.6.It is seen that the deterioration degrees of off-diagonal components in AVIB and TIS are close.

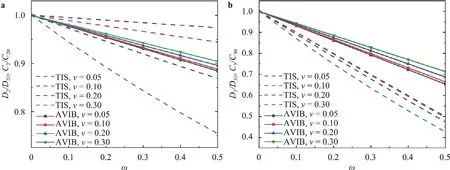
Fig.6. Off-diagonal element variation with BP a D2/D20 and C2/C20 and b D3/D30 and C3/C30.

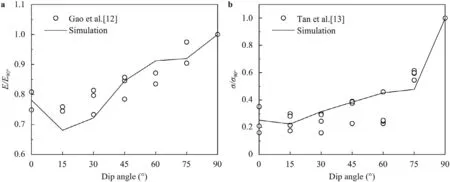
Fig. 7. Comparison between the simulated and experimental results a the simulated and the tested stiffness reported in Ref.[12] and b the simulated and tested tensile strength reported in Ref.[13].

TIS theory has five independent parameters,i.e.,{E,υ,ω,β,κ},while AVIB has three,i.e,{E,υ,ω}.So,AVIB is simpler than the TIS theory although AVIB is not as accurate as TIS in shale description.Compared with the VIB [6],AVIB can account for the Poisson’s ratio.Therefore,it is more accurate than VIB.

In order to examine whether the BP-embedded AVIB can reflect the shale anisotropy induced by BPs,the following simulation examples are conducted.The simulation object is a cubic body with inclined BPs.The simulation parameters are as follows:ω0.5,ρ2400 kg/m3,E40.0 GPa,εt2 × 10−4.

The comparison between the simulated and the experimental results [12,13] is shown in Fig.7.It is seen that the simulation results are in agreement with the tested ones.So,the present model can capture the anisotropy of shale induced by BPs.

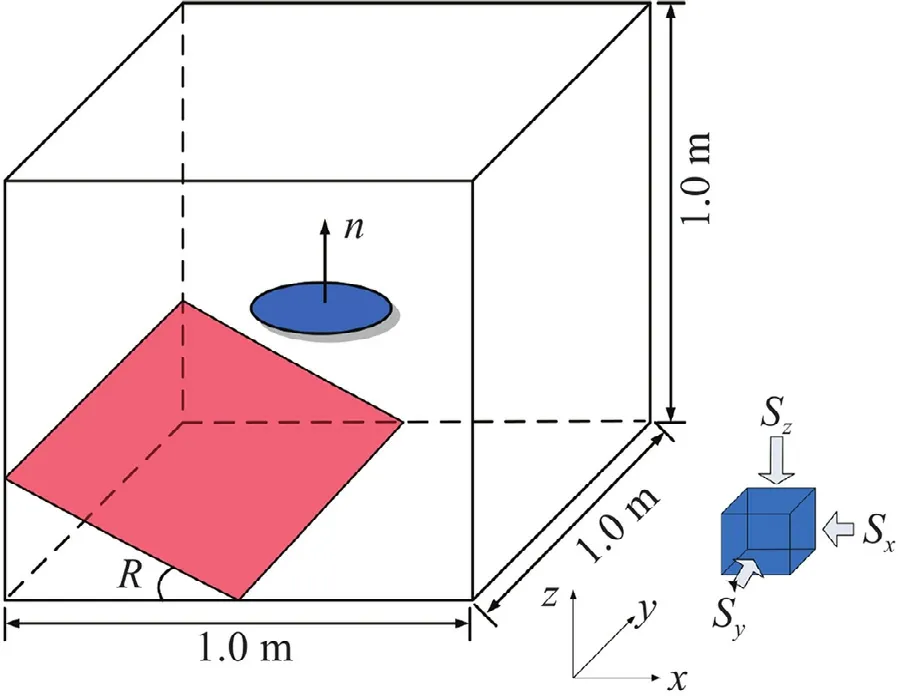
Fig. 8. Simulation object of hydraulic fracture (the red plane represents a bedding plane in the rock).

To examine how the BPs impact the hydraulic fracture,the following cases are simulated.Figure 8 shows the simulation object,a cubic body with a preset penny-shaped crack.The size of the simulation object is 1.0 m × 1.0 m × 1.0 m while the radius of the preset crack is 0.2 m.We set the strike of BP aligning withy-axis and the dip angleR.The principal BP value isω0.5.The simulation is conducted in three cases.In Case-1,there is no BP as the reference case.In Case-2 and Case-3,the dip angle of BP is respectively 30 and 60 degrees.To simulate the fracture propagation,the 3D-EPM[14] is employed here.The simulation parameters are:ρ2,400 kg/m3,E40.0 GPa andν0.25;flux1.5 × 10−7m3/s andμ0.05 Pa.s.The fluid is injected into the preset crack at a constant flux.In addition,to exclude the impact of in-situ stress,the isotropic in-situ stress are set,which areSxSySz5 MPa.

The simulation results of the reference case are shown in Fig.9a.It is seen that the hydraulic fracture propagates in the horizontal direction,which is reasonable in the isotropic in-situ stresses condition with no BPs.When we set BP at dip angle of 30 °,as illustrated in Fig.9b,the hydraulic fracture no longer propagates along the horizontal direction,instead,approaching to the bedding direction.As the BP angle further increased to 60 °,shown in Fig.9c,the hydraulic crack deflects upward more obviously.These suggest that the BP has significant impact on the hydraulic fracture growth direction.Such influence agrees with the observation in the experiment reported in Ref.[15].Comparing the simulated wellbore pressures in the three cases (Fig.10),it is found that the peak wellbore pressure with BP is much lower than that without BP.This is due to the weakening effect of BPs.

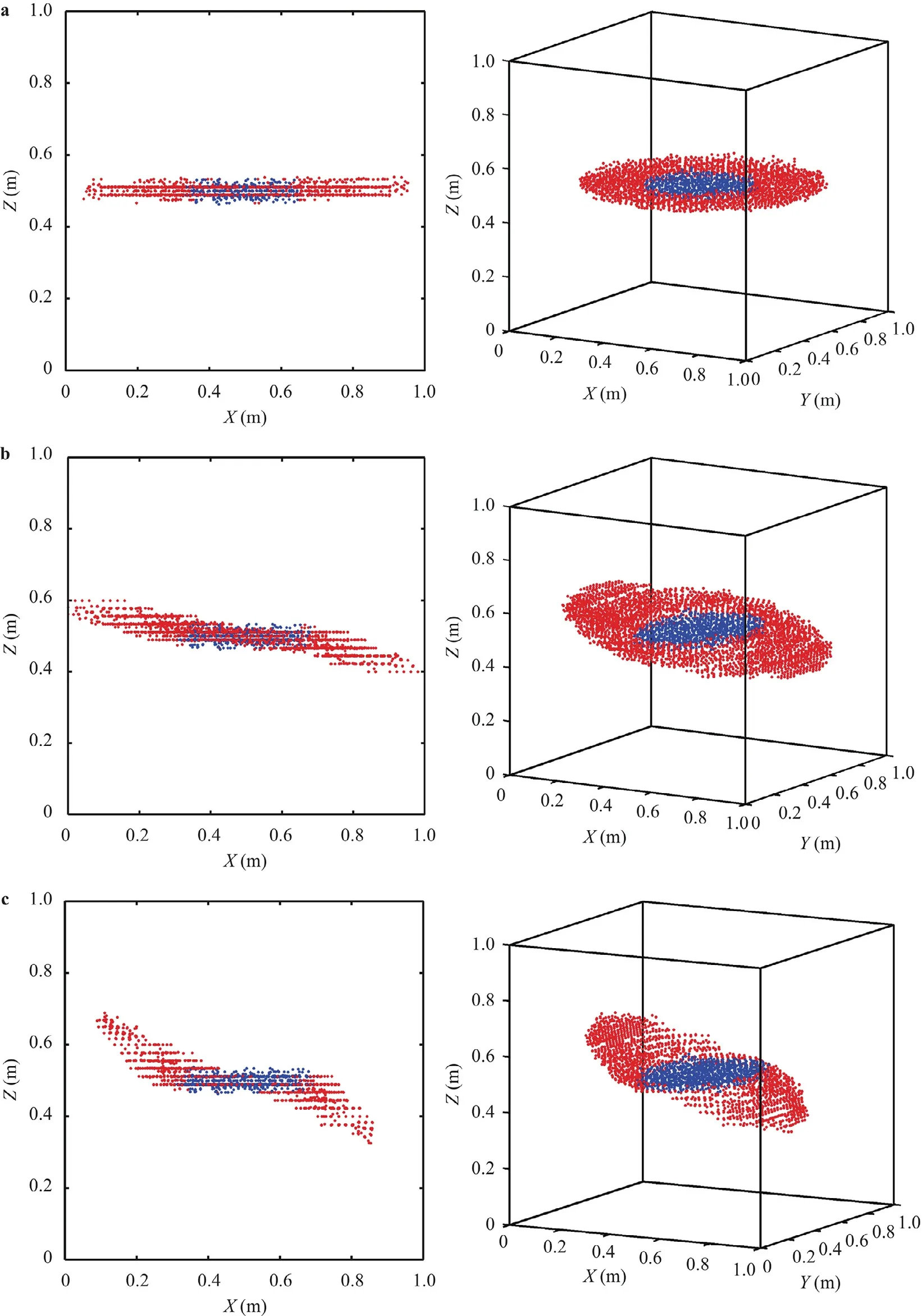
Fig.9. Simulation results of hydraulic fracture. a Case-1, b Case-2, c Case-3.

The bedding plane effect is incorporated into the AVIB through the bedding tensor.By comparison between the BP-embedded AVIB and the transverse isotropic theory,it suggests that such AVIB model can capture the transverse isotropy in theory.The simulation results suggest that this method can simulate the anisotropy of shale induced by BP and it can represent the effect of BP on hydraulic fracture propagation direction in shale.This study provides a new constitutive relation approach to simulate fracture propagation in rock with consideration of bedding plane effect.

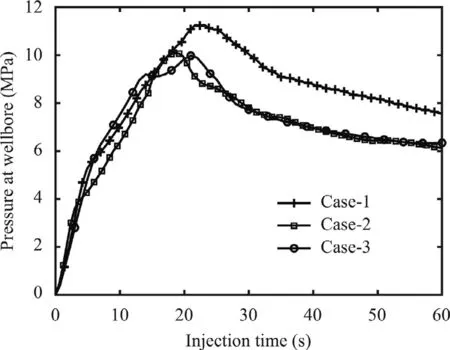
Fig.10. Simulated wellbore pressure versus time.

DeclarationofCompetingInterest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgment

This work is supported by the National Natural Science Foundation of China (Grant 11772190),which is gratefully acknowledged.