Analytical and numerical studies for seiches in a closed basin with various geometric shapes of longitudinal section
2021-08-14MagdalenaKarimaRifatin
I.Magdalena ,N.Karima,H.Q.Rif’atin
Faculty of Mathematics and Natural Sciences, Bandung Institute of Technology, Bandung, Indonesia
Keywords:Seiches Fundamental resonant period Closed basin Shallow water equations Finite volume method
ABSTRACT Seiches are long-period standing waves with a unique period called a natural resonant period,during which the phenomenon of resonance occurs.The occurrence of resonance in coastal areas can cause destruction to surrounding natural and man-made structures.By determining the resonant period of a given basin,we can pinpoint the conditions that allow waves to achieve resonance.In this study,a mathematical model is developed from the shallow water equations to examine seiches and resonances in various types of closed basin.The developed model is solved analytically using the separation of variables method to determine the seiches’ fundamental resonant periods.Comparisons between the analytical solutions and experimental measurements for resonant periods are also provided.It is shown that the analytical resonant period confirms the experimental data for closed basin of various geometric profiles.Using a finite volume method on a staggered grid,the model is solved numerically to simulate the wave profile when resonance phenomenon occurs.Through those numerical simulations,we also obtain the fundamental resonant period for each basin which agrees with the derived analytical period.
Oscillation phenomena can occur in many dynamical systems,including the system of wave motions in a basin.One of the common examples of free oscillation is a seiche,a long-period standing wave in a closed or in a locally isolated basin.Seiches can be triggered by various external forces such as seismic and atmospheric pressure disturbances,wind,or internal and surface gravity waves [ 1,2 ].This phenomenon is first accurately observed at Lake Geneva in 1730 by Fatio de Duillier,as mentioned in Ref.[3] .It is described as the rocking motions of the surface of a body of water after it has been disturbed,as the body of water gradually returns to its original,undisturbed condition.These oscillations occur at a unique period called the natural (resonant) period,which is heavily influenced by the geometric shape and configuration of the basin holding the body of water in question.Resonance occurs when the period of the wave generated by external forces matches the basin’s natural period.Wave resonances are physically indicated by the amplified wave height at the basin’s boundary.If the wave height at the boundary is large enough,this occurrence will cause destruction to the environment around the basin.It can damage moored ships in harbors or ports,coastline structures,and may also result in coastal flooding of lowland areas [4] .Sometimes,the energy produced by resonant waves are even larger than those of extreme tidal phenomena [5] .
Considering the disadvantageous effects described above,it is important to know the resonant period of given basins,which will allow us to estimate when resonance is likely to occur.Several analytical and numerical studies have been conducted to determine the resonant period for simpler geometric shapes such as rectangular,triangular,and parabolic closed basins [6–8] .This topic is then extended by Magdalena et al.[9] to evaluate the resonant periods over rectangular,triangular,and parabolic closed basins by taking the bottom friction into consideration.The findings of this study show that,for any type of bottom topography,the formula used to calculate the value of the resonant period with bottom friction is the same,which isωfwhereωfis the resonant frequency with bottom friction,Cfdenotes the friction coefficient,andω0represents the resonant frequency without bottom friction.This formula is claimed to be applicable to any shape of closed basin,including the more complicated ones.It means that the resonant period of any type of basin with bottom friction can be easily determined as long as the resonant frequency (period) in case of friction-less bottom topography has been achieved.However,for basins of more complicated shape,analytical approach to obtain the friction-less resonant period is rarely found.Instead,most researchers use an experimental approach to find the resonant period [10–13].However,physical models are costly to set up and require longer observation time.Moreover,a different experiment must be conducted for different basin type.In the interest of conserving resources and expanding our previous researches in Refs.[6,7,9],we aim to derive the analytical fundamental resonant period for more complicated geometric shapes,particularly triangular(right-angled),trapezoidal,and coupled rectangular closed basins.These configurations have been used in the experiments done in Ref.[10].Here,the linear shallow water equations will be solved analytically using separation of variables and numerically using the finite volume method on a staggered grid.The use of separation of variables to solve the linear shallow water equations analytically was also done to observe wave propagation over a twodimensional shallow shelf [14].The finite volume on a staggered grid method for solving linear shallow water equations numerically is presented in Refs.[15–17] where the numerical scheme was tested on various dam break cases.Particularly in the computational part of this research,all the parameters and the set-up of the basins are specifically defined to follow the shallow water condition,which iskH<Π/10.Since the simulations conducted under the assumption of shallow water region,the waves that will be simulated are considered to be non-dispersive waves.Moreover,after solving the equations,we will compare our analytical and numerical fundamental resonant periods against experimental measurements in order to analyze the accuracy of both models.In this case,we limit our problem by assuming that the width of each basin is constant and there is no friction effect involved.The effect of varying width and constant topography to the wave oscillation has been investigated in Refs.[18],whereas cases with porous media and bottom friction were studied in Refs.[6,9,19,20].
Here,we consider an oscillation that occurs after an external force acts on the basin as illustrated in Fig.1.The fluid moves with horizontal velocityu(x,t) which is assumed to be uniform along thez-axis.To observe the wave propagation over the basin with depthhη+d,we use linear shallow water equations as follows:

Fig.1. Problem description.

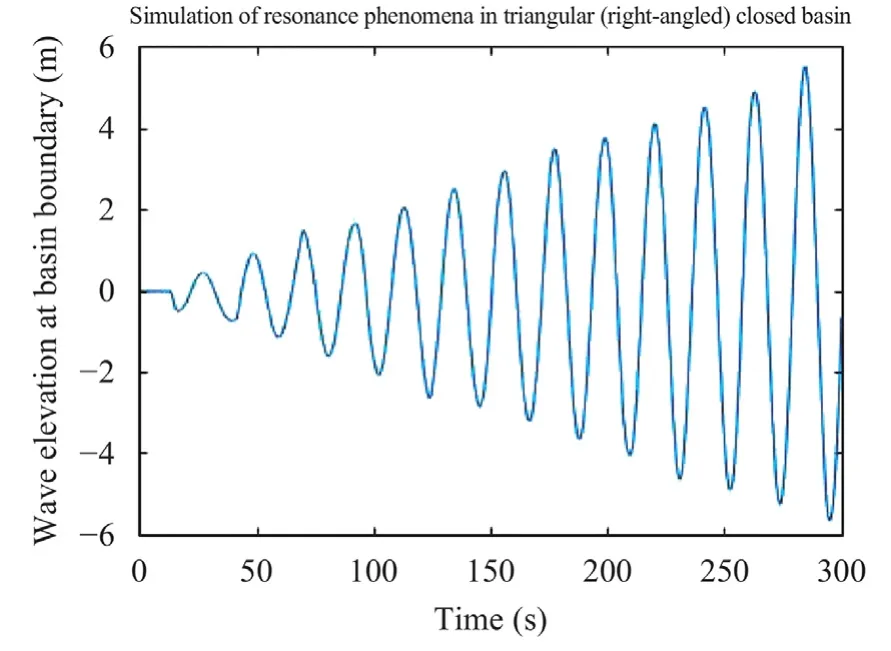
The equations are derived from two physical principles,namely the conservation of mass and conservation of linear momentum.The gravitational acceleration is taken to beg9.81 m/s2.The symbolη(x,t) denotes the surface elevation.Since we assume thatη < In this paper we study closed basins of three geometric shapes: 1 Triangular (right-angled) basin withh(x)in domain 0 ≤x≤L; 2 Trapezoidal basin withh(x)h0+in domain 0 ≤x≤L; Fig.2. Triangular (right-angled) closed basin. 3 Coupled rectangular basin withh(x)h1in domain −L1≤x≤0 andh(x)h2in domain 0 whereh0,h1,andh2are constants that represent the minimum or maximum water depth in a basin with lengthL(m). Next,the analytical solution of the linear shallow water equations will be derived using the separation of variables method.The obtained solution will then be used to find the fundamental resonant period,which is the largest resonant period of the seiches being studied,of a certain basin.To find the solution,first,we assume that the functionsη(x,t) andu(x,t) are monochromatic wave functions where in whichFandGare certain functions ofx,whileωis a constant angular frequency. Then,by substituting Eqs.(3) and (4) to Eqs.(1) and (2),we find the following second-order ordinary differential equation: in which the functionG(x) can be written as follows: Equations (5) and (6) are the essential equations that will be used to derive the analytical solution for each type of basin. Now,we will determine the analytical solution for each basin type,starting with the triangular (right-angled) closed basin.This type of basin has a depth ofh(x)in the domain [0,L].Substituting the formula ofh(x) to Eq.(5),yields Considering that the basin is closed,as shown in Fig.2,then we can define the boundary conditions of the model as hard-wall at both sides or atx0 andxL,according to the domain description.In mathematical terms,the boundary conditions can be rewritten asu(0,t)u(L,t)0.From Eqs.(4) and (6),we can rewrite the boundary conditions as whereC1andC2are constants.The function Jn(x) and Yn(x) are the first and second-kind Bessel functions of ordern,respectively.Taking the derivative of Eq.(10),we have By substituting Eq.(8) to Eq.(11),we obtain Based on their characteristics,the values of the first order Bessel Function of the first and second kind can be approximated by J1(0) ≈0 and Y1(0) ≈−∞,respectively.Therefore,Eq.(12) is satisfied if and only ifC20. Further,from Eq.(9) and the conditionC20,we find To derive the fundamental resonant period of this basin from Eq.(13),we take the first root of functionbased on the Wolfram language,which is 3.8317.Hence,we have3.8317,whereωandT1is the fundamental resonant period of the basin, The second type of basin is the trapezoidal basin,which has similar shape and domain with the triangular (right-angled) as confirmed by Fig.3.Thus,the boundary conditions used here are the same as those mentioned in Eqs.(8) and (9).However,the depth formula is slightly different from that of the triangular basin.The depth of the basin’s left side is represented by the constanth0and that of the right side is denoted byh1.Therefore,we can write the formula of the basin depth ash(x)h0+In this study,we consider three different depth configurations:We will investigate the fundamental resonant period for each configuration.With respect to the first configuration,Eq.(5) can be written as Fig.3. Trapezoidal closed basin. which has the solution whereC3andC4are constants.Notice that we also obtain Bessel Functions of the first and second kind in the solution,as we did in the previous solution.The first derivative ofFwith respect toxis From the boundary conditions,we have a system of equations consisting of Using the elimination method,we removedC4from the system of equations.Note thatC30 must be satisfied forF(x) to be a nontrivial solution.Therefore,we have which is satisfied when From Eq.(21),we obtain the fundamental resonant period for a trapezoidal closed basin withwhich is The trapezoidal closed basin with depth ratios ofandare treated exactly the same way as the basin with a depth ratio ofdespite difference inF(x) andFx(x).The fundamental resonant periods for the other two configurations are presented in Table 1. Table 1 Comparisons of the analytical solution and experimental data of fundamental resonant period of each closed basin. The last basin type to be discussed is the coupled rectangular as illustrated in Fig.4.It has a finite step as its bottom topography with the form of a rectangular basin.Its depth formula is written as Fig.4. Coupled rectangular closed basin. Substitutingh(x) and Eq.(24) to Eq.(5) gives us a piece-wise second-order ordinary differential equation written as with boundary conditions defined as However,to determine the fundamental resonant period of this basin,we have to consider another condition,which is the positioning of nodal lines in a closed basin [11].For the fundamentalmode,it is stated thatη(0,t)0 need to be satisfied.Therefore,we have The solution of Eq.(25) can be written as whereA,B,C,andDare certain constants.Now,we need to make sure thatF(x) is continuous atx0 by following the matching conditions [12],which are From the first matching condition,we find thatACmust be satisfied,while the second condition gives usD.Thus,Eq.(29) can be rewritten as and its first derivative with respect toxis The fundamental resonant period of this type of basin will be derived for four different configurations ofL1andL2,namelyand.For the first configuration,which iswe substitute the length ratio along with Eq.(28) to Eq.(32),resulting inA0 no matter which equation that is used.After that,we substitute Eq.(26) andA0 to Eq.(33) which gives us two possible solutions,which areB0 orChoosingB0 results in a trivial solution ofF(x).Therefore,we choose withB0.Hence,we have The fundamental resonant period is obtained whenn1 and therefore yields the following result whereT1is the sought period.The exact same procedure is applied to find the fundamental resonant period for the other three length ratios.The solutions obtained from this process alongside with the other analytically obtained fundamental resonant periods are presented and compared to the experimental data measured by Wilson [10] in Table 1.Unfortunately,there are several cases where the experimental data are not available.In Table 1,the relative errors are calculated using the formula ofrelativeer-Overall,the relative errors are quite small,which means that our model approximates the experimental data very well. Table 2 Comparison of the analytical and numerical fundamental resonant period in the triangular (right-angled),trapezoidal,and coupled rectangular basins obtained for parameters Ltotal 25 m, hmaximum 1.5 m,and g 9.81 m/s2. Table 2 Comparison of the analytical and numerical fundamental resonant period in the triangular (right-angled),trapezoidal,and coupled rectangular basins obtained for parameters Ltotal 25 m, hmaximum 1.5 m,and g 9.81 m/s2. Further,we will solve the linear shallow water equations numerically in order to simulate wave propagation when resonance occurs and obtain the fundamental resonant period.The numerical scheme is derived by stressing the equivalence of a leapfrog method for linear shallow water equations to the finite volume method on a staggered grid [21].Consider a domain [0,L]which is partitioned into a staggered grid with the labels0,x1,···,···,L.Here,we store the value ofuonly at the half-grid points,whilst the full-grid points store values ofηandh. In the finite volume method,the linear shallow water equations are approximated using a fixed volume called a cell.As illustrated in Fig.5,the mass conservation equation (Eq.(1)) is approximated on cells which have their centers located at full-grid points.The cells labeled [xj,xj+1],with the half-grid points at their centers,are used to approximate the momentum balance equation (Eq.(2)).Thus,the full numerical scheme is presented below: where Regarding the stability of the numerical scheme,we use the Courant–Friedrichs–Lewy stability condition which is derived using Von Neumann stability analysis,guaranteeing Fig.5. Staggered grid illustration. Next,the numerical scheme which consists of Eqs.(37)–(39)will be applied to simulate resonance in a closed basin with several different shapes and to find the numerical resonant period of each basin.We will conduct several numerical simulations with various time observations depending on the shape of the basin,in the range of [200,500] seconds,so that the resonance phenomenon in each basin can be studied accordingly.The initial conditions that will be used in the simulations areη(x,0)0 andu(x,0)0 for all kinds of basins.They represent the condition of an undisturbed body of water.For the boundary conditions,we will use the same conditions mentioned previously for all types of basin.The computational scheme is computed for a total basin length ofL25 m which will be divided into partitions measuring Δx0.1 m in length.The maximum depth used isH1.5 m.All those parameters are defined specifically to satisfy the conditions of shallow water waves,which iskH<Π/10,wherekis the wave number,obtained from the dispersion relation of the linear shallow water equations,k[14].To verify that all the parameters fulfill the shallow water condition in every type of basin,we take the analytical resonant period of each basin and substituting the parameters to those periods.We found that the value ofkHin each basin is in the range of 0.1150 ≤kH≤0.1857,which is much smaller thanΠ/100.3142.This implies that our simulations are under the assumption of shallow water domain which means that the waves that are about to be simulated are non-dispersive waves.Thus,all the results to be obtained in this simulation,including the numerical resonant periods and the resonant wave profiles,are free from dispersive effect. Previously,we have obtained the fundamental resonant period for each shape of basin.Here,we calculate the resonant periods numerically and compare them to the analytical solutions later on.The numerical fundamental resonant period is computed using a trial and error procedure involving the simulation of severalT1 values for each basin in order to find those which give rise to resonance.Physically,continuous increases of wave amplitude indicate the presence of resonance.Comparisons between the analytical solutions and numerical results for the fundamental resonant periods with the mentioned parameters are presented in Table 2.Figures 6–8 illustrate the resonance phenomena with corresponding periods for triangular (right-angled),trapezoidal,and coupled rectangular closed basins,respectively. From Table 2,we can see that the relative errors between the analytical and numerical fundamental resonant periods do not exceed 0.5%.This result indicates that our numerical scheme has approximated the analytical model accurately.Considering that our analytical solutions have confirmed the experimental results,it means that all three approaches are in a strong agreement with each other.In addition,Figs.6–8 show how the waves will behave if resonance occurs.As expected,the wave elevation in every basin type increases with time.Notice that for the trapezoidal basin in Fig.7,the wave amplitude at every peak point decreases with the basin’s depth ratio.It means,as the profile of the basin becomes more rectangular than triangular,the amplitude of the waves will grow larger at every peak point.This result is similar to the result presented in Refs.[6,7].However,in the case of the coupled rectangular basin presented in Fig.8,the same conclusion cannot be drawn,since the wave amplitude at every peak is independent of the length ratio. Fig.6. Resonance phenomena in triangular (right-angled) closed basin. Fig.7. Resonance phenomena in trapezoidal closed basin. Fig.8. Resonance phenomena in coupled rectangular closed basin. In conclusion,we have successfully determined the analytical and numerical fundamental resonant periods of seiches in triangular (right-angled),trapezoidal,and coupled rectangular closed basin using a model that is developed from the linear shallow water equations.Analytically,the model is solved using separation of variables,while numerically,it is solved using finite volume method on a staggered grid.The obtained analytical and numerical fundamental resonant periods confirm the experimental results in Refs.[10–12] with relatively small errors of less than 2%.Furthermore,in the numerical simulations for the trapezoidal closed basin,there is a positive correlation between the ratio of basin side depth and the maximum surface elevation.The smaller the ratio,the smaller the wave amplitude.On the other hand,for the coupled rectangular type,the maximum surface elevation is independent from the length ratio. Acknowledgement This work was supported by the ITB Research Grant.












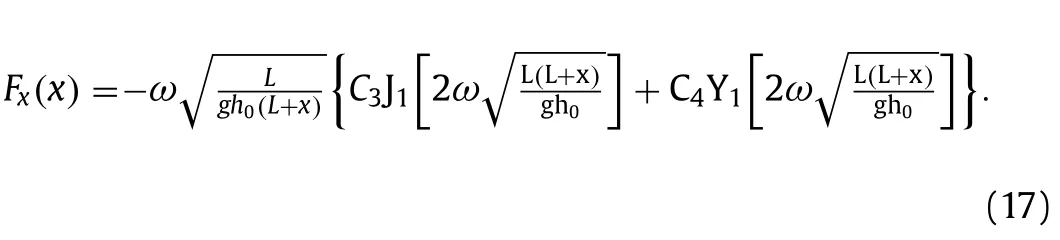








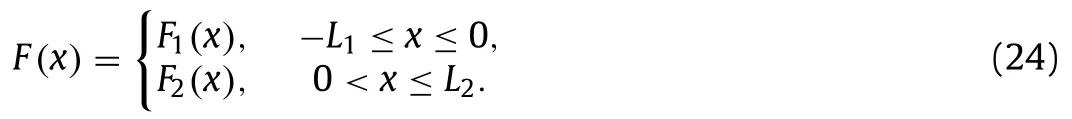






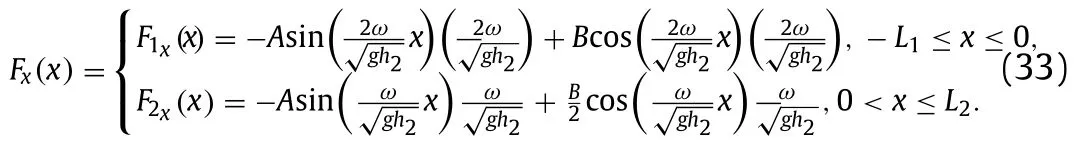









杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- A geometry-based framework for modeling the complexity of origami folding
- Why neural networks apply to scientific computing?
- Analytical solutions for inflation of pre-stretched elastomeric circular membranes under uniform pressure
- Computing mean fields with known Reynolds stresses at steady state
- Fundamental kinematics laws of interstitial fluid flows on vascular walls
- Effect of interfacial stiffness on the stretchability of metal/elastomer bilayers under in-plane biaxial tension
