Analytical solutions for inflation of pre-stretched elastomeric circular membranes under uniform pressure

Jinghong Yun ,Xinlin Liu ,Hiin Xi ,Yin Hung

a Applied Mechanics and Structure Safety Key Laboratory of Sichuan Province, School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China

b Key Laboratory of Advanced Technologies of Materials, Ministry of Education, School of Materials Science and Engineering, Southwest Jiaotong University,Chengdu 610031, China

Keywords:Elastomeric circular membrane Inflation and deflation Nonlinearity Analytical solution Quantitative design

ABSTRACT Elastomeric membranes are frequently used in several emerging fields such as soft robotics and flexible electronics.For convenience of the structural design,it is very attractive to find simple analytical solutions to well describe their elastic deformations in response to external loadings.However,both the material/geometrical nonlinearity and the deformation inhomogeneity due to boundary constraints make it much challenging to get an exact analytical solution.In this paper,we focus on the inflation of a prestretched elastomeric circular membrane under uniform pressure,and derive an approximate analytical solution of the pressure–volume curve based upon a reasonable assumption on the shape of the inflated membrane.Such an explicit expression enables us to quantitatively design the material and geometrical parameters of the pre-stretched membrane to generate a target pressure–volume curve with prescribed peak point and initial slope.This work would be of help in the simplified mechanical design of structures involving elastomeric membranes.

Elastomeric membranes are commonly used in several emerging fields such as soft robotics [1–6] and flexible electronics [7–10] due to their large deformability and superior resistance to fracture.Representative examples include dielectric elastomer actuators [ 1–5,9,11–13 ],fluid driven soft robots/actuators [6],ionic skins [8],microfluid circuits and electronics [14],and bio-inspired flexible and stretchable electronic eye camera [15] .Motivated by so many important applications,a simple and efficient quantitative design is undoubtedly helpful for the elastomeric membrane structures to achieve desired functionalities and optimized performances.For the sake of convenience in the design process,it becomes very attractive to find simple analytical solutions for elastomeric membranes to well describe their elastic deformations in response to external loadings.

Large deformations of elastomeric membranes are generally inhomogeneous and accompanied with strong material and geometrical nonlinearities,which make it much challenging to get an exact analytical solution [16] .Many researchers work on this topic and some achievements have been made in the past few years.Where the numerical approach is concerned,DasGupta et al.[ 16–18 ] analyzed the static and dynamic axisymmetric inflation of an initially stretched flat circular hyperelastic membrane composed of Mooney–Rivlin solids by solving a two-point boundary value problem numerically.Li et al.[19] numerically solved the pneumatic inflation of a pre-stretched dielectric elastomeric membrane under high voltages based on the Gent model by means of the shooting method.Wang et al.[20] proposed a shooting-method based computational model for the hydrostatically coupled dielectric elastomer actuator consisting of two membranes clamped with rigid circular rings.

As for analytical approaches,by assuming a linear stress-strain relation,Yang et al.[21] and Coelho et al.[22] obtained the analytical solutions for the axisymmetric deformation of circular thin polymer films under gas pressure by using the method of power series,and Li et al.[23] used the same method to solve the large deformation of prestressed circular membranes under uniform lateral loads.Lim [24] presented semi-empirical formulas for the large deflection of circular auxetic membranes with negative Poisson’s ratios under uniform load.Jin and Wang [25] derived exact solutions for large deflection of thin circular membranes with residual stresses under a central point force with two types of boundary conditions.Jin et al.[26] provided analytical solutions for the problem of spherical indentation of a freestanding circular membrane.

In this paper,the inflation of a pre-stretched elastomeric circular membrane under uniform pressure is studied analytically with the aid of a reasonable assumption,adopted and verified by Duan et al.[27] in the case without pre-stretch,that the profile of the inflated membrane can always be approximated by some spherical cap.Under this approximation,the pressure–volume curve of the pre-stretched membrane can be expressed by an explicit formula,based on which we are able to quantitatively design the material and geometrical parameters of the pre-stretched membrane to generate a target pressure–volume curve with prescribed peak point and initial slope.

The circular thin membrane considered in this paper is composed of incompressible,homogeneous and isotropic hyperelastic materials.This membrane is originally flat in the natural state with a radius ofR0,a thickness oft0 and thus an initial surface areaS0(),as shown in Fig.1a and b.It is then equi-biaxially pre-stretched in plane with a stretching ratio ofλ0,after which the radius,thickness and surface area of the flat membrane are changed to beR1(λ0R0),t1(Λ0t0)andS1(),respectively,as shown in Fig.1c,withΛ0from the incompressibility condition.

Fig. 1. Sketches of the elastomeric circular membrane a, b in the natural state,c after pre-stretching,and d under inflation,and e the force analysis of an infinitesimal surface element cutting from the inflated membrane.

Next,by fixing the pre-stretched membrane at its rim,the membrane is then subjected to a“uniform”pressurePover its entire inner surface,under which it is inflated into a rotationally symmetric curved surface with a surface area ofSand an enclosed volume ofV.Note that,during the inflation process,the“uniform”pressure is always normal to the membrane surface.Since the membrane is very thin and soft,the bending rigidity of the membrane is assumed to be neglected and thus it only has an in-plane tensile rigidity.For the sake of further simplification,we make another assumption on the shape of the inflated membrane.Here,it is assumed that the profile of the inflated membrane under pressurePcan be approximated by a spherical cap of radiusRand heightHwith a uniform thickness oft(Λt1),as shown in Fig.1d.Under this approximation,the elastomeric membrane will undergo equi-biaxial stretching during the inflation process,which significantly simplifies the mechanical analysis.The validity of the above approximation will be verified later.

The main objective of this paper is to derive an approximate analytical solution for the pressure–volume curve (i.e.theP−Vcurve) of the pre-stretched elastomeric circular membrane,and further utilize it to perform a quantitative design of membrane structures.This will be achieved next.

Following the spherical-cap approximation,we consider an arbitrary infinitesimal surface element dAof circular shape with a conical angle of dϕon the spherical cap,as shown in Fig.1e.According to the force equilibrium in the normal direction,we have

and it is further obtained that

whereσis the in-plane equi-biaxial Cauchy stress in the inflated membrane of spherical-cap shape.

As shown in Fig.1d,the surface area of the spherical cap can be expressed as

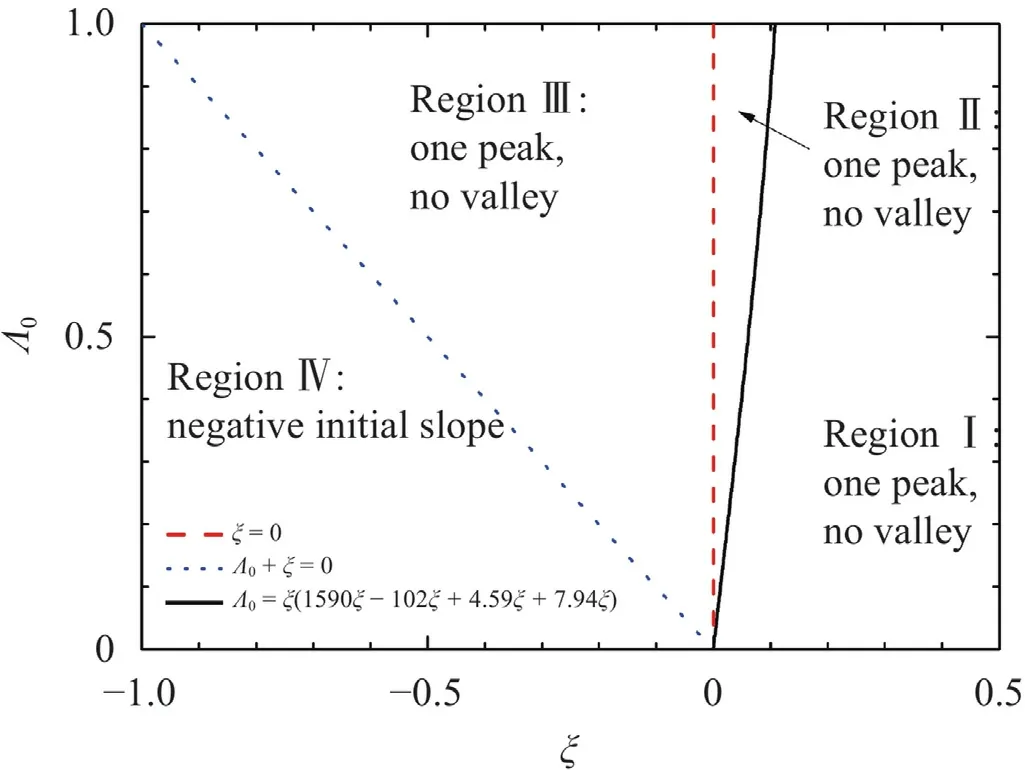
Fig. 2. Phase diagram of the pressure–volume curve with respect to Λ0 and ξ for the total number of stational points.

withS(R,H)+S(R,2R−H)4πR2.

Also,the volume enclosed by the surface and the base of the spherical cap can be expressed as

withV(R,H)+V(R,2R−H)4πR3/3.

In fact,the geometrical parametersRandHof the spherical cap can be expressed in terms of its base radiusR1(λ0R0)by introducing the polar angleθ(i.e.the angle between the ray from the center of the sphere to the apex of the cap and the rim of the base of the cap)

with 0 ≤θ≤π.

By substituting Eq.(5) into Eq.(4),we have

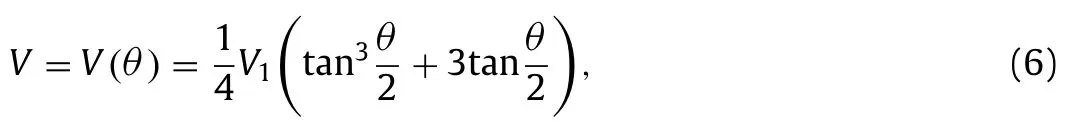
withV1Obviously,Vis a monotonically increasing function ofθ.We further observe that tan(θ/2)can be considered as the unique positive root of the following cubic equation

since −4V/V1<0 and the discriminant of the above cubic equation(2V/V1)2+1>0 (indicating that only one root is real-valued and the other two roots are complex conjugate to each other).According to the well-known Cardano’s formula,the unique positive root of Eq.(7) can be expressed as

which indicates that,once the volumeVis given,the polar angleθcan be calculated analytically.

Moreover,the surface area of the spherical cap can be rewritten as

withS1.Since the elastomeric material is assumed to be incompressible,we have the simple relationStS1t1.This gives

which further leads to

By substituting the first of Eq.(12) into Eq.(2),we can obtain that

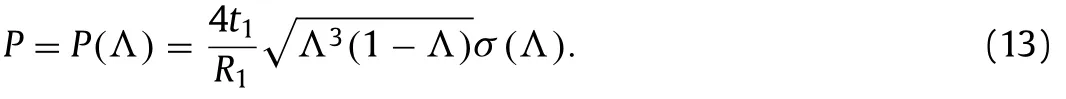
The above equation is applicable for any incompressible elastomeric material.Without loss of generality,we consider the wellknown Mooney–Rivlin solid in the following paragraph.

For incompressible Mooney–Rivlin solids,the relation between the equi-biaxial Cauchy stressσand in-plane stretch ratioλwith respect to the natural state can be expressed as [28,29]

in whichC1andC2are two material constants satisfyingG2(C1+C2),withGbeing the initial shear modulus.For classical materials,the relationG≥0 should be satisfied,which means−1.

The stretching ratio in thickness with respect to the natural state,λ3,is related to the in-plane stretching ratioλby the incompressibility condition as

According to Eq.(15),Eq.(14) can be rewritten as

By substituting Eq.(16) into Eq.(13) and taking Eq.(15) into consideration,we can obtain that

Meanwhile,Combination of Eq.(10) with Eq.(8) leads to

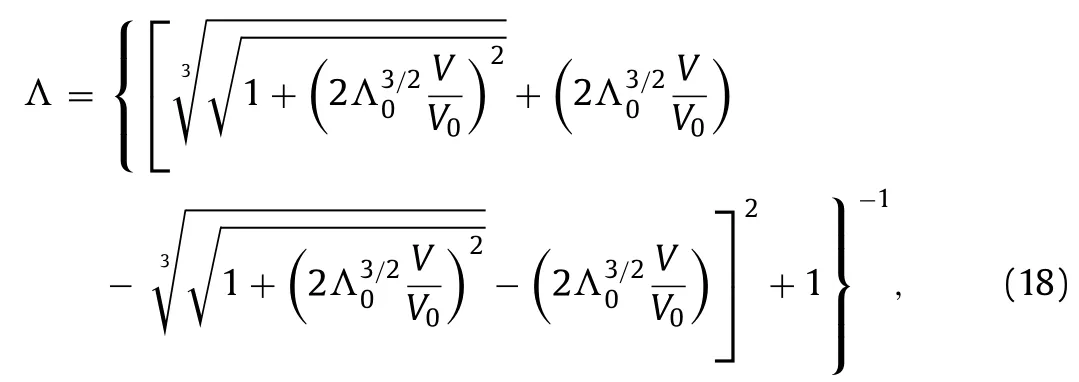
withV0

Substituting Eq.(18) into Eq.(17),we finally obtain the explicit analytical expression of the so-called pressure–volume curve.

Next,we will study the basic properties of the derived pressure–volume curve.

The initial slope of the pressure–volume curve at zero volume can be expressed as

Since 0 ≤Λ0≤1,Eq.(19) indicates that the sign of the initial slope is the same as the sign of the value(Λ0+ξ).Moreover,the initial curvature of the pressure–volume curve at zero volume proves to be identically zero.

Since the volumeVis a monotonic function ofΛ,the stationary points of the pressure–volume curve can be simply determined by0 from Eq.(13) or Eq.(17) as

After simplification,Eq.(20b) can be transformed to a quintic equation below

Obviously,whenξ0 for the particular case of Neo-Hookean solids,Eq.(21) reduced to a quartic equation below

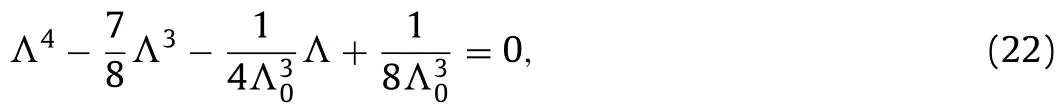
which has one and only one positive root on the intervalΛ∈(0,1)according to Descartes’ sign rule.

To further investigate the number of positive roots of the quintic equation as shown in Eq.(21) on the intervalΛ∈(0,1),we need to consider the following critical case in which the stationary point of the pressure–volume curve is exactly located on the volume axis or the lineP0.In such a case,we have

After several times of iteration,Eq.(23) becomes equivalent to the following simple relations:

in which the involved coefficients are defined by

The above relations can be well fitted numerically by the least square method with a constraint conditionΛ0|ξ00 as

Having obtained Eq.(26),we are thus able to determine the number of positive roots of Eq.(21) on the intervalΛ∈(0,1)with the aid of Descartes’ sign rule by additionally noticing that

The final results are presented in Fig.2.

There exist some cases where only the first half of the pressure–volume curve becomes important in the structural design.A practical and important question arises naturally as follows:given the designed values of the initial slopeKinitialthe peak valuePpeakand the corresponding volumeVpeakof the pressure–volume curve,how to determine the desired geometrical and material parameters uniquely? The answer to this question will be given below.

Firstly,the explicit expression ofΛpeakcan be obtained by settingVVpeak in Eq.(18).By substituting such an explicit expression ofΛpeakinto Eqs.(17) and (21),we can easily determine the explicit expressions ofξandC1,respectively,as

Then,by substituting Eqs.(28) and (29) into Eq.(19),respectively,we can find out a nonlinear equation for the unique determination ofΛ0as

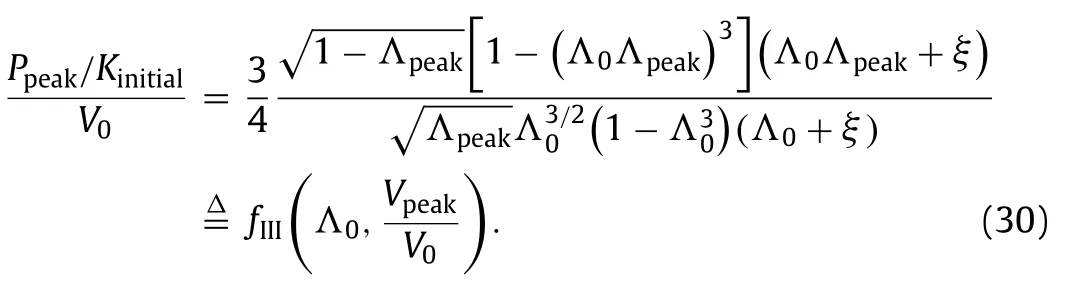
It should be emphasized that Eq.(30) is subjected to an inequality constraint as follows:

which is derived from the fact that the curvature of the pressure–volume curve at the so-called peak point must be negative (or zero).

OnceΛ0is determined from Eq.(30) under the constraint condition of Eq.(31),by resubstitutingΛ0into Eqs.(28) and (29),we can thus get the values ofξandC1,respectively.If only the values of the geometrical and material parameters are located within the admissible region,the quantitative design will complete.We also point out here that,since the Mooney–Rivlin constitutive model is generally suitable for moderate stretching ratios smaller than 200% [29],another constraint condition should also be added,i.e.Λ0Λpeak≥1/220.25.

As an example,suppose that there is an elastomeric circular membrane composed of Mooney–Rivlin solids,having a radius ofR015 mm and a thickness oft00.15 mm in the natural state.Now,we need to select appropriate values of the prestretching ratioλ0and the material parametersC1 andC2,so that the corresponding pressure–volume curve has an expected peak point(Vpeak/V0,Ppeak)(2,2 kPa)and an expected initial slope satisfying(Ppeak/Kinitial)/V04/3,where 7.07 mL.The design process is summarized as follows.Firstly,substitutingVpeak/V02 into Eq.(18),we get an explicit expressionΛpeakΛpeak(Λ0).Secondly,substitutingΛpeakΛpeak(Λ0)into Eq.(28),we get an explicit expressionξξ(Λ0).Thirdly,substitutingΛpeakΛpeak(Λ0),ξξ(Λ0),and(Ppeak/Kinitial)/V04/3 into Eqs.(30) and (31),we get an implicit nonlinear equationfIII(Λ0,2)−4/30 inΛ0subjected to a constraint condition,say,fVI(Λ0)≥0.Solving the above nonlinear equation with constraints numerically,we find thatΛ00.8637,i.e.λ01.076.ResubstitutingΛ00.8637 intoξξ(Λ0),we find thatξ0.0462.SubstitutingΛpeakΛpeak(Λ0),Λ00.8637,ξξ(Λ0),R015 mm,t00.15 mm andPpeak2 kPa into Eq.(29),we find thatC150.305 kPa and furtherC2ξC12.3237 kPa.In addition,the substitution ofΛ00.8637 intoΛpeakΛpeak(Λ0)givesΛpeak0.3579,which satisfies the aforementioned constraint conditionΛ0Λpeak≥0.25.The designed pressure–volume curve as expected is finally shown in Fig.3a.The second half of the pressure–volume curve is also presented as shown in Fig.3b.

Fig.3. The designed pressure–volume curve as expected: a on a small scale; b on a large scale.

To verify the validity of our spherical-cap assumption and analytical solution,we now compare them with numerical results from the conventional finite element method (FEM) via commercial software ABAQUS.The axisymmetric model and the shell element (element type:CAX4RH) are used in the FEM simulation,where the element numbers in the thickness and radial directions are 8 and 1000,respectively.The fixed boundary condition is assigned at the rim and the Risk method is used during the inflation process.The geometrical and material parameters of the models adopted are listed as follows:R015 mm,t00.15 mm,λ01.2(Λ00.6944),C120 kPa,C2ξC1,whereξ0.3 orξ0.05.For the sake of convenience in comparisons,the profile of the inflated membrane will be visualized by its vertical section coplanar with the center of the undeformed circular membrane,and the pressure-height curve (i.e.theP−Hcurve),instead of the pressure–volume curve (i.e.theP−Vcurve),will be investigated by considering the difficulty in extracting the volume data from ABAQUS.The analytical solution for the pressure-height curve are given explicitly as

At one aspect,it can be observed from Fig.4 that the profile of the inflated membrane is reasonably approximated by some spherical cap whenH/R0<1,which validates the spherical-cap assumption to a certain extent.It should be pointed out that the circular arcs in Fig.4 are just plotted by fitting such that each circular arc passes through the apex of the corresponding profile and the two fixed points at the rim.At another aspect,it can be observed from Fig.5 that acceptable agreements for theP−Hcurve are achieved between the FEM data and the analytical solution as shown in Eq.(32) when the height of the inflated membrane is relatively small,i.e.H/R0<1.However,as the height further increases,the deviation of the analytical solution from the FEM data continues to increase.Next,some improvements to the above analytical solution are proposed to reduce such a deviation.The basic idea is demonstrated as follows.

Fig.4. Comparisons between the FEM data and the spherical-cap approximation for profiles of the inflated membrane: a ξ 0.3; b ξ 0.05.

Actually,it makes the membrane structure stiffer to artificially enforce the inflated membrane to be some spherical cap subjected to equi-biaxial stretching.To compensate for the above artificial constraint as reasonably as possible,it becomes a natural way to relax the circumferential constraint from the fixed rim appropriately.To achieve this,referring to Fig.1d,we can calculate the stretching ratio in an alternative way,by considering the uniform stretch of the circular arc on the big circle of the fictitious closed spherical surface,below:

Fig. 5. Comparisons between the FEM data,the analytical solution,and the improved solution for the pressure-height curve: a ξ 0.3; b ξ 0.05.

which leads to

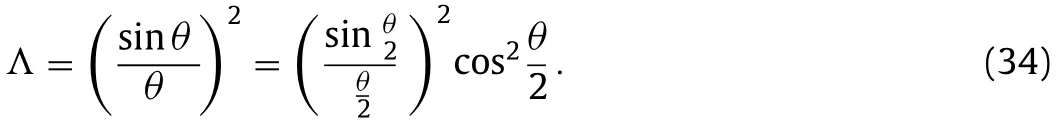
The above calculation indicates that,unlike the way to derive Eq.(10),some material points are permitted to flow into and out of the circular rim of the membrane for the satisfaction of equibiaxial stretching states.We can also see that the only difference between Eqs.(10) and (34) is that a modulation function appears in Eq.(34).When the angleθis quite small,the modulation function is nearly equal to 1 and thus makes little contribution to the improvement.However,as the angleθincreases,the improvement arising from the modulation function becomes more and more significant.In summary,the improved solution can be written as

in whichΛis defined by Eq.(34).

It can be observed from Fig.5 that,the improved solution given by Eqs.(34) and (35) matches the FEM data better than the original analytical solution shown in Eq.(32).Note that,as presented in Fig.5,the FEM simulations based on the Riks method fail to converge due to severe mesh distortions near the rim of the inflated membrane when the stretching ratio becomes large enough.

Correspondingly,the improvedP−Vcurve can be expressed explicitly as

whereΛis a function ofθshown in Eq.(34),andθis given by Eq.(8) as

In summary,we have analytically studied the inflation of a pre-stretched elastomeric circular membrane under uniform pressure.Based on the reasonable assumption that the inflated circular membrane can be approximated by some spherical cap,we have derived an explicit analytical solution for the pressure–volume curve by using the Mooney–Rivlin constitutive model.The dependence of the characteristics of the pressure–volume curve (e.g.the initial slope and the number of stationary points) on the prestretching ratio and the material parameters has been clearly revealed.The analytical solution has been further used to design the desired pressure–volume curve with prescribed peak point and initial slope.Some improvements to the analytical model have also been proposed for a better quantitative prediction.This work would be of practical value to the quantitative design of elastomeric membrane structures in some emerging fields such as soft robotics and flexible electronics.

Contribution

J.Y.supervised this work,derived solutions,conducted analysis and wrote the manuscript;X.L.and H.X.checked solutions;X.L.and Y.H.completed numerical examples;Y.H.modified the manuscript;and all of the co-authors contributed to discussion.

DeclarationofCompetingInterest

We would like to declare that no conflict of interest exists in the submission of this manuscript,and this manuscript is approved by all authors for publication.

We would like to declare that the work described was original research that has not been published previously,and not under consideration for publication elsewhere,in whole or in part.All the authors listed have approved the manuscript that is enclosed.

Acknowledgments

Supports from the National Natural Science Foundation of China (Grants 11772272 and 11972027) are greatly acknowledged.J.Y.also acknowledges the support from the Fundamental Research Funds for the Central Universities (Grants 2682019LK06 and 2682019LXCGKY001).