Effect of interfacial stiffness on the stretchability of metal/elastomer bilayers under in-plane biaxial tension
2021-08-14ZhengJiaTengLi
Zheng Jia ,Teng Li
a Department of Engineering Mechanics, Center for X-Mechanics, Key Laboratory of Soft Machines and Smart Devices of Zhejiang Province, Zhejiang University, Hangzhou 310027, China
b Department of Mechanical Engineering, University of Maryland, College Park 20742, MD, USA
Keywords:Metal/elastomer bilayers Stretchability Interface Necking
ABSTRACT Flexible electronic devices are often subjected to large and repeated deformation,so that their functional components such as metal interconnects need to sustain strains up to tens of percent,which is far beyond the intrinsic deformability of metal materials (~1%).To meet the stringent requirements of flexible electronics,metal/elastomer bilayers,a stretchable structure that consists of a metal film adhered to a stretchable elastomer substrate,have been developed to improve the stretch capability of metal interconnects.Previous studies have predicted that the metal/elastomer bilayers are much more stretchable than freestanding metal films.However,these investigations usually assume perfect bonding between the metal and elastomer layers.In this work,the effect of the metal/elastomer interface with a finite interfacial stiffness on the stretchability of bilayer structures is analyzed.The results show that the assumption of perfect interface (with infinite interfacial stiffness) may lead to an overestimation of the stretchability of bilayer structures.It is also demonstrated that increased adhesion between the metal and elastomer layers can enhance the stretchability of the metal layer.
Flexible electronic devices are being developed for diverse applications,such as epidermal electronics [1],skin-like biosensors[2],stretchable batteries [ 3,4 ],as well as wearable and implantable systems [ 5,6 ].The flexible devices are often subject to large and repeated deformation.Functional components in the devices such as metal interconnects deform with the device and consequently undergo mechanical strains up to a few tens of percent.However,metal materials (e.g.,copper and aluminum) commonly used as interconnects often fracture at a small strain (~1%),via necking instability [ 7,8 ].To this end,limited deformability of metal interconnects is a concern in a broad range of contexts including flexible electronics and stretchable batteries.The need for improving the deformability of metal materials to meet the stringent requirements of flexible electronic devices has induced an impetus to develop flexible structures such as metal/elastomer bilayers that consist of a metal layer adhered to a stretchable elastomer substrate[ 9,10 ].The elastomer substrate may delocalize the strain field in the metal film and delay the formation of necking [11–14],thereby carrying the metal film to a strain level far beyond the fracture strain of a freestanding metal layer.For example,both simulations and theoretical studies have revealed that bonding a metal film to an elastomer substrate may increase its stretchability by several folds [ 11,15,16 ].Experimental evidence has also accumulated that metal films adhered to polymer substrates can sustain strains up to 50% before rupture [17] .In these investigations,perfect interfacial bonding has been assumed between the metal and elastomer layers [ 11,12,15 ].However,localized and inhomogeneous deformation due to necking formation may lead to the loss of adhesion between the two layers [ 18,19 ].Recent experiments have suggested that the stretchability of such a polymer-supported metal film is sensitive to its adhesion to the polymer substrate [ 20,21 ].In this work,we outline a theoretical model to study the influence of interfacial adhesion on the stretchability of metal/elastomer bilayers,by extending the method we developed previously [15] .The effect of imperfect interface with a finite interfacial stiffness on the stretchability is analyzed and the results demonstrate that reduced adhesion between metal and elastomer layers can promote necking instability,undermining the stretch capability of the metal/elastomer bilayers.
We consider a metal/elastomer bilayer structure located in the plane prescribed by axesx2 andx3,as shown in Fig.1 .The bilayer is subjected to an in-plane biaxial proportional loading,with the in-plane strain components given byε2Xcosα,ε3Xsinα.Herein,αis defined as the strain ratio angle since the strain ratioε3/ε2equals to tanα,andXspecifies the in-plane strain amplitude.For proportional straining,αremains fixed whileXincreases monotonically.Assuming both the metal and elastomer layers are incompressible,the out-of-plane strain componentε1can be obtained thatε1−ε2−ε3.Notably,the critical value ofX(denoted asXchereafter) above which the elastomer-supported metal film ruptures by necking formation characterizes the stretchability of the metal/elastomer bilayers.The aim of this work is to evaluate the effect of interfacial stiffness on the value ofXc,i.e.,the stretchability of the bilayer structures,given a strain ratio angleα.
We first present the constitutive relations of the metal layer and elastomer layer,respectively.The material behavior of incompressible and rate-independent metal layer can be described by the finite strain J2 deformation theory of plasticity [8,15,22],with the constitutive law having the form

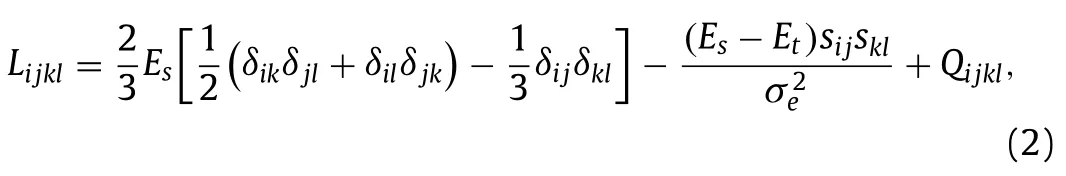
wheresijdenotes the deviatoric stress andis the effective stress,EsandEtare the secant modulus and tangent modulus,respectively.For a metal material characterized by a powerlaw hardening behaviorσKεN(Krepresents the modulus of the metal material andNis the hardening index),the secant modulus and tangent modulus are given byEsand,respectively (εeis the effective strain).Qijklsatisfies the indicial symmetry thatQijklQjiklQijlkQklijand only the following components are non-zero in principal axes.
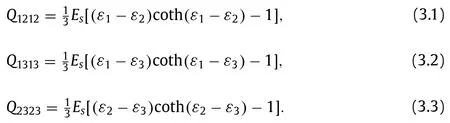
According to the deformation theory of plasticity,the relation between the principal strain and the principal deviatoric stress is given asεiwhereεiandsi(i1,2,3) represent Eulerian strain and deviatoric stress in principal directions,respectively.Take into account the plane-stress conditionσ10,the inplane Cauchy stresses in the metal layer is obtained as
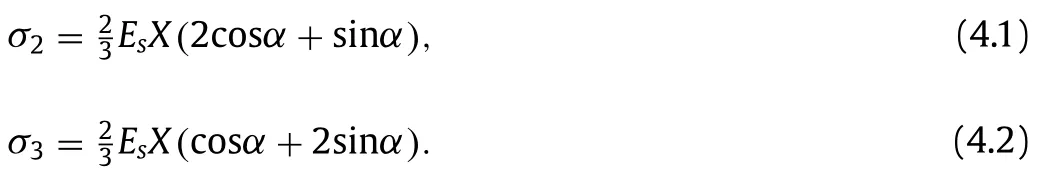
In addition,the effective stress and effective strain are given by
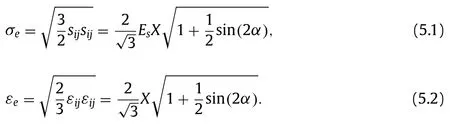
The constitutive law of the elastomer layer is described by the incompressible NeoHookean model,of which the strain energy density isWwhereEis the initial Young’s modulus andthe principal stretch.According to Biot [23],the rate form of constitutive law for a NeoHookean material can be expressed as follows

Moreover,the Cauchy stress components in the elastomer substrate are
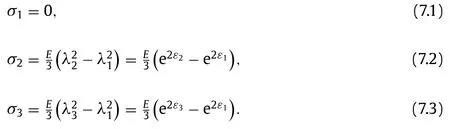
As abovementioned,Xcis corresponding to the onset of necking instability and thus can be numerically solved by performing a bifurcation analysis.We next introduce the procedure of the bifurcation analysis [15].When the metal/elastomer bilayer structure is subjected to a subcritical biaxial loading,both layers deform homogeneously so that the equilibrium equations are trivially satisfied.When the loading increases to a critical level,the necking instability occurs,and a non-trivial solution which represents nonhomogeneous deformation state becomes possible.A perturbation in the velocity fieldvi(i1,2,3),which is associated with the non-homogeneous deformation state,gives rise to a small increment in the asymmetric nominal stress tensortij.The increment of the nominal stress field must satisfy the equilibrium equation,such that

The relation between the Jaumann rate of Cauchy stress and the nominal stress rate is
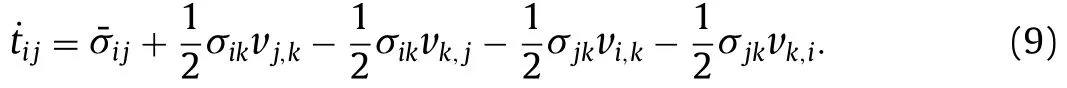
Substituting Eqs.(1) and (9) into Eq.(8) gives that

In addition to Eq.(10.1),the incompressibility condition requires that

Equation (10) constitutes the governing equations for the bifurcation analysis.Notably,the development of these equations does not rely on any prescribed constitutive law so that they are valid for both the metal layer and the elastomer layer.Explicit expressions of coefficientscijklfor both the metal layer and the elastomer layer have been derived by Jia and Li [15].
In both layers,nontrivial solutions to the governing Eq.(10) take the form that

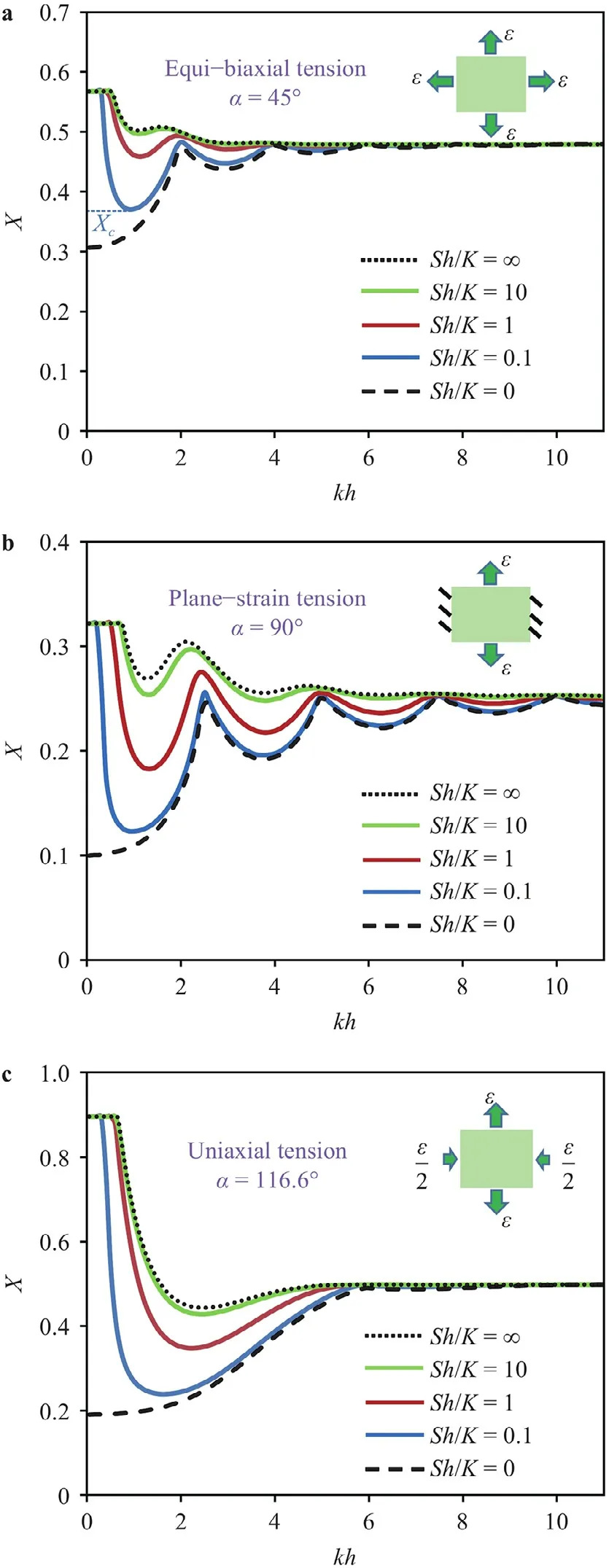
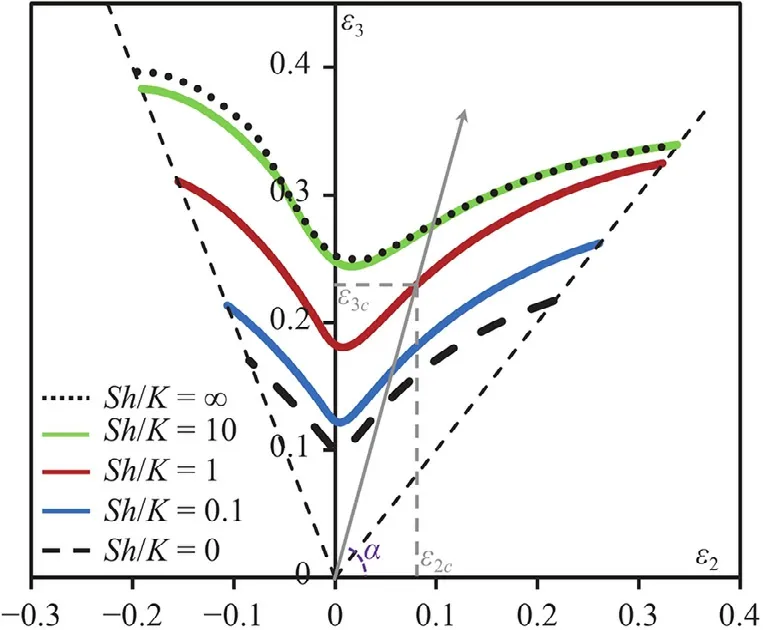
whereAj(j1,2,...,4)andzare parameters which take complex values.k2kcosΩandk3ksinΩare wavenumbers,wherekis a positive number (0 Plugging the solutions given in Eq.(11) into the governing Eq.(10) yields 4 linear algebraic equations forA1,A2,A3andA4, Expressions ofMijhave been derived by Jia and Li [15],which depend onz,X,Ωandk.Necking instability occurs whenAbecomes nontrivial,such that the critical condition for necking requires Equation (13) leads to a cubic equation ofz2,with six complexvalued rootszi(i1,2,...,6).LetAj(i)(j1,2,...,4)be a normalized nontrivial solution to Eq.(12) associated withzi.Then the velocity field specified by Eq.(11) can be expressed as a linear combination ofAj(i)(i1,2,...,6) where Re[] denotes the real part of a complex number.ξi(i1,2,...,6)are six coefficients to be determined by using boundary conditions. Note that Eqs.(8)–(14) are applicable for both the metal layer and the elastomer layer,but the values ofzi,Aj(i),andξi,in general,differ between the metal layer and the elastomer layer.To this end,in the following we use the superscripts+and −to denote quantities in the metal film and elastomer substrate,respectively,as highlighted in Fig.1.For example,,andare for the metal layer,and,andare for the elastomer substrate.Notably,there are twelve boundary conditions for the bilayer structure:At the top surface of the metal film,three traction rates vanish;At the bottom surface of the elastomer substrate,three traction rates vanish;At the film/substrate interface,three traction rates are continuous and the velocity jump across the interface is related to the traction rates by an interfacial traction-separation law (Fig.1), The 3 × 3 matrix above,also denoted asS,characterizes the stiffness of the interfacial adhesion between metal and elastomer layers.In two limiting cases,S→∞corresponds to the perfectly bonded interface that does not separate at all (i.e.,the velocity field is continuous across the interface);andS0corresponds to the fully detached interface (i.e.,the metal film is freestanding without any support from the elastomer substrate). The abovementioned boundary conditions give a set of 12 linear algebraic equations for unknownswith a 12 × 12 coefficient matrixH.Hence the onset of necking instability requires For a given proportional straining history withαbeing fixed,Eq.(17) together with Eq.(13) determines the criticalXthat triggers the necking instability for a given combination ofkandΩ.Stretchability (i.e.,Xc) of a metal/elastomer bilayer is set by the lowest criticalXfor 0 In the following,we present results of bifurcation analysis of the metal/elastomer bilayers.We assume that the interfacial stiffness tensorSis isotropic,i.e.,S11S22S33S.The bilayer system is characterized by four dimensionless parameters:hardening indexN,thickness ratioH/h,modulus ratioE/K,and normalized interfacial stiffnessSh/K.In this study,the following values are used:N0.1,E/K1.05,H/h5.We vary the value of normalized interfacial stiffness to elucidate the effect of interfacial stiffness on the stretchability of the metal/elastomer bilayers. Figure 2 presents how the stretchability of the bilayer structure is determined for a given strain ratio angleα.We choose three representative loading conditions:(i)α45◦(ε2/ε31) for equibiaxial tension (Fig.2a),(ii)α90◦(ε2/ε30) for planestrain tension (Fig.2b),and (iii)α116.6◦(ε2/ε3−0.5) for uniaxial tension along thex3 direction (Fig.2c).In Fig.2,for each representative loading condition,the critical value ofXthat triggers the necking instability of a given dimensionless wavenumberkhis plotted.For anykh,the criticalXis obtained by finding theΩthat minimizes the value of criticalX.The lowestXon each curve,i.e.,Xc,determines the stretchability of the metal/elastomer bilayer under the biaxial loading (as highlighted in Fig.2a).In two limiting cases,the curves ofSh/K∞andSh/K0 correspond to a bilayer with a perfectly-bonded interface and freestanding metal film completely detached from the substrate,respectively.Comparison between the two limiting cases clearly reveals that well adhering a metal film to an elastomer substrate can significantly increase the stretchability of the structure:for example,whenα90◦(Fig.2b),Xcis 0.1 for the free-standing metal film and close to 0.25 for the metal/elastomer bilayer with a perfectly-bonded interface.It is also evident in Fig.2 that theX-curves associated with a finite interfacial stiffness lie between the two limiting cases:the smaller the value ofSh/K,the weaker the interface,and the lower the stretchability of the metal/elastomer bilayer. Fig. 2. Critical value X at which necking instability occurs is plotted as a function of dimensionless wavenumber kh,for three representative proportional straining cases:a α 45◦,b α 90◦,and c α 116.6◦.Note that the lowest point on each curve gives the stretchability of the metal/elastomer bilayer X c . Fig. 3. Stretchability curves of metal/elastomer bilayer structures with various interfacial stiffness values. Figure 3 plots the stretchability (in terms ofε2andε3) of the bilayer structures with various normalized interfacial stiffnessSh/K.In the plot,proportional loading of a givenαcorresponds to a radial line that makes an angleαwith the axis ofε2(depicted in Fig.3 as the solid arrow line),on whichε2Xcosαandε3Xsinα.The range ofαthat we investigated is from 45◦(equibiaxial tension) to 116.6◦(uniaxial tension).The intersection point of the radial line and the stretchability curves gives the critical strains (ε2cXccosαandε3cXcsinα) that trigger the necking instability.Figure 3 demonstrates the significance of the interface stiffness in determining the stretchability of the metal/elastomer bilayer:the metal/elastomer bilayer structure of a stiffer interface possesses a higher stretchability.It is also noteworthy that the laminate of a sufficiently strong interface (Sh/K10) already has a comparable stretchability to a metal film perfectly bonded to the underlying elastomer substrate. In summary,we investigate the influence of the imperfect interface on the stretchability of metal/elastomer bilayer structures– which have been widely employed as interconnects and electrodes in flexible electronics.We show that the stretchability of metal/elastomer bilayer structures with an interface of finite interfacial stiffness is higher than a freestanding metal film but lower than a metal film perfectly bonded to an elastomer substrate.That is,previous studies assuming perfect interfacial bonding (with infinite interfacial stiffness) may overestimate the stretchability of the metal/elastomer bilayers,considering that the interface in reality can hardly be perfectly-bonded.It is also revealed that the higher the interfacial stiffness is,the more stretchable the metal/elastomer bilayers are.Emerging from the above findings is a structural design strategy to enhance the stretchability of metal films,that is,by adhering a metal layer onto the surface of an elastomer substrate via a strong interface. DeclarationofCompetingInterest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.



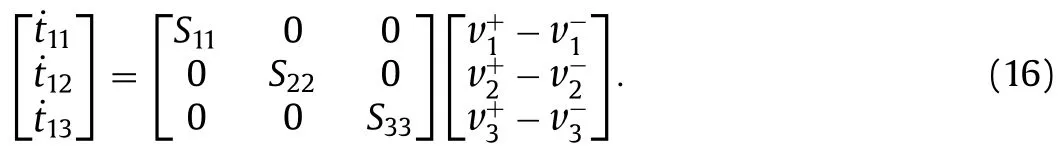

杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- A geometry-based framework for modeling the complexity of origami folding
- Why neural networks apply to scientific computing?
- Analytical solutions for inflation of pre-stretched elastomeric circular membranes under uniform pressure
- Computing mean fields with known Reynolds stresses at steady state
- Fundamental kinematics laws of interstitial fluid flows on vascular walls
- Analytical and numerical studies for seiches in a closed basin with various geometric shapes of longitudinal section
