基于MATLAB的多连杆机械人动力学方程建立
2021-08-13冯小庭王航
冯小庭,王航
(西安铁路职业技术学院,陕西 西安 710026)
0 引言
机器人广泛应用于医疗器械、汽车工业、建筑工程以及石油工业。工业机器人是一个复杂的动力学系统,它由多个关节和多个连杆组成,具有多个输入和多个输出,连杆之间存在着非线性耦合关系。研究机器人动力学是为了实现高精度的实时控制,以完成高质量的生产过程。因此,是否可以准确高效地获得机器人的动力学方程是非常必要的。而在一些领域对平面多连杆机器人有着特殊需求。平面连杆机器人连杆数量的增加可以提高使用的灵活性。当连杆的数量增加时,机器人的动力学建模将是非常繁琐的过程。众多文献对机器人连杆或通过函数求解运动方程,或三维软件建模以及获得动力学方程,但是随着连杆数量的增加,求解耗时多,且容易出错;运动仿真的精度有待验证。
本文使用MATLAB使得多连杆机器人的动力学建模得到简化,可以实现任意多连杆平面机器人的建模。以七连杆机器人的建模过程验证本程序的正确性。本程序亦可用于关节有驱动力时,连杆机器人末端轨迹的仿真。
1 多连杆机器人的建模
本文使用拉格朗日法对连杆机器人进行动力学建模。为了获得各连杆的位置,需要首先知道D-H附体坐标系的矩阵表示方法。
连杆的变换矩阵为:
(1)
其中i=1,2,…,n。
式中:αi为连杆扭转角;ai为连杆长度;di为连杆偏移量;θi为关节转角。
由式(1)可以知道任意连杆相对于基础坐标的位置。
连杆机器人简图如图1所示。有n个连杆的机器人有n个自由度,每个连杆有1个自由度。机器人动力学方程的一般公式表示如下。
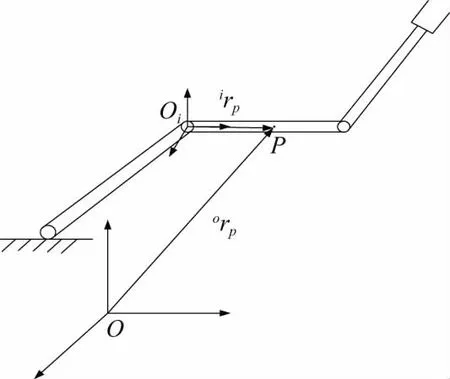
图1 连杆机器人简图

(2)

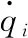
(3)
(4)
在编写相关的程序时,直接引用了上述的推导结果。上式中,第一部分是角加速度惯量项,第二部分是驱动器惯量项,第三部分是科里奥利力和向心力,最后是重力项。惯量项和重力项对于机器人系统的稳定性和定位精度至关重要。向心力和科力奥利力在机器人低速运动时可以忽略,但在机器人高速运动时,其作用非常重要。
2 动力学建模
2.1 七连杆机器人的动力学模型

(5)
其中i=1,2,…,n。
由于,本文针对的是平面连杆机器人,故式(1)中αi=0,di=0,变换矩阵写为
(6)
第i的伪惯量矩阵为:
(7)
式中:INi是第i个连杆相对于坐标系Oxiyizi的转动惯量。这里假设机器人的连杆是均匀的细直杆,则
(8)
一般连杆机器人的动力学公式写为如下的矩阵形式[9]:

(9)

七连杆机器人的动力学公式可以写为下式:
(10)
2.2 程序设计
在这里需要做出补充说明,本文的连杆机器人动力学建模程序只针对基座固定的机器人而言。而且本程序目前只适用于平面串联圆柱关节机器人。
MATLAB强大的符号工具箱是本文所述内容得以实现的根本原因。程序的编写主要参照了上述连杆机器人普遍动力学公式的推导过程。下文将会围绕程序的核心部分进行说明。程序中较多的使用元胞数组,这是MATLAB特有的数据结构。得益于计算机技术的提升,这种数据结构使得计算的过程简化,代码的逻辑易读,尽管元胞数组会额外增加计算机内存的使用。
在系统动力学的推导过程中,并没有考虑关节处的驱动机构的转动惯量,且没有考虑关节处的摩擦力。当然,程序中添加计算驱动装置的转动惯量和摩擦力是非常易于实现的。其次,计算出的动力学公式,仅需极小的改动即可应用于其他语言的仿真程序中。例如可以直接将计算结果粘贴到C语言中,进行运动的仿真。
主程序调用的子函数中最重要的输入变量是连杆之间的附体坐标变换矩阵。为了简化程序的实现过程,将连杆变换矩阵存储在元胞数组中。本计算方法的实现完全依照式(3)、式(4),难点在于附体坐标系相对于基坐标系的变换矩阵以及中间变换矩阵的获得。设需要建立的机器人的连杆数是num,预先建立num+1阶的元胞数组T。元胞数组T{i,i}储存的是单位矩阵,T{i,i+1}储存的是第i个连杆的变换矩阵。为获得坐标系之间的变换矩阵,引入如下的算法。限于篇幅,这里只摘录部分关键代码。
for ii=1:num+1
for jj=1:num+1
if((ii+1)==jj)||(ii>=jj)
continue;
else
T_temp=sym(eye(4));
n_temp=jj-ii;
for kk=1:n_temp
T_temp=T_temp*T{ii+kk-1,ii+kk};
end
T{ii,jj}=T_temp;
end
end
end
其中的元胞数组T即是所求,后续的计算过程主要围绕该数组的读取及应用。
2.3 动力学方程
通过调用相关的程序,即可得出相关的结果。由于系数矩阵的结构非常复杂,限于篇幅,只将其中的一部分摘录如下:
m5a2a4cos(q3+q4)+m6a2a4cos(q3+q4)+m7a2a4cos(q3+q4)+
m6a4a6cos(q5+q6)+2m7a4a6cos(q5+q6)+m7a5a7cos(q5+q6)+
m5a2a4cos(q3+q4)+m6a2a4cos(q3+q4)+m7a2a4cos(q3+q4)+
m7a3a4cos(q4)+m5a4a5cos(q5)+2m6a4a5cos(q5)+
2m7a4a5cos(q5)+m6a5a6cos(q6)+2m7a5a6cos(q6)+
m7a3a4cos(q4)+m5a4a5cos(q5)+2m6a4a5cos(q5)+
m7a3a6cos(q4+q5+q6)+m7a4a7cos(q5+q6+q7);
m6a4a5cos(q5)+m7a4a5cos(q5)+m6a5a6cos(q6)+2m7a5a6cos(q6)+m7a6a7cos(q7)+
由以上公式可知,七连杆机器人的动力学公式是极其复杂的非线性公式。
3 数值仿真
动力学仿真主要用于验证计算方法的正确性,若动力学模型有误,则仿真结果也将产生误差,一般而言会使计算的结果发散。以2.1节中七连杆机器人为例,在各关节处施加正弦力矩信号,得到了七连杆机器人的运动轨迹图,如图2-图3所示(本刊黑白印刷,相关疑问咨询作者)。为了使从动力学模型到仿真的计算过程更加便利,本文依然借助于MATLAB来实现建模和仿真的无缝衔接。具体而言,就是将得到的符号函数转换为函数句柄,这个过程是通过MATLAB自带的函数完成的,即使用MATLAB Function(symstring)函数,其中函数的输入为symstring是符号函数表达式。这样做会增加仿真过程的耗时,但是考虑到计算的总时长较短,而且这种方法不会发生誊录公式时易发生的错误。常微分方程组的数值解使用的是定步长四阶龙格库塔法。设机器人各连杆的长度都为1.0 m,质量为2 kg,各关节处的转矩幅值均为20 N·m。计算的步长为0.001 s,仿真的时间为1s。

图2 角位移

图3 角速度
由于七连杆机器人的动力学模型非常复杂,因此仿真的时间较短。从图2、图3中可以看出,七连杆机器人的角位移、角速度的变化均较为剧烈,但都呈现出连续的曲线形式。图4是机器人是动作姿态。在整个时间历程中,等时间间隔地选取其中5个时间节点的动作姿态。可知末端连杆的位形改变得较大,机器人整体呈现竖直的趋势,这是因为关节力矩不足以抵消重力的影响所导致的,因而整体有向下运动的趋势。

图4 连杆的动作姿态
4 结语
由七连杆机器人的动力学仿真可知,在2连杆、3连杆情况下推导出的结果与一般方法的动力学方程完全一致,可知在多连杆的情况下本方法也是正确的。本方法未考虑连杆之间的内力,简化了推导的过程,提高了推导的效率和正确性。本方法对后续、复杂的、有平移关节和球关节组成的空间型机器人的动力学推导有一定的借鉴意义;也对平面开链多连杆柔性机器人的动力学建模有借鉴意义。
