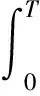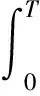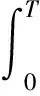一类部分可观测的倒向重随机控制系统
2021-08-13王维峰郭仲凯
王维峰,郭仲凯
(中南民族大学 数学与统计学学院,武汉430074)
最优控制问题普遍存在于自然科学和社会生活的各个领域,它主要是对一个动力系统寻求最优的控制策略,使某个目标量达到最大或最小. 随机控制理论将随机过程理论与最优控制理论相结合,成为研究随机系统的一种有效方法,被广泛应用到物理学、经济学、工程学、生物学等学科中. 1994年,PARDOUX 和PENG首次研究了倒向重随机微分方程,给出了方程解的存在唯一性[1]. 2006年,SHI 和 WU在非凸控制区域情形下研究了耦合正-倒向随机控制系统的最大值原理[2]. 2010年,HAN等研究了倒向重随机控制系统的最优控制问题,在凸控制区域情形下得到了上述问题的最大值原理[3].
上述研究中,控制系统都是完全可观测的. 但是,在很多情形下对系统进行控制的时候,仅仅只能观察到部分信息. 比如,在金融数学中的最优投资组合选择问题中,投资者仅仅只能获得证券股票以前以及当前的价格(动态),不可能了解所有的价格及政策动向,所以投资者只能在所获得的部分信息下进行投资决策. 又比如基金公司的风险控制,他们也只能在获得的有限信息下做出决策,为公司规避风险. 因此,研究只具有部分信息的控制系统很有必要. 到目前为止,对这类问题的研究取得了部分结果. 如TANG研究了一类正向部分可观测系统的最大值原理[4],文献[5-6]研究了正-倒向部分可观测系统的最大值原理,文献[7]在凸控制区域情形下研究了一类部分可观测的倒向重随机控制系统的最大值原理,文献[8-9]在非凸控制区域情形下研究了随机控制系统的一阶和二阶必要条件. 受上述文献的启发,本文对非凸控制区域情形下的部分可观测的倒向重随机控制系统进行了研究和探讨,且控制变量包含在漂移系数和扩散系数中.
1 控制系统的建立
设(Ω,F,P)是完备的概率空间,T>0是一个固定的常数.{W(t):0≤t≤T},{B(t):0≤t≤T}和{Y(t):0≤t≤T}是定义在概率空间(Ω,F,P)上的3个互相独立的标准Brown运动,且分别取值于Rm,Rd和Rr.令N表示F的所有P-零集合.对∀t∈[0,T],给出如下定义:
且:
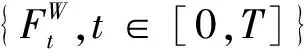


本文需要用到以下推广的伊藤公式[1].
引理1设α∈S2([0,T];Rk),β∈M2([0,T];Rk),γ∈M2([0,T];Rk×d),δ∈M2([0,T];Rk×m)满足:

则有:


更一般地,若Φ(·)∈C2(Rk),则:


令U是Rk中的非空子集,且容许控制集为:
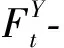
考虑如下的倒向重随机控制系统:

(1)
其中η∈L2(Ω,FT,P,Rn).
假设状态过程(y(t),z(t))不能完全被直接观测,仅能观测到和状态过程相关的一个噪声过程:
(2)

假设以下条件成立:
(H1):(i)函数f:[0,T]×Rn×Rn×m×Rk→Rn,g:[0,T]×Rn×Rn×m×Rk→Rn×d,h:[0,T]×Rn×Rn×m×Rk→Rr关于y、z都是连续可微的;
(ii)fy,fz,gy,gz,h,hy,hz都是有界的.
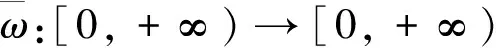
∀t∈[0,T],(y1,z1,u1),(y2,z2,u2)∈Rn×Rn×m×Rk,有:
‖g(t,y1,z1,u1)-g(t,y2,z2,u2)‖2≤
|h(t,y1,z1,u1)-h(t,y2,z2,u2)|2≤
任意给定一个u(·)∈Uad[0,T],由文献[1]中的定理1.1可知,存在唯一解:
(y(·),z(·))=(y(·,u(·)),z(·,u(·)))∈S2([0,T];Rn)×M2([0,T];Rn×d),
满足方程(1).
可以看到方程中有两个独立的布朗运动W(t)和B(t),且其中dW积分项是一个正向的伊藤积分,而dB积分项是一个倒向的伊藤积分.

容易验证Zu(t)∈R是如下随机微分方程的解:
(3)
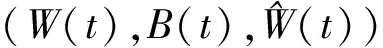
给定如下的目标函数:
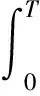
(4)
其中Eu是定义在概率空间(Ω,F,Pu)上的数学期望.
假定如下条件成立:
(H3):(i)函数l:[0,T]×Rn×Rn×m×Rk→R和Φ:Rn→R关于y、z都是连续可微的;
(ii) |ly|+|lz|≤c(1+|y|+|z|),|Φy|≤c(1+|y|).
现在构建最优控制问题(P):寻找一个控制u*(·)∈Uad[0,T]使得:
(5)
任意满足上述等式的u*(·)∈Uad[0,T]都称为一个最优控制,对应的(y*(·),z*(·))称为最优轨道,(y*(·),z*(·),u*(·))称为一个最优序对.
由上可知,目标函数(4)可重述为:
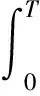
Φ(yu(0))}.
(6)
所以原始的最优控制问题(P)等价于在方程(1)和(3)的条件下最小化(6)式.
2 相关状态变量的估计
假设(y*(·),z*(·),u*(·))是上述最优控制问题的一个最优解.由于控制区域非凸,所以引入如下的针状变分,对任意的u(·)∈Uad[0,T]和0<ε 其中Eε∈[0,T]是一个可测集合且满足|Eε|=ε(ε>0是任意小的).设(yε(·),zε(·))是对应于扰动控制uε(t)的状态轨道. 为了方便,引入如下记号: φ*(·)=φ(·,y*(·),z*(·),u*(·)), 其中φ可以表示文中的函数f,g,l,h,fy,fz,gy,gz,ly,lz,hy,hz. 定理1令ξε(t)=yε(t)-y*(t),ηε(t)=zε(t)-z*(t),则: 证明由状态方程(1)可得: z*(s)]dW(s). 由引理1可知: u*(s))‖2ds. 由条件(H1),(H2)和 Young 不等式,且注意到ξε(T)=0,可得: f(u(s))||ξε(s)|]ds+ 由条件(H2)和0<σ<1,可以选择足够大的M>0使得: 其中λ>0.再由Gronwall不等式,可以得到上述结果. 定理2设Zε(t)和Z*(t)是方程(3)分别对应于控制变量uε(t)和u*(t)的解,则下式成立: E|Zε(t)-Z*(t)|2≤Cε. 证明由方程(3)可知: 对|Zε(t)-Z*(t)|2应用伊藤公式,再结合条件(H2), (H3)和定理1可得: E|Zε(t)-Z*(t)|2≤ h(s,y*(s),z*(s),u*(s))|2+|Zε(t)- Z*(s)|2|h(s,y*(s),z*(s),u*(s))|2]ds+Cε≤ 再由Gronwall不等式,显然有E|Zε(t)-Z*(t)|2≤Cε成立. 下面引入如下的变分方程: (7) 和 (8) 由上述条件可知方程(7)和方程(8)分别存在唯一的适定解(x(t),r(t))∈M2([0,T);Rn)×M2([0,T];Rn×m)和Z1(t)∈M2([0,T];R),0≤t≤T. 定理3设(x(t),r(t))和Z1(t)分别是方程(7)和(8)的解,则: 用类似定理1和定理2的方法证明. 定理4设条件(H1)~(H3)成立,则: 证明由状态方程(1)和变分方程(7)可知: 由引理1,对|yε(t)-y*(t)-x(t)|2用推广的伊藤公式,有: y*(s),z*(s),u*(s))-fyx(s)-fzr(s)-(f(uε(s))- f(u*(s)))](yε(t)-y*(t)-x(t))ds+ u*(s))-gyx(s)-gzr(s)-(g(uε(s))- g(u*(s)))]‖2ds. 由条件(H1)~(H3)和定理1、定理3,化简得: Cε2, 其中λ>0.再由Gronwall不等式知上述前两个不等式成立.用同样的方法可证明第3个不等式. 前面给出了状态方程、变分方程和相关估计量的计算,最后研究变分不等式. 由于假设u*(·)是一个最优控制,因此对任意的扰动控制uε(·)有J(uε(·))≥J(u*(·))成立, 因此: 进而: E(Φ(yε(0))-Φ(y*(0)+x(0)))+ E(Φ(y*(0)+x(0))-Φ(y*(0))). 由条件(H3)、定理1~定理4可得: l(uε(t))-l(u*(t)))]dt+E[Φy(y*(0))x(0)]+Cε. 由上式知,此时变分不等式仅仅是ε的同阶无穷小,而要进一步求出最大值原理,必须要得到变分不等式是ε的高阶无穷小.由此可知,在随机系统下,求得非凸控制区域下的最大值原理将变得非常困难.而为了得到更进一步的结论,通常会将目标函数进行二阶泰勒展开,并将状态方程进行二阶变分,将相关变量进行四阶估计.而此时又需要构造二阶变分方程和二阶伴随方程,这是一个非常复杂的过程,将在后面的工作中进一步研究.
φε(·)=φ(·,yε(·),zε(·),uε(·)),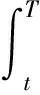
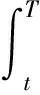
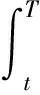
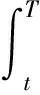

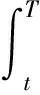




3 变分方程及相关变量的估计
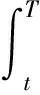
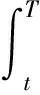
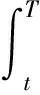
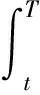
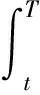
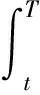
4 变分不等式的探讨