带有吸引Hardy项的临界椭圆方程组解的渐近同步
2021-08-13康东升吴慧敏曹玉平
康东升,吴慧敏, 曹玉平
(1 中南民族大学 数学与统计学学院,武汉 430074; 2 中南民族大学 图书馆,武汉 430074)
1 相关知识
本文主要研究下列方程组:
(1)
其中Δp·:=div(|·|p-2·)是p-Laplacian算子,D1,p(RN)为关于范数的完备化空间,是临界Sobolev指数,并且参数满足下列条件:

g(τ):=λaτp+(μ1-μ2)τa-λb,τ≥0.
一般地,总是假设A<Λ0,Λ0是下面函数的最小正零点:
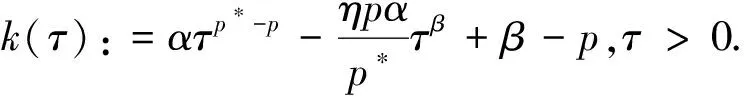

与Hardy不等式[2]相关的临界椭圆方程(组)已经被一些数学工作者研究过(参见文献[3-8]).文献[9]和[10]研究了一类拟线性奇异临界椭圆方程解的渐近性质.但是方程组(1)在λ>0的情形很少被研究(文献[6]初步研究了方程组(1)在p=2时的情形).本文主要研究方程组(1)的径向对称严格递减解在原点和无穷远处的渐近性质,采用的是常微分方程中的分析方法.本文的主要结果如下:
定理1假设条件(H) 成立且A<Λ0,k(A)<0.设(u,v)是方程组(1) 关于原点径向对称和关于|x|严格递减的解.令r=|x|,x∈RN{0},则存在常数C1,C2>0,使得:
2 主要结果的证明
对∀x∈RN,令r=|x|,设(u(r),v(r))是方程组(1)的径向递减解.令L(u):=(rN-1·
|u′(r)|p-2u′(r))′,则有(参见文献[1,11]):
(2)
由此可知rN-1|u′(r)|p-2u′(r)和rN-1|v′(r)|p-2v′(r)是递减的.因为u′(r),v′(r)≤0,那么在(0,+∞)上,有u′(r),v′(r)<0.令:
(3)
于是有yi(t)>0,zi(t)<0,t∈R,i=1,3.结合(2)、(3) 式可得:
(4)
正如文献[6]的讨论,有:
(5)
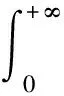
li:=sup{l|gi(l)<+∞}=inf{l|gi(l)>-∞},i=1,2.
同理可以定义:

lj:=inf{l|gj(l)<+∞}=sup{l|gj(l)>-∞},j=3,4,
则有l1=l2,l3=l4,并且
(6)
类似于文献[6]和[7]的讨论,可以得到下列引理,为简单起见省略证明过程.
引理1假设条件(H) 成立,(u,v)>0是方程组(1)的径向递减解.令r=|x|,x∈RN{0},则:
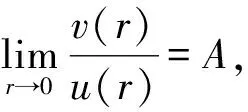
(2) 假设A<Λ0,则:
并且上述上确界和下确界值均无法达到.
引理2假设(H) 成立,A<Λ0,则l1=l2=b(μ*),l3=l4=a(μ*).
引理3假设(H) 成立,A<Λ0,k(A)<0,则ra(μ*)u(r)和rb(μ*)u(r)在(0,+∞)有界.

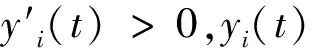

Fρ(H2)=Fρ(H2)-Fρ(a(ρ))=Q(t)(H2-a(ρ)),
(7)
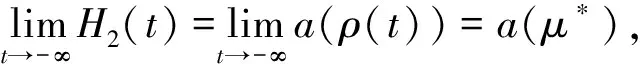
(8)
定义:


(9)
由(4) 和(5) 式,得:
(10)
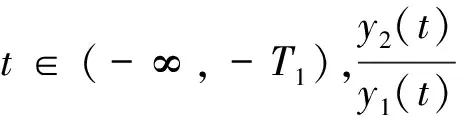
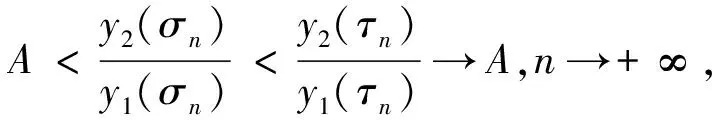
从而f′(A)=Ap-β-1k(A)<0.又因为y1,y2在(-∞,0)上递增,f在A附近递减,g在(0,+∞)递增,a≤α,b≤β,则可以得到:
矛盾.故假设不成立,从而可知命题A成立.为简单起见,可以假设T1=T0,于是有ρ(t)、a(ρ(t))在(-∞,-T0)上递减.
命题B 积分I1,I2有相同的收敛性.
事实上,如果H2(t)在(-∞,-T0)上递增,则:
a(ρ(t)) (11) H2(t)-a(ρ(t))>0, 从(6)~(9) 式可知I1,I2有相同的收敛性,从而命题B成立. 通过计算有: (12) 令ε→0+就有(p*-p)(δ-a(μ*)-ε)>0,再由引理2可以得到: 结合(10) 和(12) 式可得积分I2收敛.由(7)~(9) 式可得积分I1也收敛,又因为: 所以下面的极限存在: 由引理1推出: 则有: 且ra(μ*)u(r)在(0,e-T0)有界.又由引理1可知(ra(μ*)u(r))′<0,所以ra(μ*)u(r)在(0,+∞)上严格递减,从而ra(μ*)u(r)在(0,+∞)有界.同理,函数rb(μ*)u(r)在(0,+∞)也有界. 定理1的证明由引理1和引理3可知函数ra(μ*)u(r)在(0,+∞)严格递减且有界,函数rb(μ*)u(r)在(0,+∞)严格递增且有界,因此下列极限都存在: (13) 其他结果可以从(4) 、(13) 式和引理1直接得出.定理1证毕.

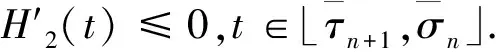
Fρ(H2)<0,∀t∈(-∞,-T0),