空间RSSR机构的装配偏差区间分析

徐旭松，刘 梦，孙志英

(1.江苏理工学院 机械工程学院，江苏 常州 213001；2.浙江省先进制造技术重点实验室，浙江 杭州 310027)

0 引言

空间四连杆机构存在尺寸偏差和运动副间隙，影响机构的运动执行精度，因此在设计阶段需要对各个构件进行尺寸与公差规范，并进行偏差分析。偏差分析应先对尺寸和间隙的变动进行数学建模，然后采用适当的偏差分析方法进行分析。余跃庆等[1]通过优化驱动杆的关节角位移参数来补偿运动副间隙误差，采用全微分法建立了平面3-RRR并联机构的运动模型，并用粒子群算法优化驱动杆的关节角位移参数;赵刘见[2]提出一种考虑柔性和间隙的并联机构动力学与误差分析方法;PAPEGAY等[3]采用符号计算和区间分析法对汽车悬架机构进行了精确运动分析;周勇等[4]采用图解与三维运动仿真相结合的方法对某型空间RSSR机构的几何参数进行了运动分析;赵东平等[5]提出一种基于间隙连接件和多维矢量环的机构装配精度预测方法;牛克佳[6]采用全微分法并考虑运动副间隙来研究平面与空间并联机构误差分析问题;张雷等[7]在考虑制造误差、磨损或装配间隙的情况下，以概率分析方法和非连续接触理论为基础建立了空间引纬四连杆机构的运动学模型，分析了机构的尺寸误差和间隙对整个机构运动输出的影响;WU等[8]采用区间分析法对平面四连杆的杆长和间隙进行偏差建模与分析;CELAYA等[9]提出一种针对平面单环机构的变量区间传播算法，对平面连杆机构位置精度进行了分析研究;MAZZOTTI等[10]将设计参数设定为给定范围内的区间变量，研究空间RSSR机构的尺寸综合设计问题，以力传递的优化为目标函数，将问题设为约束极小化问题，并采用遗传算法和拟牛顿算法进行优化。

文献[1-7,9-10]将机构中的尺寸偏差(或误差)和间隙作为随机变量进行偏差分析与优化，但均未考虑运动副间隙引起的角度偏差。文献[8]以平面四连杆机构为研究对象，采用区间分析法研究了考虑运动副间隙的偏差分析问题。在机构偏差分析实践中，技术人员无法确切知晓尺寸链中各环的概率分布，而采用区间偏差分析求解尺寸链克服了需事先明确各环概率分布的缺陷，具有一定优势。本文在已有研究的基础上，以空间RSSR机构为对象，采用区间分析法研究了杆件尺寸偏差、运动副间隙变动对机构运动角位移的影响，为空间机构的偏差分析研究提供参考。

1 尺寸的区间数表示

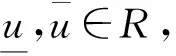
定义2[11]若T=(ξ,η,ζ)，其中0≤ξ≤η≤ζ，称T为一个三角模糊数，隶属函数为：

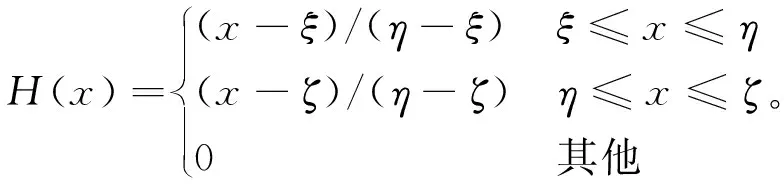
(1)

式中：H(x)∈[0,1]，为x对H的隶属度；ξ,ζ分别为三角模糊数的下确值与上确值;η为三角模糊数最可能的取值。

区间数与模糊数之间具有紧密联系[8]。工程中出现的不确定参数常以一个区间数的形式表示，而三角模糊数则可以描述不确定性的变化，用隶属度来反应区间的变化情况。本文所涉及的三角模糊数属于一型模糊集合，且区间数是模糊数的特例：

(1)对于一模糊数A=[a,b,c]，当a=b或b=c时，模糊数A可表示为A=[a,c]，其中a、c分别表示区间数A的下确值和上确值，且a≤c,a,c∈R，R为实数域。

(2)如图1所示，当隶属函数H(x)为一定值λ时，模糊数A=[a,b,c]可理解为Aλ=[aλ,cλ]。其中：aλ=a+(b-a)λ，cλ=c-(c-b)λ，则有Aλ=[a+(b-a)λ,c-(c-b)λ]，从而将三角模糊数转化为区间数，同时控制区间范围的变化。

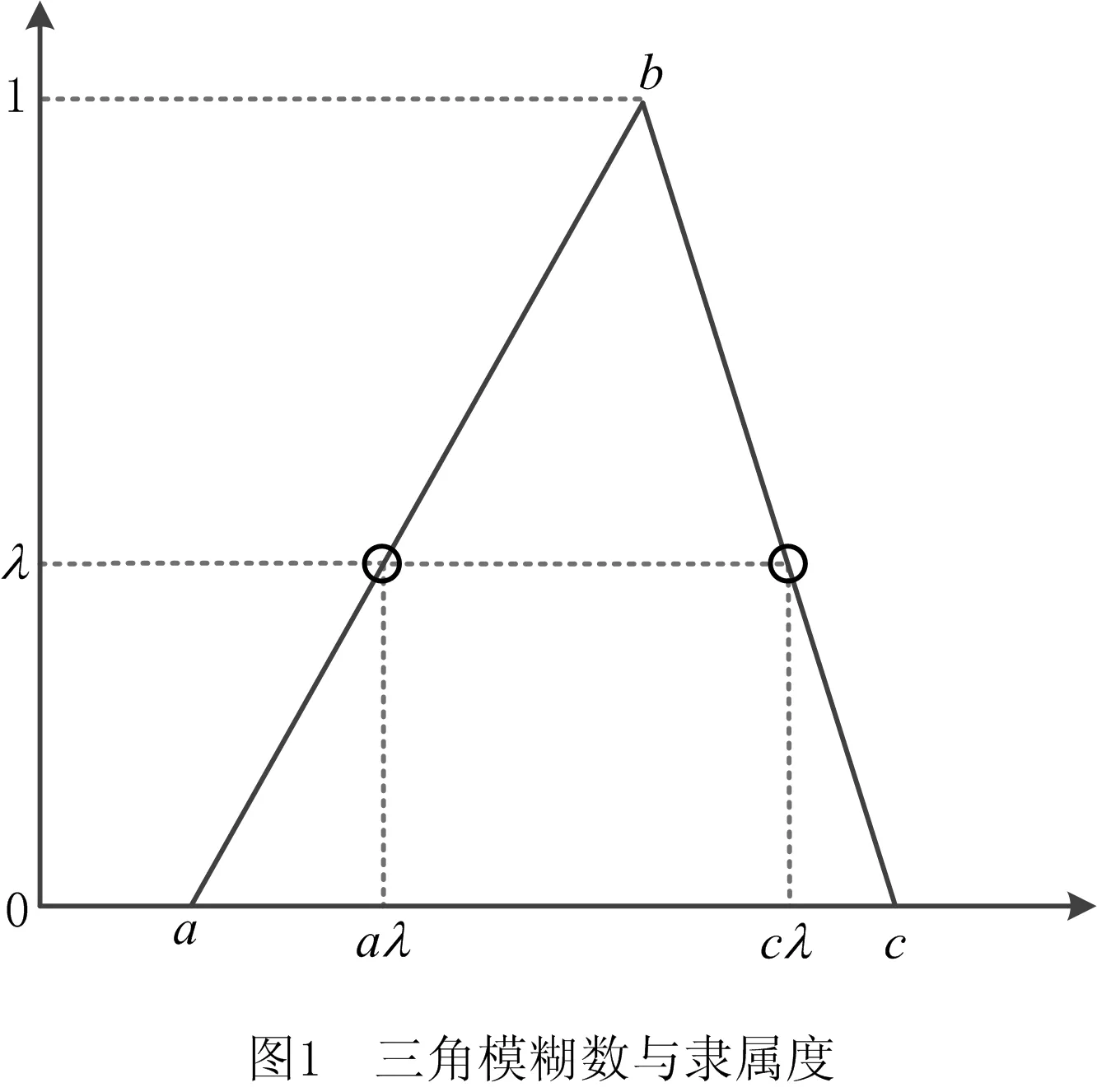
文献[12]对于区间数的基本运算给出了较详细说明。尺寸链中的各环包括线性尺寸、角度尺寸等，其变动范围均可以用区间数的形式进行表示。

2 运动副间隙和杆长偏差区间模型

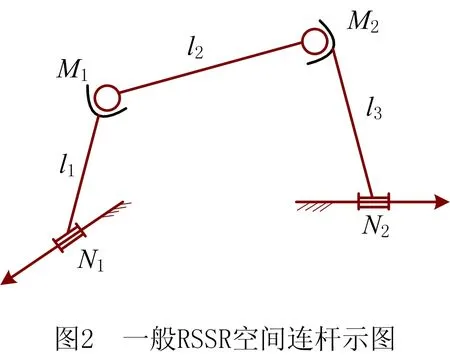
空间RSSR型机构是指含有两个球面副与两个转动副的空间四连杆机构。如图2所示为一般RSSR空间连杆机构示图，图中：N1、N2为转动副;M1、M2为球面副。

2.1 运动副间隙向量的区间表示

空间转动副如图3所示，以销轴几何中心建立空间局部坐标系，假设O1为轴套1所在的几何中心，O2为销轴2所在的几何中心。向量O1O2可用来表示轴套1与销轴2的间隙向量。空间球面副如图4所示，以球窝几何中心建立空间局部坐标系，假设O3为球头3所在的几何中心，O4为球窝4所在的几何中心。向量O3O4可用来表示球窝3与球头4的间隙向量。

空间RSSR机构共有2个转动副和2个球面副，O1O2、O7O8表示转动副模型中的间隙向量，O3O4、O5O6表示球面副模型中的间隙向量。运动副在装配、磨损后由于间隙的存在，在运动过程中会使杆件位置发生偏移。

假设x12、y12、z12表示间隙向量在空间转动副关节中的从第1个链环到第2个链环的空间坐标，则O1O2=[x12,y12,z12]T。设r12=|O1O2|，|O1O2|为O1O2的模长，由于间隙长度r12的值不确定，假设r12为三角模糊数，x12、y12与z12可用三角模糊数来表示，则区间向量O1O2被表示为：

(2)

当销轴与连杆中心重合时，r12存在最小值0；当销轴与连杆中心相距最远时，r12存在最大值(设为ε12)，则

r12=[0,γ12,ε12]。

(3)

式中：γ12为间隙圆中可能出现的半径；ε12为间隙圆中可能出现的最大半径。

当整个机构在运动过程中某一瞬时位置的间隙大小、位置确定时，三角模糊数对应的隶属度是确定的。设某瞬时位置对应的隶属度为λ，则x12、y12、z12与r12的三角模糊数可用向量的形式表示为：

(4)

(5)

O3O4、O5O6、O7O8和r34λ、r56λ、r78λ的表示类似，不再叙述。

2.2 转动副间隙的偏差区间模型

转动副关节间隙的偏差如图5所示，销轴与轴套在x,y,z坐标轴方向存在3个沿轴的相对平动和绕轴的3个相对转动。因为x轴建立在转动副的对称轴上，绕x轴的转动误差为0，所以空间转动副间隙在局部坐标系中的位移偏差可以表示为：

(6)

空间转动副关节的位移偏差Δδ12与转动副间隙向量O1O2的关系可以表示为

(7)

式中：Δx12、Δy12、Δz12表示间隙偏差在x,y,z方向上的位移;Δα12、Δβ12分别表示绕y，z轴的夹角;L为销轴的长度;φ为运动副中两元素(销轴与轴套)之间的夹角。

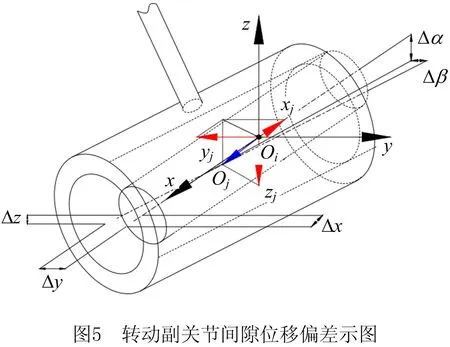
由于销轴/轴套的摆动角度φ的范围为0°～45°，则有

(8)

转动副关节间隙向量O7O8与位移偏差Δδ78的关系用公式表示与上面类似，不再赘述。

2.3 球面副间隙的偏差区间模型

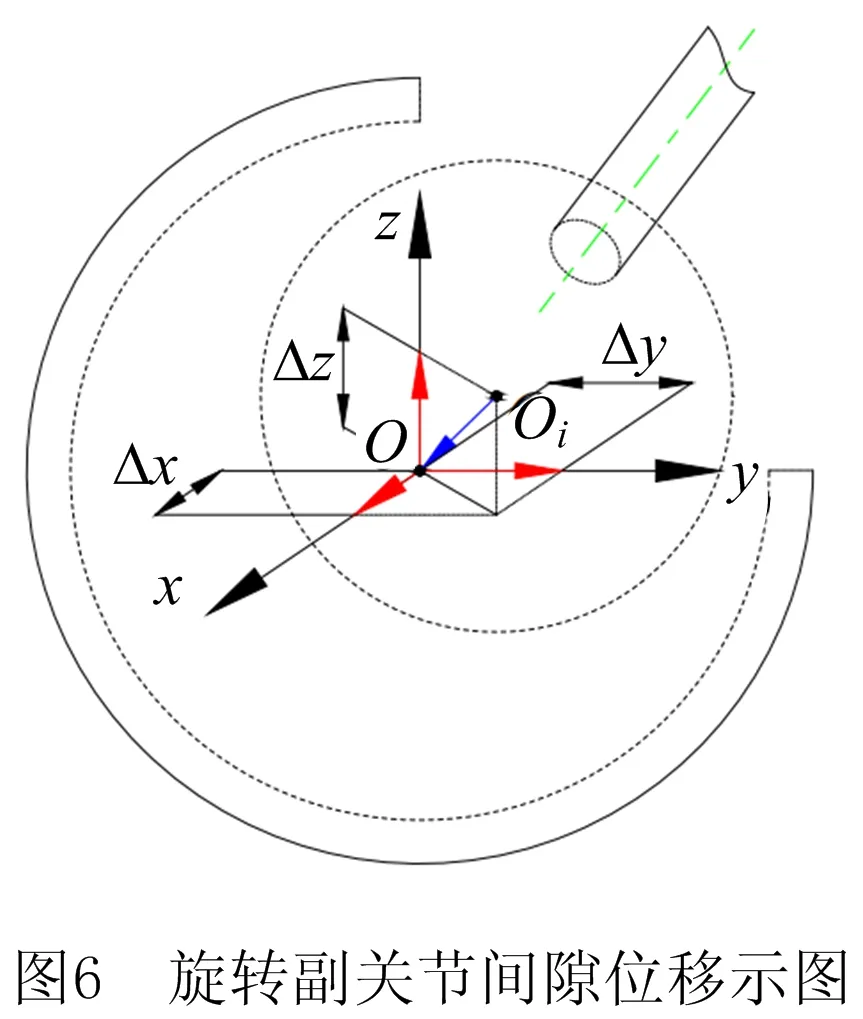
如图6所示，由于空间旋转副(球面副)限制了运动副关节中杆件在x,y,z方向上的位移，允许杆件以固定点绕x，y，z轴旋转。因此空间球面副的位移偏差仅存在x,y,z三个方向上的平移运动偏差，在局部坐标系中的位移偏差可表示为：

(9)

空间球面副关节位移偏差Δδ34与其间隙向量O3O4的关系可以表示为

(10)

式中：O3O4表示空间球面副的间隙向量；Δx34、Δy34、Δz34分别表示间隙在x,y,z方向上的位移偏差。

球面副关节间隙向量O5O6与位移偏差Δδ56的关系用公式表示不再赘述。

2.4 机构杆长偏差区间模型

(11)

式中：k=1,2,…,n，n为连杆的数量;λ为隶属度。

3 构建偏差回路与非线性区间参数方程组求解

3.1 构建偏差分析回路

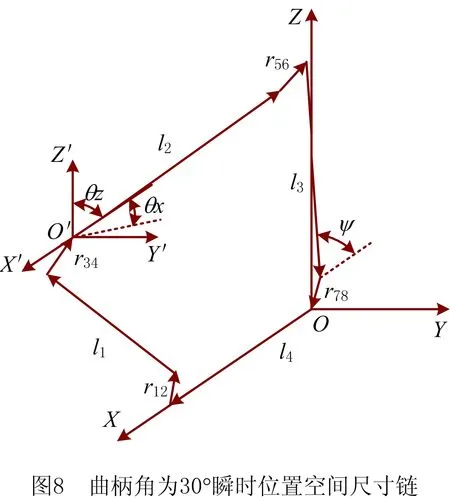
如图7所示为空间RSSR机构的向量模型，在固定空间坐标系OXYZ中，l1为RSSR机构的曲柄，其转动所在的平面为YOZ平面；曲柄角α转动范围为0°～360°，且规定曲柄角α=0°时(l1与z轴正方向夹角为0°)为初始位置；l2为机构的连杆，由于间隙的存在，其角位移大小与偏差未知；在球坐标系中，设连杆l3与x轴正方向的夹角为θx，与z轴正方向的夹角为θz，l3为机构的摇杆，其摆动所在平面为XOZ平面，摇杆摆角为ψ；l4为机构机架；设定空间RSSR机构各角位移输出值的偏差变动应满足：Δθx≤0.8°，Δθz≤0.8°，Δψ≤0.2°。

建立矢量回路：

(12)

式中：O1O2、O3O4、O5O6、O7O8表示关节间隙向量;k=1,2,3,…,n，n为连杆的数量;lk为所属连杆的空间向量。

为了简化偏差分析计算，空间运动副关节处的间隙采用局部坐标系的形式表示，对连杆l3矢量单独以球坐标系的形式表示，并采用矢量投影与平面投影的相结合的方法，用标量方程表示X、Y、Z方向的尺寸链回路方程为:

(13)

在建立了尺寸链回路方程后，将偏差的模糊区间数代入矢量回路方程可建立非线性区间参数方程组。

3.2 建立非线性区间参数方程组

空间RSSR机构各个杆件的尺寸及偏差范围如表1所示。

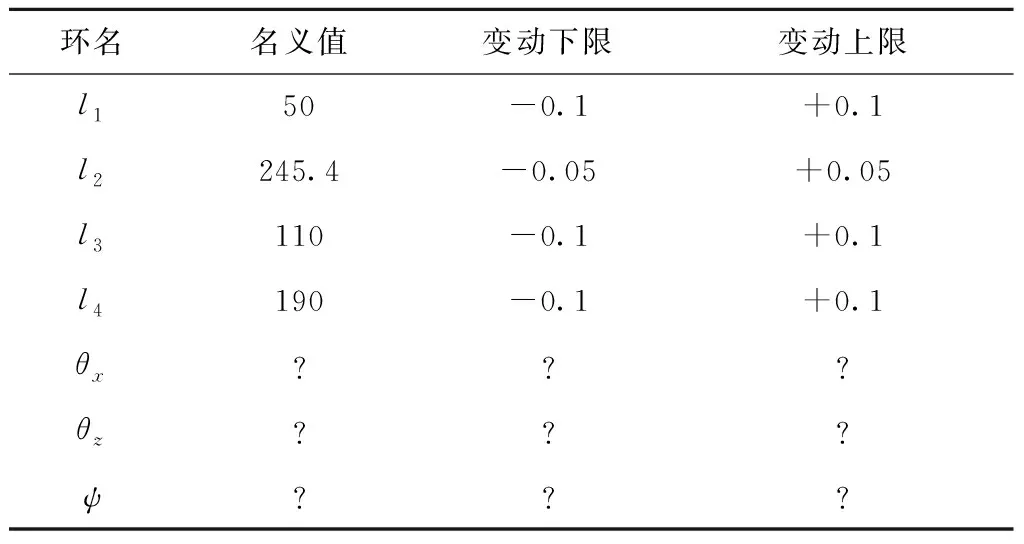
表1 空间RSSR机构杆件尺寸参数及偏差范围

引入三角模糊数隶属度λ，可将杆长偏差的变化情况表示为：

l1=[49.9+0.1λ,50.1-0.1λ],

l2=[245.35+0.05λ,245.45-0.05λ],

l3=[109.9+0.1λ,110.1-0.1λ],

l4=[189.9+0.1λ,190.1-0.1λ]。

(14)

式中λ为隶属度，0≤λ≤1。

如表2所示为运动副中各间隙参考值，则转动副关节间隙向量允许的最大范围为：

(15)

表2 运动副中各间隙值参考表

转动副在局部坐标系中的3个方向上位移偏差为：

(16)

根据式(8)，转动副绕y，z轴的最大偏角偏差为：

(17)

(18)

球面副间隙向量在局部坐标系中的3个方向上位移偏差为：

(19)

根据式(14)～式(18)，考虑隶属度的转动副和球面副关节位移变化范围可表示为：

x12=x78=[-0.002+0.002λ,0.002+0.002λ]，

x34=x56=[-0.002+0.002λ,0.002+0.002λ]，

y12=y34=y56=y78=

[-0.004+0.004λ,0.004+0.004λ]，

z12=z34=z56=z78=

[-0.004+0.004λ,0.004+0.004λ]。

(20)

式中λ为隶属度，0≤λ≤1。

选取曲柄角为30°瞬时位置作为分析对象，如图8所示为RSSR机构曲柄角为30°时的空间尺寸链。由于各杆件的尺寸误差分布范围的不确定性，按不同隶属度λ分为6种情况讨论。

(1)当λ=0时，非线性区间参数方程组可以表示为：

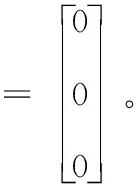
(21)

(2)当λ=0.2时，非线性区间参数方程组为：

(22)

(3)当λ=0.4时，非线性区间参数方程组为：

(23)

(4)当λ=0.6时，非线性区间参数方程组为：

(24)

(5)当λ=0.8时，非线性区间参数方程组为：

(25)

(6)当λ=1时，非线性区间参数方程组为：

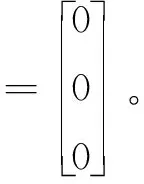
(26)

3.3 非线性区间参数方程求解

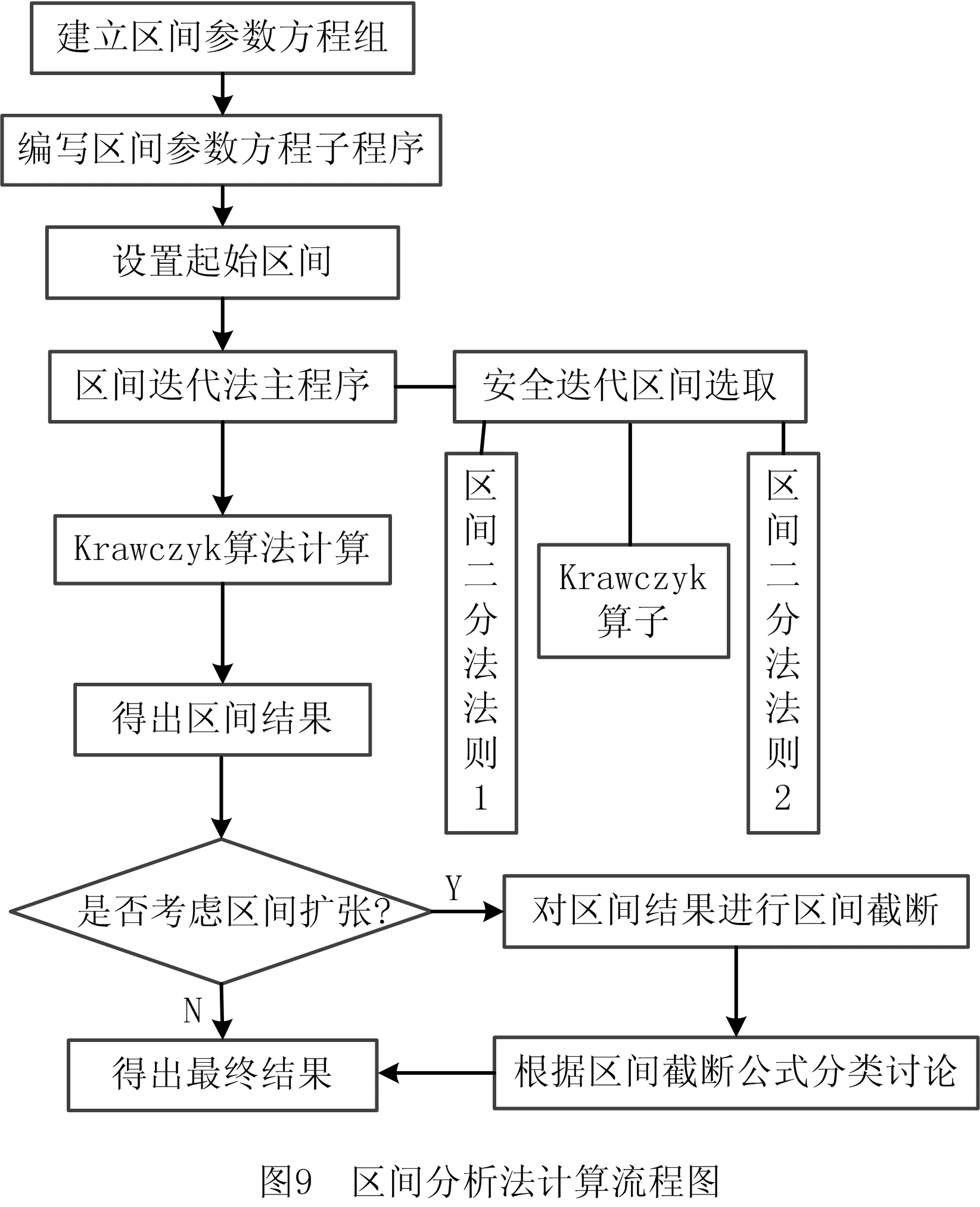
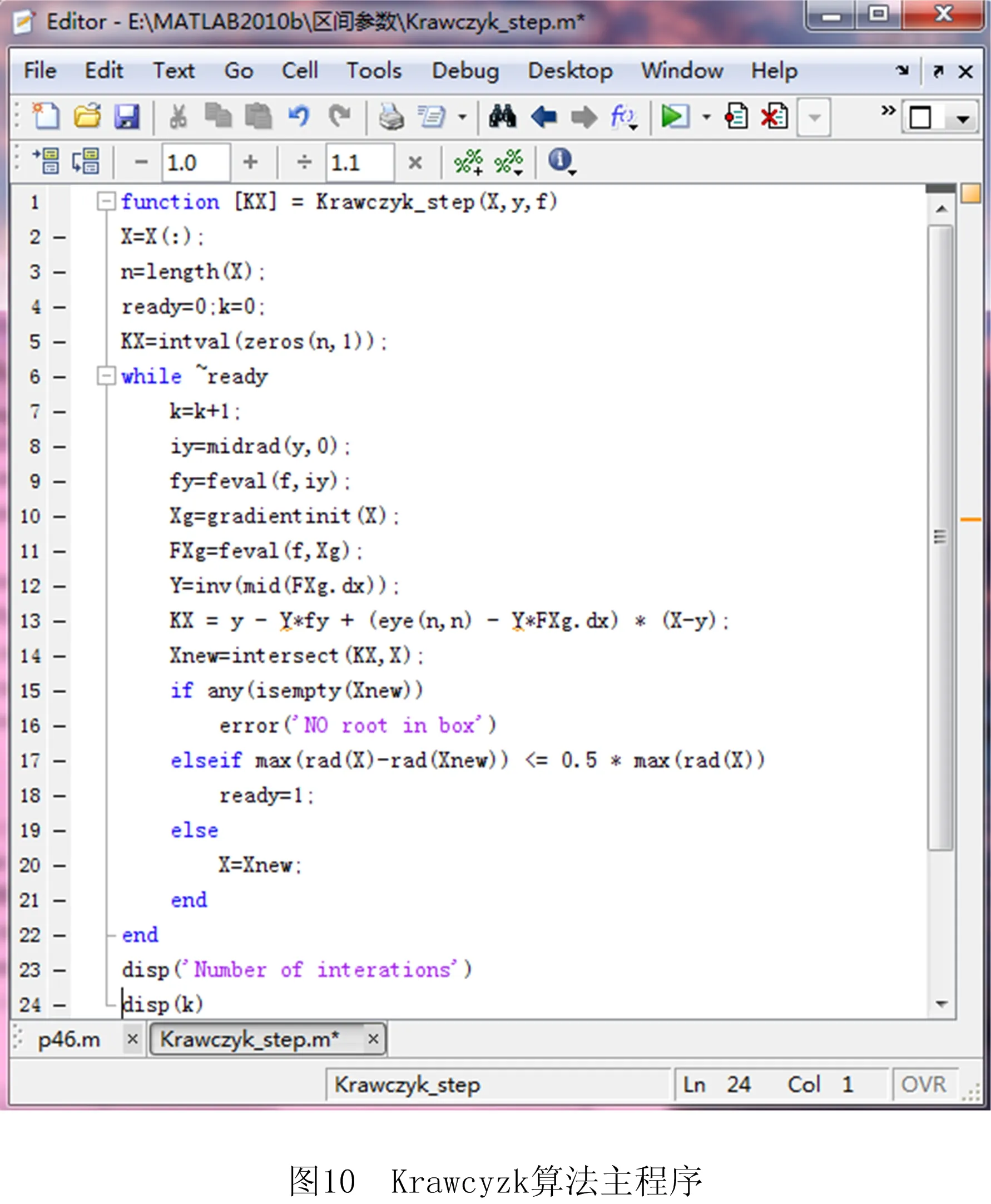
KRAWCZYK[13-14]在Moore的区间Newton算法基础上提出一种求解非线性区间参数方程的方法——Krawczyk算法，该方法避免了求逆矩阵，在工程应用中更符合实际要求。本文采用该算法的计算流程(如图9)，其中非线性区间参数方程组的求解在文献[15-17]中有详细介绍，使用MATLAB编写主程序(程序中插入了INTLAB工具箱)，如图10所示。

4 运动仿真与数值计算

运用UG软件对空间RSSR机构建立三维模型(各杆件的基本尺寸如表1所示)，通过添加相关特征来模拟机构中的运动副，并添加相应的物理约束条件，如图11所示。选取曲柄为驱动整个机构运动的动力输出杆，为了方便捕捉整个机构的周期性运动，设置曲柄初始位置(曲柄与基座垂直)状态，以STEP函数来驱动曲柄0°～360°逆时针运转，每隔30°设置一个瞬时位置，并且每个瞬时位置的间隔时间为4s，以便于测量相关输出角数据。

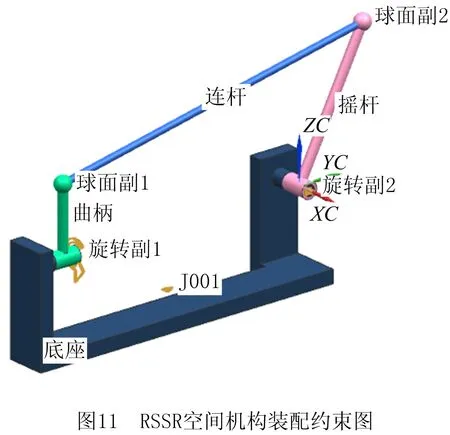
如图12所示为RSSR机构在曲柄角为30°瞬时位置的状态，选择UG软件自带跟踪测量工具，将连杆分别与设定绝对坐标中x，y，z三个方向上的输出角进行测量，同时测量摇杆的摆角。考虑到所设定绝对坐标系中的正方向，在某些瞬时位置的测量角度需要进行补角换算。在曲柄角为30°瞬时位置时，测量出各运动仿真输出角见表3，其余瞬时位置的输出角数值见附录表1。

表3 曲柄角30°时瞬时位置UG仿真输出角

采用第3章所述方法求解曲柄角为30°瞬时位置的非线性区间参数方程，所得结果如表4所示。曲柄角从0°～360°变化的各个瞬时位置，求解出的数值结果见附录表2～表4。

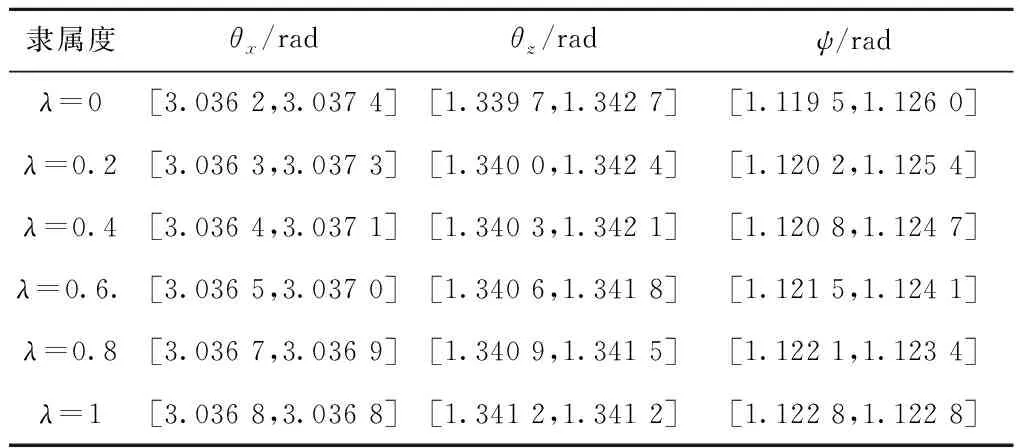
表4 曲柄角30°时瞬时位置的数值结果

因UG运动学仿真时未考虑间隙和杆长偏差的影响，其仿真出的输出角可认为是名义输出角，与采用区间分析法计算的结果进行对照，可绘制出输出角(角位移)与曲柄角的关系曲线。

5 空间RSSR机构偏差分析

将附表2～附表4的计算结果的变化趋势用图来表示，如图13～图15所示。图中3条曲线分别代表基本角度、角度偏差上限与角度偏差下限，其中基本角度为三维软件UG运动仿真分析出的结果，角度偏差的上限与下限为区间分析法计算结果。

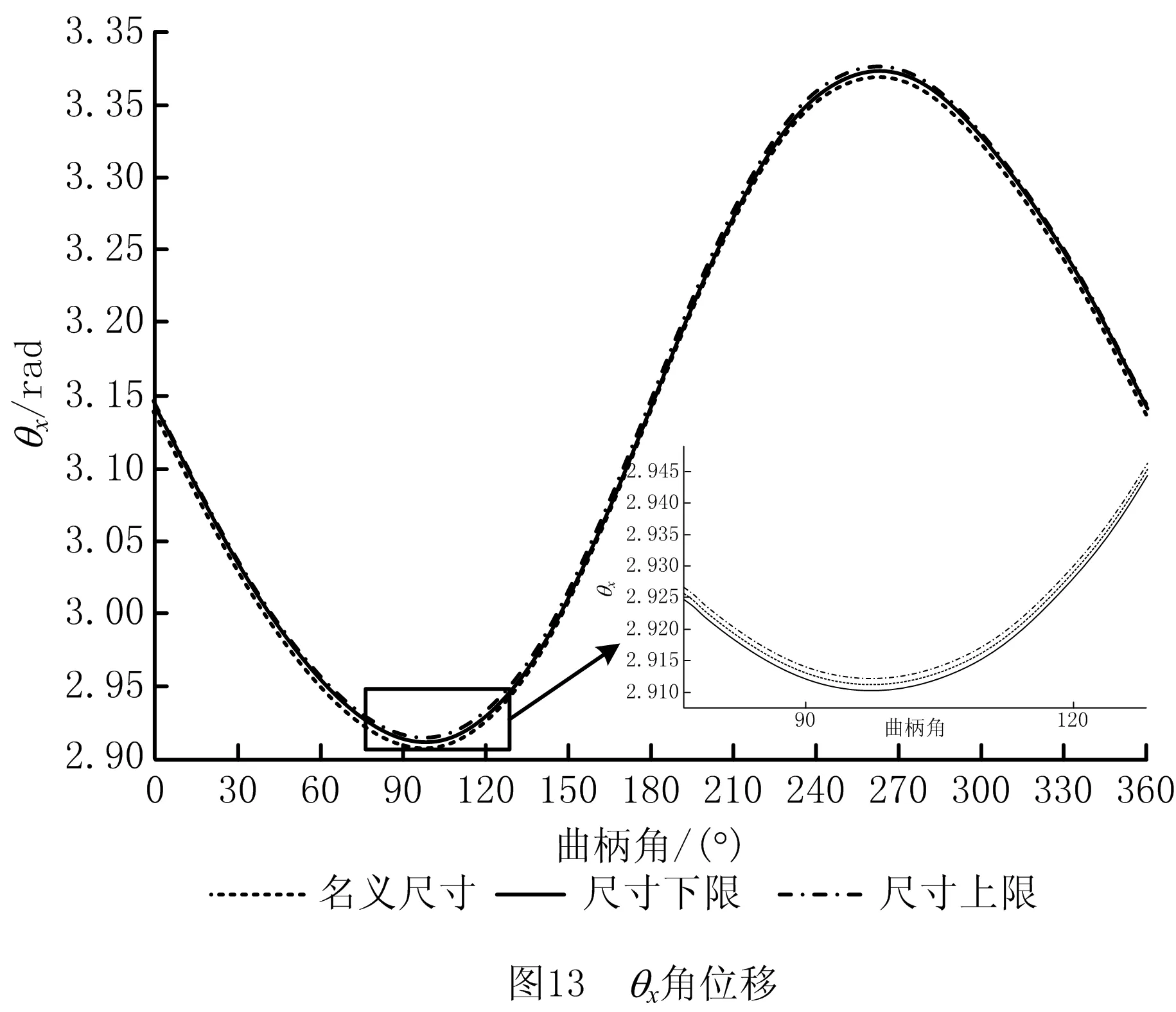
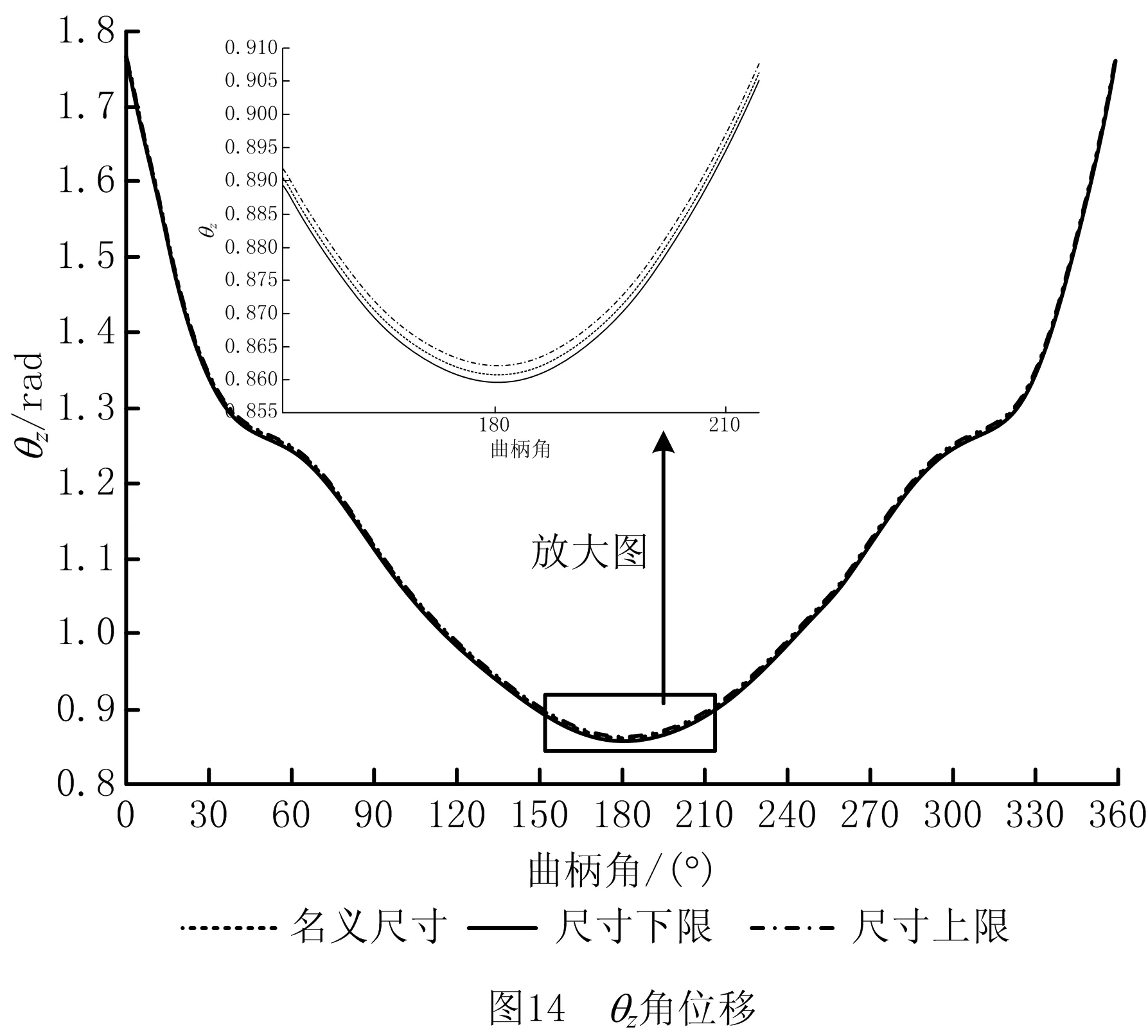
图16～图18是隶属度为λ=0时，θx角位移偏差、θz角位移偏差和摇杆角ψ角位移偏差变化趋势图。3张图均显示：曲柄角从0°～360°的变化过程中曲线整体呈大致对称的图形。从图16可看出：θx角位移的偏差值大小在曲柄角为180°附近受到的影响较为明显;从图17与18可看出：θx角位移和摇杆角ψ的角位移偏差值大小在曲柄角为90°与270°附近受到的影响较为显著。

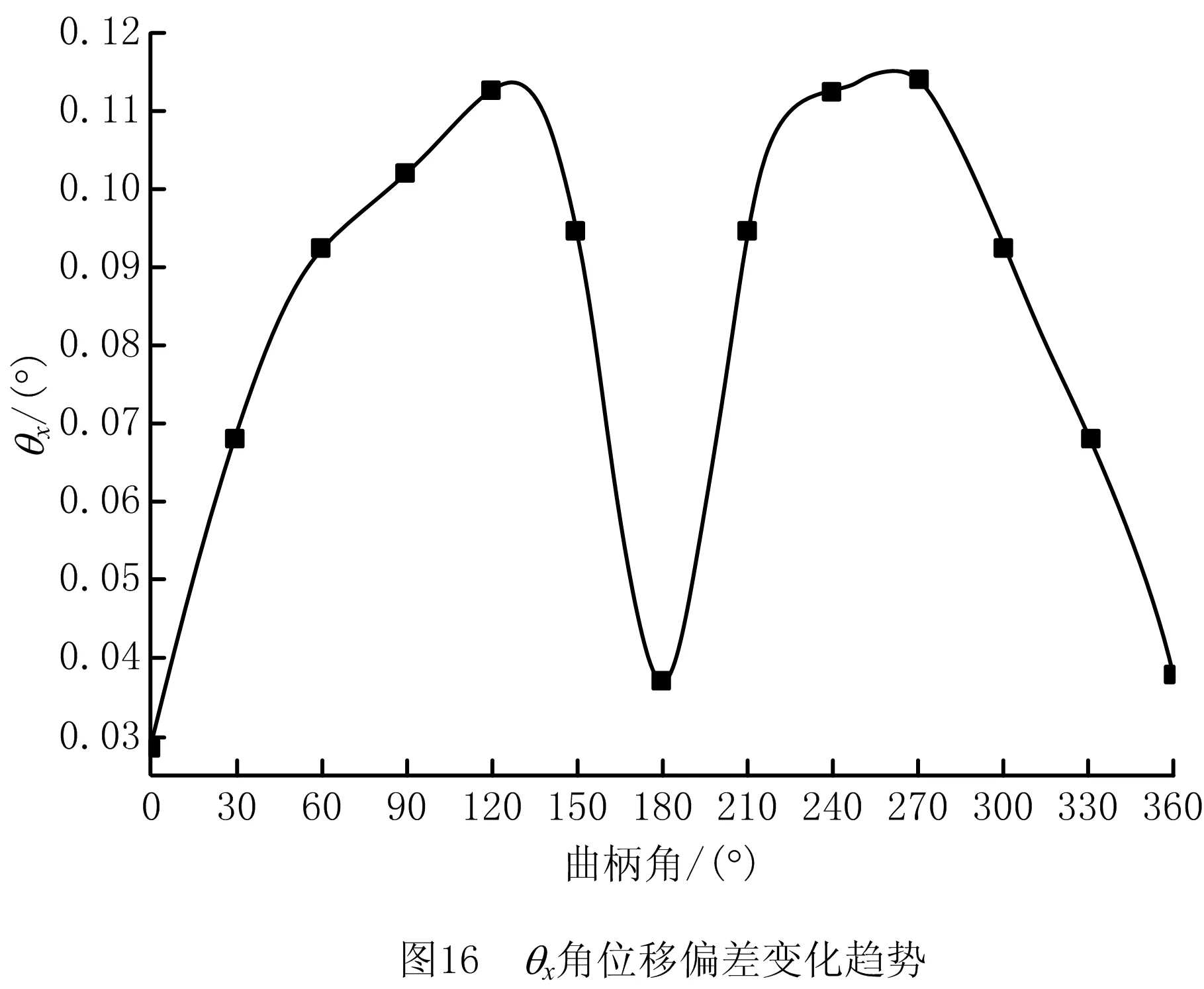
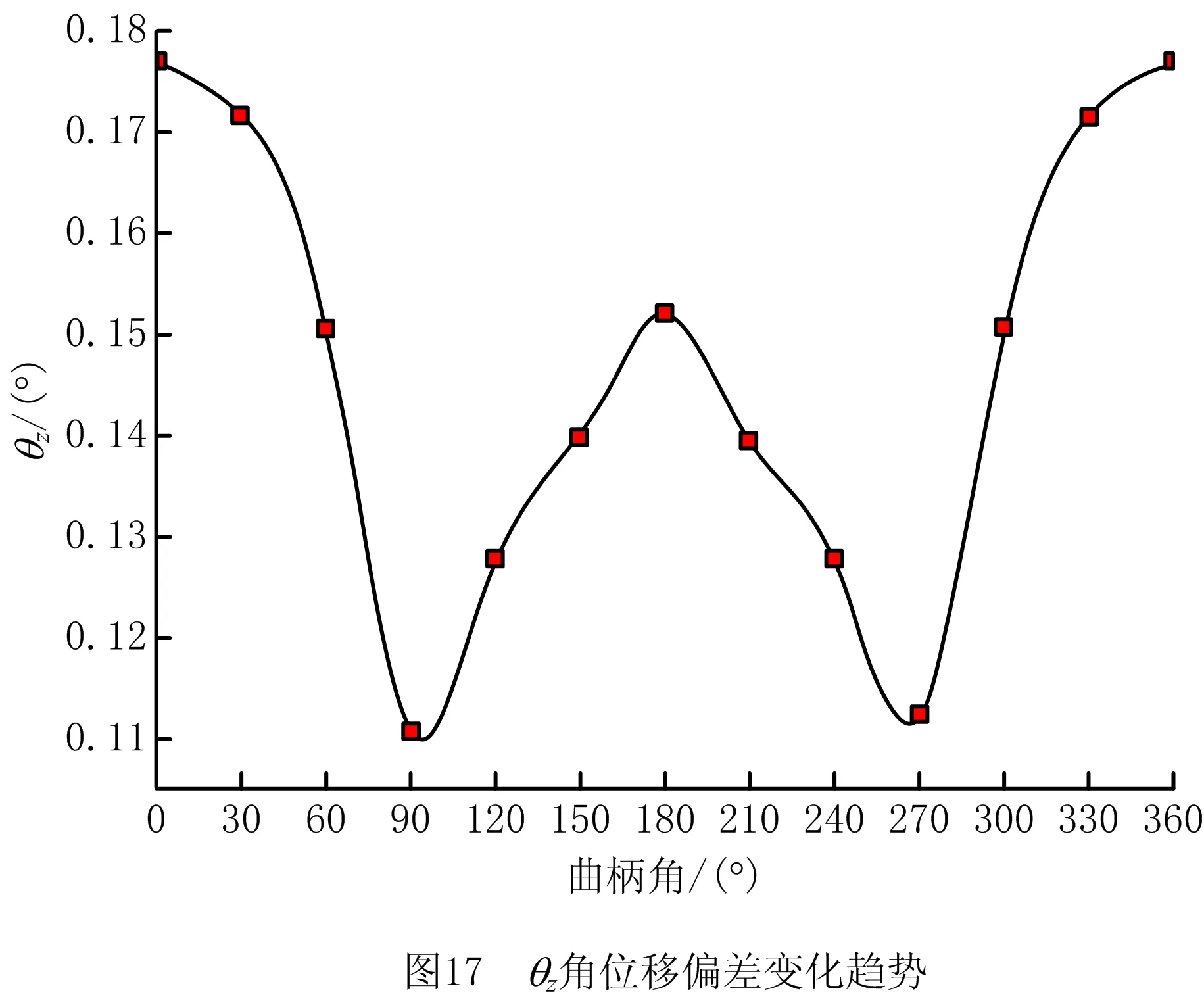
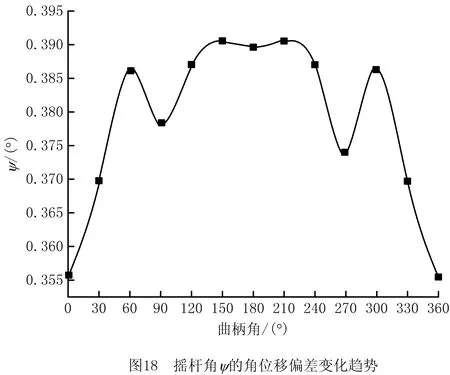
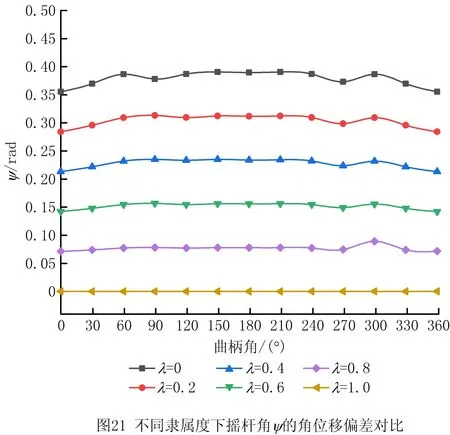
在引入隶属函数后，考虑了间隙大小与尺寸误差变化的情况下，得出如图19～图21的结果：

(1)由图19可以发现：当0≤λ≤0.8时，θx角位移的偏差值大小在曲柄角为180°附近受到的影响总是很明显，并且随着λ增大，θx角位移偏差值所受到的波动趋于平稳，影响就越小。

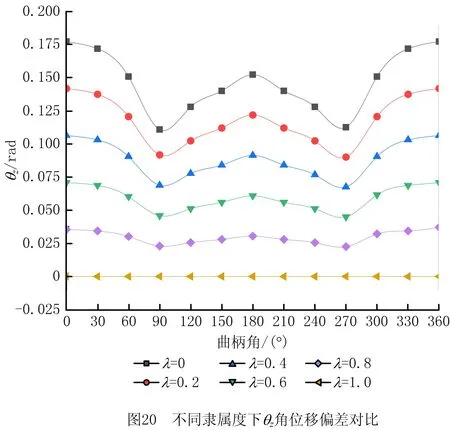
(2)由图20可发现：λ越小，θz角位移的偏差值波动越明显。

(3)由图21可发现：随着λ变小、间隙的增大，摇杆角位移偏差值也越来越大，但是偏差值的波动比较平稳。

总之，随着λ值的减小(间隙与杆长尺寸误差越来越来大)，θx角位移、θz角位移和摇杆角ψ角位移的极限偏差值的变化愈发敏感，并且波动的范围愈加明显。这意味着，磨损或者装配间隙增大对整个机构角位移的输出有着极大的影响。

若最初设定的杆长公差及运动副间隙大小(表1和表2，隶属度λ=0)对θx、θz以及ψ的输出影响较大，无法满足设计需求时需对隶属度进行优化调整。下面选取λ=0与λ=0.4两种隶属度进行偏差值变化情况对比分析(两种隶属度下杆长极限偏差数据如表5)，图22～图24所示为其输出角位移偏差对比图。

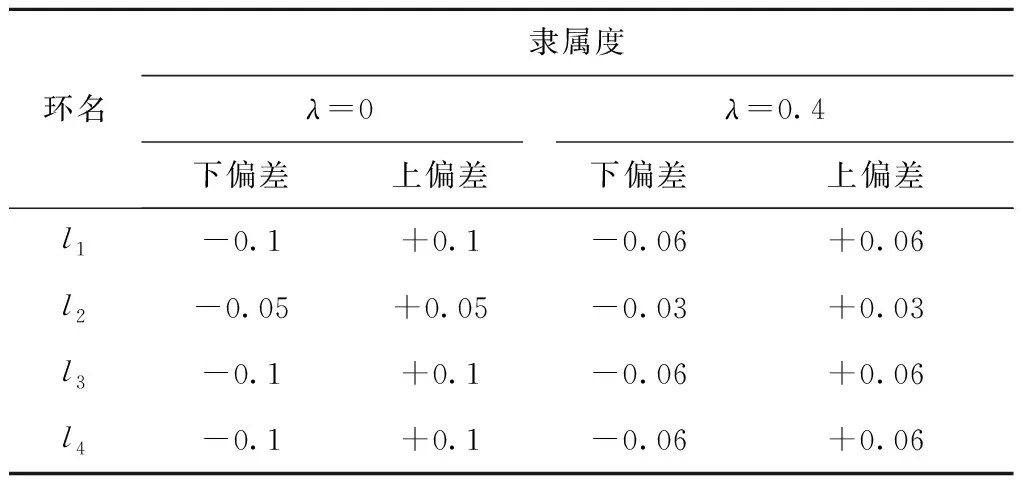
表5 隶属度为λ=0和λ=0.4时杆长极限偏差

由图22可得：隶属度为λ=0与λ=0.4时，θx的偏差波动情况如表6所示。

表6 θx偏差变动对比

由图23可得：隶属度为λ=0与λ=0.4时，θz的偏差波动情况如表7所示。

表7 θz偏差变动对比

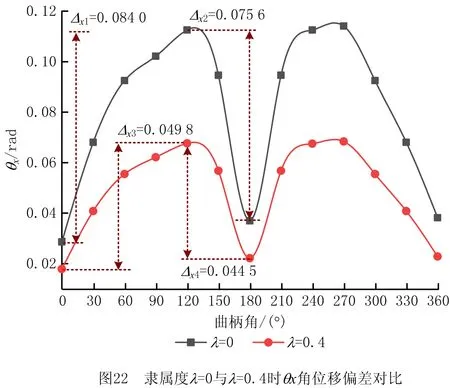
由图22和图23可看出：若隶属度从λ=0调整为λ=0.4，θx、θz角位移偏差值降低地较为明显，尤其是在90°、180°、270°转折处。

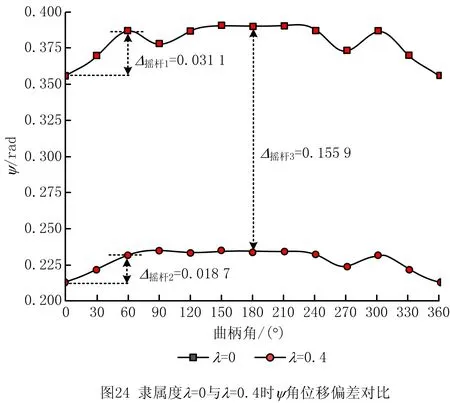
由图24可得，λ=0时Ψ偏差波动情况如表8所示。曲柄角0°～60°对应的偏差变化曲线波动不大；而从λ=0变化到λ=0.4后，Ψ偏差变化较为明显。例如，在曲柄角为180°时，其变化值可达Δ摇杆3=0.155 9。

表8 ψ偏差变动对比

从表6～表8中的角位移输出值偏差变动可得：隶属度λ=0.4时的偏差范围小于λ=0时的偏差范围；在附表2～表4中，隶属度λ值越小(即杆件的尺寸偏差越大)，角位移输出值的偏差范围就越大；当λ=0时，角位移输出值的偏差变动范围属最差情况；当λ=1时，角位移输出值的偏差变动范围属于理想化状态；而当λ≤0.4时，角位移输出值的偏差变动范围满足初始设定的偏差变动范围要求，故可将λ=0调至λ=0.4。

6 结束语

本文以空间RSSR曲柄摇杆机构为研究对象进行了偏差分析研究，不仅考虑杆长尺寸偏差，还考虑了运动副间隙的影响。因机构中的连杆尺寸误差和运动副间隙大小的变化具有一定的随机性，其变化规律或概率分布函数往往是无法获知的，而采用区间分析法能克服此缺陷，该方法求解尺寸链时无需知晓杆长或间隙的概率分布。基于该方法建立了空间RSSR机构的区间模型，采用矢量投影、平面投影等方法构建了偏差分析回路，建立非线性区间参数方程组，编制了求解非线性参数方程组的区间计算程序，并结合UG运动仿真进行了偏差分析。

引入隶属函数分析了机构在不同隶属度的瞬时位置杆长偏差和关节处间隙变动对连杆、摇杆角位移的影响。分析结果显示：连杆、摇杆的角位移偏差在机构运转输出角位移曲线的极大值点与极小值点附近的变化尤为明显。当隶属度从λ=0调整至λ=0.4，符合初始空间RSSR机构设定的角位移输出值的偏差变动范围，且此时机构角位移偏差波动幅度均明显降低，有利于保证机构的运动精度和平稳性。下一步，将在此基础上研究空间RSSR机构的公差设计与标注问题。