基于改进的二进制蚁狮算法的特征选择模型及应用
2021-08-12赵转哲叶国文刘永明
赵转哲,叶国文,张 宇,刘永明+,张 振,何 康
(1.安徽工程大学 机械工程学院,安徽 芜湖 241000;2.安徽工程大学 人机自然交互和高效协同技术研究中心安徽省新型研发机构,安徽 芜湖 241000;3.宿州学院 机械与电子工程学院,安徽 宿州 234000)
0 引言
在机器学习过程中,过少的特征输入会降低系统学习精度,过多则会引起“维数灾难”,因此,特征选择对于机器学习的效果影响很大。根据选择过程中使用评价函数不同的物理意义,其方法可分为过滤式(Filter)、封装式(Wrapper)、混合式(Hybrid)3种。其中过滤式作为一种常用的数据预处理过程,可以对不相关的噪声特征进行快速筛选,计算时间成本低;封装式是基于各种分类器的输出精度来评价特征子集,分类精度高于过滤式方法,得到的特征子集维数也较少,但计算成本较高;混合式则结合了过滤式与封装式方法各自优势,兼顾分类精度和计算效率[1],因而引起了国内外学者的重视。张洁等[2]提出一种基于遗传算法和径向基网络进行特征预选,同时与拉普拉斯评价标准结合,形成混合式特征选择算法模型,并将制造车间高度冗余的数据特征置于该模型中,结果表明该模型数据压缩能力与分类性能得到了提高;雷亚国等[3]将基于过滤式的新型距离评估技术与多个融合遗传算法的自适应神经模糊推理系统相结合,提出一种新型混合故障特征选择模型,通过轴承故障识别实验验证了有效性;CADENAS等[4]提出一种基于模糊随机森林算法的混合式特征选择算法,并用于处理模糊高维且低质量的数据集;LU等[5]针对在DNA微阵列研究领域基因表达数据特征尺寸过大的问题,提出一种基于信息增益与改进遗传算法相结合的混合式特征选择方法,实验结果表明该方法在提高基因数据识别率的同时还具有较高的鲁棒性,但算法计算复杂度与CPU耗时普遍较高;SINGH等[6]提出一种融合特征选择与特征加权的混合式特征选择模型。上述学者针对各种特征选择算法,在计算速度与精度方面提出了不同的改进方案,做出了重要贡献,但在普适性方面仍需进一步研究。
特征选择本质上属于0-1规划的组合优化问题,已被证明是NP(non-deterministic polynomial)难题[7],受生物体捕食策略和进化方式启发的智能计算算法在解决NP难题中有独特优势,因此有学者已尝试将其应用到特征选择中,如改进的蜻蜓算法[8]、二进制粒子群算法[9]等,取得了不错的分类效果。
MIRJALILI等[10]通过观察并模仿蚁狮在幼虫时期的捕食行为,提出了一种新型群智能仿生算法——蚁狮算法(Ant Lion Optimizer,ALO),由于该算法具有参数设置少、寻优精度高等特点,被国内外学者应用于求解各种优化问题[11-12]。
EMARY等[13]在连续型ALO算法的基础上首先提出了用于解决离散优化问题的二进制ALO算法(Binary ALO,BALO),但该算法在实际使用中存在易陷入局部最优、收敛速度慢等缺陷。基于此,本文提出将保护集策略和多种群并行迭代的改进型二进制蚁狮算法,并将该算法结合混合式特征选择模型应用到UCI(University of California Irvine)标准数据集与滚动轴承故障集的特征选择实验中,以提高机器学习模型的识别精度,同时提升特征约简能力。
1 标准二进制蚁狮算法
1.1 算法基本思想
蚁狮的猎捕过程经简化并抽象后,可分为5个阶段,即蚂蚁的随机游走、蚁狮的陷阱挖掘、蚂蚁落入陷阱、蚁狮捕食蚂蚁、陷阱重建[10]。如图1a所示为蚁狮在土地上挖出大小不一的陷阱。由于蚁狮了解蚂蚁的行踪轨迹,蚁狮在构筑陷阱时会确保蚂蚁在陷阱附近进行随机游走。蚁狮幼虫在挖好陷阱后,便蹲守在陷阱底部等待附近游走的蚂蚁落入陷阱,此过程如图1b所示。

1.2 数学模型
BALO算法将蚂蚁与蚁狮个体的各个维度取值限制为0或1,并加入了遗传算法中的交叉算子,对蚂蚁位置进行更新:
X(t+1)=Crossover(Rrs(t),Re(t))。
(1)
式中:X(t+1)表示第t+1代的新蚂蚁个体;交叉操作Crossover通过轮盘赌选择蚁狮Xrs(t)与精英蚁狮Xe(t)位置附近游走获得两个二进制解Rrs(t)、Re(t)。该交叉操作在X(t+1)的各个维度的具体实现形式如式(2):
(2)
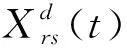
(3)
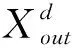
(4)
2 改进的二进制蚁狮算法
2.1 改进策略与数学模型
在BALO的标准流程中,由于蚁狮个体对蚂蚁个体的替换机制,导致算法在每次迭代末期,将生存能力较差的蚂蚁个体直接从群体中剔除,种群规模的突然缩减不仅使得种群个体的多样性急剧下降,使得具有搜索潜力的个体丢失,还会因此导致算法全局搜索能力降低、易早熟等缺陷的产生。基于此,本文提出基于保护集策略与多种群并行迭代的改进型二进制蚁狮算法,记作IBALO(improved BALO)。通过引入种群保护集策略,对尚未表现出潜力的个体进行捕捉与保护,防止在种群迭代中被遗失,可以提高种群的多样性与抗干扰性;使用多种群并行迭代的特点,可以提高算法的收敛速度,更快速地获取问题的最佳解决方案。
(1)保护集策略 在BALO中,蚁狮群体属于强势群体,蚂蚁群体为弱势群体,模拟算法的迭代过程即是蚂蚁被蚁狮捕食取代的过程,在群智能算法中,更多的思想是考虑群体之间的共同进化,如粒子群算法是在鸟群个体之间进行食物信息共享,从而使群体错落有致、方向明确地前往食物地点;算法的迭代过程可以视作群体之间相互协作,实现互利共赢的过程,算法中个体无论优劣,都会在迭代中被引领而逐步进化,而非由于适应度值过低而直接淘汰出局。
因此,本文对蚂蚁群体进行部分保护,以免部分具有寻优潜力的个体被忽视。在各代种群适应度排序结算完成后,以适应度作为一定的权重,在蚂蚁弱势群体中选拔部分蚂蚁个体进入保护集内进行暂时保护,且适应度优良的个体更容易进入保护集,为了引领该集合内个体发挥自身潜能,选取部分拥有特征数较少的蚁狮个体进入保护集。
(2)多种群并行迭代策略 在求解复杂优化问题时,为了提高算法代码执行效率和精确性,可以对算法进行并行化处理[14]。LAMPINEN等[15]对差分进化算法种群进行多种群并行化处理,各个子种群互相独立,在相同的代数间隔下各子群通过相互沟通寻找这些子种群中存在的适应度最优值,以达到搜索精度要求。本文借鉴其核心思想,对BALO种群分为两个子种群进行并行执行,以提高算法收敛性能。
为了与原算法群体加以区分,以保护集为初始父本产生的集合称为次群,原算法种群称为主群。在接下来的迭代中,次群中的所有个体采取与主群相同的方式产生轮盘赌选蚁狮,并进行随机游走更新次群中蚂蚁群体(为了使次群集合有着良好的进化方向,次群中精英蚁狮仍使用主群中的Xe);主次群迭代完成后,所有个体融合成一个总集合,并进行适应度评估。
上述两种策略在融入算法的过程中互相依赖,相辅相成。在每次算法迭代循环末期,要求程序对主、次种群按适应度进行排序划分,模型如式(5):
mixp=mp+sp=gi+wi。
(5)
式中:mp表示主群集合;sp表示次群集合;mixp表示主、次群构成的总集合;gi表示mixp排名靠前的个体集合;wi表示mixp排名劣势的个体集合,且下一代以gi为父本产生mp;对保护集策略中提到的排序与筛选方法模型如式(6)~式(9):
rankc=sort(fc(gi));
(6)
rankv=sort(rmat·fv(wi));
(7)
(savev,savec)=extract(rankv,rankc);
(8)
save=savev+savec。
(9)
其中:rankc、rankv分别表示按特征数个数与拥有适应度值大小排名后的个体集合;fc()为统计特征个数的算子;fv()为统计适应度值的算子;sort()为按参数的适应度排序的算子;rmat为一个包含0~1之间随机数的矩阵,随机数个数与fv(rpt)包含值的个数保持一致;extract()为提取前20%占优个体的算子,将savec与savev储存到表示保护集的save变量中,并作为下一代sp的产生依据。
2.2 实现步骤
IBALO的实现步骤如下:
(1)IBALO初始化参数。种群维度、规模,最大迭代次数等。
(2)种群初始化。由于IBALO针对二进制0-1组合优化,故在仅含有0,1的边界集合中随机选取并对蚁狮、蚂蚁进行种群初始化。
(3)计算适应度值并排序。计算各个蚁狮的适应度并排序,记录全局最优蚁狮Xe。
(4)对各个蚂蚁进行位置更新(主群迭代开始)。分别使用轮盘赌法选择蚁狮Xrs和精英蚁狮Xe,并在其周围使用变异操作进行随机游走,得出Rrs、Re。
(5)对Rrs、Re使用交叉操作更新蚂蚁的位置,计算更新后蚂蚁适应度,并与原有蚁狮进行合并得到mp,按适应度进行排序。
(6)若当前迭代次数t=1,转步骤(7),且此时次群视为空集;若t>1且不大于T,进入次群迭代:以save中的个体为父本,对次群蚂蚁进行同步骤(4)和步骤(5)的位置更新操作,为了使sp有良好的进化方向,精英蚁狮仍使用Xe,把得到的蚂蚁群体与来自上代的save进行合并产生本代sp集合,次群创建完成后转步骤(6)。
(7)将mp与sp合并得到mixp并按适应度排序,由式(5)得到gi与wi,从gi中提取一定的种群保护百分比p个特征最少的个体为savec,提取wi中按适应度权重随机选择相同百分比的p个适应度最好个体为savev,二者组合为保护集save。
(8)提取mixp中最优个体与Xe进行比较,若优于Xe,则Xe以最优个体进行替换。判断是否超过最大迭代次数T,若超过则算法结束,反之则转步骤(4)循环执行。
综上所述,得到IBALO流程图,如图2所示。
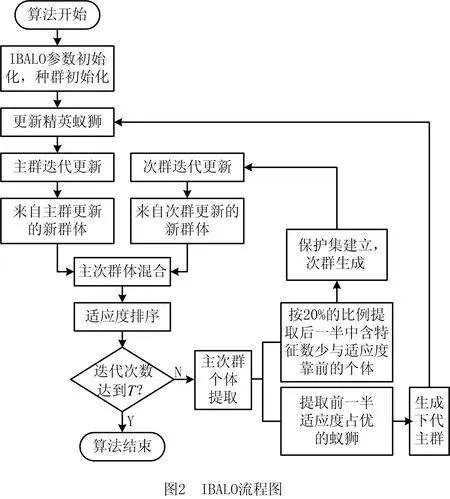
2.3 算法性能测试
为验证改进后的二进制蚁狮算法的性能,将典型整数规划问题的0-1背包问题[16]用于对IBALO算法的测试,该问题模型如式(10):
(10)
s.t.
xi∈{0,1},i=1,2,…,D。
其中:D为物品的总数,设为20;xi为旅行者选择第i种商品,且对应重量为wi、价值为qi;具体设W={wi}={92,4,43,83,84,68,92,82,6,44,32,18,56,83,25,96,70,48,14,58};Q={qi}={44,46,90,72,91,40,75,35,8,54,78,40,77,15,61,17,75,29,75,63};V表示最大承重,V=878。
实验中,用标准BALO算法进行对比,设种群规模A=300,最大迭代次数设T=300,种群保护百分比p=20%且各算法独立运行30次,平均迭代曲线如图3所示,统计结果如表1所示。
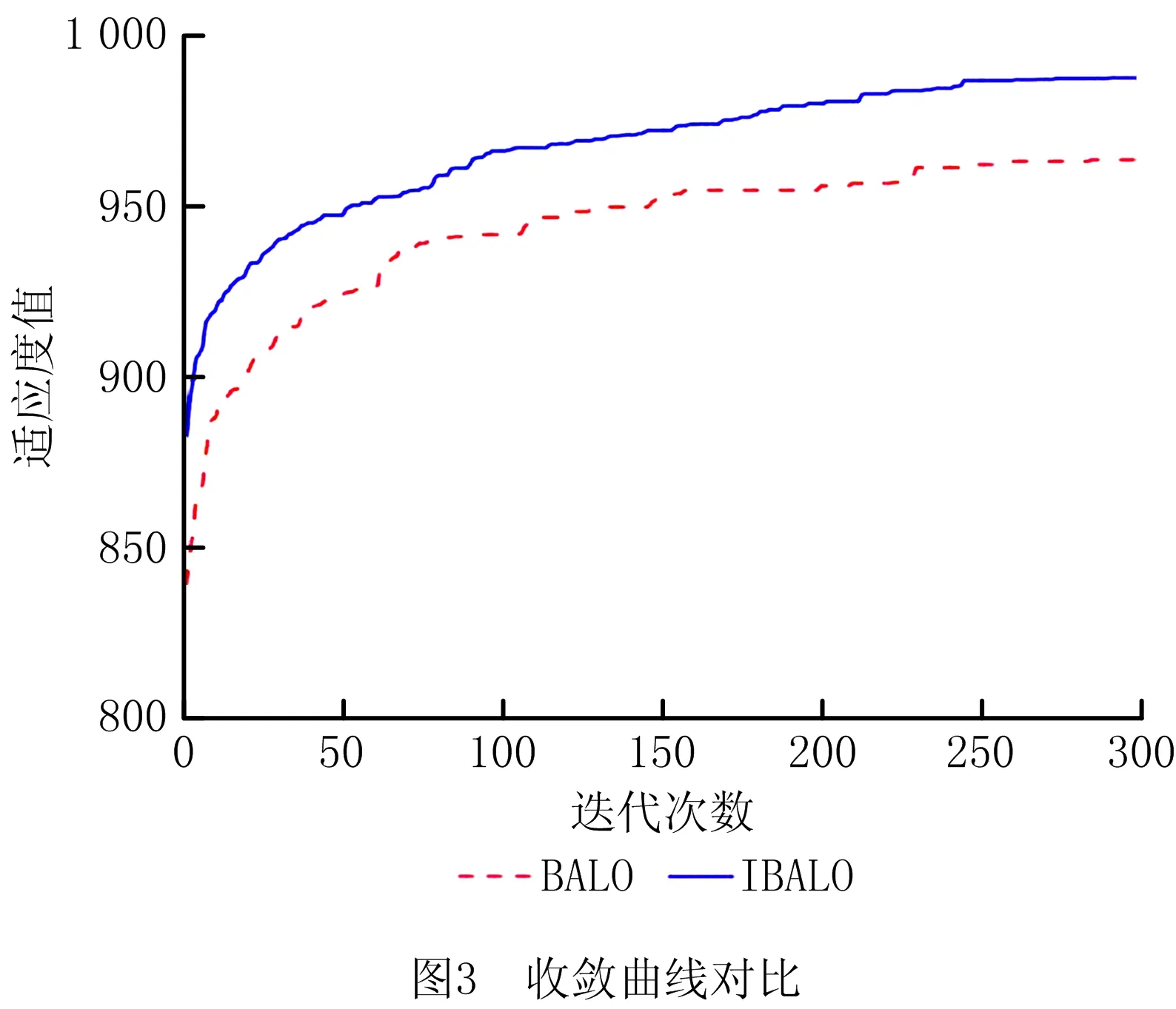
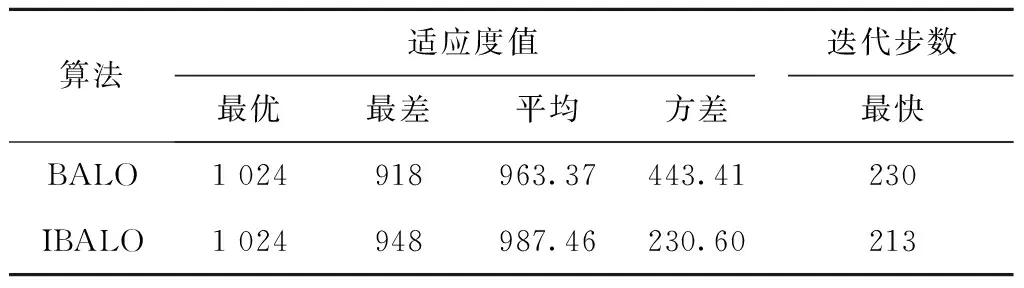
表1 优化结果比较
由图3可以看出,IBALO在整个收敛过程中适应度值皆优于传统BALO,这表明改进算法寻优精度较高;由表1可知,两算法最优值皆能达到文献[16]所述的理论最优值1 024,但改进算法不但所需迭代步数较少,算法收敛速度较快,而且方差较小,算法稳定性较高。综上所述,改进算法IBALO在提升收敛精度的同时,收敛速度与算法稳定性也有较为明显的提升。
3 融合IBALO的特征选择模型
3.1 混合式特征选择模型
为了更有效地对特征数据冗余进行筛选,本节提出一种基于IBALO的Hybrid式特征选择算法模型。在Filter式特征选择中,使用最大相关最小冗余理论[17](Minimal Redundancy Maximal Relevance,MRMR)对特征子集进行预选;在Wrapper式特征选择中,IBALO被用于进一步减少特征冗余以选择最优的特征子集。上述混合式特征选择算法的流程如图4所示。
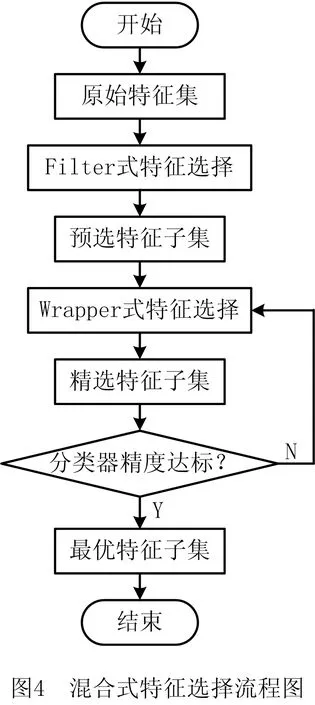
3.2 实现步骤
(1)基于MRMR的Filter式特征选择步骤
为增加提取特征有效性,该阶段使用基于互信息理论的MRMR准则,以分类器精度最优构造评价函数,实现Filter特征筛选。具体步骤如下:
步骤1设原始特征集为S且包含特征个数为u个,使用MRMR准则构造出特征排序集合Sq,并记qz为排序序号为z的特征值:
Sq={q1,q2,…,qu}。
(11)
步骤2将特征排序集合Sq的子集i记作Sqi,对Sq以每次递增一个特征的形式构造特征子集Sqi并输送到分类器中(本文选取5-近邻分类器)计算其分类精度,如式(11):
(11)
步骤3以分类结果绘制分类精度曲线,设置横坐标为特征数,纵坐标为分类精度。记录曲线达到最高点时对应的特征数,并以此为依据舍弃其他无关特征,进而得到过滤除杂后的特征子集Sf。
(2)基于IBALO的Wrapper式特征选择步骤
在这一阶段,为了进一步降低特征冗余,将Sf作为Wrapper型特征选择的输入,并在该过程中融入IBALO,以分类器分类精度作为IBALO的适应度评价标准,以算法迭代结果确定最终的最优子集,实现Wrapper式特征选择。具体步骤如下:
步骤1对IBALO进行适应度函数构建。将特征子集Sf与分类器进行连接并置于适应度函数内。
步骤2IBALO的参数初始化、种群初始化等,鉴于特征选择属于0-1组合优化问题,故种群初始化每个个体含有一组0-1字符串,0代表舍弃该特征,1表示选择该特征。
步骤3对IBALO进行算法迭代,当达到最大迭代次数时,算法停止寻优,并给出适应度最优的特征组合。
上述两个阶段组成的混合式特征选择算法模型记为MRIBALO。
3.3 模型性能测试
本实验从UCI数据库[18]中提取了6个不同特征数数据集对上述模型性能进行测试,其中数据集的特征数最低为21,最高为60,具体信息如表2所示。另外,本实验随机抽取总样本的3/4作为训练样本,剩余1/4作为测试样本。
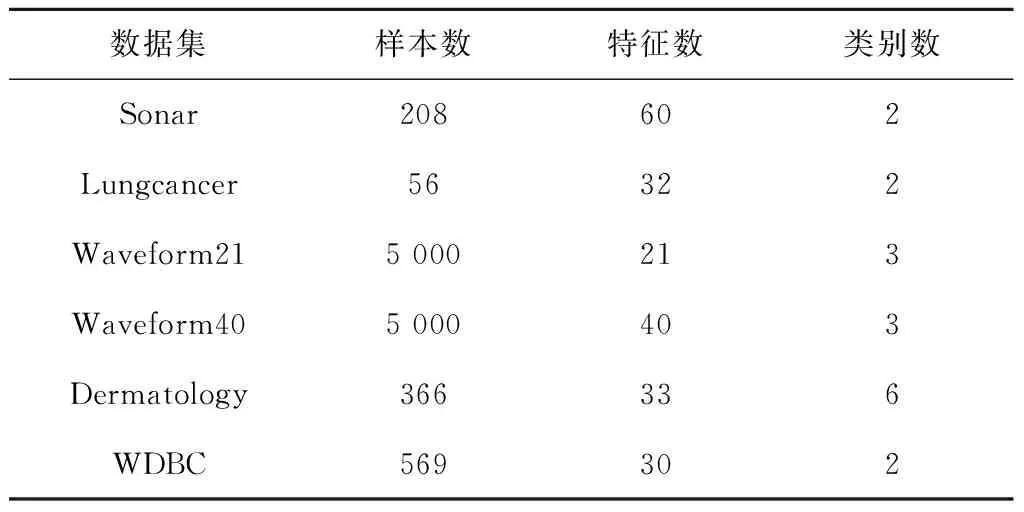
表2 测试用UCI数据集详情表
以平均识别率最大为目标构建适应度函数,其中TRi表示某数据集中第i类数据的识别率,c表示该数据集所含类别的个数:
(12)
为突出MRIBALO的优势,本文结合基于MRMR准则的Filter式的特征选择算法(MRMR Feature Selection,MRFS)与基于传统的BALO混合式特征选择算法(记为MRBALO)进行对比实验,参数设置如下:设种群规模A=30、最大迭代次数T=50。为避免偶然性误差,各算法在每个数据集上需要独立运行20次,实验对比结果如表2所示。
如图5所示为各个数据集通过Filter式特征选择方法——MRMR准则得到的序列特征子集数的识别率曲线。可以看出,算法识别率未必随着特征数的增多而增大,这说明在原始特征集中含有影响分类精度的冗余特征,各个曲线最佳特征集的提取与曲线峰值记录在如表3所示的MRFS算法对应栏中。
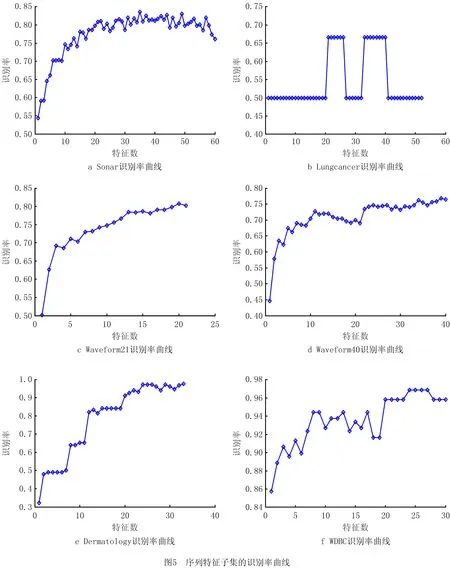
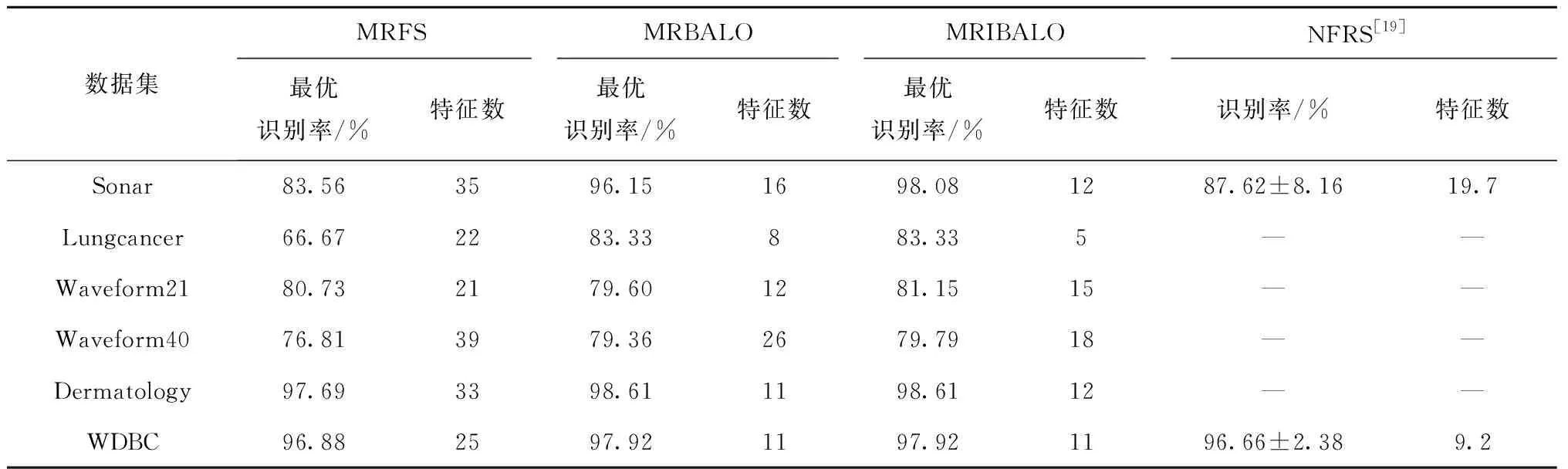
表3 不同算法实验结果对比
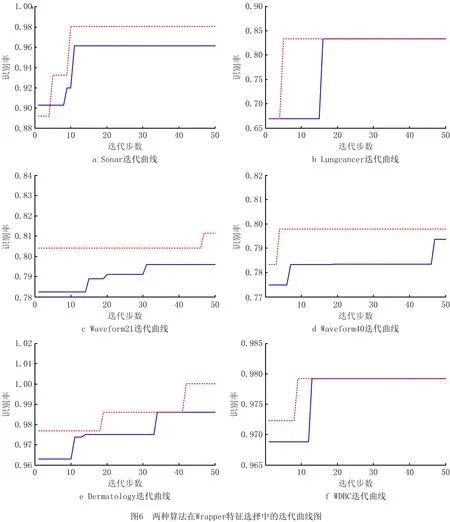
如图6所示为使用基于MRBALO与MRIBALO的Wrapper式特征选择算法在6种测试集上的收敛曲线对比。可以明显看出,经过改进后的MRIBALO拥有更高的收敛速度、识别精度与鲁棒性。
由表3可知:
(1)从识别正确率的角度看,基于混合式特征选择的MRBALO与MRIBALO得出的最优识别率整体高于MRFS算法,虽然在WDBC这个数据集中,与基于新型模糊粗糙集(New Fuzzy Rough Sets, NFRS)的约简方法效果近似,但在Sonar数据集中,其识别率最高仅为95.78%,低于MRBALO与MRIBALO模型,这印证了基于蚁狮优化算法的混合式特征选择模型的有效性。其中,MRFS、MRBALO和MRIBALO三个模型相比,MRIBALO的整体识别率表现最好,提升幅度分别为14.52%、16.67%、0.42%、2.98%、0.92%、1.04%。
(2)从特征约简维数的角度看,基于蚁狮优化算法的二次寻优大幅度减少了特征维数,相较于MRFS的约简得到的特征数,MRIBALO模型的特征缩减比例分别为65.71%、77.27%、28.57%、53.85%、63.63%、56.00%。相较于MRBALO,基于改进二进制算法的MRIBALO模型在Sonar、Lungcancer、Waveform40这3个数据集中特征缩减比例分别25%、37.5%、30.77%,其中,NFRS模型虽然在WDBC数据集中约简维数平均值小于MRIBALO模型,但实质上差别不大;在Sonar数据中,MRIBALO模型约简能力更强,与NFRS模型相比,缩减比例为39.08%。以上数据表明了本文提出的特征选择MRIBALO模型在提升识别率与约简特征维数方面的有效性。
4 滚动轴承故障诊断实例
4.1 数据来源
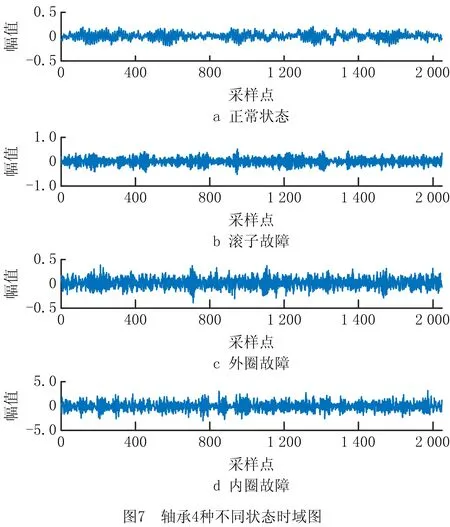
本章采用来自美国凯斯西储大学滚动轴承故障模拟平台驱动端的故障数据[20],实验采用电火花技术对轴承的不同部位造成不同尺寸大小的损伤以对滚动轴承的早期故障进行模拟,并使用加速度振动传感器对轴承振动信号进行采集,采样频率为12 kHz,选取轴承损伤分别位于滚子、外圈、内圈与正常轴承共4类振动信号数据构成故障特征原始数据集,其时域波形如图7所示。另外,设各组数据对原始数据的采样点数均为2 048。
4.2 特征集构造
对滚动轴承振动信号的故障诊断,已有很多信号处理方法提取的特征被证明有效,如时域、频域、以及时—频域特征等。但是单纯以某类特征作为性能评判指标不能全面地反映滚动轴承的退化信息[21-22]。基于此,本文选用57个特征构建混合特征集,其中包括峰值、方根幅值、方差、标准差、偏度、峭度、绝对均值作为时域特征;重心频率、均方频率、频率方差作为频域特征;时—频域特征提取方面,考虑到提取轴承特征信息的有效性,对轴承故障信号分别取前30个奇异值特征,记为[λ1,λ2,…,λ30];三层小波包分解的8个频带能量特征,记为[E30,E31,…,E37];基于局部均值分解(Local Mean Decomposition,LMD)得到的前3个PF(product funtion)分量的符号熵特征,记为[PF1,PF2,PF3];基于变分模态分解(Variational Mode Decomposition,VMD)得到的前6个IMF(intrinsic mode function)分量的符号熵特征,记为[IMF1,IMF2,…,IMF6],上述特征构成的混合特征集具体参数如表4所示。
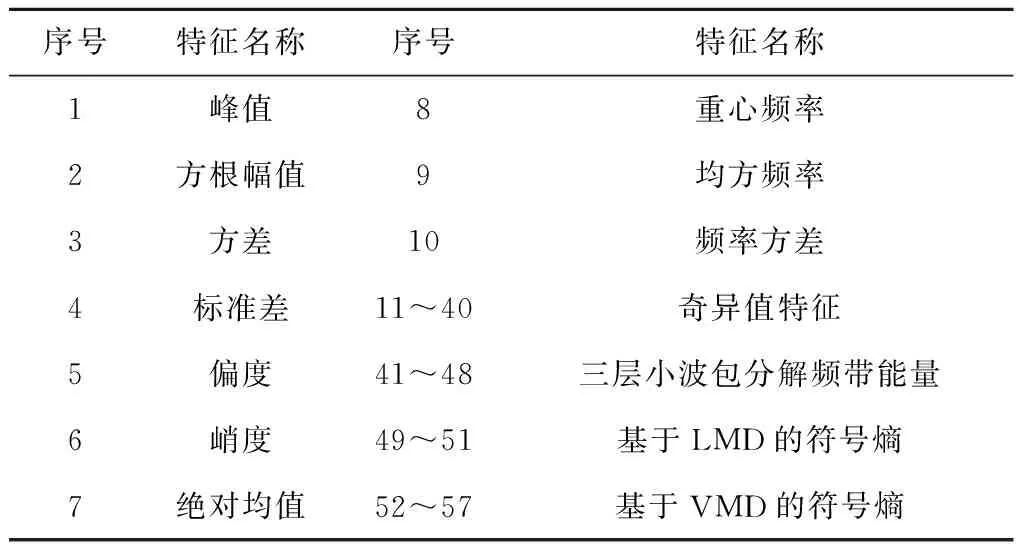
表4 特征集特征名称与序号
对混合特征集分别使用MRFS,MRBALO以及MRIBALO对上述轴承故障数据集进行故障诊断。公平起见,算法初始参数均设为:A=50、T=50,实验采用5-近邻分类器对特征进行故障识别,考虑到偶然性因素,MRBALO与MRIBALO算法的Wrapper过程各个独立求解20次。对4类轴承样本每个样本各取50组,且训练集与测试集之比为4∶1。
特征选择要求特征子集经过分类算法后得出的识别率好,且特征子集维数较少,即最大化识别率和最小化特征子集大小。考虑多目标优化的适应度函数可以用权重法转化为单目标求解,设置适应度函数如式(14):
(14)
式中:γR为所有类别分类正确率均值;N为总数据集中特征数;L为实验得出最优特征子集包含的特征数;α、η分别表示等式右边两项的权重,依据文献[13]对α、η的设置推荐值,设α=0.99、η=0.01。
4.3 实验结果分析
如图8所示为MRFS算法对混合特征集的初步筛选阶段中序列特征子集的识别率曲线,说明了不同容量的特征子集输入到分类器中表现出各自不同的识别率。当以总序列特征的前18个特征作为分类器输入的预选特征子集时,识别率达到78.64%的峰值,其对应特征与排序分别为:方根幅值、频率方差、E36、λ27、λ24、PF1、λ25、PF2、λ26、PF3、λ29、λ23、E37、IMF1、IMF6、λ22、重心频率、λ11。对应特征序号如表5所示,MRFS对轴承各状态的识别率如表6所示。
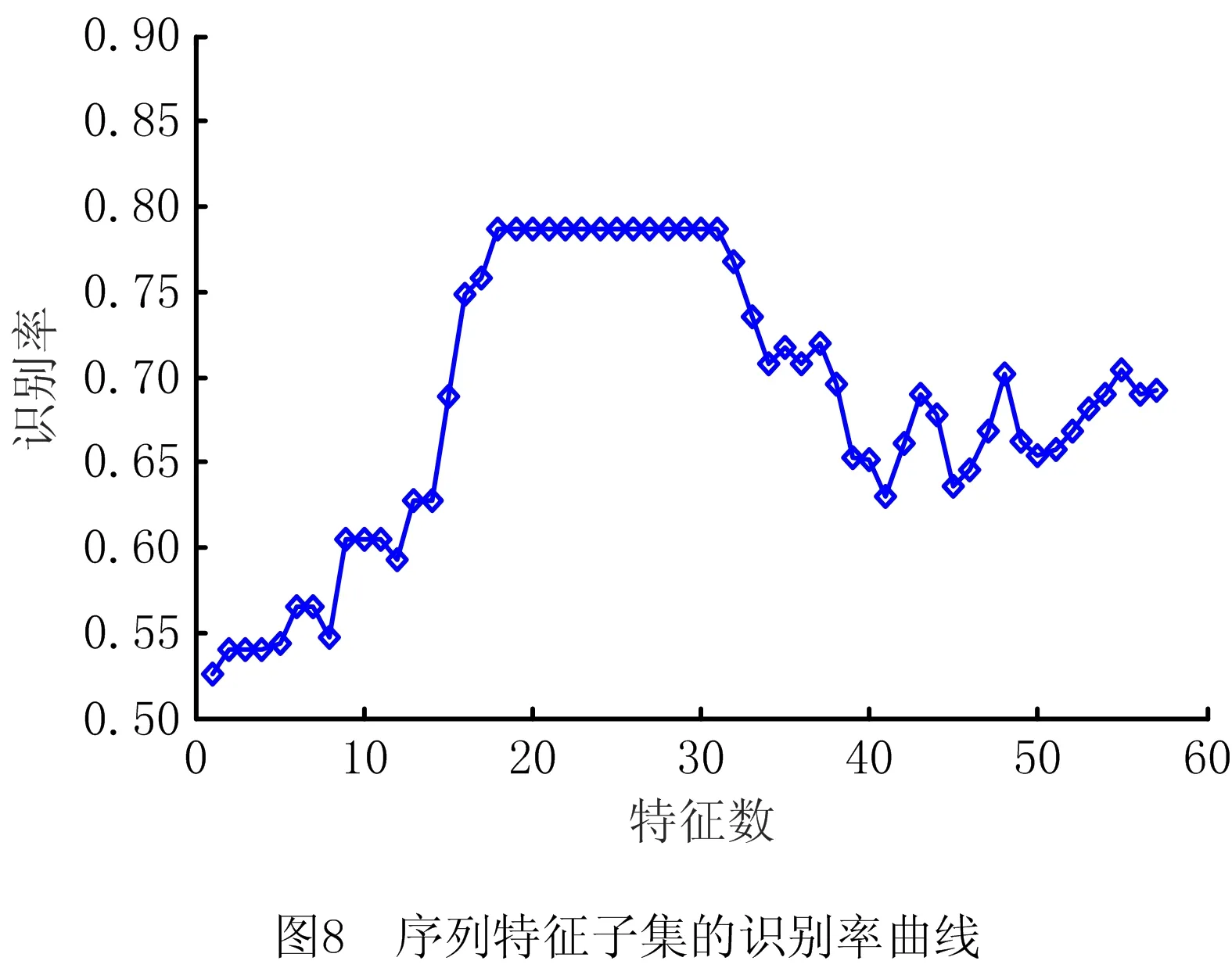

表5 预选特征子集的特征序号

表6 MRFS对轴承4种状态的识别率 %
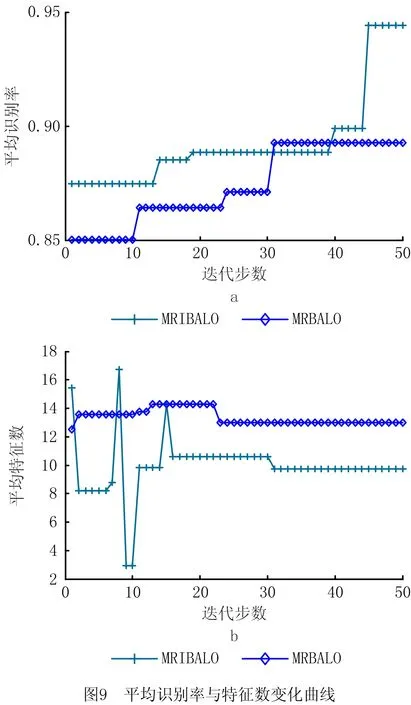
由于Filter式的MRFS算法是与MRBALO、MRIBALO共有的特征选择流程,该特征子集Sf亦作为MRBALO与MRIBALO在Wrapper特征选择中的共同输入。如图9所示为MRBALO与MRIBALO在Wrapper特征选择过程中经20次独立求解的平均识别率γR与特征数N随迭代步数变化的曲线。可以看出,在在迭代过程中,除个别点外,MRIBALO平均识别率整体上高于MRBALO,且平均特征数小于MRBALO,说明本文提出的MRIBALO特征选择算法既提升了识别率,在特征约简方面也有所成效。
为了更直观地对算法性能作出比较,表7列出了本文算法MRIBALO和MRBALO算法识别率与特征维数的具体数据,包含平均识别率最高的最优组与20次实验各组的识别率均值与特征维数均值。结合表6可以看出,由MRFS得到的正常状态与内圈故障识别率分别为56.24%、69.11%,特征子集维数为18;而表7中基于ALO的混合式特征选择算法对故障的识别率均超过80%,特征子集维数小于13。由此看出,基于ALO的混合式特征选择算法有效地对轴承故障分类精度及特征维数进行了优化,其中以MRIBALO表现最优,最优组识别率相较于MRBALO提升了3.64%,最优组特征约简比例为18.18%;平均识别率相较于MRFS与MRBALO分别提升了15.67%、5.15%,平均特征约简比例分别为45.94%、25.03%,证明了MRIBALO特征选择模型在提升滚动轴承故障的识别率与缩减故障特征维数方面的优越性。
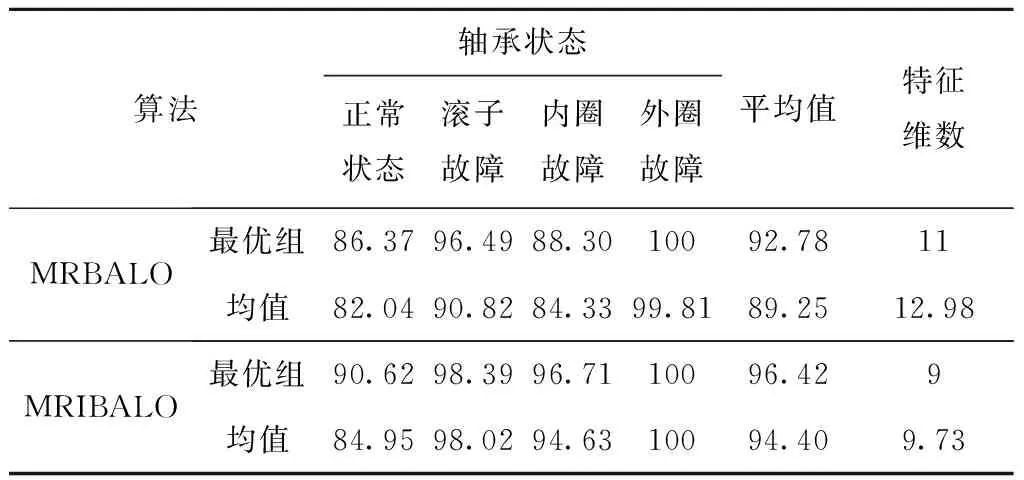
表7 识别率(%)与特征子集维数对比
5 结束语
本文针对传统二进制蚁狮算法在离散空间内对最优特征子集的寻优能力不足的缺点,提出一种基于种群保护集和多种群策略的二进制改进算法,并将该算法融入混合式特征选择算法中,实现了滚动轴承故障集的特征优化选择,主要结论如下:
(1)将本文提出的改进二进制蚁狮算法IBALO与MRMR结合形成一种新型混合式特征选择算法模型MRIBALO,并在UCI标准测试数据集与滚动轴承故障数据集上分别应用该模型,结果表明,MRIBALO模型的识别精度与特征约简能力明显优于MRFS与MRBALO。
(2)本文提出的MRIBALO特征选择模型质量优越的原因在于:IBALO中引入了种群保护集策略与并行迭代策略,使蚂蚁群体中具有寻优潜力的个体有机会进入保护集内,维持种群多样性,提升算法的收敛速度和全局收敛性能。
本文通过仿真模型测试了改进的二进制蚁狮算法IBALO算法性能,下一步需要采用马尔科夫模型、鞅理论等数学方法对蚁狮算法以及改进蚁狮算法进行理论推导,全面研究算法的收敛性能。
