基于仿真评价方法的适应性合作换线策略
2021-08-12王奕祺张晓冬
王奕祺,张晓冬
(北京科技大学 东凌经济管理学院,北京 100083)
0 引言
随着市场竞争日益激烈,为了满足消费者的多样化需求,制造业企业纷纷将传统的大规模批量生产方式转变为多品种小批量的生产方式。然而,生产方式的转变也导致了生产线切换(换线)操作的频繁发生。据研究显示,换线时间对生产率、交货期、在制品库存和质量均产生显著影响[1]。
换线作为生产过程中的重要环节,是指将一条生产线中的机器从生产一种产品转换为另一种产品的过程,涉及程序编写、调试和检验等复杂知识处理作业。由于换线操作的复杂度高且任务易于分解,在生产中常常通过多名生产者合作换线的方式来缩短换线时间。可以说,换线操作需要生产系统中的人机以及人人协同完成。然而,当前学术研究对于换线操作的优化思路主要集中于对SMED(single minute exchange of die)工具[2]的应用和发展[3-5]以及优化作业排序[6-8],缺乏对于生产者合作换线方式的关注。
由于合作生产方式可以使一项工作的至少一部分任务被同时执行,使得该方式常常作为一种组织驱动因素用于改善生产效率等性能[9]。此外,QIN等[10]将合作看作提升人员柔性的一种方式,可用于提升生产系统对于波动制造环境的适应能力。一些文献对考虑生产者合作的静态调度问题进行了研究。BUZACOTT[11]使用排队模型分析了合作型团队的绩效,发现该团队的平均任务完成时间少于个人独立完成任务的时间;WANG等[12]提出一种考虑生产者合作的柔性生产车间人员调度模型,实验结果表明与不考虑合作的模型相比,合作模型可以将生产力集中于关键任务上,以此缩短完工时间、降低最大的生产者负荷;CELANO等[13]提出一种允许上下游人员互助的U型装配线人员调度模型,目标是输送机的总停机时间最小,通过遗传算法对采用不同帮助策略的模型进行求解并对比结果,得到了不同工作站长度和工人移动速度的情况下生产系统所应采取的最优策略。
静态调度模型假设生产系统中的事件是可预测和确定性的,是一种对实际生产过程的简化描述。相比静态调度,动态调度可以根据系统的实时生产状态进行反应性调度,使其得到的调度方案更具操作性[14]。动态调度的实现方式有实时调度和静态方案的重调度两种。实时调度模型考虑了生产系统中的随机性,可以更加准确地描述实际生产过程。在考虑合作的实时调度模型中,生产者所采取的合作策略会对调度结果产生重要影响。当前一些学者利用动态仿真分析方法对生产者合作策略进行了研究。其中,邱君降等[15]对生产系统中维修人员所采取的独立维修策略和合作维修策略进行对比仿真研究,结果表明采取合作策略对系统中的设备运转率、维修员利用率、运转率波动度和维修薪酬均产生显著优化;曹阳华等[16]对U形混流装配线中生产者合作对生产系统的影响进行了仿真研究,仿真结果表明当生产压力较大时,采取合作策略的同时优化工作优先序相比采取不合作策略,能有效地提高生产效率和任务均衡率;张晓冬等[17]基于组织学习效应,对生产单元中生产者在选择合作伙伴时所采取的指定合作策略和自主合作策略进行对比仿真研究,结果表明采取自主合作策略时所得到的任务完成时间、人员利用率、合作学习效应等评价指标均存在显著优势;ZHANG等[18]依据不同的合作程度提出4个合作换线策略,并在不同的制造环境下开展各个策略的对比仿真研究,明确了合作行为的适用范围。上述文献对生产中是否采用合作策略以及采用何种合作策略进行了有益探索,同时也说明了仿真分析方法的有效性。但是,这些研究所设计的合作策略均基于固定规则,使得策略对于系统性能的优化程度有限,且缺乏对于不同生产环境的适应能力。
鉴于以上文献存在的不足,本文对基于仿真评价方法的适应性合作换线策略进行研究,旨在使生产者所持有的策略具备更强的优越性和对生产环境的适应性。适应性策略的思想是通过对生产者所持有的策略进行编码、设置初始策略和策略迭代过程的方式,使每代生产过程仿真模型中的生产者持有不同的策略,并最终输出最优或满意策略。
1 问题描述
1.1 换线操作过程
本节介绍生产者独立换线和合作换线的操作过程,及两种换线方式所需工时消耗的计算公式,所研究的合作换线行为限定为2人合作。为方便描述,定义在生产过程中领取到换线任务的生产者为k1,生产者k1根据所持合作策略可确定进行独立换线或与生产者k2进行合作换线。依据文献[18]和现场调研结果,得到了生产者独立换线和合作换线的操作过程,如图1所示。由图1可知,合作换线过程按照两名生产者合作方式的不同可以划分为并行换线阶段和协作换线阶段两个阶段。

在并行换线阶段中,生产者k1需要执行的操作包括导入新程序或调用原程序、检查程序和定位基准(将该部分操作定义为s1);生产者k2需要执行的操作包括拆卸和清洗原工装夹具、清洗安装台、安装新的工装夹具(将该部分操作定义为s2)。该阶段通过将整体操作进行分解,并按照任务量较为均衡地分配给两名生产者独立完成的方式,将串行工作流程转化为并行工作流程。
在协作换线阶段中,两名生产者通过配合,产生了协作效应,共同完成调试和记录结果的操作(将该部分操作定义为c),缩短了换线时长。
由上述两种换线方式的过程,可分别得到所需工时的计算公式。生产者k1独立换线所产生工时消耗Tk1的计算公式如式(1)所示:
(1)

生产者k1和k2合作换线所产生工时消耗Tk1k2的计算公式如式(2)所示:
k1=1,2,…,K;k2=1,2,…,K;k1≠k2。
(2)
式中tck1k2为生产者k1和k2协作完成操作c的工时消耗。
1.2 适应性合作换线策略的提出
生产系统的生产计划下达之后,需要为每名生产者指定合作换线策略。生产者在领取到某产品在某台机器上的换线任务后,可根据所持合作换线策略和与其他生产者的交互结果,进行独立换线或与某生产者合作换线的决策。本文将完成生产计划所需的生产周期作为评价指标,用于衡量合作换线策略的优越性。
1.2.1 基于规则的合作换线策略
当前研究均要求生产系统的管理者为生产团队指定某种基于规则的合作换线策略,即每名生产者持有相同的策略。
生产团队关于采取独立或合作的换线方式存在两种常见策略:独立优先策略和合作优先策略。独立优先策略是指生产者k1不发起合作而直接选择独立换线;合作优先策略是指生产者k1向其他所有生产者发送合作任务,如果申请者不少于1人,则生产者k1根据协调规则确定唯一的合作者k2并与其开始合作换线,当无申请者时,生产者k1选择独立换线。
此外,随着当前市场竞争的加剧,越来越多的生产企业针对市场需求快速推出具有新技术、新功能和新工艺的产品,从而抢占先机、赢得竞争[19]。新产品相对成熟产品而言,由于生产者对产品任务没有足够的经验积累,造成任务的工时消耗显著增加,特别是与生产工艺密切相关的换线任务。因此,产品的类型(新产品或成熟产品)也应是合作换线策略需要考虑的因素之一,新产品可指代相同类型或产品族中工时消耗较高的产品。从这一角度出发,将两类产品与两种策略进行组合可生成4种基于规则的合作换线策略:完全不合作策略、成熟产品合作策略、新产品合作策略和完全合作策略。表1对4种策略进行了详细描述。

表1 4种基于规则的合作换线策略及描述
可以看出,基于规则的合作换线策略存在如下不足:①由于策略分类的精细化程度较低,导致可选择策略的总数过少;②策略无法保证对不同的生产环境(生产计划、生产团队等因素构成)具有适应性;③生产系统的管理者缺乏一种有效机制,使其可根据每名生产者自身技能和环境等因素合理地进行策略指定。
1.2.2 适应性合作换线策略的特点
根据上述基于规则的合作换线策略的不足,本文拟提出一种适应性合作换线策略,并构造出若干个典型的生产环境,使适应性策略应用于各生产环境时均可优于基于规则的策略。适应性合作换线策略应具有如下特点:
(1)对生产者领取到换线任务时的情况进行细分,可通过对3类生产状态的变量(机器编号、产品类别、其他生产者对合作换线任务的反馈)进行组合得到所有的情况。进一步设计一种适应性合作换线策略的编码方式,使其可为生产者在每一种情况下的决策提供支持。
(2)将生产计划、工艺信息、设施布局信息、生产团队信息作为生产环境的组成要素,设计一个适应性合作换线策略的迭代过程,使其可为任一生产环境中的每名生产者输出符合编码规则的满意策略。
2 基于仿真的适应性合作换线策略
本章将对适应性合作换线策略的编码方式和迭代过程进行具体介绍。
2.1 编码方式

2.2 迭代过程
所提出的适应性合作换线策略基于模拟退火(Simulated Annealing, SA)算法的思想,并将生产过程的仿真用于对当前策略的评价过程,迭代过程如图2所示。

SA算法是基于固体物质的退火过程与一般组合优化问题之间的相似性所提出的一种全局优化算法[20]。算法需要对初始参数进行设定,包括初始温度T0、结束温度Tend、降温速率q和链长L。
生成初始解的方法设置如下:首先对生产者分别采用4种基于规则的策略的生产过程进行仿真和评价;其次将这4种策略中的最优策略设置为初始解S2。
在迭代过程中,Metropolis准则是使算法跳出局部最优区域,并收敛于全局最优解的关键设置[21],如式(3)所示:
(3)
式中:P为将当前解S2赋值给S1的概率;T为当前温度;f(S1)和f(S2)分别为对策略解S1和S2的评价值。可以看出,在前期迭代过程中,S1会以较大概率接受劣解;而随着温度降低,S1接受劣解的概率逐渐变小。
生成邻域解的方法设置如下:随机选择1~2名生产者,并继续在被选择生产者的策略解中随机选择1~2个位置进行位值更改。
对于当前解S2的评价过程是迭代过程中最为复杂和关键的环节。由于生产过程中包含大量的随机性、离散事件和非线性关系,生产者具有主动性和协作性,导致无法利用数学模型对上述特征进行准确描述[22]。这种情况下,仿真被认为是最有效的研究方法。基于此,本文构建了生产过程仿真模型,并通过对生产过程的仿真实现对当前解S2的评价。考虑到动态仿真分析方法具有随机性,本文设置对输入为S2时的模型独立且重复地仿真运行n次,并将n次仿真所得生产周期的均值作为f(S2)。下面将继续对生产过程模型的结构、仿真运行逻辑和agent模型的构建方法进行介绍。
3 生产过程仿真模型
3.1 模型结构
生产过程模型的结构如图3所示,由多agent模型、离散生产模型和人机协同接口3部分组成。
(1)多agent模型由一个管理者agent、生产者agent群体和一定数量的机器agent组成。机器agent可通过事件触发机制检测工件的加工状态,并将生产状态数据通过人机协同接口发送至管理者agent以及与生产者agent协同生产。管理者agent可以向生产者agent群体集中发布生产任务,并根据群体的反馈信息完成对生产任务的分配。单个生产者agent可以进行分布式决策和生产操作;两个生产者agent可以进行合作。
(2)离散生产模型的构建共分两步:首先收集生产系统的相关信息,如生产计划、布局信息和产品工艺信息等;其次根据所收集的信息利用离散事件建模方法和机器agent构建模型。
(3)人机协同接口用于实现生产者agent和机器agent的协同生产过程,一方面将机器agent生成的生产状态数据传递至管理者agent,另一方面驱动生产者agent参与离散生产过程。人机协同接口的提法可以使人机集成生产过程模型的结构更加清晰,其实现方法需要通过对管理者agent、生产者agent和机器agent之间交互功能的开发。

3.2 仿真运行逻辑
在初始化生产计划和生产者的合作换线策略S2等信息后,离散生产模型将作为生产过程模型的运行主线。仿真模型的运行逻辑如下(后文中的生产者agent、机器agent和管理者agent分别简称为生产者、机器和管理者):
(1)离散生产模型首先被启动,当运行至机器检测到产生需要生产者参与的操作时,机器将通过人机协同接口把生产状态数据传递给管理者。
(2)管理者收到生产状态数据后进入生产任务分配阶段,本阶段中agent之间的交互服从合同网协议(contract network protocol)[23]。管理者根据数据生成相应的生产任务,并将任务向生产者群体发布。群体中每个生产者接收任务信息后进行判断,如果自身状态为“空闲”且具备所需技能,则向管理者反馈“同意”;否则反馈“拒绝”。当反馈“同意”信息的生产者数量不少于1时,管理者按照协调规则向1名生产者发送任务确认信息;否则,管理者将该任务添加至待分配任务列表,等待执行完生产操作的生产者主动选取。
(3)生产者领取任务后进入生产方式确定阶段。领取到任务的生产者向其他生产者发布合作任务,接收到合作任务信息的生产者所采用的反馈规则同上一阶段。收到反馈信息后,生产者再结合任务信息和合作策略S2可确定独立或合作的生产方式。如果是合作生产方式,该生产者会向合作者发送确认信息。
(4)人机协同接口根据生产者的行为输出数据驱动1名(独立生产方式)或2名(合作生产方式)生产者参与生产过程。
(5)重复(1)~(4)直至完成生产计划后,仿真运行终止。通过仿真钟所记录的本次生产过程的起止时间可计算得到生产周期,并将其作为对合作策略S2的单次评价。
3.3 agent模型的构建方法
本节介绍生产过程模型中复杂度最高的agent模型的构建方法。其中,生产者agent模型采用文献[24]所提出的基于状态图(statechart)的方法完成构建,不再赘述。考虑到仿真软件Anylogic支持采用离散事件和agent的混合方法进行建模,并且内置了丰富的插件库以及agent的通信、移动等方法,本文选择该软件构建生产过程模型,并利用Java语言进行二次开发。
3.3.1 机器agent模型的构建方法
机器检测工件的加工状态以及与生产者协同生产的过程均可看作由离散事件所驱动的。依据该思路,可以利用Anylogic软件中内置的流程建模库完成对机器agent模型的构建,其内部离散事件模型如图4所示。
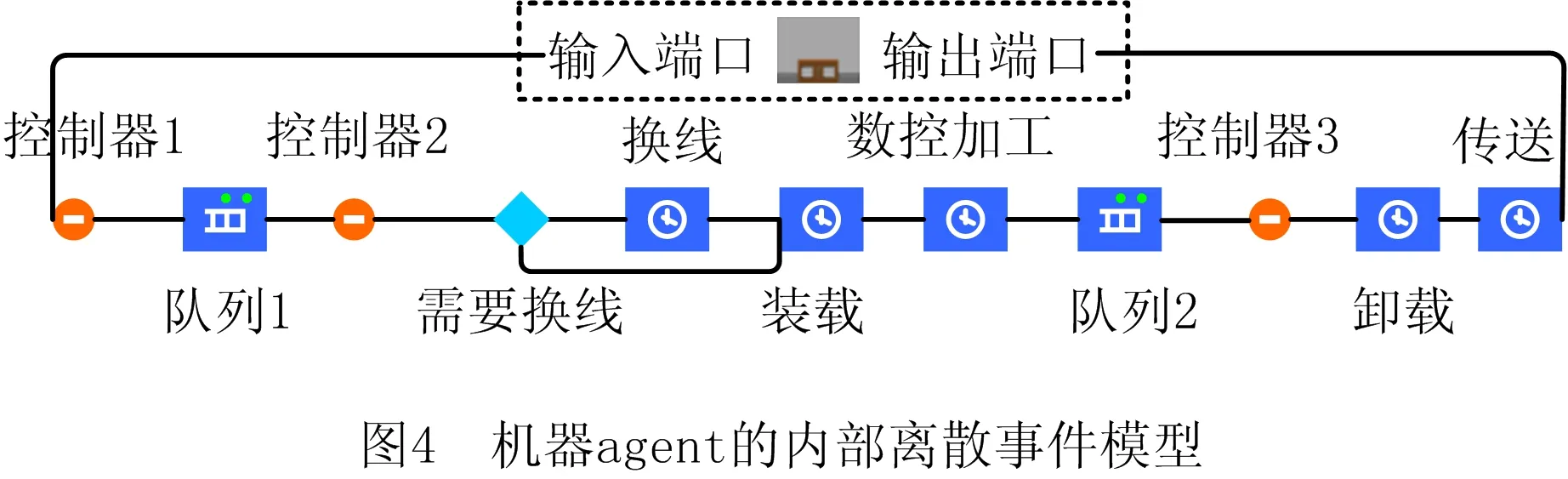
本段结合图4描述工件流经机器的过程。
(1)分别设置“控制器1”和“控制器2”的初始状态为“不阻止”和“阻止”,则工件从输入端口流入机器后,会通过“控制器1”并停留在“队列1”中。并且令“控制器1”在有工件进入时,将自身状态更改为“阻止”。
(2)当工件进入“队列1”时,机器通过工件型号判断是否需要换线。如果需要,则机器向管理者发送“等待换线操作”的生产状态信息;否则发送“等待装载操作”的生产状态信息。
(3)管理者收到信息后,依次完成生产任务分配阶段和生产方式确定阶段。
(4)当领取任务的生产者移动至机器处时,将“控制器2”的状态更改为“不阻止”。并且令“控制器2”在有工件进入时,将自身状态更改为“阻止”。
(5)如果机器不需要换线操作,则工件直接进入“装载”组件进行延迟;否则,工件依次进入“换线”组件和“装载”组件进行延迟。
(6)生产者在完成装载任务后结束工件在“装载”组件中的延迟。随后,工件进入“数控加工”组件延迟指定的时间。
(7)设置“控制器3”的初始状态为“阻止”,因此工件在离开“数控加工”组件后会停留在“队列2”中。当工件进入“队列2”时,机器向管理者发送“等待卸载操作”的生产状态信息。
(8)与(3)同理,依次完成上述两个阶段。
(9)当领取卸载任务的生产者移动至机器处时,将“控制器3”的状态更改为“不阻止”。并且令“控制器3”在有工件进入时,将自身状态更改为“阻止”。工件离开“控制器3”后进入“卸载”组件进行延迟,直至生产者完成卸载任务。
(10)工件离开“卸载”组件后进入“传送”组件。并且令“传送”组件在有工件进入时,将“控制器1”的状态更改为“不阻止”。工件延迟指定的传送时间后,从输出端口流出机器。
3.3.2 管理者agent模型的构建方法
本文利用状态图和动态事件描述管理者接收不同信息后的行动设置,如图5所示。其中,状态图包含一个“等待信息”状态和两个状态内的变迁。

管理者收到来自机器发送的生产状态信息后,发生变迁并产生如下3个行动:①根据信息生成相应类型的生产任务;②将任务添加至待申请任务列表,并将任务发布至生产者群体;③在任务申请截止期到达时,生成该任务的“生产者指派”动态事件。
管理者收到来自生产者发送的任务申请信息后,发生变迁并将生产者添加至该任务的申请者列表中。
4 案例研究
本文将所提出的适应性合作换线策略应用于某机加零部件生产单元。该生产单元配备了18台数控机床(编号M1~M18)、6名生产人员(编号W1~W6)和自动化传送装置等。该单元主要生产3个类型的零件,编号分别为BXT、FGT和FXT。单元内的订单批量较小、需求多变,时常引入新型零件,采用多品种、小批量的混流生产模式。该单元目前采用基于规则的合作换线策略,且订单交货期压力较大,因此迫切需要通过为生产人员指定更优的合作换线策略来缩短生产周期。
4.1 生产单元基本信息
在本案例中,生产人员需在机床加工零件前对零件完成安装操作,在加工后完成拆卸操作,与图4中的描述相对应。此外,当生产单元进行不同类型的零件切换或引入新零件订单时,生产人员需要根据零件的工艺特点对相应的机床进行换线操作。零件的装卸时间和换线时间均服从正态分布,数控加工时间为恒定值。同类型机床的装卸技能是通用的,而同类型机床的换线技能还和零件的工艺有关。仿真模型中的假设和规则如表2所示。

表2 仿真模型中的假设和规则
由表2可知,零件BXT和FGT可以同时加工,而零件FXT由于工艺路线中的机床约束只能单独加工。该生产单元仿真模型的3D示意图如图6所示。

表3给出了3类零件在工艺路线上的数控加工时间,表4所示为该生产单元的人员技能配置方案。每名生产人员掌握2个技能水平不等的装卸技能和2个技能水平相等的协助换线技能,生产人员W2、W3和W4掌握特定机床的独立换线技能。具有协助换线技能的生产人员可与具有独立换线技能的生产人员合作换线,但不具备独立换线能力。表4中:OSa(d1)代表对Sa类装卸技能具有d1级水平,CMb(d2)代表对机床Mb的独立换线技能具有d2级水平,AMc(d3)代表对机床Mc的协助换线技能具有d3级水平。

表3 3类零件的数控加工时间 s

续表3

表4 人员技能配置方案
表4中生产人员的换线技能均适用于成熟零件和新零件,但两类零件所需的工时消耗具有差异。表5所示技能等级为5的生产人员对6台机床换线所需工时的分布,表中第一组数据为成熟零件换线操作所需时间的均值和标准差,第二组数据为新零件换线操作所需时间的均值和标准差。技能等级从1~9逐渐增高,相邻等级的完成时间均值相差5%。为方便实验设计,假定同一类型的新零件和成熟零件的工艺路线相同。

表5 换线操作独立完成的时间分布 min
如表6所示为具备独立换线技能的生产人员与具备不同协助换线技能水平的生产人员合作完成6台机床的换线操作c时的工时分布。

表6 换线操作c的合作完成时间分布 min
4.2 实验设计
取28个订单构成订单序列,并设置4个不同的新零件引入率:0、25%、50%和75%,用于考察合作换线策略对生产环境的适应能力。实验设计方案如下:使生产人员分别采取5种合作换线策略(适应性策略和4种基于规则的策略),在4个生产环境下进行对比仿真。如表7所示为模拟退火算法的参数设置,对于基于规则的策略在每个生产环境下的仿真次数也取20次。

表7 模拟退火算法参数设置
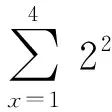
每种情况所对应策略编码中位置y的计算公式为:
(4)
式中:z1取0和1分别对应2个机床编号;z2取0和1分别对应成熟零件和新零件;z3取0和1分别对应第1名潜在合作人员的反馈信息为“同意”和“拒绝”;z4取0和1分别对应第2名潜在合作人员的反馈信息为“同意”和“拒绝”。例如,生产人员W2的合作换线策略编码为110100101110,W2需要对机床M3进行BXT类型新零件的换线操作,生产人员W1和W3均对该合作换线任务均反馈“同意”。假设对于生产人员W2,定义z1取0和1分别对应机床M3和M4,生产人员W1和W3分别对应第1名和第2名潜在合作人员。那么可通过式(4)计算y值为3,由于策略编码的第3位为0,所以生产人员W2进行独立换线。
4.3 结果与讨论
采用5种合作换线策略在4个生产环境下所得的生产周期均值对比如图7所示,为了更加直观地反映不同实验方案之间的差异,图中数据为剔除下班时间后的有效生产周期。由图7可知,随着新零件引入率的提升,采用每种合作换线策略所得生产周期均表现出增大的趋势,这是由于新零件的任务需要更多工时消耗导致的。此外,采用适应性策略所得生产周期在所有的生产环境下均优于采用其他4种策略。

为验证采用适应性策略与其他4种策略在每个环境下所得生产周期均值是否存在显著性差异,对图7中的数据进行了单因素方差分析。在新零件引入率为25%的环境下,分析结果显示数据不满足方差齐性,进一步采用Games-howell方法进行比较分析;在其他3个环境下,分析结果显示数据满足方差齐性,进一步采用LSD方法进行比较分析。4个环境下采用适应性和基于规则的合作策略所得生产周期均值的单因素方差分析结果如表8所示。表8中,合作策略号1~5分别对应完全不合作策略、成熟产品合作策略、新产品合作策略、完全合作策略和适应性策略。分析结果显示,采用适应性策略相比4种基于规则的策略在所有的生产环境下均具有显著性优势,一方面说明了适应性合作策略用于优化系统性能的优越性,另一方面也表现出适应性策略对不同制造环境的适应能力。
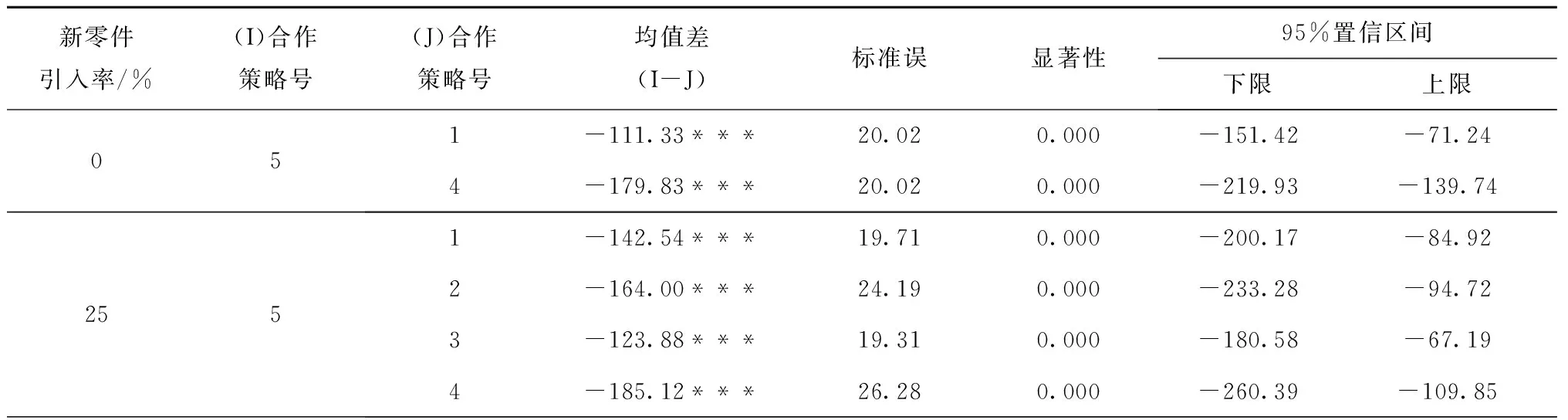
表8 4个环境下采用适应性和基于规则的合作策略所得生产周期均值的单因素方差分析结果

续表8
出现上述实验结果的原因有以下4点:
(1)适应性策略的编码方式极大地丰富了合作策略的解集,使得生产人员更加充分地利用生产信息,而每种基于规则的合作策略只是解集中的1个解。在本案例中,适应性策略的解集中包含的策略总数为236。
(2)模拟退火算法的迭代过程保证了最终输出的满意策略具有较高质量。以新零件引入率为50%的生产环境为例,适应性策略的迭代过程如图8所示。适应性策略以新产品合作策略作为初始解,在迭代的初始阶段以较大的概率接受劣解,从而有效避免陷入局部最优。随着迭代次数的增加,算法接受劣解的概率随着降低,最终在第569次迭代时收敛于具有较高质量的满意解。
(3)相比基于规则的合作策略,适应性策略可使每个生产人员根据自身技能配置和生产计划等因素持有不同的合作策略,使得生产人员更加合理地利用生产信息。再以新零件引入率为50%的生产环境为例,生产人员W2、W3和W5的初始策略均为001100110011(新产品合作策略),而经过迭代优化后的策略分别为101100001100、101000001111和110111001100。

(4)相比基于规则的合作策略,适应性策略可使同一生产人员随着生产环境的改变调整其所持有的合作策略,从而提升生产系统适应不同生产环境的能力。以生产人员W2为例,其在新零件引入率为0、25%、50%和75%的环境下,输出的满意策略分别为001110101001、000000100000、101100001100和110010101010。
5 结束语
多品种、小批量生产方式下的换线操作频繁发生,本文提出一种基于仿真评价方法的适应性合作换线策略用于指导生产者进行换线方式和合作者的选择,从而缩短完成生产计划的周期。所提出的适应性策略的特点是以模拟退火算法流程进行迭代,以生产过程的仿真结果对当前策略进行评价。以研究案例为背景,通过仿真软件分别对4种典型生产环境下,生产者采用适应性策略和基于规则的策略时得到的生产周期进行模拟。实验结果表明,采用适应性策略在各种生产环境下均具有显著优势。所进行的研究也表明提出的适应性策略支持对于其他目标或多目标问题进行优化。后续研究将继续丰富生产者的合作机制,更多地发挥agent的主动性,例如丰富任务响应者的反馈策略,从而进一步提升生产系统的精细化管理水平。
