转速对并列旋转双圆柱尾流的影响研究

叶煜航，凃程旭,,3，林仁勇，葛贤福

(1.中国计量大学 计量测试工程学院，浙江 杭州 310018；2.浙江利欧泵业有限公司，浙江 温岭 317500；3.浙江大学 控制科学与工程学院，浙江 杭州 310027；4.浙江省机电集团有限公司，浙江 杭州 310002)

旋转单圆柱和静止并列双圆柱绕流作为圆柱绕流的两个典型问题，近二十年一直是该领域研究的热点，相关的研究成果非常丰富[1-5]。旋转单圆柱绕流最初引起研究人员注意的是飞行中的子弹或导弹总是绕其中心轴旋转，使其受到一个垂直于速度方向的流体作用力而偏离弹道，即马格纳斯效应(Magnus effect)[6]。后来，圆柱的旋转作为圆柱尾流控制和强制对流换热的有效方法而被广泛研究。并列圆柱的间距比是除雷诺数Re之外影响其尾流流型的又一重要因素，其中间距比T/D是两并列圆柱的中心距T与圆柱直径D的比值。随间距比的不同，静止的并列双圆柱绕流有单钝体尾流、不稳定偏流、双尾流三种基本流型[7]。目前等直径的并列旋转双圆柱绕流问题还未得到广泛关注[8-10]，至今已开展的工作主要集中于低雷诺数的数值仿真，中、高雷诺数下的则研究较少[3,11-14]。Yoon等在2007年采用浸没式边界条件下的有限体积法首次对雷诺数Re为100的并列旋转圆柱进行了数值仿真[15]。2008年Yoon等又对该问题进行了进一步研究，探讨了并列旋转双圆柱绕流场的频率特性及压力分布特性[16]。同年末，郭晓辉等同时利用PIV技术和浸没式的格子玻尔兹曼方法(LBM)对中等雷诺数(Re=425～1 130)并列旋转双圆柱绕流问题的进行了实验研究和数值仿真，发现并列旋转双圆柱的尾涡控制机理与单旋转圆柱绕流有很大不同[17]。2014年凃程旭等采用PIV技术研究了不同间距比T/D下并列旋转双圆柱的尾涡控制机理[8]。本文将并列圆柱的旋转方向归纳为3种类型(见图1)，同时采用PIV技术和热线风速仪对不同旋转速度下并列旋转双圆柱绕流场的流动特性进行实验研究。

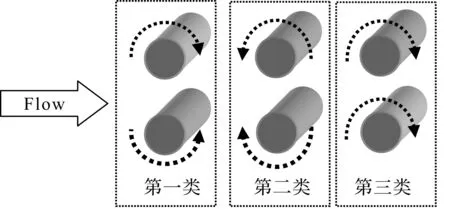
图1 双圆柱的3种旋转类型[8]Figure 1 Rotational direction[8]

1 实验设备和方案

本实验对Re为950、间距比T/D为1.6的并列旋转双圆柱绕流场进行了研究，是在中国计量大学的回流式循环风洞中开展的，利用PIV系统和热线风速仪分别采集瞬态整场速度分布和单点高频速度信号。风洞实验段长2 m，截面尺寸为600 mm×600 mm，由透明有机玻璃镶嵌于钢框架内封闭而成。实验所用圆柱为两根等直径(25 mm)的铝合金圆棒，其两侧通过轴承水平支撑于风洞侧壁。两圆柱各由一个电机通过齿轮驱动。实验模型的阻塞比远小于1.0，圆柱的长细比大于20，故忽略风洞壁面和圆柱端部对流场的影响，近似将本文的并列旋转双圆柱绕流视为二维问题。

实验采用德国Lavision公司的PIV系统，该系统由双脉冲Nd:YAG激光器、CCD相机、同步控制器及计算机系统组成。其中激光器产生532 nm的绿光，额定脉冲能量为125 mJ，激光重复率为15 Hz。CCD相机的像素达2 M(1 600×1 200 pixel)。CCD相机水平安装于圆柱轴线方向偏下游一侧，垂直于来流，通过标定得到的流向视场长度根据间距比的不同取6D～8D、视场长宽比为1.33，PIV系统和实验装置的安装见图2。示踪粒子由压力喷嘴式烟雾发生器产生，并在实验段的下游撒播，经历一定时间的充分循环后粒子浓度即可达到测量要求。判读域最小回归至32×32像素，所得矢量场的空间分辨率为毫米级。

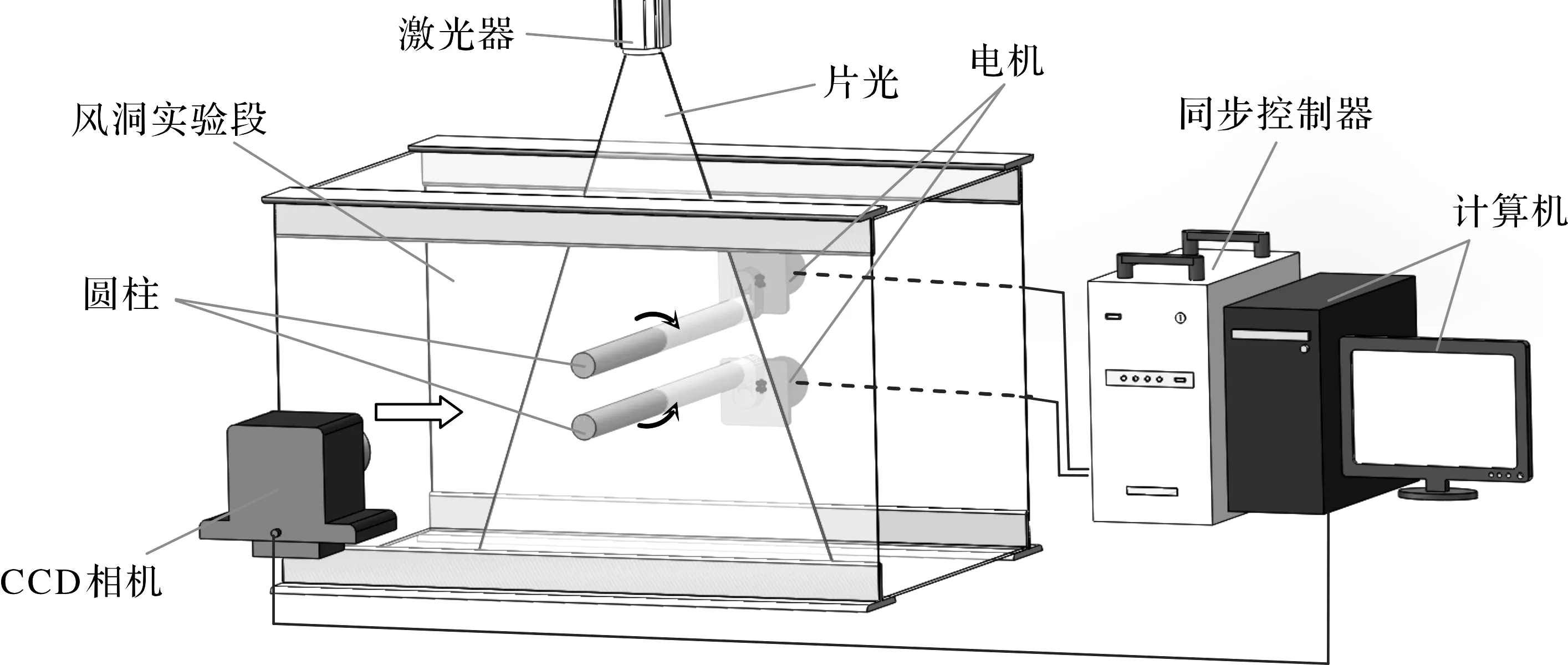
图2 PIV系统及实验装置[8]Figure 2 PIV system and experimental set[8]

热线风速仪为丹麦DANTEC公司生产的3CTA+1CCA系统，探针采用55P14一维热线探针，采样频率为1 000 Hz，每个测点上采集10 000个数据。探针固定安装在三维坐标架上，三维坐标架根据控制软件预设测量网格，带动探针进行自动定位测量，定位精度可达0.01 mm。对不同间距比采用同样的测量网格，测量网格分布参见图3。

图3 热线探针测点分布Figure 3 Distribution of the testing points

2 实验结果及分析

2.1 瞬态涡量场及分析

由瞬态涡量场对并列旋转双圆柱绕流场进行定量分析更为方便，故对PIV获取的速度矢量场进行后处理得到瞬态涡量场。需特别说明的是相对速度|α|是圆柱壁上的线速度与自由流速度的比值。本文所有的瞬态涡量场都是由无量纲化(关于圆柱直径)后的速度矢量场计算得到的，这样能够精简涡量本身繁复的数值，更直观地反映流场本身的流动特性，为避免混淆涡量的单位仍沿用s-1。

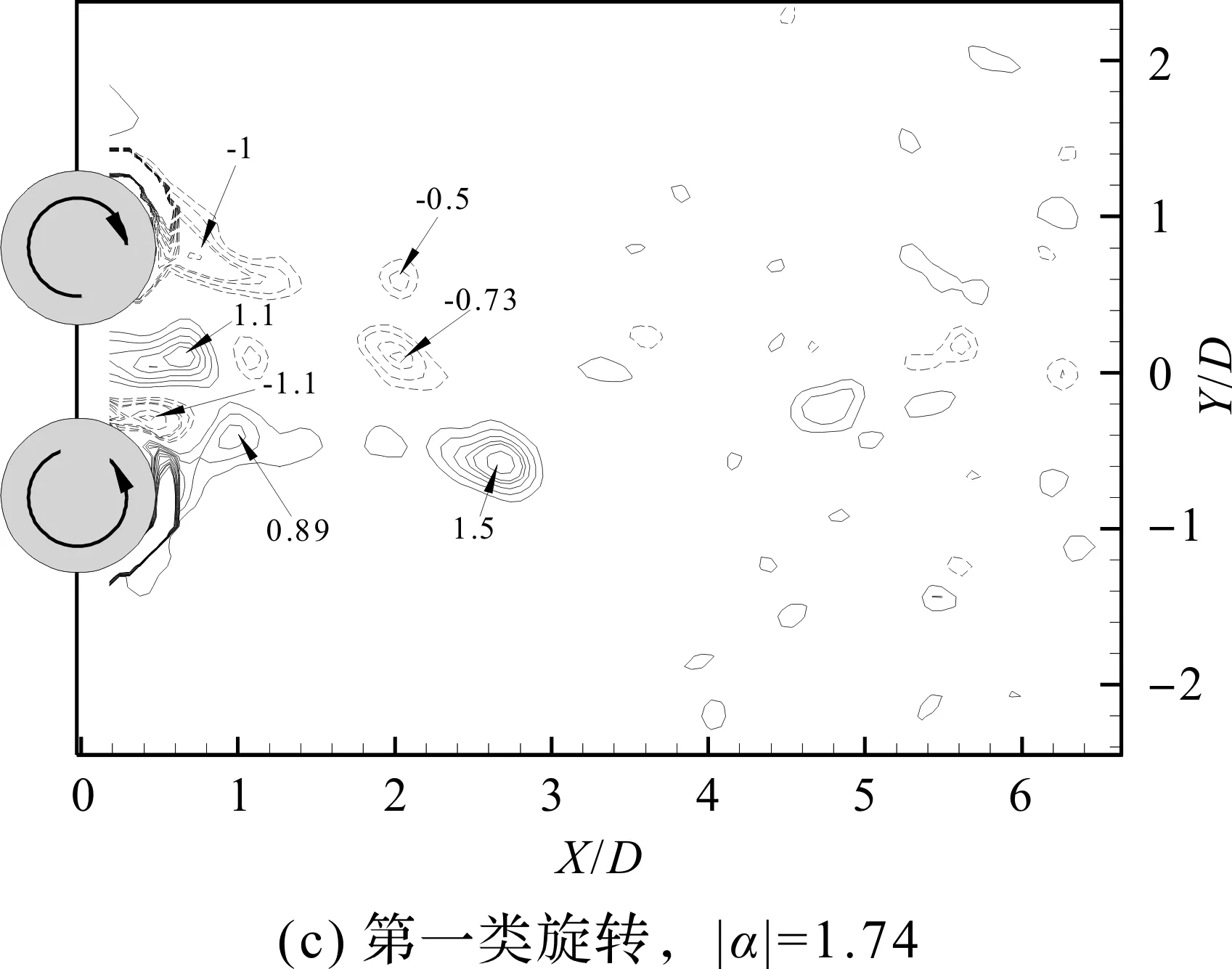
T/D=1.6，圆柱静止时，如图4(a)所示，两圆柱之间的间隙流偏向下圆柱，即不稳定偏流流型(bias-flow)，漩涡生成区域的涡量值大小在2～3之间，刚脱落的漩涡增强至3 s-1左右。当圆柱壁面的线速度接近自由流的速度时，第一类旋转中圆柱外侧的剪切层将会由两侧靠向Y/D=0，而第二类旋转类型和第三类旋转类型几乎不改变。内部剪切层发生如下显著的区别：在第一类旋转中，剪切层保持初始状态不发生显著变化；在第二类旋转中，剪切层会由初始偏流流型转化为相互平行的两对平行涡街；在第三类旋转中，自由流与偏置的间隙流之间的偏转角会增大。圆柱开始做第一类旋转后，两并列圆柱的尾迹都偏向Y/D=0，并近似关于Y/D=0对称，由偏流流型转变为双尾流流型。当|α|增加到1.31(图4(b))，偏流模式已经转化为两条平行对称的涡街，这些涡街急剧地收拢成单个涡街。涡脱落的位置由静止时的X/D=3D提前至X/D=2D，涡量强度在脱落后则迅速减小到1.5 s-1左右；随|α|增大到1.74(图4(c))，涡脱落的位置向上游移动到X/D=1D位置，漩涡分布的范围进一步缩小，涡量的大小在脱落前下降到1 s-1左右、脱落后总体有所下降但仍有大于1 s-1的漩涡存在。第一类旋转方向使得圆柱转速的变化对漩涡的强弱、大小及分布存在着显著的影响。随着|α|的逐渐增大，涡脱落的位置逐渐向双圆柱靠近，漩涡的分布范围逐渐减小。这一现象与低雷诺数下Arnab[14]，Dou[18]等人的研究结果是一致的。相比与低雷诺数下的双圆柱绕流，中等雷诺数下需要更高的圆柱转速以实现对漩涡的抑制。但当|α|从1.74增加到2.62(图4(d))，并列双圆柱的所有剪切层被压缩成一个非常狭小的区域，起初清晰的流动模式将会消失，涡量强度会增强，且分布变得更加分散。当|α|≈2.18时，对尾迹漩涡消减效果最优。

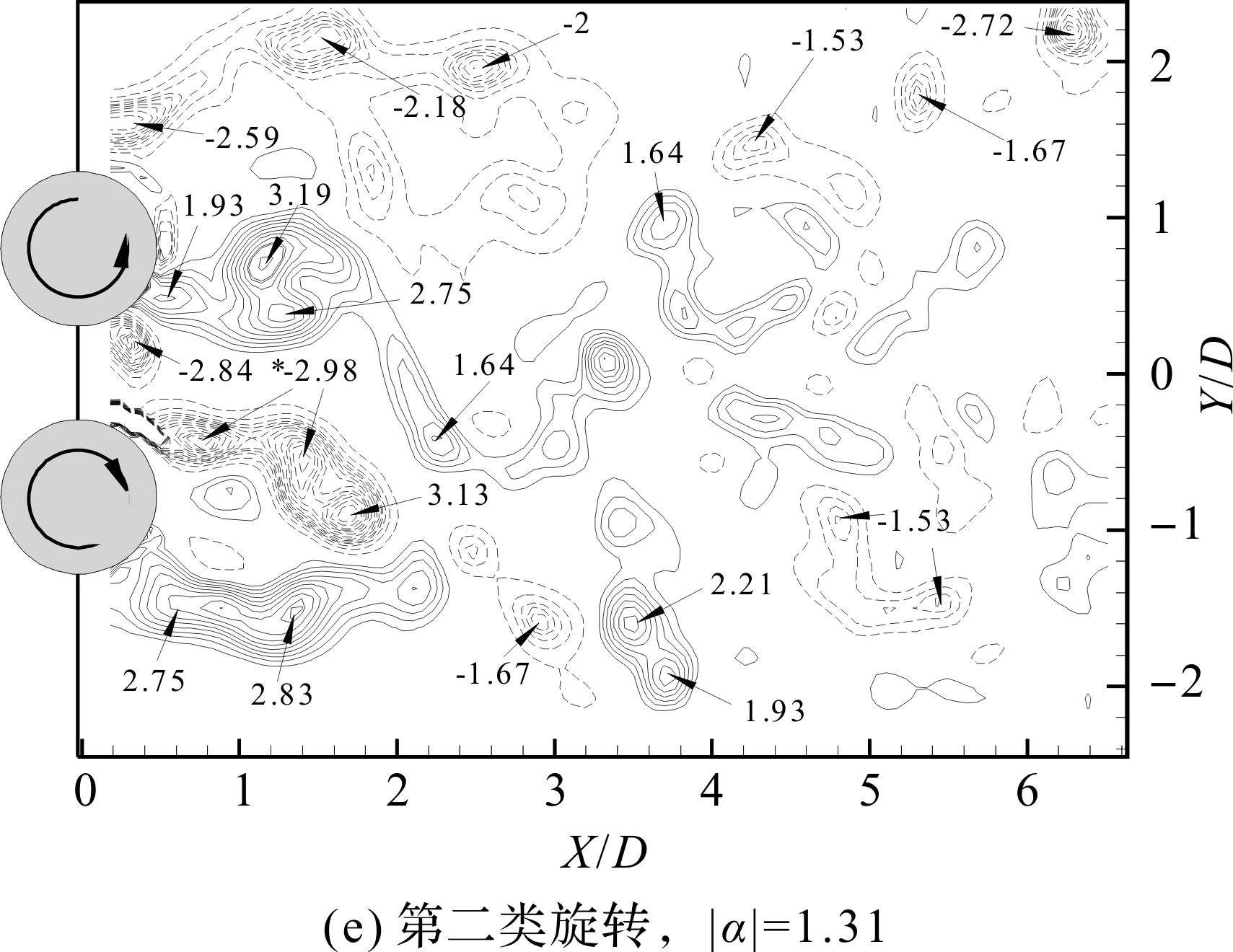
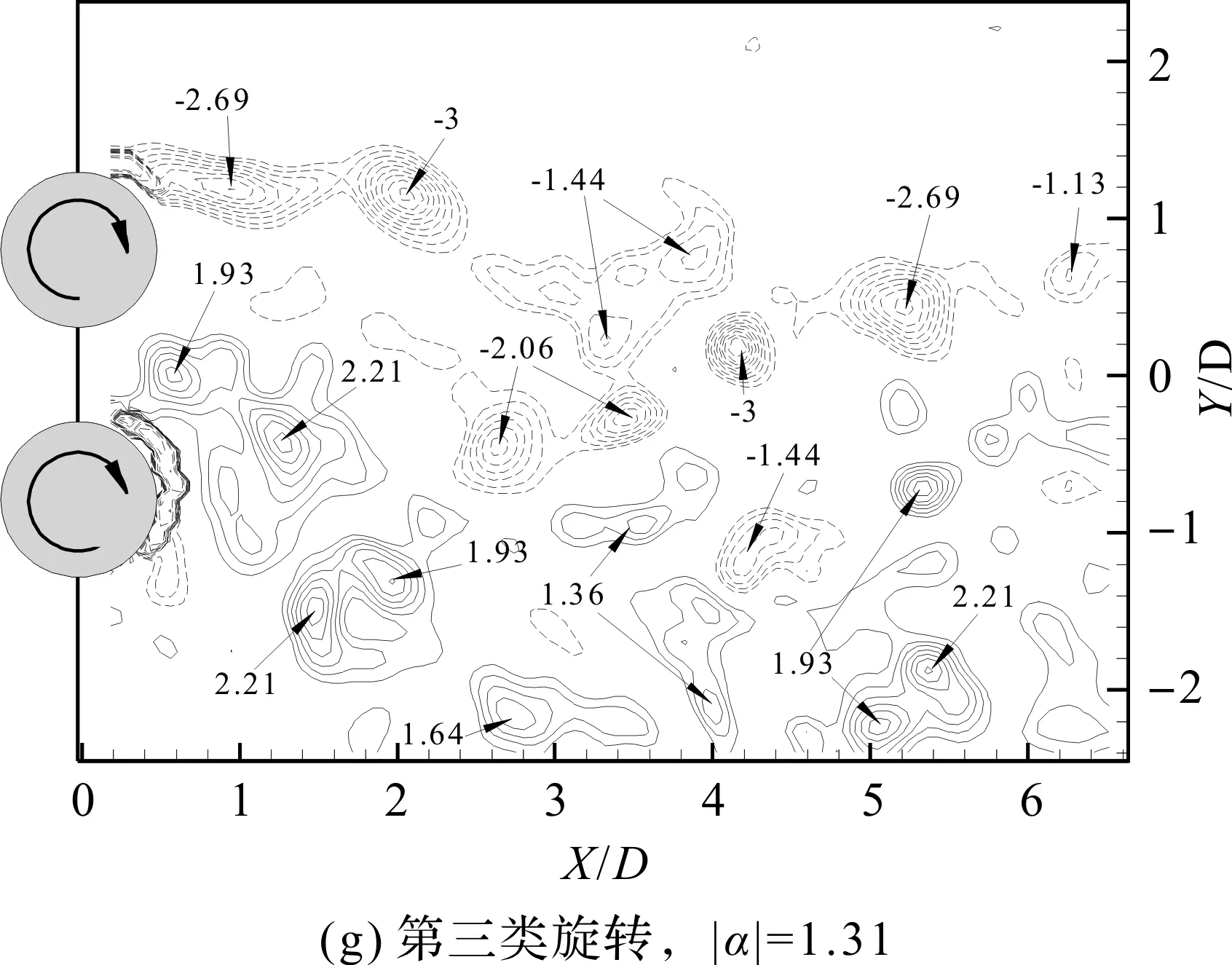
两圆柱按第二类旋转方向转动，|α|增至1.31(图4(e))，漩涡分布的范围和涡量大小与圆柱静止时的情况基本一致，不同的是漩涡脱落的位置提前至X/D=2D，上、下两圆柱的尾迹基本对称；当|α|提高到1.74时，漩涡脱落的位置继续往上游发展，间隙流的速度明显增大。当|α| 提高到2.62时(图4f)，涡量强度增强，漩涡的分布更加分散。相对于低雷诺数[10]，在中等雷诺数下，第二类旋转方向的圆柱尾涡的分布更广，漩涡的数量较多，湍流强度较大。当并列圆柱做第三类旋转时(图4g,h)，|α|越大尾迹整体向下偏转的角度越大，|α|的增大使涡脱落的位置向X轴负方向移动，但并未消减涡量强度，上圆柱外侧和间隙流处的涡量大小仍保持在2 s-1的水平。综上，间距比为1.6时，第一类旋转对尾迹漩涡的消减效果最佳，其它两类旋转方向下，|α| 的增大使漩涡的脱落位置向X负方向偏移，而对尾迹涡量强度的影响不大。

2.2 时均速度场及湍动特性分析

以下结合时均速度场(U∞为来流速度，U为时均速度)及湍流度(Tu=u’/U，u’为湍流脉动速度的均方根)分布图对并列旋转双圆柱绕流场的湍动特性进行分析，重点探讨间距比T/D=1.6时，|α|和旋转方向对圆柱尾迹湍动特性的影响。

当间距比T/D=1.6，由图5(a)可知，静止并列圆柱的尾迹存在明显的速度降，表明此时尾迹中有较强的漩涡结构及运动。当-1D≤Y/D≤1D，在0.6D≤X/D≤8.6D区域内湍流度在20%～40%之间(受间隙流影响，Y/D=0附近个别点除外)、在X/D≥10.2D区域内的湍流度则降至20%左右，此时近尾迹的湍流运动较为激烈。

如图5(b)、图6(b)所示，当圆柱做第一类旋转，转速较小时双峰速度降分布只存在于近尾迹的前两个剖面上，湍流度的双峰分布则消失；速度降整体有明显下降，大于10%的湍流度分布范围迅速缩小；X/D≥5.4D的远尾迹区域，速度降减小至20%以下，-1D≤Y/D≤1D区域内的湍流度则低于10%。随|α|增大到1.74，双峰速度分布也随之消失，各剖面上的速度降都有较大幅度地减小，较大湍流度分布的范围继续缩小，如图5(c)、图6(c)所示。对于|α|=1.74的较低绕流速度，在远尾流X/D≥5.4的第一类旋转绕流下的湍流强度降低到相当于自由来流的水平，并且在更靠近的尾流X/D≤1.4处，也可以减弱。这表明圆柱做第一类旋转时，相对速度的提高压缩了漩涡向下游演化发展的空间，同时削弱了尾迹的湍流运动。当圆柱做第二类旋转时(图5(d)、图7(a))，随|α|的增大，-1D≤Y/D≤1D区域内的速度降和湍流度减小到一定程度后保持相对恒定，间隙流从圆柱壁面获得更高的初始速度，因此间隙流对下游的影响范围也更大；当|α|增至1.74(图5(e)、图7(b))，X/D≤5.4D的剖面时均速度都呈双峰分布；X/D≥10.2D，-1.5D≤Y/D≤1.5D的远尾迹仍分布有20%的速度降、12%的湍流度。可见，圆柱做第二类旋转时，|α|的提高能一定程度消减尾迹的漩涡结构和湍流强度，但效果不如第一类旋转，而间隙流对尾迹的作用与圆柱静止时相比明显增强。当圆柱做第三类旋转时(图5(g)、图7(c))，随|α|的增大，主要的速度降分布区域皆向下偏移，0.6D≤X/D≤4.6D内较大速度降的分布范围有所缩小、降幅基本不变；|α|的增大对远尾迹速度降大小的影响很小。通过比较图7(c,d)可知，|α|的增加只能使主要湍流度(≥20%)的分布区域发生偏移，但并不能消减尾迹的湍流强度，当|α|增至1.74时(图5(h)、图7(d))，湍流强度仍与圆柱静止时接近，其主要分布区域则平均向下偏移1D左右。对于第二类和第三类旋转，即使绕流速度从|α|=1.74增加到|α|=2.62，接近我们的实验装置的上限，但相当大的分布范围内的湍流强度仍然接近8%。

图5 间距比为1.6时的时均速度场Figure 5 Time-average velocity field of T/D=1.6

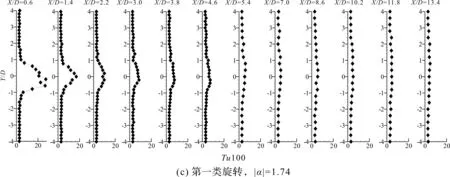
图6 间距比为1.6的湍流度分布图Figure 6 Distribution of turbulence for T/D=1.6

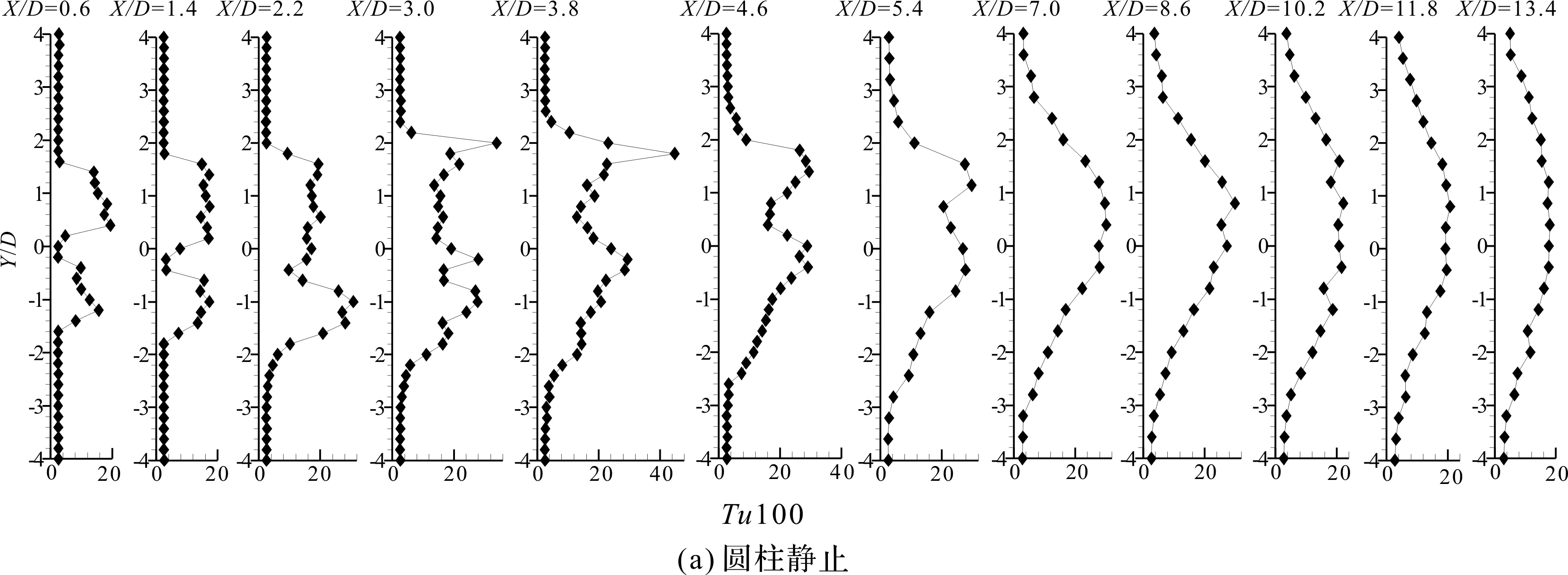
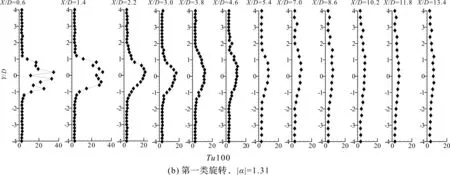
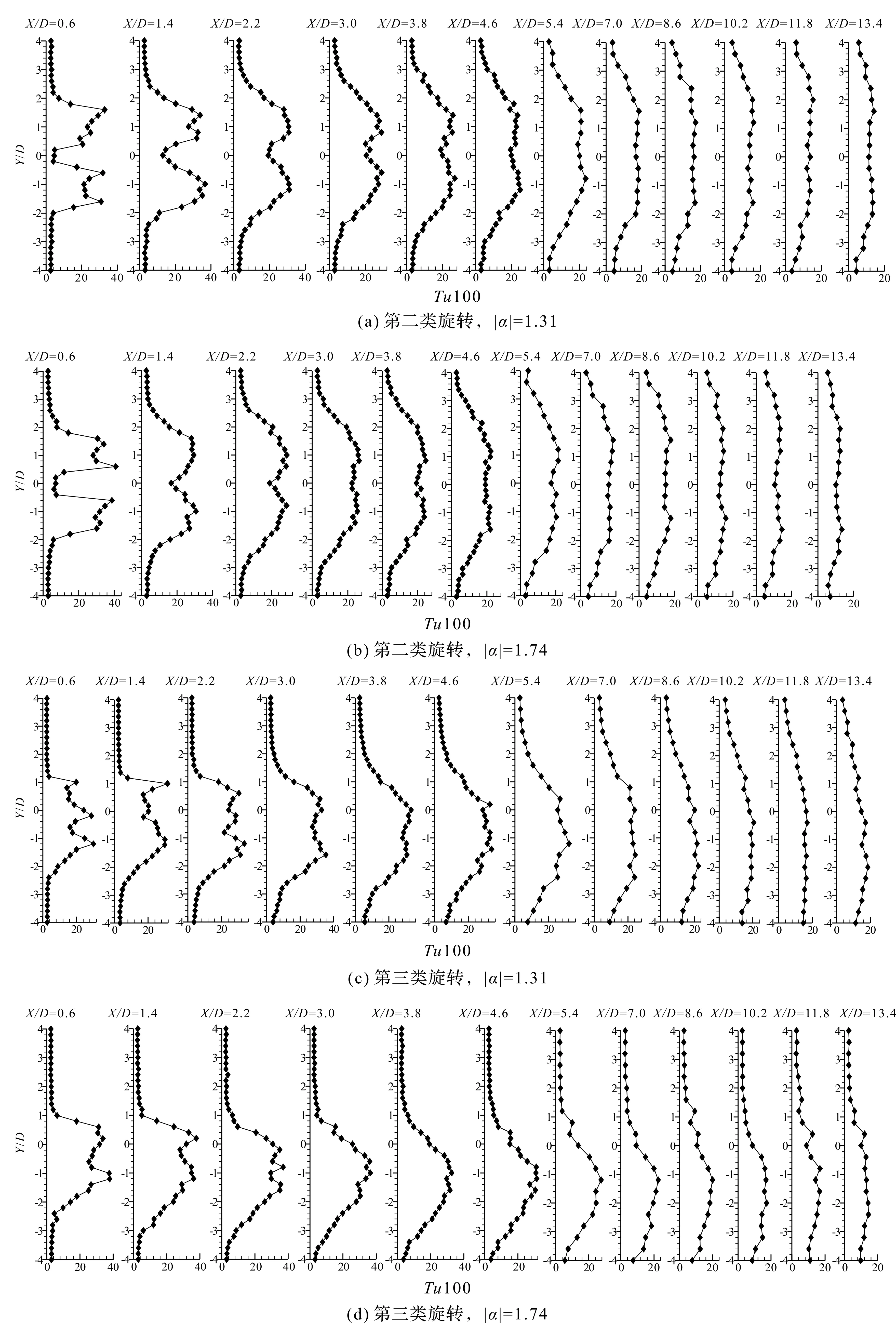
图7 间距比为1.6，第二类旋转和第三类旋转的湍流度分布图Figure 7 Distribution of turbulence for T/D=1.6(The second and third rotation types)

3 结 论

本文利用PIV技术和热线风速仪对Re=950下的并列旋转双圆柱绕流进行了实验研究。实验结果的分析基于瞬态涡量场、时均速度场以及湍流度分布。其中瞬态涡量场利用PIV系统采集的瞬态速度矢量场经数据后处理得到，时均速度场和湍流度分布由热线风速仪所采高频速度信号整理而得。

通过对瞬态涡量场、时均速度场及湍流度分布的分析可知，间距比为1.6D，第一类旋转是对尾迹漩涡消减效果最好的旋转方向，此时相对速度的提高能迅速压缩漩涡向下游演化发展的空间，缩小漩涡结构分布的范围，进而有效消减尾迹中的涡量和湍流强度，使时均速度场更趋均匀。当|α|≈2.18时，对尾迹漩涡消减效果最优。第二类旋转方向反而扩大了漩涡的分布范围，同时间隙流对尾迹的作用与圆柱静止时相比明显增强，使速度和湍流度都出现双峰分布。对第三类旋转而言，|α|的增大只能使尾迹中主要的时均速度降、大湍流度(≥20%)以及漩涡的分布区域一起向下偏移，但是并不能消减尾迹的漩涡和湍流强度，对速度降大小的影响也很小。三种旋转方向下|α|的增大，一方面将引起漩涡脱落位置向上游提前，另一方面将引起尾迹流型发生改变。