高均匀度直下式LED平板灯设计

吴一新，孔剑虹，聂李迅，厉 强

(横店集团得邦照明股份有限公司，浙江 东阳 322118)

直下式LED平板灯的LED光源多采用折射式旋转对称光学曲面的设计，尤其是多曲面的设计，一方面避免单折射面对光线偏折能力的限制，另一方面可以在照明设计中增加额外的自由度。潘诗发等[1]设计了一种近场均匀照明的自由曲面大角度透镜，其内曲面为椭圆形曲面、外曲面为自由曲面；并分析了椭圆形内曲面的长短轴比值对透镜菲涅耳损耗和照度均匀性的影响。陈浩伟等[2]设计了一种带有圆锥台光学元件的超薄直下式LED平板灯，利用漫反射背板和反光圆锥台结构增加了混光距离，提高平板灯均匀度。庞培元[3]设计了两种兼具反射、投射作用的混光元件结构：棱台结构和半球型结构，将其应用于超薄直下式LED平板灯，大幅度提高出光均匀度。这些方法实现了较好的照明均匀度，但是灯具厚度仍然较大。单孝忍[4]设计一种带半圆柱微透镜的超薄平板灯，上半部分是竖放的圆柱、下半部分是横放的半圆柱阵列，实现照度均匀度95.53%、光效率95.99%、厚度仅为15 mm，设计中使用了多个配光原件，则提高了装配的难度和成本。

本文针对上述工作存在的不足，设计薄型化直下式LED平板灯，通过推导自由曲面的偏微分方程，求解自由曲面的离散数据点，利用几何法构建多自由曲面，实现在短距离满足大面积均匀照明的直下式LED平板灯。

1 设计原理

1.1 单自由曲面微分方程

如图1所示，考虑xz平面，目标照明区域的高度为H，半径为R，目标平面上点的坐标为(x,0,H)，θ、γ分别为入射光线、出射光线与z轴的夹角，α为入射角，β为出射角，轮廓线中心高度为r0，r为轮廓线在θ方向上的极半径，系统材料折射率为n。

图1 自由曲面光学系统轮廓线Figure 1 Contour of free surface optical system

根据微分几何关系可以用极坐标系下的微分方程表示光学系统的轮廓线：

dr=-r·dθ·tan(α)。

(1)

假设LED点光源发光呈朗伯型分布，其光强分布I(θ)满足

I(θ)=I0·cos(θ)。

(2)

式(2)中：I0为LED沿轴线方向的光强。根据光源发出的光和入射到目标平面上的光之间的能量守恒，可以得到

(3)

式(3)中：E(x)为目标平面上的照度分布，对于均匀照度而言，E(x)=E0。由式(2)和式(3)，可以得到目标位置x和光源入射角度θ之间的映射关系：

x=R·sin(θ)。

(4)

LED平板灯单颗透镜的要求是在照明区域内照度均匀，

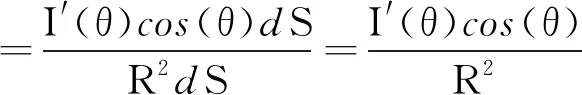
(5)

0～θ角之内LED光通量占总光通量的比例为

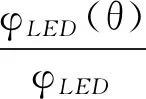
(6)

单颗LED的总光通量为

(7)

透镜的作用是把LED光源的θ角光转变为LED单颗透镜下的σ角出射光，见式(8)：

(8)

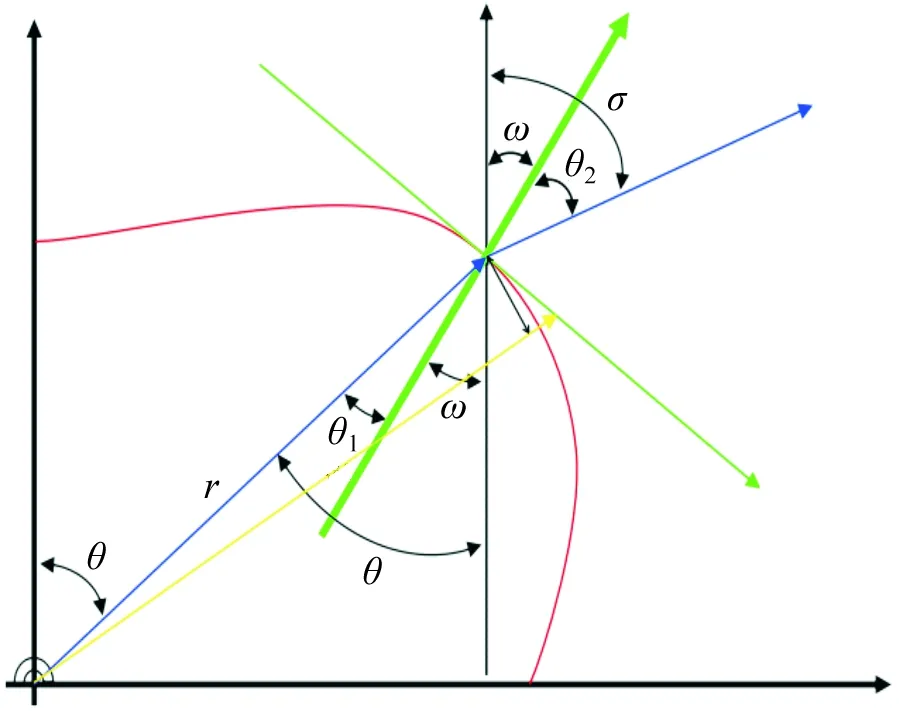
图2 自由曲面光线图Figure 2 Free surface light

1.2 自由曲面的几何构建法求解

由于解析法求解的复杂性，采取几何构建方法可以直观、简洁的构建自由曲面的轮廓线。如图3所示，根据式(3)和式(4)建立入射角度θ和目标落点位置x之间的映射关系，对θ和x进行相应划分。然后，在轮廓线上指定一个初始点P0，根据指定的映射关系和Snell定律就可以求得P0点的法线矢量N0：

图3 基于几何法数值构建透镜轮廓线Figure 3 Construction of lens contour based on geometry

N0=(noO0-niI0)/|noO0-niI0|。

(9)

式(9)中：I0和O0分别是P0点处的入射光线和折射光线的单位矢量，nI和nO分别是透镜和透镜周围材料的折射率。通过求解下一条入射光线I1与P0点的切平面的交点就可以得到轮廓线上的下一点P1，且根据指定的映射关系和式(9)就可以求得P1点的法线矢量N1。重复上述步骤，就可以求解出透镜轮廓线上的离散特征点：P1、P2、…、PN。

单自由曲面在光线大角度出射时，容易发生全反射，使得照度均匀性变差、出光效率降低。采用双自由曲面可以提高系统的折射能力，减少全反射现象，提高目标面照度均匀度和出光效率。

设内曲面对应的目标照明区域的半径是R1，外曲面对应的目标照明区域的半径是R2，并假设内、外曲面都可以实现均匀的照度分布，内外曲面目标位置和光源角度之间的映射关系如下：

(10)

式(10)中：N是入射角度θ划分的数目，x1i和x2i分别是内外曲面对应的目标落点位置。

根据映射关系就可以通过几何构建方法分别获得内外两个曲面的离散数据点，如图4。首先，分别给定内外轮廓线中心的两个初始点P10和P20以及其法线矢量N10和N20，从而可以求得P10和P20点的切线。光源发出的下一条角度为θ1的入射光线I1与P10处的切线的交点P11作为内轮廓线上的下一点。根据映射关系可知，入射光线I1经过P11点之后的出射光线在目标上的坐标位置为x11，即P11点处的出射光线方向矢量O11已知。O11与P20点处的切线的交点P21作为外轮廓上的下一点。同理，根据映射关系可以得到P21点处的出射光线方向矢量O21已知。由snell定律可以获得点P11和点P21处的法线矢量N11和N21。紧接着，再考虑光源发出的下一条角度为θ2的入射光线I2，重复上述步骤便可以获得内外两条自由曲面轮廓线的离散数据点，从而可以获得双自由曲面的3D模型。

图4 双自由曲面的几何构建方法Figure 4 Geometry construction method of double free surface

2 基于双自由曲面透镜阵列的平板灯设计与仿真

平板灯的单个透镜单元的结构参数如图5所示，目标照明平面距离光源H=20 mm，产生的均匀照度光斑的半径R=80 mm。透镜的内表面高度d1=5.5 mm，外表面高度d2=6.5 mm。透镜的材料为PMMA，折射率为1.493。LED光源的尺寸为1 mm×1 mm。点光源的光线追迹图如图6所示，点光源发出的光线经过双自由曲面的折射，在距离光源20 mm的平面内可以精确的产生半径80 mm的光斑。

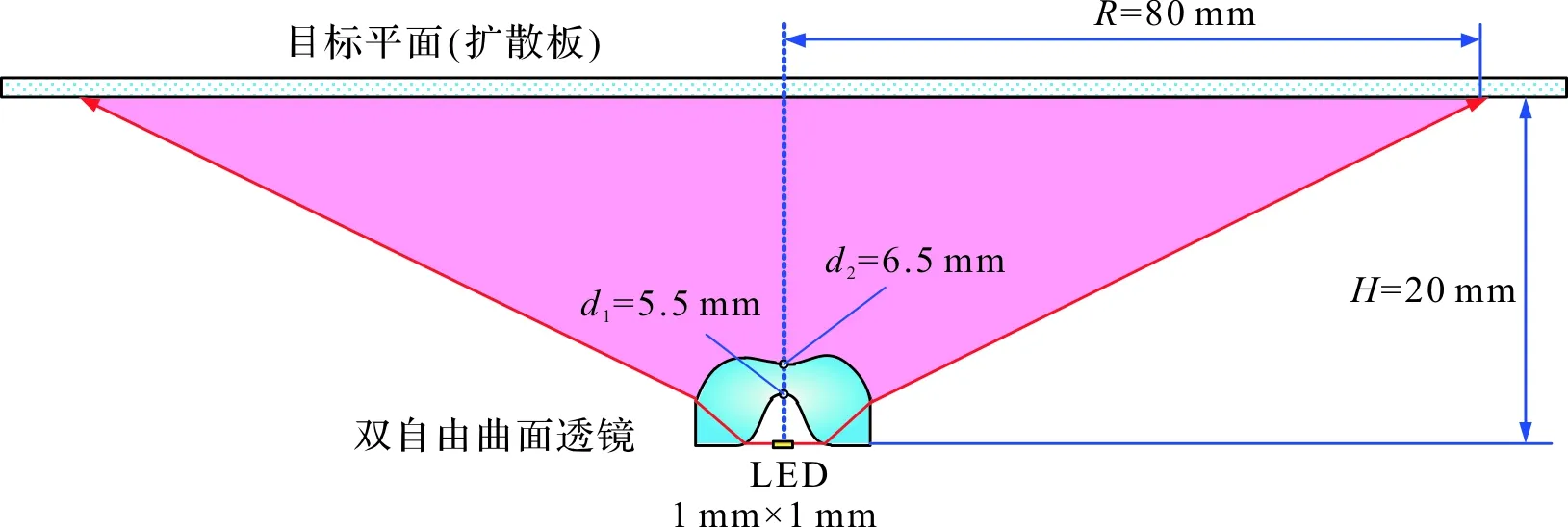
图5 双自由曲面透镜设计参数设置Figure 5 Design parameters of double free surface lens

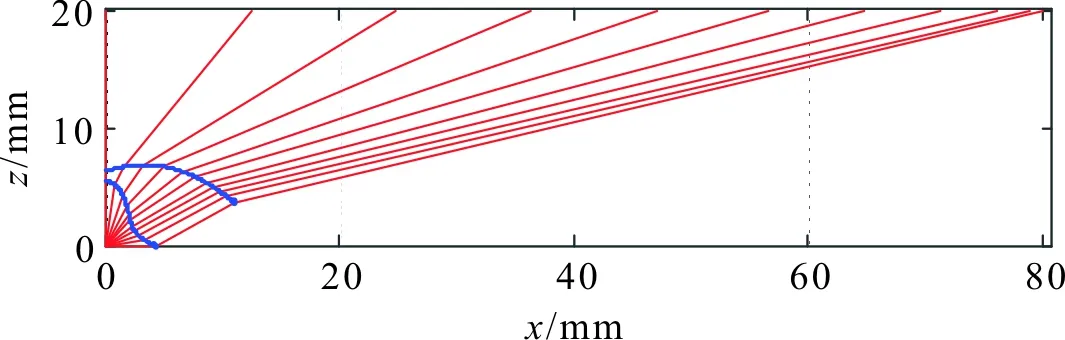
图6 点光源的光线追迹图Figure 6 Light trace of point light source

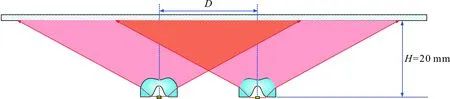
图7 基于双曲面透镜阵列的LED面板灯结构参数Figure 7 Structure parameters of LED panel lamp based on hyperbolic lens array

平板灯表面的照度分布是由各双自由曲面透镜单元的照度分布叠加在一起产生的。优化系统找出最优透镜间距D。

假设单个透镜单元在目标照明面上的照度分布为E0(x,y)，透镜单元之间的间距为D，则叠加之后的目标平面上的照度分布E(x,y)为

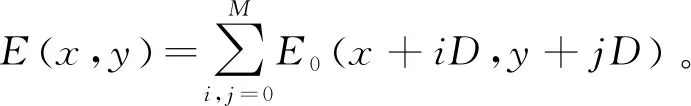
改变透镜间距D值，可以获得不同照度均匀度的设计方案，通过Matlab优化算法，在平板灯表面区域获得满足照度均匀度(最小照度/最大照度)大于0.9的最大的D值。当D=60 mm(即D/H=3时)可以获得大于0.93的照度均匀度，如图8所示。图9为采用Tracepro软件仿真分析得到的照度分布。

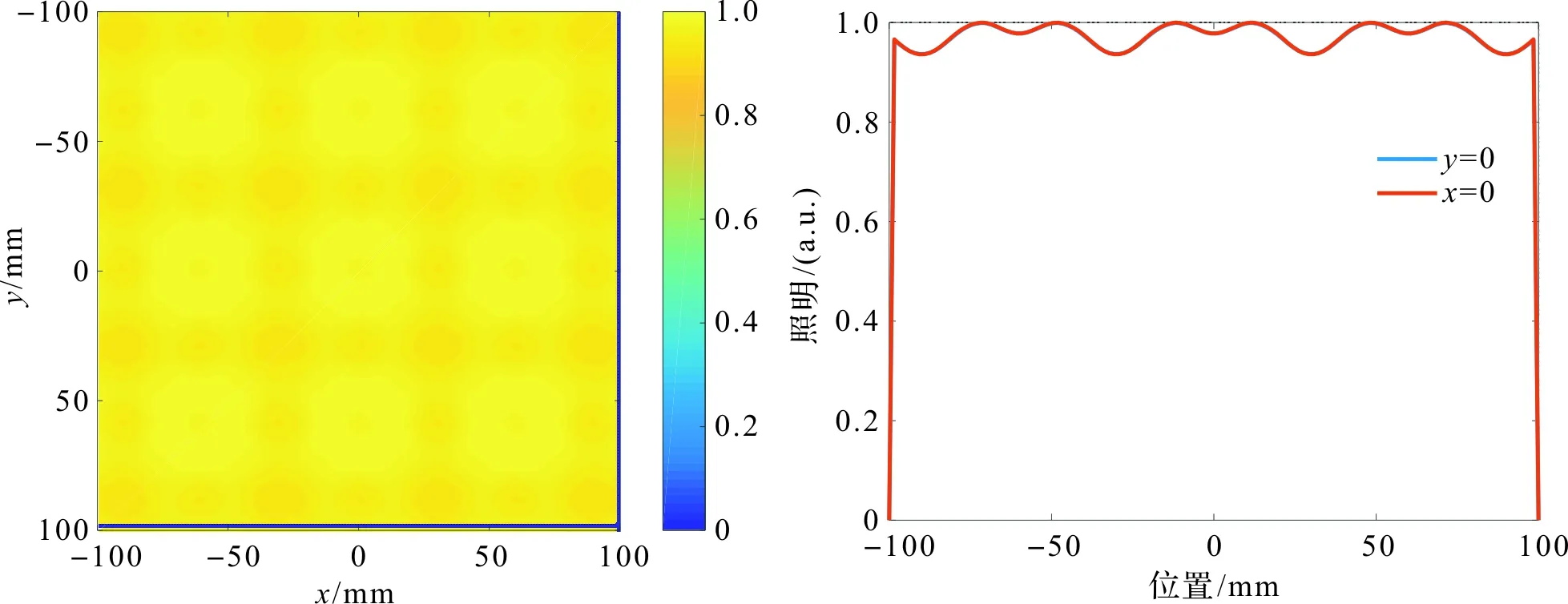
图8 Matlab计算D=60 mm、H=20 mm时平板灯表面的照度分布Figure 8 Illumination distribution on the surface of flat with matlab (D=60 mm、H=20 mm)

图9 Tracepro仿真D=60 mm、H=20 mm时平板灯表面的照度分布Figure 9 Illumination distribution on the surface of flat with Tracepro (D=60 mm、H=20 mm)

3 结 语

采用几何构建方法构建了一款大角度均匀照明的双自由曲面透镜，用1 mm×1 mm LED光源进行仿真时获得了较好的照度均匀性。同时，将双自由曲面透镜进行阵列照明，实现了距高比3∶1的平板灯的设计，距高比是传统基于常规封装LED芯片阵列的直下式平板灯的3倍，可以将LED芯片的数量降低9倍，从而有效地提高LED平板灯的性价比，且减小了平板灯的厚度。