高温下拉制毛细管热力耦合场数值模拟
2021-08-12张火明陈国庆陆萍蓝余润梁管卫兵
张火明,陈国庆,陆萍蓝,余润梁,管卫兵
(1.中国计量大学 计量测试工程学院,浙江 杭州 310018;2.中国计量大学 工程训练中心,浙江 杭州310018;3.自然资源部第二海洋研究所,浙江 杭州 310012)

图1 无接触拉管工艺Figure 1 Contactless tube drawing process
近年来,国内外的很多学者对玻璃管的研究主要集中在加工制造方法、理论分析和材料特性参数等方面。李海蓉等[3]对现有的聚合物挤出过程熔体温度在线计量技术进行了综述,为聚合物挤出工业熔体温度在线计量技术的开发和应用提供了参考。苗培培、饶尧、张伟等[4-6]利用光束传播法对耦合器的拉制过程进行了数值模拟,得到耦合器输出光功率随拉伸长度的变化规律以及光纤拉锥后的内应力变化。陈珊等[7]在2014年设计并制造了一种基于激光加热的玻璃基毛细管拉伸装置,对玻璃管进行拉伸试验,探究实际实验中玻璃管拉伸规律。王珀琥和吴必成[8-9]等通过仿真和实验分析得到了不同温度、拉伸速度、拉力大小、加热时间等因素对玻璃管拉制成形的影响。黄建斌等[10]通过有限元方法模拟与仿真,探讨了光纤熔融拉锥后其内应力大小与光纤被加热区域的降温时间的关系。Quentin等[11]通过数值模拟研究了单根光纤成型的基本物理过程和灵敏度,分析研究了关键参数和物理机制对内应力的影响。Xue等[12]首先建立了共轭多相模型,该模型中包含了光纤加热炉的传热,和使用净辐射法评估外部辐射热通量,将蒙特卡罗示踪法与Polyflow仿真软件相结合,以获得各种炉壁和变形预制件之间的所有影响因素。Florians等[13]设计了一种用于预测冷管拉制过程中管径大小的模型,利用此模型还能研究相对厚度对管变形的影响,并通过实验验证该模型的准确性。本文以毛细管为例,考虑石英材料的粘弹性行为,基于顺序耦合热应力分析法,对管坯在高温无接触拉制情况下的成形过程进行数值模拟分析,研究温度和拉伸力等工艺参数对毛细管管成品的几何参数的影响规律。
1 有限元模型建立
1.1 几何模型的建立及管坯拉制控制方程
本文进行模拟的毛细管管坯为内外径尺寸分别为4 mm和6 mm,高度120 mm的薄管模型,加热炉的内外径分别为40 mm、95 mm,高度为100 mm,模型如图2(a)所示。使用ABAQUS软件自带的建模版块建立数值模拟模型,网格均采用楔形单元形状,划分技术为扫掠网格划分,单元类型为C3D6T,共计11 466个节点、15 249个网格,网格如图2(b)所示。加热炉和管坯之间还存在空气,在软件中将加热炉与管坯之间的模型赋予空气的特性参数,材料特性参数见下表1和表2。

图2 毛细管模型及网格划分示意图Figure 2 The Capillary model and the grid diagram

表1 数值模拟模型环境参数
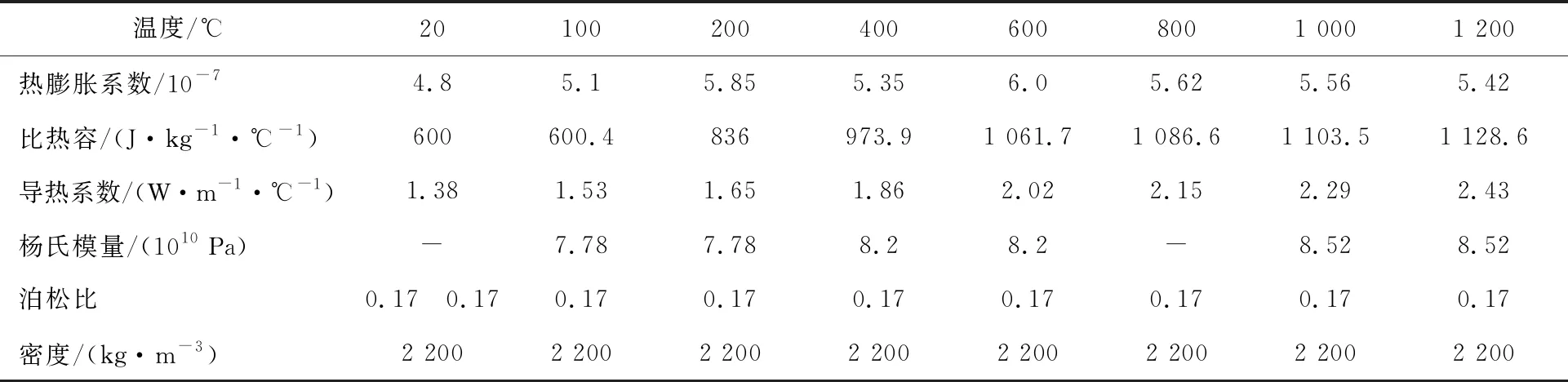
表2 管坯材料特性参数
可将拉制过程看作是非稳态或稳态的不可压缩流动,用Navier-Stokes(N-S)方程来描述,即
(1)
其中,ρ为流体物质密度,v为流体速度,t为时间,p为流体各向压力,F为质量力,μ为流体的动态粘度系数。
在圆柱坐标系下,设管坯熔体的流动速度为v=uez+wer,其中,u,w分别为沿z轴(轴向)和沿r轴(径向)方向的速度分量,ez为两个方向的单位矢量,在管坯连续稳定拉制的过程中,我们可以将重力的影响忽略,即ρF=0,将N-S方程在z、r方向展开。
z方向上的动量守恒方程为
计算机实验教学中心是地方高校学生计算机实验教学重要基地,在普及计算机知识、全面培养学生计算机应用能力和创新能力中发挥越来越重要作用。地方高校在转型背景下,要不断深化教育教学改革,积极探索计算机实验教学中心的建设与发展,利用有限的资金投入,优化组合计算机资源,实现计算机资源高效、共享利用,建设具有“规模化,功能化、网络化、高效化、安全化、规范化、节约化”的计算机实验教学中心,为未来申请“省级示范中心”打好坚实基础。
(2)
r方向上的动量守恒方程为
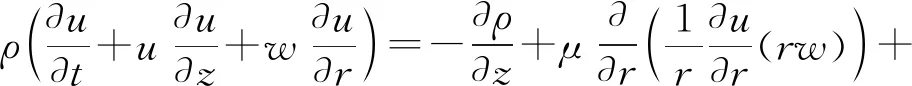
(3)
管坯拉制过程中遵守质量守恒,出入加热炉中的管坯质量保持不变,用方程表示如下:
(4)
对于不可压缩物质,其密度不会随着温度、时间等参量的变化而改变,所以式(4)可改写成[11]
(5)
上述方程构成了熔融管坯流动的二维控制方程组。
根据实际生产情况,将管坯温度设置为25 ℃,空气上方温度为128 ℃,下方温度为35 ℃,加热炉外表面温度为25 ℃,同时通过设置空气与加热炉之间接触面的温度来调整加热炉的加热温度,两个面之间引入间隙热传导来模拟面间的热交换,其他面之间接触均采用罚函数算法;在软件的相互作用属性模块将管坯的六个自由度与管坯下表面的圆心约束在一起,便于拉伸力的施加;温度场选用Coupled Temperature-displacement分析步计算,共计两个分析步。第一个分析步为将坯料送至加热炉中,第二个分析步用来稳定管坯与加热炉内的温度场。分析步设定界面中选择瞬态求解,每个分析步为600 s,步长为固定步长类型,增量步长为10。而在应力应变场的计算则选择Visco分析步,分析步步数和时间的设置均与温度场一致。第一个分析步用于将管坯送入加热炉内,第二个分析步施加拉伸力;输出选择S、U、NT11等场变量,研究温度和拉伸力对成品的外径和壁厚的影响。
1.2 数值模拟方法的选择
在毛细管拉制数值模拟过程中,涉及到温度和变形,需要对应力应变场和温度场两个物理场进行耦合分析。ABAQUS中提供了顺序耦合和完全耦合两种求解耦合热应力的方法。成型过程中,毛细管的应力应变场对温度场的影响较小,故采用顺序耦合热应力分析,先求解加热炉内和毛细管的温度场,再将温度场的计算结果文件作为预定义场导入到应力应变场的计算中,计算出此温度场下毛细管的应变。
数值模拟所采用的毛细管材料为石英,是一种热流变材料,其粘度随着温度的升高而降低,在数值模拟过程中应对材料的粘弹性行为加以考虑[11]。热流变材料满足时温等效性,即在较高的温度和较短的应力松弛时间情况下获得的应力松弛变量,与较低的温度和较长的应力松弛时间情况下获得的结果可认为是相同的。在ABAQUS软件中的时温等效模型为WLF方程,该方程适用于高分子聚合物的粘弹性分析过程,而Arrehenius公式对玻璃等非晶体材料的时温现象的描述比WLF方程更准确,故采用Arrehenius定律来描述毛细管粘度随着温度的变化规律
(6)
式(6)中,T为温度,η(T)为T时刻毛细管的粘度,Tref为参考温度,取293 K,ηref为毛细管在Tref时的参考粘度,取9.565×108N·s/m2,α为与玻璃性质本身有关的参数,取20 270[11]。
根据王炯[14]改进的Maxwell松弛模量表达式,有
(7)
式(7)中,τ为KWW松弛时间,τ=η/G,β为指数扩展因子,这里根据毛细玻璃管的特性,取β=0.5,G为剪切模量或体积模量。
综合式(6)和式(7),利用Fortran语言编写相应的用户子程序,完成变温松弛模量的计算,并参考文献[12]使用ABAQUS自带的Prony级数对应力松弛模量实验数据拟合得到粘弹性参数。
2 模拟结果处理及分析
在实际生产过程中,通过调节加热炉温度、管坯内的气体压力和拉伸力来控制成品的几何尺寸,本文根据实际生产情况,将加热温度T设定在1 100~1 400 ℃范围内,每隔100 ℃进行取值;管内气体压力P保持在0 kPa;拉伸力F范围在450~850 mg,每隔100 mg取一个值。基于顺序耦合热应力分析法的特点,先对加热炉内和管坯的温度场进行数值模拟,再对毛细管拉伸过程中的应力应变进行分析。
2.1 温度场模拟分析
数值模拟中将加热炉与空气相交的内圆柱表面定义为加热面,该面的温度为加热温度,热量从加热炉内圆柱表面逐渐向外扩散。下面以加热温度为1 200 ℃情况为例,对加热炉炉内的温度场进行分析。
从图3中可以看出,加热炉内温度由内到外开始上升,大约从30 s开始达到稳定状态,且达到最大值1 200 ℃。模型中将外表面设置为25 ℃,热量由内表面向外扩散,所以外表面温度要低于内表面。
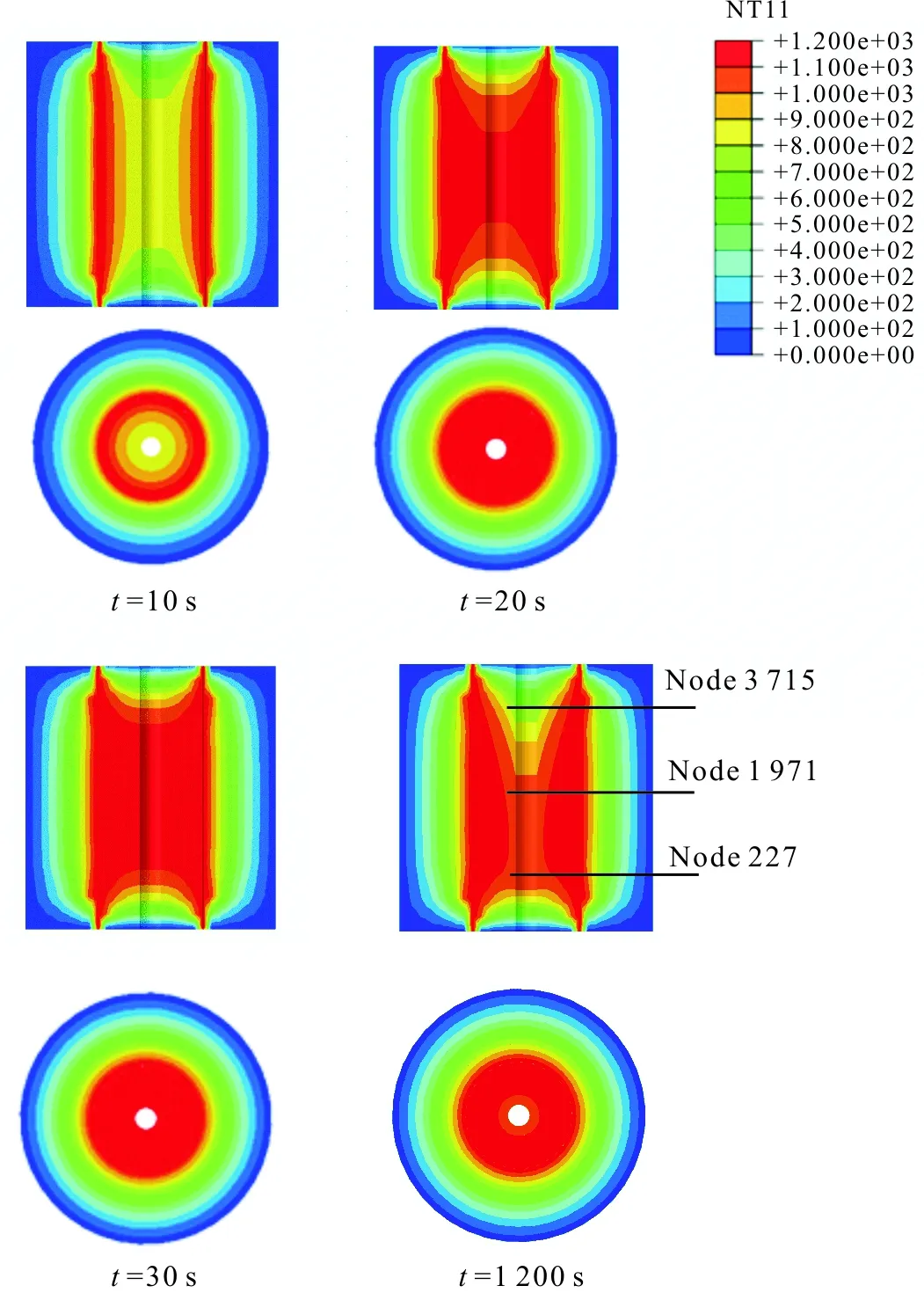
图3 加热炉内温度分布图Figure 3 Furnace temperature distribution map
为了更加直观地对加热炉内不同位置处不同时间点的温度进行分析,选取炉内上中下三点(Node3 715、Node1 971、Node227)进行比较。结合图3和图4,可以看出,三点的温度大约在30 s左右时,都达到了最大值。在大约100 s时,上部节点温度开始急剧下降,这是因为管坯从上往下送进炉内,对炉内温度有一定的影响;随着时间的增加,管坯进入到中部,中部节点的温度开始下降,大约到了600 s左右,第二个分析步生效,管坯不再向前行进,上中两节点的温度开始上升。管坯的运动位置并未达到加热炉下部,故下节点温度受管坯的影响较小,变化较小。
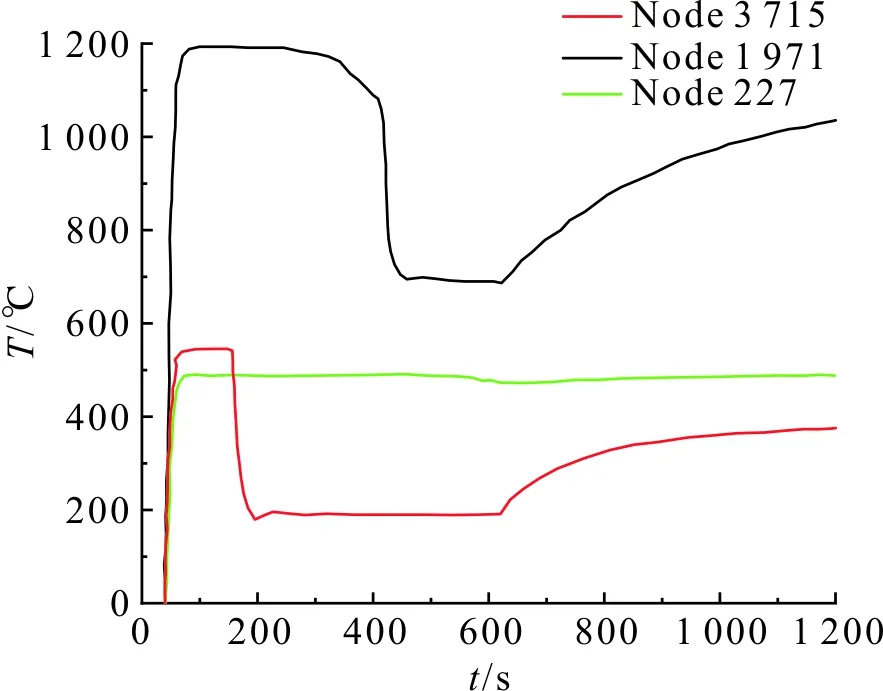
图4 三节点温度变化曲线Figure 4 Three nodes temperature curve
2.2 内外径分析
管坯进入加热炉之后,对其施加不同的拉伸力和加热温度,以分析管坯的外径(R1)、内径(R2)和应力状态变化情况。为了更好地对管坯在t=1 200 s时内外径以及应力状态进行分析,在ABAQUS后处理模块中以成品外表面轴向设置路径Path-1,该路径各点与中心轴线的距离为管坯外径R1;内表面为Path-2,该路径各点与中心轴线的距离为管坯内径R2。图5为管坯熔融拉制之后的流变形状图。

图5 管坯拉制流变形状Figure 5 Diagram of capillary drawing rheological shape
采用控制变量法研究管坯在熔融拉制成型过程中,各影响因素与其径向位移之间的相互关系。保持管坯在熔融拉制过程中的拉伸力在750 mg,管内气体压力设置为0 kPa,改变加热炉的加热温度,Path-1的轴向距离(本文用A表示)与内外径的关系曲线图见图6(a),图6(b)为仿真软件计算云图。结合图6(a)和图6(b)可以看出,当加热温度在1 400 ℃的时候,坯料内外径变化量最大,拉伸长度最长;温度为1 100 ℃时,大约在管坯58 mm左右轴向距离处,加热炉内的温度达到管坯软化温度,管坯在拉伸力作用下,径向位移急剧变大,此时位于加热炉中的管坯形成了外径最小的颈区。由图6(a)可知,随着温度的升高,颈区出现的位置逐渐提前;随着管坯轴向距离的增加,内外径变化量趋于平稳,管坯表面越来越平坦。
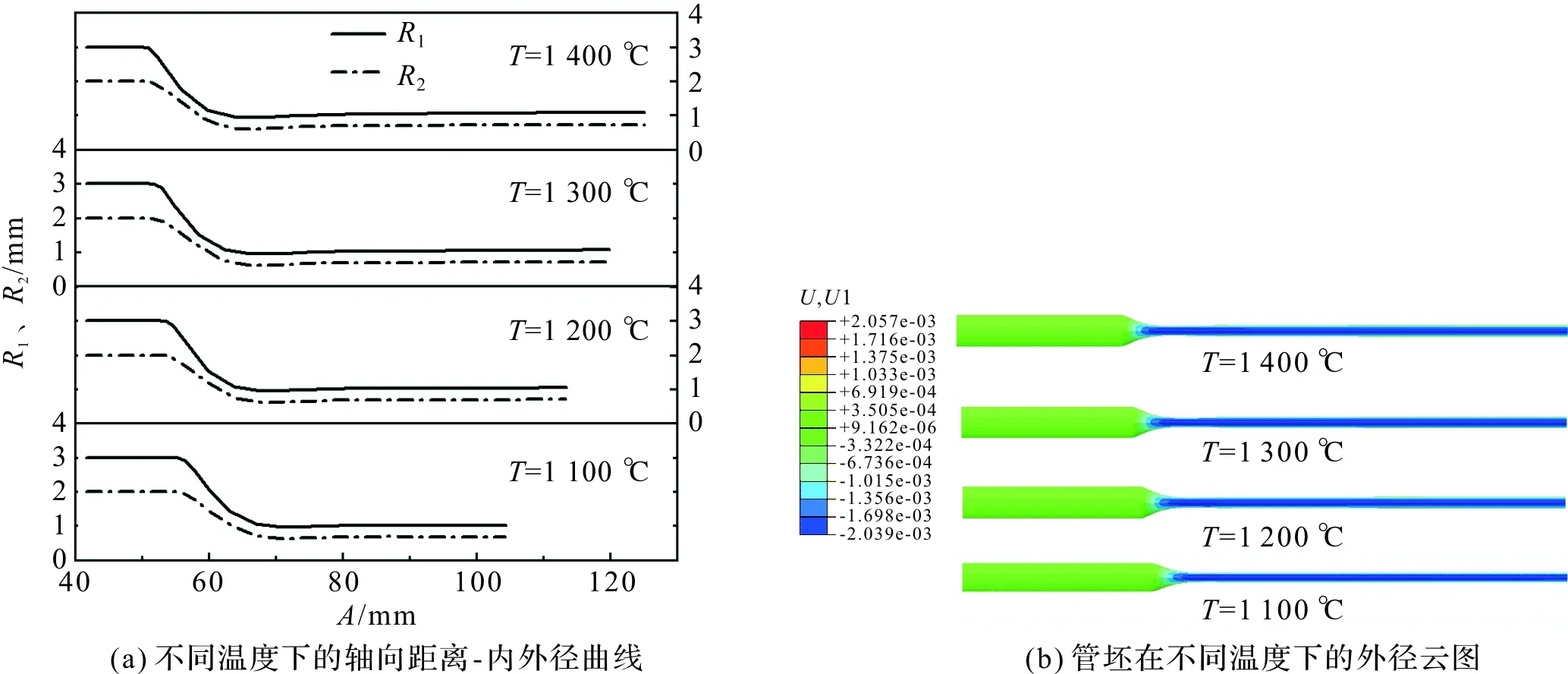
图6 毛细管在不同温度下的轴向距离—内外径曲线,外径云图Figure 6 The axial distance inside and outsidediameter curve of capillary tube at different temperatures, and the outerdiameter nephogram
图7为陈珊[7]通过实验得出的不同温度下的毛细管内外径变化。由图可知,保持其它条件不变的情况下,随着温度的升高,毛细管的直径逐渐变小,这与本实验中得出的结论一致。

图7 不同温度下毛细管内外径变化Figure 7 Variation of capillary inner and outer diameters at different temperatures
将炉内温度控制在1 200 ℃,管坯管内气体压力设为0 kPa,只改变拉伸力的大小。图8(a)为450~850 mg拉伸力下,Path-1的轴向距离与径向位移的关系曲线图。由图知内外径随着拉力的增加呈现逐渐减小的趋势,当拉伸力为850 mg时,颈区中部的壁厚最小。为了更加清晰直观地观察到该现象,本文以管坯在不同拉伸力下的外径为例,截取了管坯在不同拉伸力下的外径云图和与之相对应的颈区局部放大图,如图8(b)。在拉伸力逐渐增大的情况下,管坯的颈缩现象提前出现,颈区处的外径逐渐减小,轴向长度(即拉伸长度)随之增加。
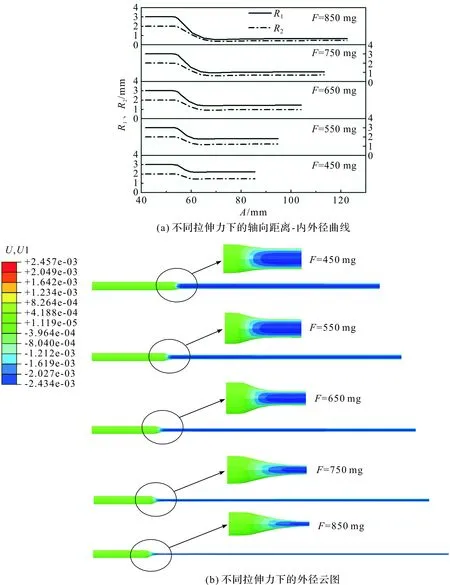
图8 毛细管在不同拉伸力下轴向距离—内外径曲线,外径云图Figure 8 Axial distance inner and outer diameter curve and outer diameter nephogram of capillary tube under different stretching force
保持其它条件不变的情况下,增加拉伸力,拉伸速度也将逐渐增大,所以在研究拉伸力变化情况下对毛细管直径的影响时,可以用拉伸速度与管径变化的对应关系来近似代替拉伸力与管径变化的关系,它们的变化趋势大致相同。图9为陈珊[7]通过实验得出的不同速度下的毛细管内外径变化。
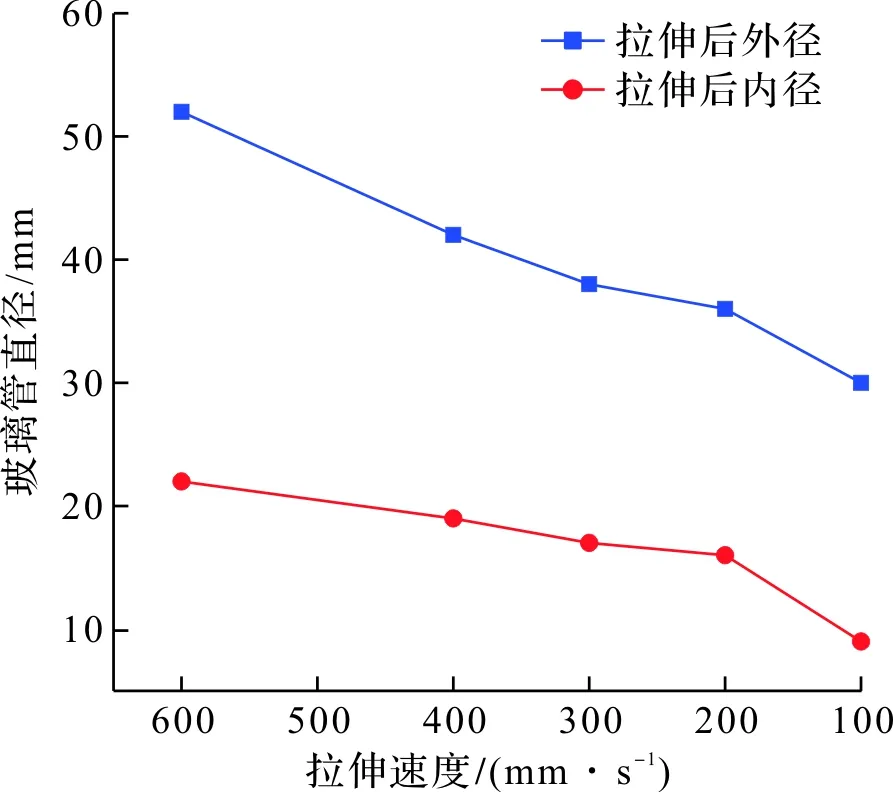
图9 不同速度下毛细管内外径变化Figure 9 Variation of inner and outer diameter of capillary tube under different velocity
2.3 Mises应力分布规律
图10(a)和图10(b)分别是Path-1在不同温度和拉伸力下的Mises应力(本文用M表示)曲线图,从图10中可以看出,Path-1应力峰值第一次出现在轴向距离为0的位置。因为在设置边界条件时,对该位置施加了固定约束,所以在拉伸力的作用下,该位置的应力值稍大于其他位置。第二次峰值出现在轴向距离大约50 mm位置处。图10(a)中,毛细管拉制过程中的Mises应力峰值随着温度的增加而变大;峰值过后,不同温度下轴向各点的应力值波动范围不大,趋于平稳。而在图10(b)中,不同拉伸力下的Mises应力峰值随着拉伸力的增加而变大;峰值过后,不同拉伸力下轴向各点的应力值相差较大,但都趋于平稳,说明管坯轴向受力均匀。
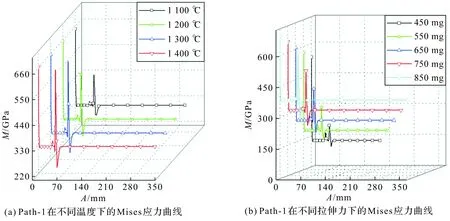
图10 Path-1在不同温度和不同拉伸力下的Mises应力曲线Figure 10 Mises stress curve of path-1 under different temperature and different tensile force
模拟得到的应力分布云图如图11和图12,图11为管坯不同温度下的Mises应力分布云图。

图11 不同温度下的Mises应力分布图Figure 11 Mises stress distribution under different temperatures
从图中可以清晰的看到,Mises应力最大值达到了875 GPa,应力最大值出现位置在管坯左端面,此区域因设定为固定约束,故在拉制过程中Mises应力较大;随着温度的增加,管坯拉伸颈区出现的位置也提前出现,并且在颈区上方大约5 mm左右出现第二次应力峰值,由于该区域的温度未达到管坯软化温度点,而下方区域的温度达到软化点,在拉伸力的作用下,出现第二次应力峰值;拉伸颈区处于变形与未变形区域之间的过渡区域,应力值要远小于其他区域。同样,为了清晰直观地观察颈区应力变化情况,截取了管坯在不同拉伸力下的Mises应力图及局部放大图,见图12。该图中,管坯的管径在拉伸力增大的情况下变得越来越小,而轴向距离越来越大,拉伸颈区提前出现,在颈区位置处的应力比其他区域的要小,与温度升高情况下出现的现象一致。
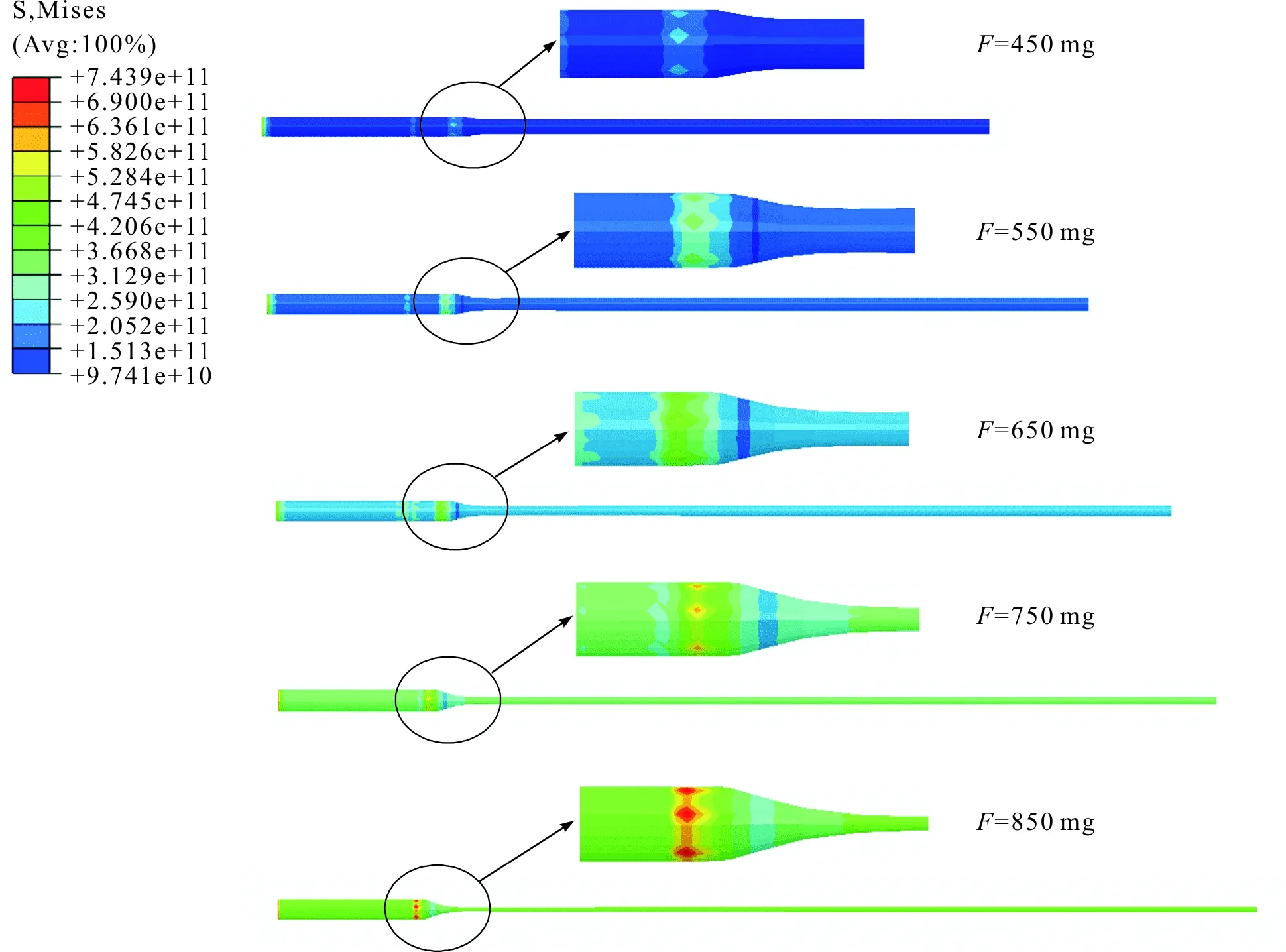
图12 不同拉伸力下的Mises应力分布图Figure 12 Mises stress distribution under different tensile forces
3 结 论
本文首次将顺序耦合热应力分析方法运用到毛细管拉制成型过程中,在管坯拉制过程中设置不同的加热温度和施加不同的拉伸力,通过对管坯的径向位移和Mises应力的变化分析,得到如下结论。
1)在毛细管拉制成型过程中,其内外径与温度和拉伸力成反比:随着加热温度升高,内外径逐渐减小,沿管坯的轴向距离随之增大;随着拉伸力增大,管坯的外径逐渐减小,径向位移同样会增大;反之亦然。
2)Mises应力值与温度和拉伸力成正比,并且出现了两次应力峰值;第一次出现在轴向距离为0 mm的位置,第二次峰值出现在拉伸颈区上方5 mm位置处。
3)加热温度升高和拉伸力增大会将拉伸颈区出现的位置提前,并且该区域与其他区域相比,Mises应力值明显较小。
4)在毛细玻璃管拉伸过程中,可以通过控制温度、拉伸力大小等来控制其内外径和轴向距离。随着温度的升高,其拉伸颈区位置提前,应力峰值出现的位置同样会提前,在拉伸过程中应该根据环境温度来确定其应力峰值的位置,保证其拉伸成型的稳定性。
