考虑光伏无功补偿的多馈入直流受端电网强度分析

李羽晨，王冠中，张 静，周靖皓，叶 琳，辛焕海

（1.浙江大学电气工程学院，浙江省杭州市 310027；2.国网浙江省电力有限公司调度控制中心，浙江省杭州市 310007）

0 引言

中国的负荷中心大多分布于东南沿海，以浙江电网为例，已逐步发展为具有高比例直流外受电和高比例新能源的受端电网。多条电网换相换流器型高压直流（LCC-HVDC）输电线路落点于同一受端交流系统，形成了多馈入直流系统［1-3］。同时，以光伏为代表的新能源装机容量和发电量占比不断提升［4-6］。大容量的直流和光伏接入运行需要交流电网具备充裕的电压支撑强度［7-10］。因此，受端电网强度评估对电网运行和规划具有重要意义。

短路比（short circuit ratio，SCR）是量化单馈入直流系统受端电网强度的重要指标［11］，比较短路比与临界短路比（critical short circuit ratio，CSCR）的相对大小可以判断系统在额定工况下的稳定裕度［12］。短路比指标的优势在于计算简单且物理意义清晰，为此，国内外学者针对多馈入直流系统电网强度评估问题，提出了多种短路比指标。基于国家大电网会议（CIGRE）组织直流工作组提出的定义，文献［13］提出量化直流间相互作用强度的多馈入相互作用影响因子；文献［14］在此基础上提出多馈入短路比指标；文献［15-16］提出多馈入运行短路比和有效短路比等。上述多馈入系统的短路比指标缺乏单馈入系统中短路比的物理意义，无法像单馈入直流系统一样精准度量电网强度。事实上，指标及指标的临界值2个量才能决定系统的稳定裕度，故好的指标需要满足2个条件。一是指标公式简单；二是指标临界值容易科学计算，例如，多馈入系统的临界值就等于单馈入系统的临界值。CIGRE所定义短路比满足前者，但不满足后者。为此，文献［17］提出了广义短路比（generalized short circuit ratio，gSCR），克服了经验类短路比指标物理机理不清晰的问题，且同时满足上述2个条件。同时，广义短路比与临界广义短路比（critical generalized short circuit ratio，CgSCR）之间的相对大小能够准确量化系统的稳定裕度。然而，广义短路比并没有考虑光伏电站接入的影响，从而无法分析光伏电站对受端电网强度的影响。光伏电站与电压源换流器型高压直流（VSC-HVDC）输电同属于电压源型变流器，已有学者在CIGRE定义多馈入短路比的基础上分析了VSC-HVDC对LCC-HVDC电网强度的影响［18-19］。然而，光伏与VSC-HVDC在控制方式上不同，且上述研究普遍采用了经验类短路比指标，少见基于广义短路比指标的光伏电站接入多馈入直流系统的研究。

因此，本文基于特征值灵敏度，从定性分析和定量评估2个方面研究了多种控制方式下光伏电站接入对多馈入直流受端电网静态电压稳定裕度的影响。最后，通过仿真算例验证了所提方法的有效性。

1 含光伏电站的多馈入直流系统模型

电力系统静态电压稳定性的临界条件与潮流雅可比矩阵奇异性直接相关［20］，故本文首先从系统的准稳态模型出发，建立系统雅可比矩阵。

电网模型如图1所示。系统包含多回直流和1个光伏电站，受端交流系统对应戴维南等效电路。图中:Pd1、Pd2、Qd1和Qd2分别为两回直流注入受端交流系统的有功和无功功率；Ppv和Qpv分别为光伏变流器输出的有功和无功功率；I1、I2、I3分别为两回直流 和 光 伏 变 流 器 输 出 的 电 流；Pac1、Pac2、Pac3、Qac1、Qac2、Qac3分别为两回直流和光伏变流器向受端交流系统传输的有功和无功功率；E1∠φ1、E2∠φ2、E3∠φ3分别为3个交流系统的等效电压源；Bc1和Bc2分别为母线1和母线2上并联的无功补偿装置参数；Z11∠θ1、Z22∠θ2、Z33∠θ3分别为3个交流系统的等值阻抗；Z12∠θ12、Z23∠θ23、Z13∠θ13分别为联络线阻抗。

图1 多馈入直流系统模型Fig.1 Model of multi-infeed DC system

1.1 交流电网端口特性

本文讨论直流均运行在额定工况下，即端口电压U1、U2、U3均 为1 p.u.，两 回 直 流 额 定 功 率 比 为PN1∶PN2=1∶k。当直流和光伏电站工作在额定工作点时，从直流/光伏侧看进去的受端交流电网的端口线性化方程可近似为［21］:

式中:ΔP和ΔQ分别为各节点有功、无功功率的变化量；U为各节点电压幅值；ΔU和Δδ分别为各节点电压幅值、相角的变化量；Pi为各个端口注入的有功功率，i为馈入回数；B为交流系统导纳矩阵，其中的自导纳Bii＜0；Jnet为交流网络的雅可比矩阵。

B的表达式为:

1.2 直流端口特性

直流系统都采用定功率-定熄弧角控制［22］，其端口线性化方程为［21］:

式中:Ti=2ciK（ci）+2ωBci/（ρiPNi），其中Bci为端口i母线并联的无功补偿装置参数，ω为系统角频率；ρi=Pi/（PNiUi2），PNi为直流的额定容量；Ui为端口母线电压。中间函数K（ci）的表达式为:

式中:γ为熄弧角；Xi为换相电抗；Ki为逆变侧变压器变比；Idi为直流输出电流。

1.3 光伏变流器端口特性

本文主要关注光伏电站的外特性，忽略光伏电站内部的阻抗，不计光照强度和环境温度变化的影响。因此，将光伏电站中的多个光伏逆变器等效建模为一个聚合后的电压源型变流器［23-24］。

传统光伏逆变器通常使用直流电压恒定的Udc控制，可看成是功率源，其雅可比矩阵所有元素均为0，无法对交流电压起支撑作用，且注入的有功功率一般会降低交流电网的电压稳定性。为提升光伏电站对受端电网的电压支撑能力，可以考虑加入交流电压-无功功率下垂控制的方式进行改进，其控制框图如图2所示。图中，PI为比例-积分环节，SVPWM为空间矢量脉宽调制，Hpll为锁相环函数，θPLL为锁相环角度，其他变量含义见附录A。

图2 光伏并网变流器控制图Fig.2 Control diagram of PV grid-connected converter

本文假设光伏电站一般实际运行时功率因数接近1。因为Idref仍然使用定直流电压控制，有ΔP=0。根据图2可得外环控制量之间的关系为:

式中:K为逆变器吸收的无功功率与端口电压之间的下垂系数，K＞0；Ut为光伏逆变器端口交流电压；Utref为交流电压参考值；Qe为光伏逆变器输出的无功功率；Qeref为无功功率参考值。

将式（5）线性化后可以得到逆变器无功与端口电压的外特性关系式为:

式中:ΔQe为光伏无功功率与参考值的差值；ΔUt为端口交流电压与参考值的差值。

则交流电压-无功功率下垂控制下光伏变流器的雅可比矩阵为:

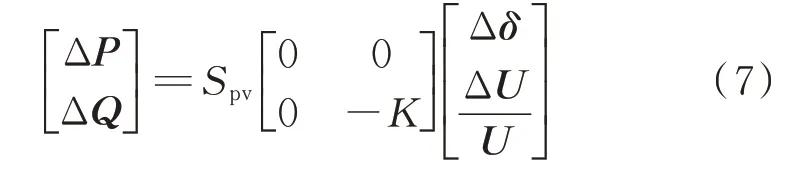
式中:Spv为光伏的装机容量。

通过式（7）可以看出，当光伏电站控制方式为交流电压无功下垂控制时，其外特性雅可比矩阵不为0。稳态时光伏只发出有功功率，当光伏逆变器端口电压发生波动时，逆变器会及时发出或吸收无功功率，以起到稳定受端电网电压的作用。不过光伏仍会输出有功功率影响系统潮流。此时，光伏逆变器对受端电网的影响既有外特性的影响，也有输出有功功率的影响。

2 基于特征根灵敏度的电网强度定性分析

将直流/光伏端口雅可比矩阵与交流网络雅可比矩阵相加后得到系统雅可比矩阵，其奇异性对应系统临界稳定条件。下面先分析交流网络雅可比矩阵主导特征值对矩阵元素的灵敏度，根据交流网络灵敏度分布规律，可以定性分析直流/光伏电站对系统静态稳定特性的影响。

由于静态电压失稳临界条件是直流/光伏端口特性与交流网络端口特性相加所得系统雅可比矩阵奇异，故式（1）中受端交流网络的雅可比矩阵Jnet为非奇异矩阵，有

由于Jnet对称，其特征值λ1对雅可比矩阵元素akj的灵敏度为［25］:

式中:xk和xj为λ1对应单位化特征向量x中与元素位置匹配的分量。

对于多馈入直流系统，导纳矩阵B是对角占优的负定矩阵，在不考虑直流/新能源的端口特性时，矩阵Jnet一般都能保持对角占优的负定矩阵性质。设Jnet的主导特征值λ1（其中λ1＜0）对应的特征向量x=［xT1，xT2］T，那么特征向量满足:

将式（11）化简可得:

在额定运行条件下，B+diag（Pi）为M矩阵［26-27］（对角元素为负，非对角元素为正），从式（12）可得特征向量元素同号（均大于0）。接着把特征向量x乘以xT，得到一个灵敏度矩阵:

Jsen中的元素值即为主导特征值λ1对矩阵中某个位置元素的灵敏度，此处只保留元素对应的正负符号。可以看出，矩阵对角分块元素符号为正，非对角分块的元素为负。

结合式（9）和式（13）可以得出:如果在Jnet的对角块B中加上一个正数，矩阵的主导特征值会增大，但由于其值本身为负，该值反而向原点靠近，故系统静态电压稳定减弱。同理，如果在Jnet的非对角元素块−diag（Pi）中加上一个正数，系统静态电压稳定性变强。

由上文并结合式（3）和式（7）可以说明，LCCHVDC的加入会使受端电网静态电压稳定性减弱。光伏电站的控制模式为传统直流电压控制时，由于外特性矩阵为0，从外特性上不影响系统矩阵的主导特征值。但是，网络雅可比矩阵中的非对角元素上还会加上其容量/输出有功的负数，所以此时光伏电站会使受端电网静态电压稳定性减弱；当光伏电站的控制模式为交流电压-无功功率下垂控制时，其发出的有功功率会使受端电网静态电压稳定性减弱，而外特性则会加强系统稳定性，电网强度的变化需要综合功率与外特性的共同作用。因此，针对具体问题需要定量计算才能得出最终结果。

3 基于广义短路比的电网强度定量计算

前文定性分析了光伏电站接入对受端交流电网强度的影响，下文将通过计算广义短路比及其临界值的变化来定量评估光伏电站接入影响。定性分析已经说明光伏电站对受端电网的影响是由其外特性和发出的功率共同决定的，那么定量计算的目的在于具体说明这2种因素综合下光伏电站接入对受端电网的最终影响，以及量化影响程度的大小。

下文首先给出不含光伏的多馈入直流系统广义短路比指标［17］，然后根据模态摄动理论［28］，推导出光伏电站接入后的计算方法。

3.1 不含光伏的多馈入直流系统广义短路比

假设系统中不含光伏，如附录A图A 1所示。由于式（3）和式（1）中的雅可比矩阵功率方向相反、大小相同，因此，将2个矩阵相加得到系统的雅可比矩阵Jmsys为:

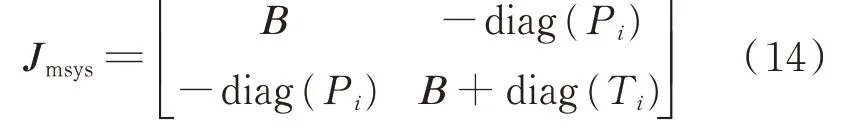
用矩阵的Schur变换将交流系统的无源节点消去，得到系统的降阶雅可比矩阵Jsys0为:

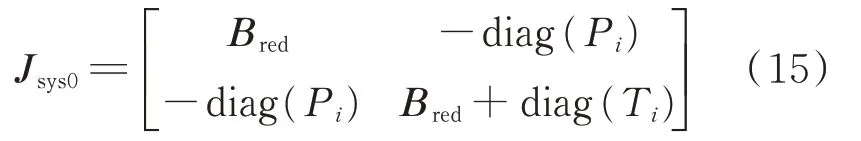
其中，压缩后的导纳矩阵Bred表达式为:

当系统刚好达到静态电压稳定极限时，雅可比矩阵奇异，即

参考文献［17］，上述边界条件等价于式（18）。

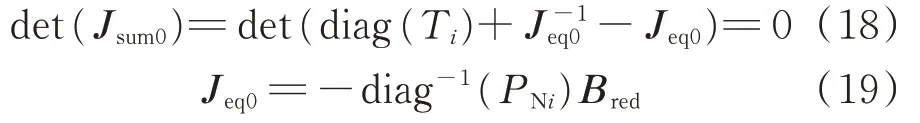
对式（18）中的雅可比矩阵进行模态分解，可以得到行列式的因式分解结果，每个因式分别对应一个等效单馈入系统:

式中:λ0i为Jeq0的特征根，对应每个等效单馈入系统短路比；T为控制参数。

设Jeq0的最小特征根为λ01，对应的左、右特征向量分别为W-1和W，可得:

因为最弱的等效单馈入直流系统决定临界电压稳定，式（20）等价为:

由文献［17］的证明可知，λ01即为多馈入直流系统广义短路比。通过式（22）计算出的λ01为系统在额定运行工况下的临界广义短路比:

从式（24）可以看出，临界广义短路比只与直流系统参数有关，单馈入与多馈入系统的临界广义短路比相等。系统电压稳定等价于广义短路比大于临界广义短路比，且两者差值可以反映系统稳定裕度。

3.2 包含光伏的多馈入系统广义短路比

当系统包含光伏电站时，等效电路如图1所示。根据式（7），设光伏雅可比矩阵为:

式中:Jqv为矩阵右下角元素值。

将加入光伏电站的系统雅可比矩阵同样经过初等行列变换和Schur变换进行压缩，得到系统的降阶雅可比矩阵为:

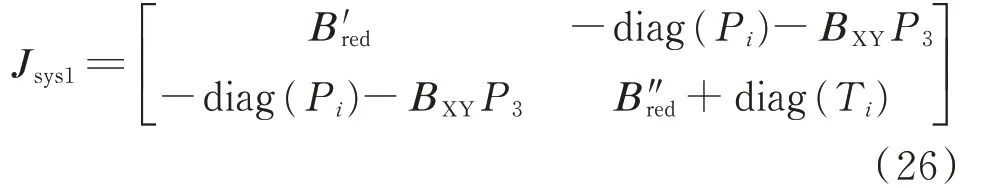
其中，被压缩的节点导纳矩阵因为光伏的接入分成了位于对角和非对角的2块，分别为:

式中:|A|为初等行列变换后右下角矩阵的行列式。

当系统达到临界静态电压稳定时，有

式中:Jeq1=−DB'red；Jeq2=−DB″red；I为单位矩阵。

根据文献［28］中的模态摄动理论，可以将光伏接入后的多馈入直流受端电网看成原本不含光伏的受端网络的摄动。将式（31）看作为光伏未接入的多馈入系统的摄动，进而有:

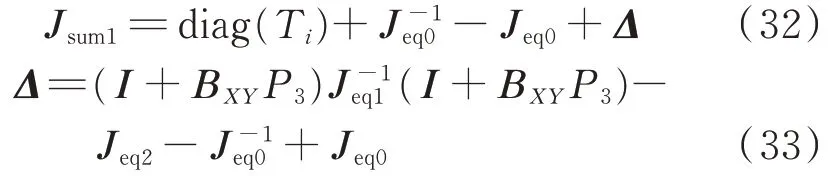
因此，式（32）的临界电压稳定条件经过模态分解后可以近似等价为:

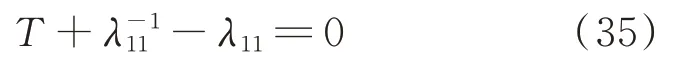
式（35）表明，λ11为光伏电站接入后多馈入直流系统的广义短路比，而临界广义短路比不变，仍为式（35）的解，表达式为式（24）。具体地，含大型光伏电站的多馈入直流系统广义短路比和临界广义短路比的计算和稳定性分析流程详见图3。

图3 短路比计算及静态电压稳定性分析流程图Fig.3 Flow chart of short circuit ratio calculation and static voltage stability analysis

有必要指出，由式（31）可选择将光伏外特性折算到直流侧或交流侧，本文选择后者的理由是光伏电站外特性与LCC-HVDC外特性对网络主导特征值的影响不同，故将光伏归入交流侧进行分析。电网强度的影响结果可通过修正广义短路比或者它的临界值进行计算，例如:文献［29］中对异构多馈入直流系统的强度分析采用的是修正临界广义短路比的技术路线。

3.3 下垂系数选择

根据上文的分析，光伏电站接入受端电网会改变交流网络部分的特征值，而广义短路比可以根据交流网络的主导特征值计算得到。

下垂系数一般可以采用如下原则:光伏电站接入前后，广义短路比保持不变，即式（23）与式（34）的结果相同，以保证光伏的接入不会恶化系统的电压稳定裕度。实际中，可以根据光伏的容量、接入位置进行下垂系数的整定。例如，使用附录A图A 2所示的迭代方法求解。输入各参数和下垂控制系数K的初始值之后，分别算出光伏接入前后交流网络部分的主导特征值，然后求取两者的差值，不断增加K直到差值足够小，此时的K即为最小值。

4 算例分析

为了验证上述定性和定量分析的有效性，以图1所示的三馈入直流系统为模型，在MATLAB中进行算例分析。其中，直流系统使用CIGRE直流工作组提出的标准模型［20］，系统的标幺值基值如表1所示，系统模型的具体结构和元件参数见附录A图A 3。为了更好体现光伏接入对受端电网的影响，构造一弱交流电网，网络参数见附录A表A 1。每个直流系统的控制参数T设置为1.5。光伏的雅可比矩阵采用式（7）推导的结果。

表1 直流系统标幺值基值Table 1 Per unit base values of DC system

4.1 光伏接入对系统雅可比矩阵主导特征值影响

根据第2章中的分析，分别计算未接入光伏电站、传统直流电压控制和交流电压下垂控制的光伏电站接入后的系统雅可比矩阵主导特征值，其中下垂控制系数K为1.5。改变光伏电站的容量，计算出主导特征值与光伏电站容量的关系，两种不同控制方式得到的曲线如图4所示。

从图4可以看出，当光伏电站不提供辅助无功-电压支撑时，系统雅可比矩阵的主导特征值相比于只接入直流更加靠近原点，且随着光伏电站容量的增大逐渐接近原点。说明该控制下光伏电站接入降低了电网的强度；当光伏电站使用交流电压-无功功率下垂控制时，系统雅可比矩阵的主导特征值变得更远离原点，且随着光伏电站容量的增大，主导特征值逐渐远离原点。说明该控制下光伏电站的接入可以增强受端交流电网强度。

图4 不同光伏容量下系统雅可比矩阵的主导特征值Fig.4 Dominant eigenvalues of Jacobian matrix with different PV capacities

4.2 光伏电站接入对广义短路比的影响

根据前文的理论推导，在三馈入直流系统中求解扩展雅可比矩阵Jeq0的最小特征值得到未接入光伏电站的广义短路比，接入光伏之后的广义短路比则通过求解式（34）得到。保持交流网络参数不变，改变光伏电站的容量，分别计算两种外环控制方式（下垂控制采用与4.1节相同的参数）的光伏电站接入前后系统广义短路比的值，如图5所示。

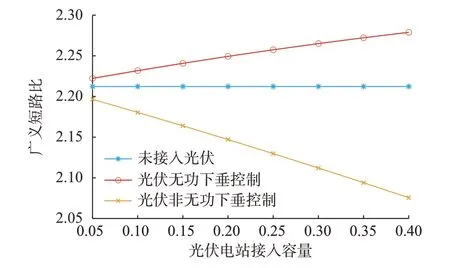
图5 不同光伏容量下系统的广义短路比Fig.5 Generalized short circuit ratios with different PV capacities

从图5可以看出，在给定的直流系统和交流网络参数下，未接入光伏的直流系统广义短路比约为2.21。光伏电站接入后，不同外环控制方式对广义短路比的影响不同。当光伏电站不提供辅助无功-电压支撑时，虽然光伏逆变器的外特性雅可比矩阵为0，但是发出的有功功率仍然对电压稳定造成影响，此时光伏电站相当于一个有功功率源。该控制方式下广义短路比减小，且随着光伏电站容量的增大而呈现单调递减的趋势，说明此时光伏电站的接入会使受端电网的静态电压稳定性减弱，导致电网强度降低。

当光伏电站使用交流电压-无功功率下垂控制时，对受端电网的影响来自其外特性和输出功率的叠加。从图5可以看出，该控制方式下系统广义短路比值增大，且随着光伏电站容量的增大，系统的广义短路比呈现单调递增的趋势。说明此时光伏电站的接入可以有效地提高系统的静态电压稳定性，系统稳定裕度增加，也相当于提高了多馈入直流受端交流电网的电压支撑强度。

4.3 交流电压-无功功率下垂控制系数K的影响

进一步，可研究当光伏为交流电压-无功功率下垂控制时，不同下垂控制系数K对广义短路比的影响。在前文基础上，使K从1变化到2.5，步长为0.5，改变接入光伏电站的容量，仿真结果见附录A图A 4。从图A 4可以看出，其他条件保持不变时，K越大，系统广义短路比越大，光伏逆变器对受端交流电网的支撑作用也越强。当K较小时，例如图A 4中K=1对应的曲线，光伏电站的无功外特性对受端电网的电压支撑作用较弱。由于光伏发出的有功功率会对受端电网静态电压稳定性起负作用，因此，随着接入光伏电站的容量增大，综合效果可能会使电网稳定裕度下降。

此外，改变光伏电站容量，根据前文算法分别计算对应所需要的最小下垂控制系数K，仿真结果见附录A图A 5。从图A 5可以看出，单位功率因数下，随着光伏容量增加，需要设置更大的K，才能保证光伏电站接入不会降低多馈入直流系统的受端电网强度。

4.4 不同光伏容量占比对系统强度的影响

本节仍基于三馈入直流系统，保持直流容量不变，分析交流电压-无功功率下垂控制下不同光伏电站容量所占比例对受端系统稳定裕度的影响。下垂控制参数与4.1节保持一致，光伏容量占直流容量的比例根据远景规划设置为在0～25%变化，分别计算此时的广义短路比和临界广义短路比，求出稳定裕度，仿真结果如附录A图A 6所示。从图A 6可以看出，光伏所占容量比例的变化会改变受端电网的静态电压稳定裕度。光伏电站为交流电压-无功功率下垂控制时，随着光伏容量占比的增加，广义短路比与临界广义短路比的差值增大，系统稳定裕度单调递增，说明多馈入直流系统中，在合适的控制方式下，光伏容量占比的增大可以提升系统的静态电压稳定性，提高受端电网强度。

5 结语

本文提出了包含光伏电站的多馈入直流受端电网的广义短路比及其临界值的计算方法，研究了光伏电站接入对多馈入直流受端电网强度的影响。研究表明，光伏电站接入的影响分为外特性交互作用和输出有功功率两方面，最终的综合影响结果是这两方面结果的叠加。在光伏的交流电压-无功功率下垂控制中，下垂控制系数K的选择至关重要，可以有针对性地确定最小下垂系数，以确保接入的光伏电站不会降低受端电网强度并恶化系统的稳定性。

本文考虑了直流电压控制和交流电压-无功功率下垂控制的光伏电站接入对多馈入直流受端电网静态电压稳定性的研究，但是有一定前提假设条件，未来将弱化这些假设条件，并研究更多运行工况和控制方式下的光伏电站控制策略和参数整定问题。

感谢国网浙江省电力有限公司科技项目“‘双高’电力系统电压支撑强度评估方法、指标及实用化计算方法”对本文研究工作的支持!

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。