基于实测应变的典型热防护结构位移场实时重构

胡明月 吴邵庆,2 董萼良,2

(1东南大学土木工程学院， 南京 210016)(2东南大学江苏省空天机械装备工程研究中心， 南京 2011189)

使役环境下的高速飞行器结构状态监测近年来成为研究的热点[1]，而形变监测是状态监测的重要组成部分.现有的测量手段难以直接对飞行器结构的形变进行长时间的实时监测.因此，发展测算融合型的形变测量方法，将有限点的响应测量与重构算法相结合进而重构出飞行器结构的位移场，成为一种重要的飞行器状态监测手段.

基于测算融合的结构位移场重构方法主要有2种：基于载荷识别[2-7]的重构方法和模态法[8].基于载荷识别的重构方法的思路是先利用部分测点处结构响应识别出结构上作用的真实载荷，并进一步将载荷作用于结构计算位移场，完成重构.由于载荷识别和位移场计算都需要一定时长，这类方法大多难以实现结构位移场的实时重构.模态法是基于模态叠加理论发展而来的一种位移场重构方法.通过实验或者有限元建模分析得到结构的应变模态矩阵和相应的位移模态矩阵，对这2个矩阵进行计算可以得到应变-位移转化矩阵，结合应变测量系统测得的结构应变场实现对结构位移场的重构.但是该算法的精度过度依赖于结构建模[9]和模态分析[10]的准确性且对应变传感器的布置方式提出了很高的要求.

相比测算融合型方法，插值重构型方法更适合结构位移场的实时重构，随着光纤应变测量技术的发展，插值重构型方法对测点数目较多的要求也容易获得满足.目前主流的插值重构算法有2种：逆有限元法[11-15]和基于Ko位移理论的方法.逆有限元法可以利用结构表面有限测点的应变信息重构出结构整体变形，包括挠度和转角，已经在一些航空航天结构上获得应用.基于Ko位移理论的方法原理简单，近年来在位移场重构方面也得到广泛的应用.2007年Ko等[16]正式提出了Ko位移理论，并将该理论应用于Ikhana无人机双锥形机翼变形的测量[17]，具有很高的重构精度.Jutte等[18]将Ko位移理论用于同时产生弯曲和扭转的机翼结构位移场重构，并运用光纤进行应变测量，通过实验结果发现弯曲变形重构误差会对扭转变形重构结果造成很大影响.Pak[19]对Ko位移理论进行进一步改进，从原来一次只能重构一个方向的变形到一次可以同时重构多个方向的变形，并将改进后的Ko位移理论与有限元模型相结合从而插值和外推出整个结构在所有方向上面的挠度和转角，利用该理论重构出的位移场计算结构加速度和速度[20].Esposito等[21]将Ko位移理论用于同时产生弯曲和扭转的复合材料翼盒的位移场重构.

传统Ko位移理论适用于固支边界条件下结构位移场重构.但在实际结构中，固支边界情况较为少见，使得该理论的应用范围受到限制，对于简支结构的位移场重构效果较差.本文拟对传统Ko位移理论进行改进，使得该方法可以适用于非固支工况，并将改进后的Ko位移理论用于典型热防护结构四点弯工况下的位移场重构.通过有限元仿真，验证基于Ko位移理论重构算法的准确性.以典型热防护结构为实验对象，设计并开展相关试验，验证重构算法的可靠性和重构位移场的精度，并进一步实现了典型热防护结构四点弯工况下重构位移场的实时显示.为非固支边界条件下结构位移场实时监测提供了一种间接测量的手段.

1 改进的Ko位移理论

Ko位移理论的主要思想是：在结构表面有限测点处布置应变片，根据应变片的布置对结构进行分段，每相邻2个应变片之间为一个小段.在该小段内推导应变与位移的关系，利用实测应变获取相关的位移场信息.再依次递推，预测出整体结构的位移场信息.

根据材料力学的基本假设，当简支梁结构的变形属于小变形时，可以忽略结构的轴向位移，即可以忽略轴向应变与轴向位移之间的线性关系.在小变形的前提下，欧拉-伯努利梁表面应变与梁弯曲变形后挠度之间的关系式[17]为

(1)

式中，ε(x)为应变；w为沿着y方向的挠度；y0为横截面处梁上表面到中心面的距离.

通过应变片可以测得第i段起始点xi处的应变εi和末尾点xi+1处的应变εi+1.可以假设梁在弯曲变形为主的情况下，表面应变呈线性分布，那么从第i段起始点到末尾点之间的应变信息就可以通过线性插值得到，即

(2)

在已知第i段起始点的坐标xi和斜率tanθi的情况下，通过对式(2)在[xi,xi+1]上进行一次积分可得到第i段的斜率方程tanθ(x)的具体表达式：

(3)

在已知第i段起始点处挠度wi的情况下，对式(3)进行一次积分可以得到挠度方程：

(4)

为了完成上述2次积分过程，需要知道第i段起始点的转角θi和挠度wi.根据连续性条件，第i段末尾点的转角和挠度等于第i+1段起始点的转角和挠度.因此，只需要知道第1段起始点的转角和挠度就可以重构出整个梁结构的挠度场.

第1段起始点的转角和挠度可根据边界条件得到.传统Ko位移理论假设结构是一端固支的，根据该假设，第1段起始点的转角和挠度都为0.此时第1段的斜率方程和转角方程表达式为

(5)

(6)

将式(2)代入式(5)、(6)即可求得第1段斜率和挠度方程；第1段末位点的斜率和挠度就是第2段起始点的斜率和挠度，以此类推就可以求出整个梁结构的挠曲线方程.

由传统Ko位移理论的假设可以看出，该理论只能用于至少一端固支梁结构的位移场重构.为了使得该理论可以用于简支结构的位移场重构，本文对该理论进行改进.

对于简支梁结构，支承端处挠度为0但是转角不为0.在小变形情况下，可以将简支梁变形进行分解，第1部分变形只表现为在简支梁结构支承端处产生转角；第2部分变形只表现为在简支梁结构上、下表面产生应变.假设在简支梁起始端处的转角为θ0，在第1段简支梁结构上第1部分变形导致的斜率和挠度的表达式分别为

tanθ(x)=-tanθ1x1≤x≤x2

(7)

w(x)=-tanθ1×(x-x1)x1≤x≤x2

(8)

在第1段简支梁结构第2部分变形对应的斜率表达式和挠度表达式分别为

(9)

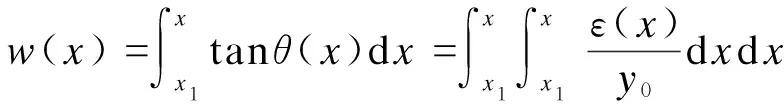
(10)

由于这2部分变形互不相关，将它们线性叠加就可得到第1段简支梁结构斜率和挠度表达式：

(11)

(12)

依次递推，能够得到第i段简支梁结构的斜率和转角表达式：

(13)

(14)

式(13)、(14)与式(3)、(4)不同之处在于存在2个未知数ε(x)和θ0.其中，ε(x)可以根据应变测点的布置和测得的应变值分段线性拟合.在对ε(x)进行分段拟合后，最后一段(假设为第n段)简支梁结构末位点的挠度值wn+1只包含1个未知数θ0.对于简支梁结构，在小变形情况下，支承端处轴向的位移可以忽略不计，竖向位移为0，等价于wn+1=0.根据该条件可以求出θ0，进而求出整个简支梁结构的挠度表达式.具体流程如图1所示.

图1 基于改进的Ko位移理论的重构流程

2 仿真校验

首先建立典型热防护结构有限元模型，施加载荷，计算结构参考位移场和应变场.然后设定应变信息提取点和重构区域，将提取出的应变信息代入重构算法获得重构区域重构位移场，利用参考位移场验证重构位移场的精度.

2.1 典型热防护结构和有限元模型

利用ABAQUS对热防护结构试验件进行有限元建模(见图2)，各部分几何尺寸如表1所示.胶层和底板材料参数如表2所示，面板和芯层材料参数如表3所示.

图2 典型热防护结构局部有限元模型

表1 典型热防护结构各部分几何尺寸 mm

表2 胶层和底板材料参数

表3 面板和芯层材料参数

典型热防护结构整体采用六面体单元建模，上面板、芯层、下面板、胶层和底板分别沿厚度方向划分为3、16、2、1和4层.整个有限元模型包含43 309个节点和37 920个单元.

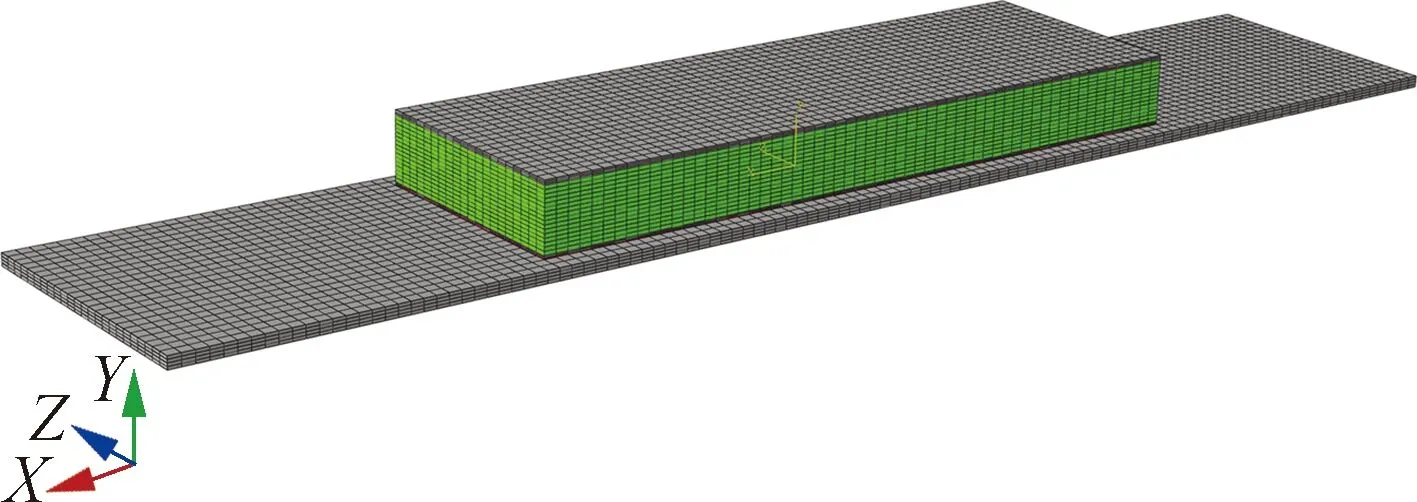
图3 典型热防护结构有限元模型

在底板设置应变测点，底板沿厚度方向被划分为4层，需要读取测点处对应上下表面节点处的应变值.底板单元节点划分、位移重构区域以及应变提取节点的位置如图4所示.

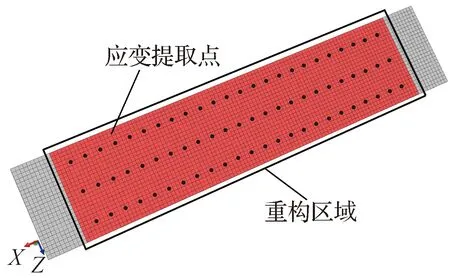
图4 位移重构区域和应变提取点布置

2.2 重构位移场精度验证

读取图4所示应变提取点处的应变信息，利用重构算法重构区域内的位移场，并与ABAQUS有限元软件计算出的参考位移场作对比.图5给出了参考位移场和重构位移场.

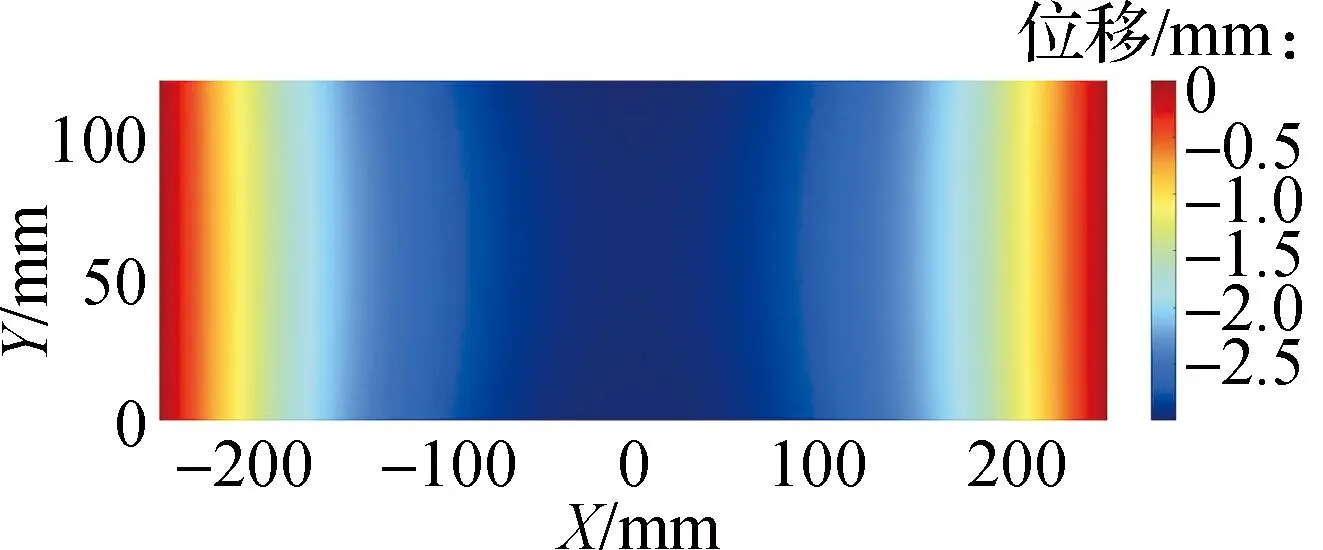
(a) 参考位移场

(b) 重构位移场

图6是重构区域节点相对误差图，由图可知，基于改进Ko位移理论重构出的典型热防护结构金属底板位移场具有很高的精度.重构区域节点最大相对误差为1.712%，平均相对误差为1.080%.

图6 重构区域节点相对误差图

3 四点弯试验验证与重构位移场实时演示

3.1 位移场重构试验与实时演示系统

典型热防护结构分布式光纤光栅布置和位移测点布置如图7所示.典型热防护结构试验件位移场重构试验系统如图8所示，该试验系统由加载系统、位移测量系统、光纤测量系统和实时演示系统4部分组成.加载系统由四点弯工装和MTS万能试验机组成，将试验件固定在四点弯工装上，通过MTS万能试验机施加荷载.位移测量系统由3个位移计组成，用于测量位移测点的实际位移值.光纤测量系统由解调仪、分布式光纤光栅和网线组成，用于读取每个光纤测点的应变信息.实时演示系统利用实时读取的应变信息实现位移场的实时重构.试验件的尺寸、材料参数与加载位置等与仿真工况一致.

图7 分布式光纤光栅和位移测点布置(单位：mm)

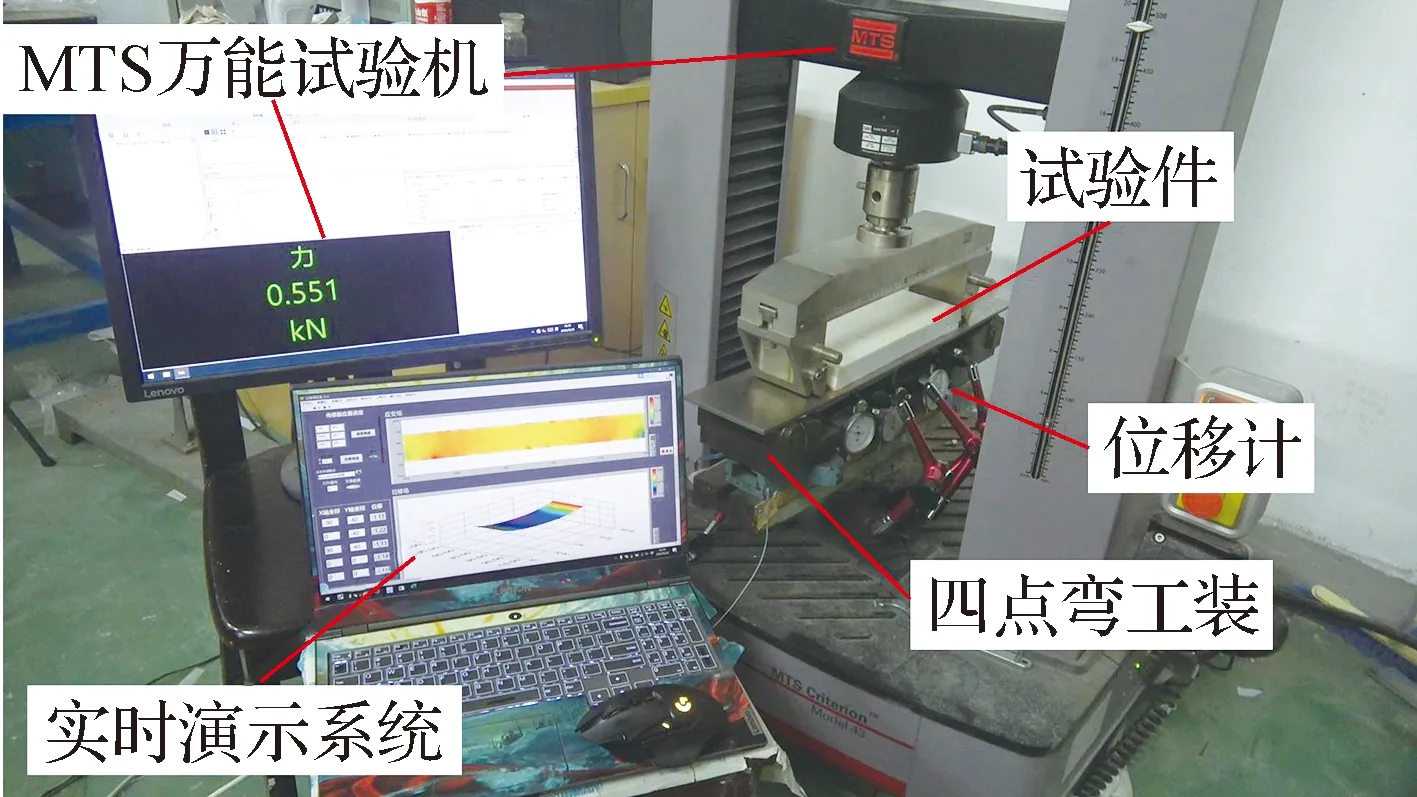
图8 位移场重构试验系统

在试验前对TPS结构进行有限元仿真，并计算该结构在四点弯工况下应变云图，根据应变云图决定试验过程中光纤布局形式.在试验过程中，将图8中所示光纤划分为3段，每段提取57组光纤数据，每组数据间隔7.9 mm，总计提取171组光纤应变数据.

实时演示系统的界面由4部分组成：传感器定位与校零窗口、应变数据采集和存储文件路径设置窗口、重构应变显示窗口和重构位移显示窗口以及位移读取窗口.传感器定位与校零窗口主要功能是通过输入每段光纤光栅起始和末尾点的编号实现测点编号与坐标信息的一一对应，并通过数据处理实现校零；应变数据采集和存储文件路径设置窗口是用来控制是否存储应变信息并设置应变信息存储位置；重构应变显示窗口和重构位移显示窗口是显示重构应变场二维云图和重构位移场三维云图；位移读取窗口可以通过输入节点几何坐标实时读取该节点的位移信息.

3.2 四点弯工况下典型热防护结构底板位移场重构

对典型热防护结构进行四点弯加载试验，利用分布式光纤光栅测得的应变数据进行典型热防护结构金属底板位移场重构，并与实际测得的位移数据进行对比.

3.2.1 900 N荷载工况下底板位移场重构效果

对典型热防护结构试验件预压100 N，分级加载至900 N后记录该时刻的应变数据，代入重构算法进行全场位移重构.同时测量图7所示位移测点处的实际位移数据，并与对应的重构结果作对比，加卸载2次，对比结果如图9所示.

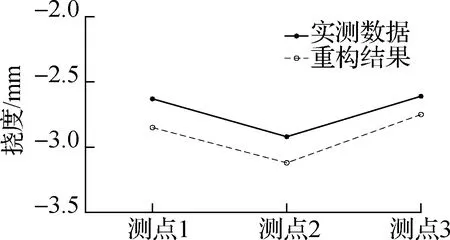
(a) 第1次加载实测数据与重构结果

(b) 第2次加载实测数据与重构结果

(c) 实测数据与重构结果相对误差

单载荷工况下，在位移测点处重构数据与实际数据之间的相对误差低于10%.

3.2.2 分级加载工况下底板位移场重构效果

对TPS试验件进行第1次分级加载：预压250 N，进行分级加载，每一级加载100 N，加载到650 N后直接卸载到450 N后停止卸载.记录分级加载及卸载过程中每一级的应变数据，代入重构算法进行全场位移重构.同时测量图7所示位移测点处的实际位移数据，并与对应的重构结果作对比，对比结果如图10所示.

(a) 测点1的实测数据与重构结果

(b) 测点2的实测数据与重构结果

(c) 测点3的实测数据与重构结果

(d) 实测数据与重构结果相对误差

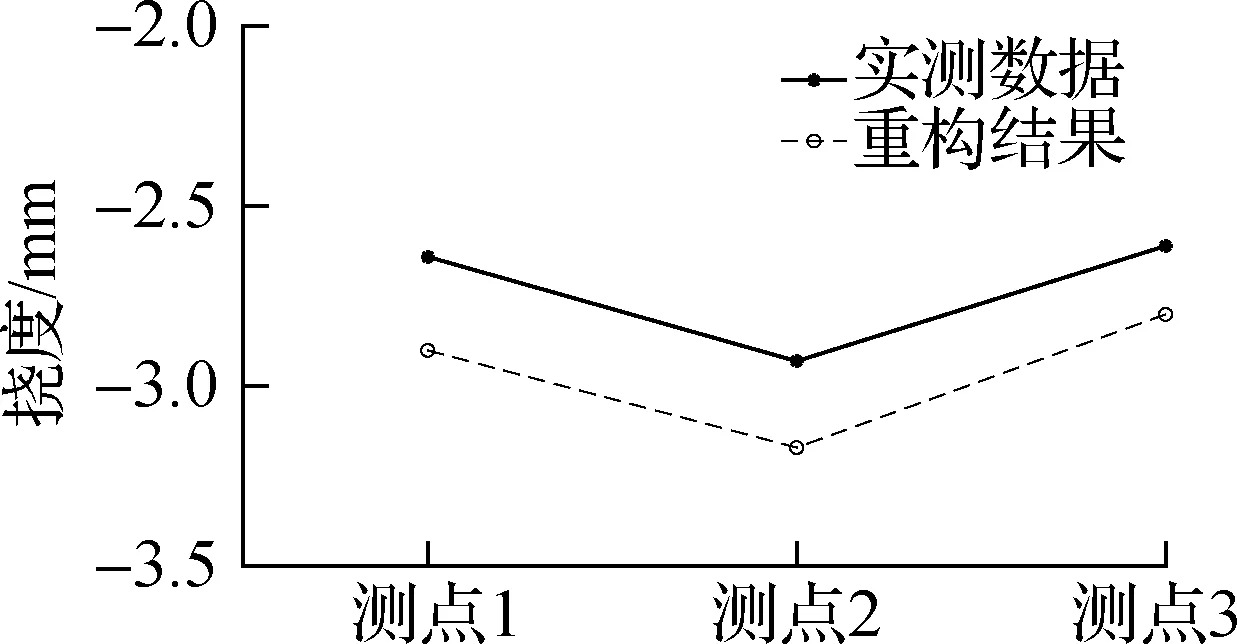
对TPS试验件进行第2次分级加载：预压250 N，进行分级加载，每一级加载100 N，加载到850 N后进行分级卸载，每一级卸载200 N，卸载到450 N后停止卸载.记录分级加、卸载过程中每一级的应变数据，代入重构算法进行全场位移重构.同时测量图7所示位移测点处的实际位移数据，并与对应的重构结果作对比，对比结果如图11所示.

由结果可知，在分级加载的变载荷工况下，位移测点处重构数据与实际数据之间的相对误差低于10%；并且重构数据是通过实时重构系统实时读取获得的.这说明对于实际结构分级加载工况下，基于改进Ko位移理论实时重构出的位移场具有较高的精度和稳定性，而且针对变载荷具有较好的跟踪能力.

(a) 测点1的实测数据与重构结果

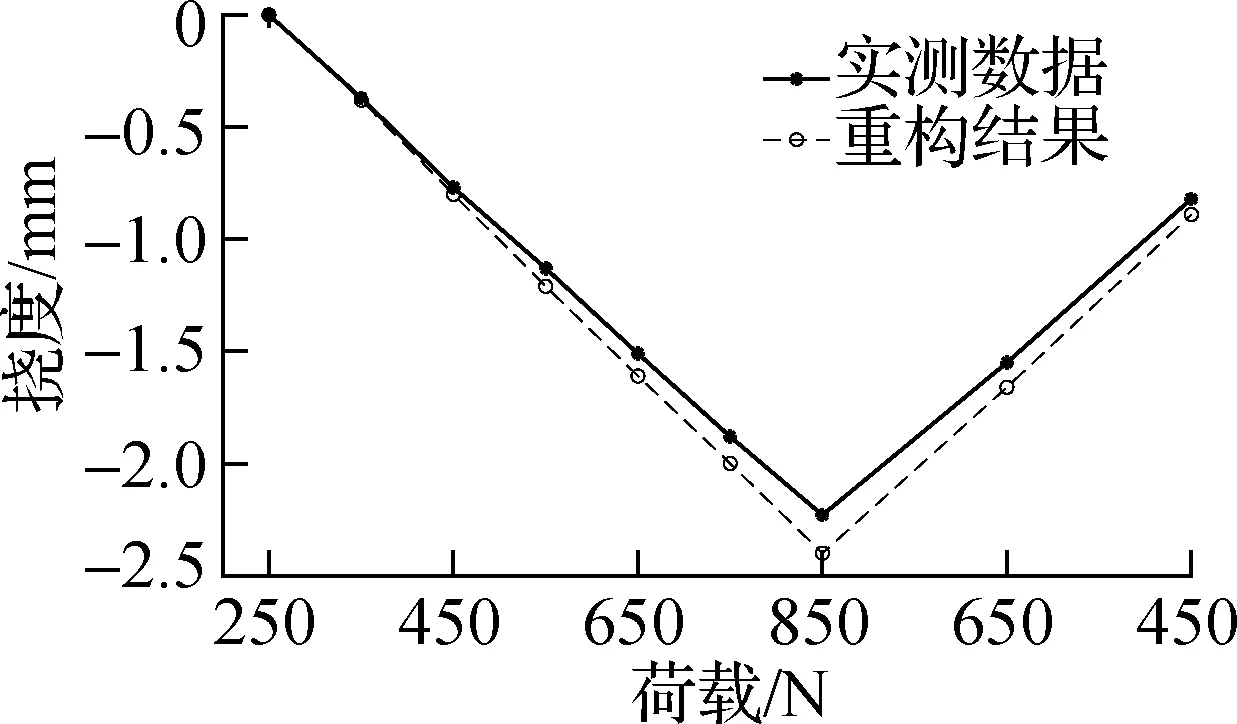
(b) 测点2的实测数据与重构结果

(c) 测点3的实测数据与重构结果

(d) 实测数据与重构结果相对误差

在试验过程中，部分试验结果不太理想，重构误差接近10%.具体原因和改进措施如下：

1) 光纤在应变测量过程中受环境影响产生扰动，测量的应变数据包含噪声是重构误差的主要来源之一，当载荷引起的应变量级较低时尤其显著；可以通过适当提高加载量级的方法提高测量应变数据的信噪比来降低环境噪声的影响.

2) 光纤在粘贴过程中无法保证完全沿着板长方向布置，并且光纤与底板间的胶层较厚，粘贴的偏差将引起实测应变数据大于真实应变数据，造成重构位移数据偏大，可以通过提高光纤粘贴精度来提高测量数据的精度，减小位移场重构误差.

3) 基于Ko位移理论的重构算法在进行重构计算时，需要代入结构上、下表面对应点处的应变信息计算结构中性面位置.由于技术手段的限制，现阶段无法在气凝胶与底板之间粘贴光纤或其他应变传感器，因此只能利用仿真得到的底板中性面位置信息进行重构.但有限元模型与实际模型存在一定的差异，仿真得到的底板中性面位置低于实际试验过程中底板中性面位置，造成重构结果一直偏大.

4) 在试验过程中，由于试验工装并非绝对水平，使得试验件出现一端高一端低的情况，但在重构过程中认为试验件处于水平状态，造成重构结果一直偏大；可以通过提高试验工装精度，保证工装绝对水平从而减小位移场重构误差.

4 结论

1) 基于传统Ko位移理论，发展了适用于简支边界条件的改进Ko位移理论，实现基于实测应变信息对简支结构位移场进行重构.

2) 通过商用有限元软件建立典型热防护结构试验件四点弯工况下的有限元模型，利用读取预设应变测点所在单元的应变信息实现了基于改进Ko位移理论的位移场重构算法的仿真验证，说明改进后的重构算法具有较高的重构精度.

3) 开展热防护结构试验件的四点弯试验，利用结构底板表面粘贴的分布式光纤光栅获取的实测应变信号开展底板位移场重构，并利用位移计读取的实测位移验证算法的精度.结果表明：基于改进Ko位移理论实时重构出的位移场具有较高的精度和稳定性，且对变载荷具有较好的跟踪能力；测量环境噪声、光纤粘贴精度、测点排布等都会对重构结果产生影响，有待进一步研究.

4) 该方法中位移场与测量的应变数据是一一对应的，本文的方法适用于振动激励下的结构位移场重构.