基于子动作特征矩阵与DTW算法的手臂动作识别方法
2021-08-07崔建伟曹尔凡陆普东李志钢
崔建伟 曹尔凡 陆普东 李志钢
(东南大学仪器科学与工程学院, 南京 210096)
助残机械假手可以在一定程度上代替人手帮助残疾者进行生活自理[1].但是大多数假手产品只能被动模拟人手功能,通过按钮、语音等人为信号控制机械假手完成抓握动作,操作繁琐,给残疾者造成心理负担.人的手臂是助残手的牵引工具,准确识别手臂动作,将动作特征反馈给假手系统,由其学习并调整参数,对实现假手的智能化控制具有一定意义.基于惯性测量单元(IMU)的手臂动作识别是人体动作识别领域的热点.
IMU是在MEMS技术的基础上将加速度计、角速度计、磁力计等多种微器件集成的惯性组合,具有微型化、低功耗、低成本等优势[2].Wang等[3]在老年人手腕部位佩戴IMU并结合环境传感器,采用支持向量机模型对17种日常人体活动进行识别,总识别率达到96.82%;Mazomenos等[4]在受试者的肘部、腕部分别佩戴IMU,通过对手臂运动过程中的关节角、关节位置变化进行分析,采用阈值区分法对倒茶动作的多个子动作进行区分,取得良好的分类效果.
动态时间规整(DTW)算法是一种模板匹配算法,用来计算时间序列数据之间的相似性.由于该算法对连续时间序列数据有很好的处理效果,且相对于机器学习和神经网络算法具有数据需求量小、计算量小的优势[5],目前在基于惯性器件的动作识别场景也有较多应用[6-7].Lian等[8]在运动员的大臂和小臂分别穿戴IMU,使用与DTW原理相同的LCS算法对棒球投掷动作的6个子动作进行识别,平均识别率达到95.14%;刘盛羽[9]将决策树算法与DTW算法相结合,基于IMU和压力传感器对人体步态动作进行分类,整体识别率达到95%以上.
上述研究都使用了DTW算法直接处理人体动作的IMU时间序列数据,虽然取得了良好的识别准确性,但仍存在不足:①DTW算法的耗时与时间序列长度相关.动作持续时间越长,算法的耗时越大,识别的实时性受很大影响.如持续时长超过10 s的动作,识别的耗时会超过4 s,在实时性要求较高的助残手系统中不被允许.②不同的人做同一个动作的速度可能会有很大差别,对2个持续时间差异较大动作的时间序列直接进行比较计算,识别效果会变差.针对以上不足,本文提出基于子动作特征矩阵的DTW算法对手臂动作数据进行处理.不同于直接计算时间序列数据,本文设计了一种活跃波形匹配算法,将手臂动作按照执行的顺序拆解成若干个子动作,对每个子动作计算角速度和手臂空间位置变化的若干组特征值,构成特征向量.然后将完整手臂动作的所有子动作特征向量进行组合,构造子动作特征矩阵,在识别阶段用子动作特征矩阵代替时间序列进行模板匹配计算.该方法使得基于DTW算法的手臂动作识别不受动作持续时间长度的影响,提高了识别的准确度和实时性.最后将本文提出的方法与常见的直接计算时间序列数据的方法进行比较,验证了该方法的有效性.
1 识别系统整体框架
本文使用数据手套作为手臂动作数据采集平台.数据手套由3个IMU和5个弯曲传感器组成.每个IMU集成了三轴加速度计、三轴角速度计、三轴磁力计,同时内置了DMP姿态融合器,可直接输出四元数和姿态角数据.本系统中,3个IMU分别固定在右手手臂的大臂、小臂和手背的中间位置,且3个IMU的佩戴方向一致,以便于后文解算手臂末端空间位置.
如图1所示,U-XUYUZU、F-XFYFZF、H-XHYHZH分别为3个IMU的载体坐标系,Y沿手臂指向前方,Z垂直于Y指向外侧,X垂直于YZ平面指向后方.

图1 IMU佩戴位置与载体坐标系方向
手臂动作识别的整体流程如图2所示,共包含空间位置解算、子动作拆解、构造特征矩阵、制作动作模板、动作识别5个步骤.

图2 手臂动作识别流程
2 手臂空间位置解算
从骨骼构造的角度看,手臂是一个简单的连杆模型,肩部为固定点,大臂、小臂、手掌在肘关节和腕关节的连接下可相对运动.本文以手臂连杆模型为基础,参照机器人的正向运动学理论对手臂末端的相对空间位置进行解算.
图3为右手手臂连杆模型示意图.O-XOYOZO、A-XAYAZA、B-XBYBZB、C-XCYCZC、D-XDYDZD分别为胸坐标系、肩关节坐标系、肘关节坐标系、腕关节坐标系、掌关节坐标系,LOA、LAB、LBC、LCD分别为半肩宽长度、大臂长度、小臂长度、手掌长度.因胸部与肩部未佩戴IMU,无法测量2个部位的姿态,故本文设定胸坐标系与肩坐标系为固定坐标系,即O-XOYOZO与A-XAYAZA固定不动,且2个坐标系在同一水平面上,与地理坐标系方向一致;B-XBYBZB、C-XCYCZC、D-XDYDZD方向分别与大臂IMU、小臂IMU、手背IMU载体坐标系方向一致.本文的手臂空间位置解算以O-XOYOZO为基准坐标系,以D-XDYDZD的原点D为手臂末端位置解算对象.

图3 右手手臂连杆模型
求点D在O-XOYOZO下的坐标是一个坐标系连续变换的过程.以单个坐标系变换O-XOYOZO到A-XAYAZA为例,点A在O-XOYOZO下的坐标求解公式为
(1)
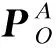
(2)

从O-XOYOZO到D-XDYDZD经历了4次坐标系变换,根据正运动学理论,只要分别求出4次变换的齐次变换矩阵,依次相乘,即可求出点D在O-XOYOZO下的坐标:
(3)
求解过程中,关节坐标系之间的旋转角度为前后时刻位置节点的IMU所测姿态角差值,是一个相对角度,因此IMU佩戴位置的差异不会影响手臂末端位置的解算准确性,解算方法的鲁棒性较好.同时,每个人的手臂长度不同,为了简化计算,本文依照国家标准《中国成年人人体尺寸》[11]中的人体尺寸参数,统一手臂模型长度参数,取LOA=18.75 cm、LAB=31.30 cm、LBC=23.70 cm、LCD=10.00 cm,手臂总长65.00 cm.
图4展示了在手臂画半圆动作下,该方法解算的手臂空间轨迹与理论轨迹的对比,其中动作的起点为(18.75,0,-65) cm,终点为(18.75,0,65) cm.从图中可以看出二者基本吻合,验证了正运动学解算手臂位置的正确性.

图4 手臂空间位置解算方法验证
3 子动作拆解和子动作特征矩阵
日常生活中,一个复杂的连续手臂动作可以按先后顺序拆解成若干个子动作.例如当我们喝水时,通常是按照伸手拿杯子—将杯子送到嘴边—放回杯子—将手放回的子动作顺序完成动作.在自然状态下,人不可能匀速完成整个动作,子动作之间会产生短暂的停顿.利用这个特点,本文采用拆解子动作并构造子动作特征矩阵的方式来研究手臂动作.假设一个完整手臂动作的子动作数量为n个,那么该动作的子动作特征矩阵为S=[F1F2…Fi…Fn],其中Fi为第i个子动作的特征向量,包含了能描述该子动作的若干个特征值.在识别阶段,使用子动作特征矩阵代替长度较大的时间序列,作为DTW算法的输入进行动作相似度比较,可提高识别的准确性与实时性.
在构造子动作特征矩阵之前,需要通过对原始动作数据进行分析,总结运动规律,从而将子动作拆解出来.对于IMU数据,常见的方法是选取加速度进行时域或频域分析[12].考虑到手臂是一种连杆模型,手臂运动的本质就是旋转,因此角速度能很好地表征手臂运动信息.本文选取手背部位的角速度进行分析.
3.1 数据预处理
设置数据采集的频率为50 Hz,首先对原始数据进行预处理.
3.1.1 滤波
采用一阶低通滤波器对原始数据进行滤波,去除高频噪声,即
(4)
式中,Yk为本次滤波输出值;Yk-1为上次滤波输出值;Xk为本次采样值;α为滤波系数,取α=0.25.图5为滤波效果.
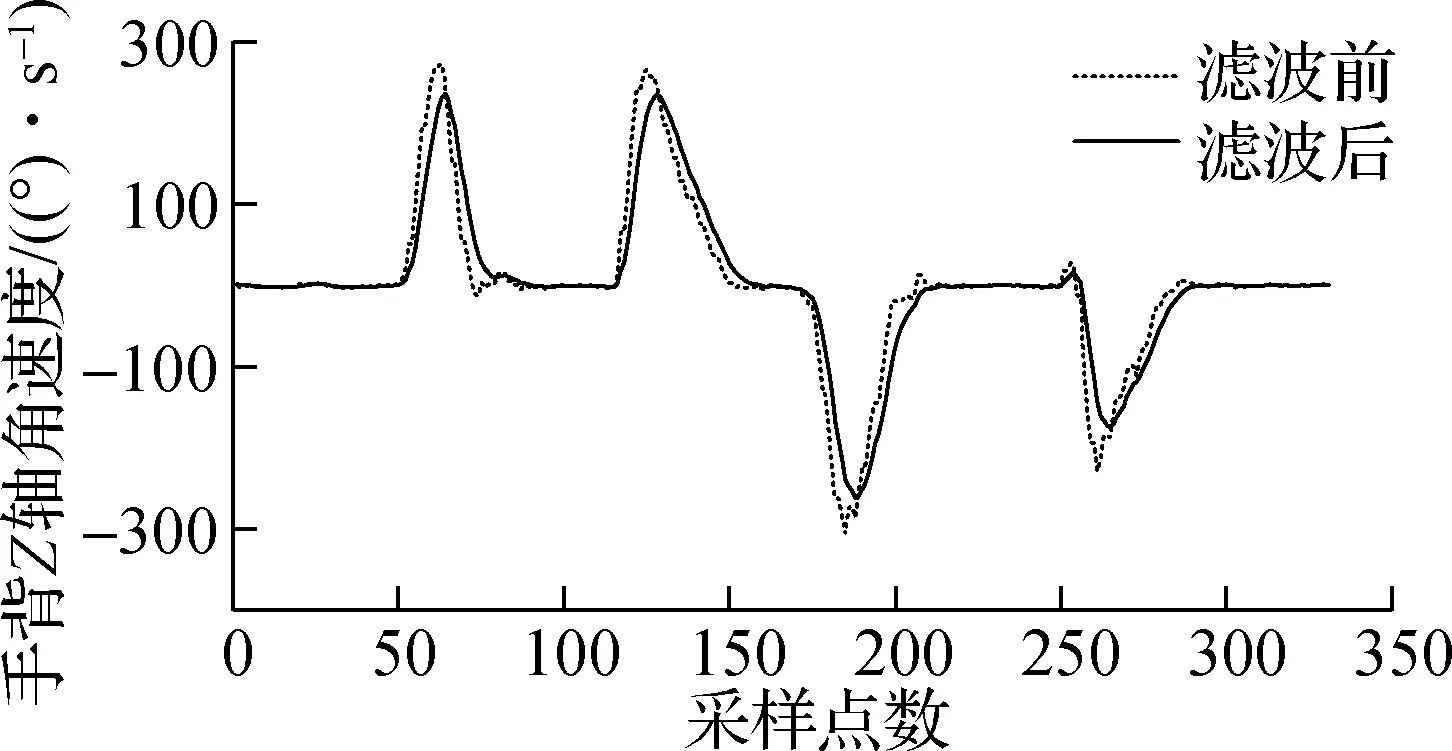
图5 一阶低通滤波前后对比
3.1.2 动作分割
对于采集的整段动作数据,需要从中分割出有效的数据段,这样更有利于特征的提取.常见的方法是设置固定长度的窗口,通过定长滑动分割出动作段,这种方法计算量小,但很容易将一个完整动作切割开,分割成功率低[13].基于第2节解算出的手臂空间位置可知,当手臂从静止开始移动或移动到静止时,手臂位置坐标会产生大幅变化,而差分值与方差对数据的剧烈变化较为敏感,因此从这2种特征量入手,来判断动作的始终点,分割出有效动作段.具体过程如下:
①设置滑动窗口长度w=10个采样点,窗口滑动步长l=1个采样点.
②对每个滑动窗口计算手臂位置三轴坐标差分值的和,即
(5)
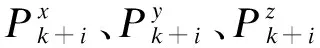
③对每个滑动窗口计算手臂位置三轴坐标的方差和,即
Vk=
(6)
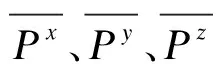
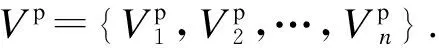
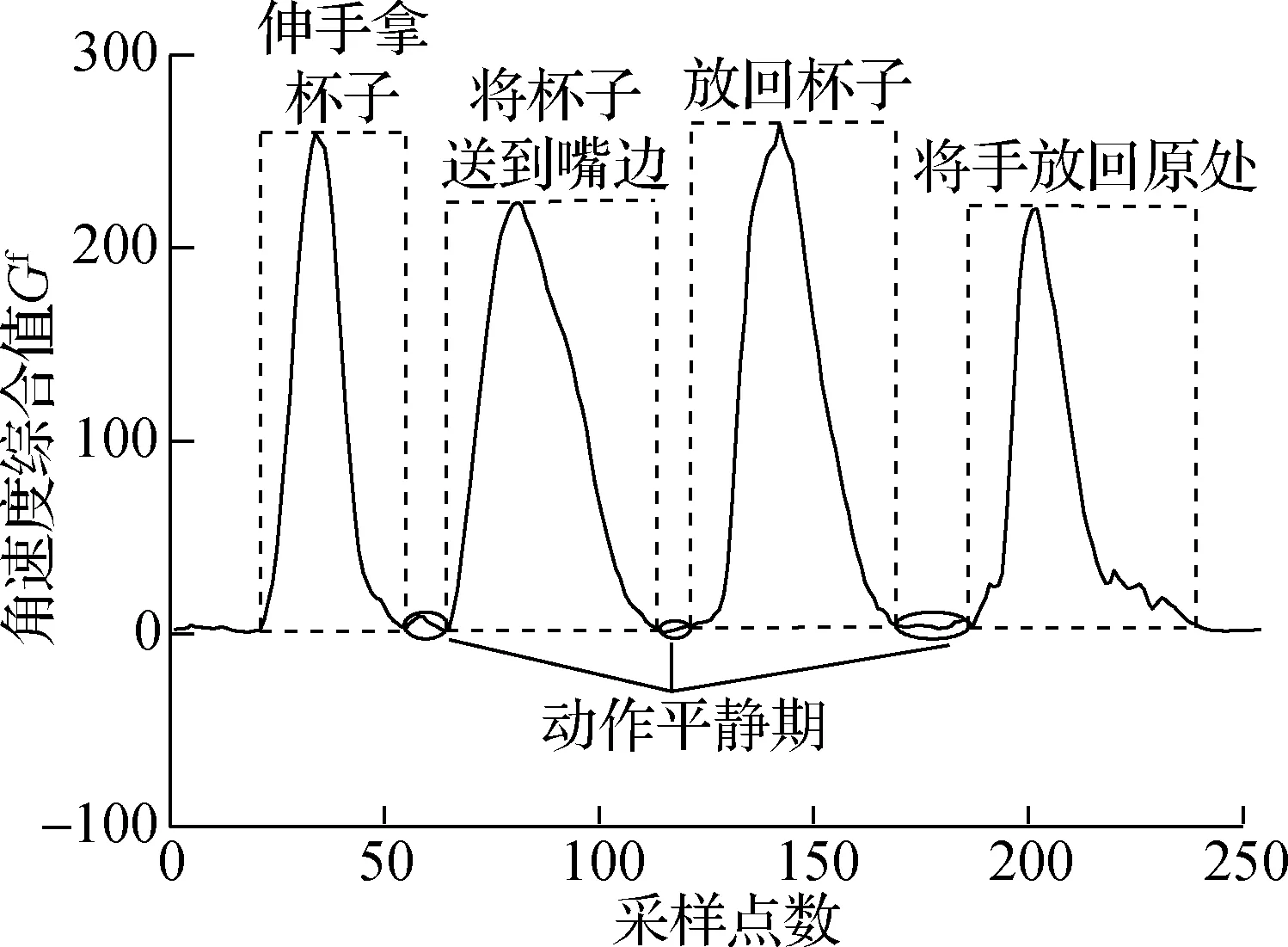
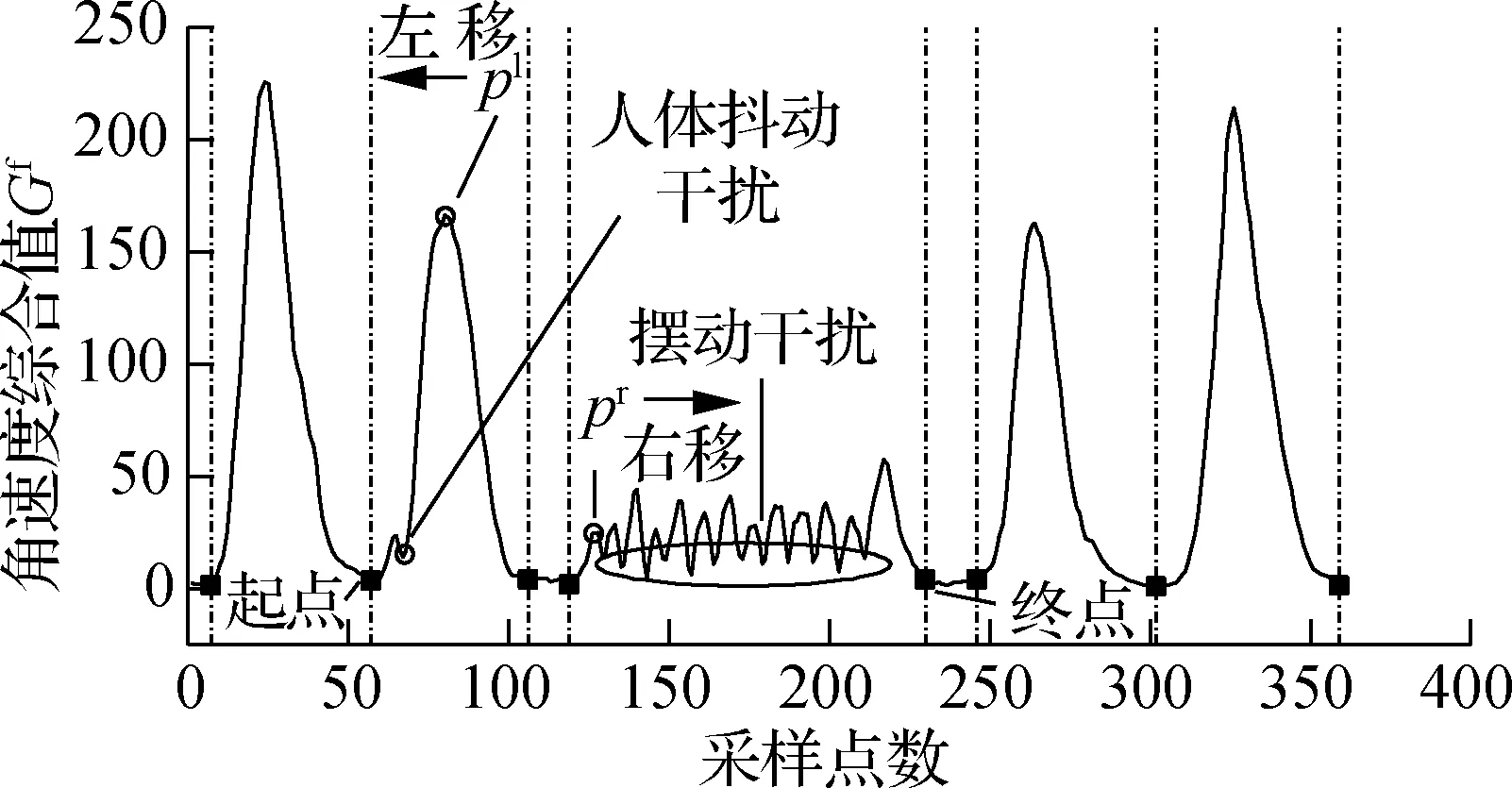
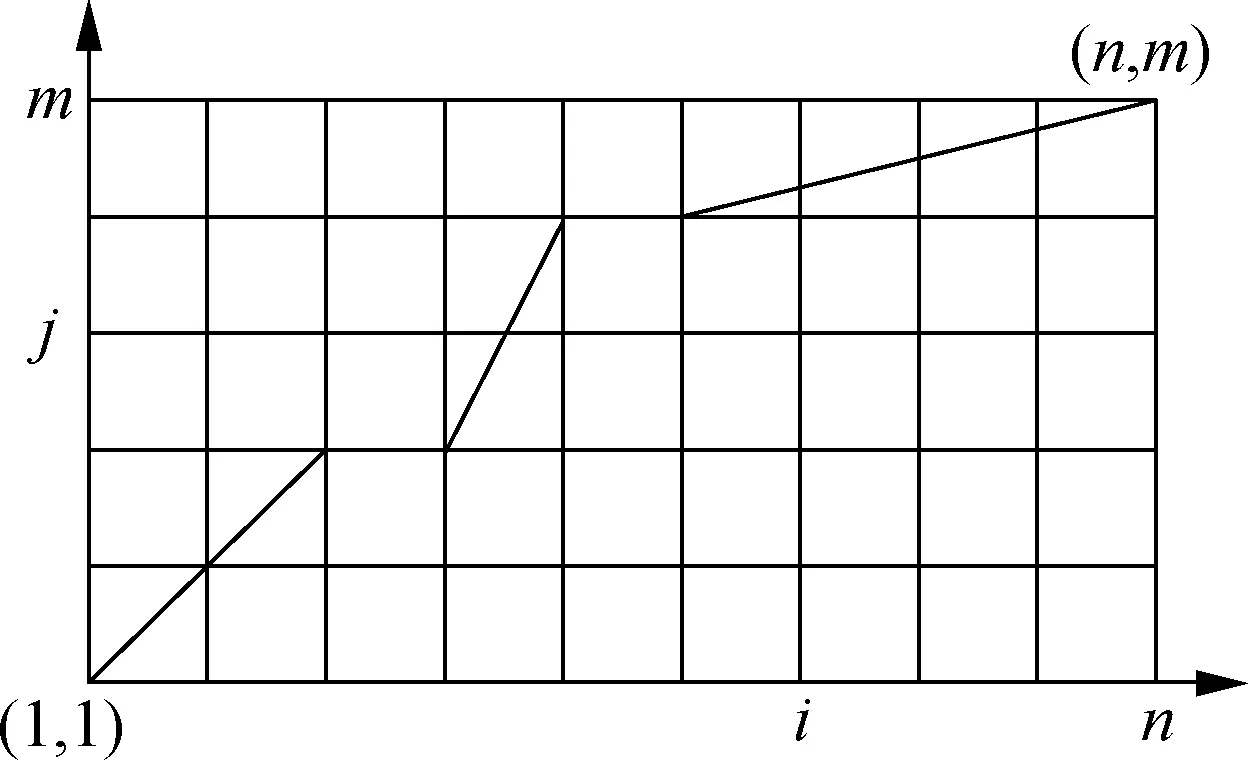
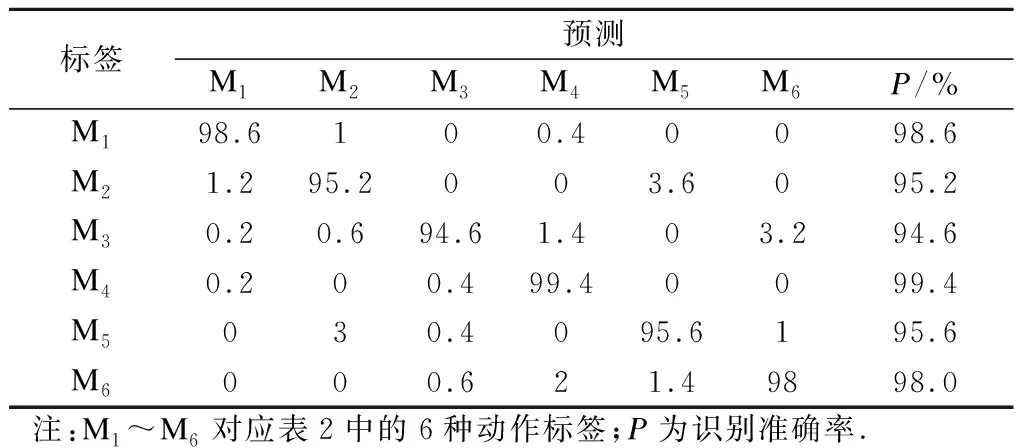
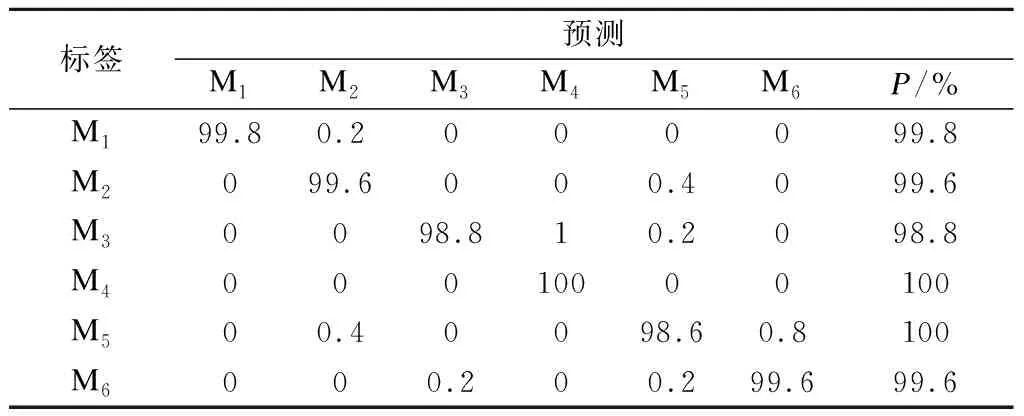
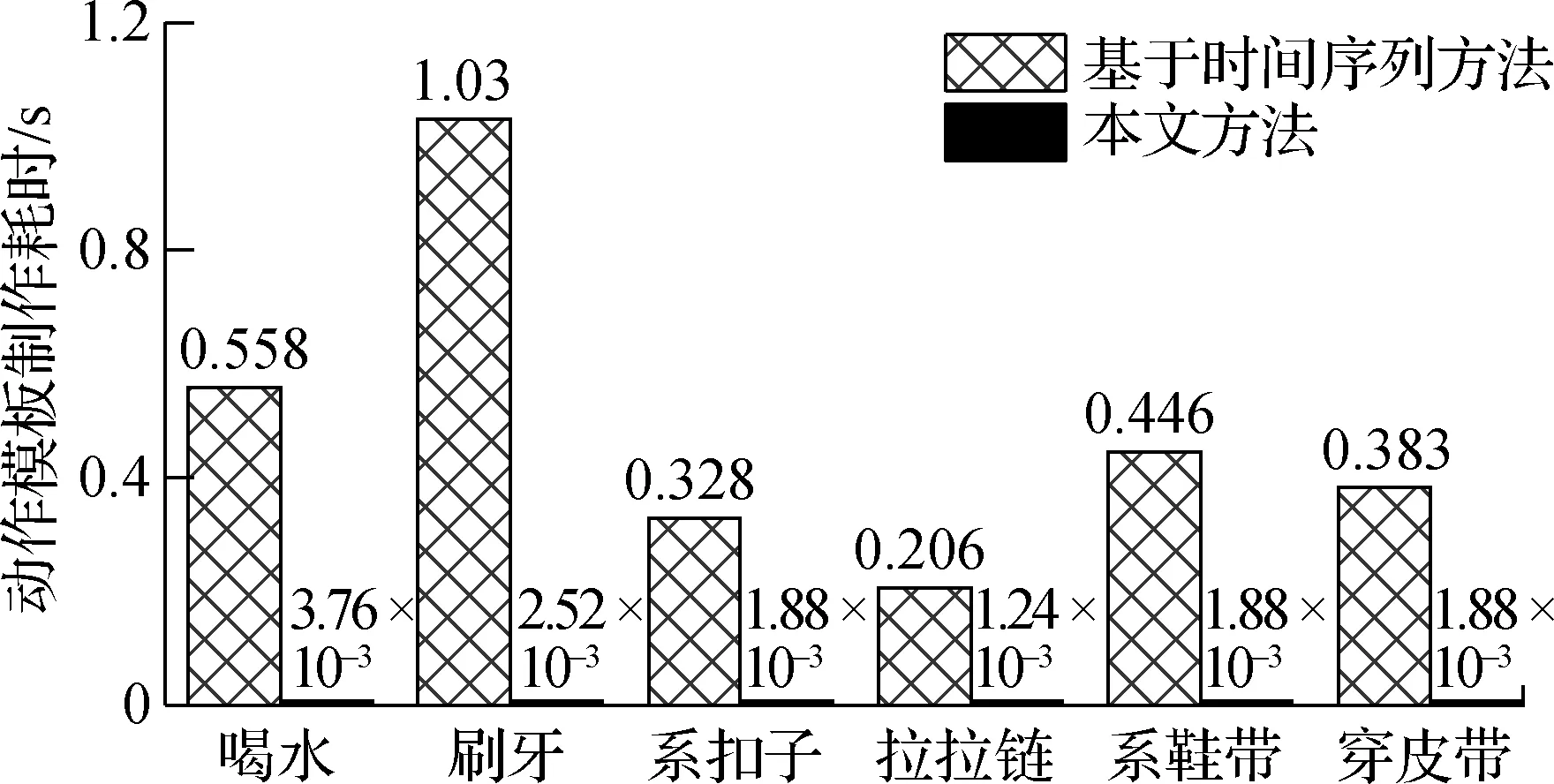
⑤寻找动作段起点,以喝水动作为例,如图6所示.对Vp中的元素遍历.若当前Vp值的横坐标对应的差分和E>tE,则该Vp值是与起点匹配的波峰,对当前采样点减去窗口长度偏移值ms,即找到起点,其中tE为大量实验后设置的E阈值.若E ⑥寻找动作段终点,从后向前遍历Vp,判断方法与步骤⑤相似.图6中,me为终点的窗口长度偏移值,对找到的Vp对应采样点加上me,即找到终点,设定me=3w. 图6 喝水动作分割 为了便于分析子动作拆解过程,计算手背部位角速度三轴分量的综合值,即 (7) 式中,Gx、Gy、Gz分别为手背角速度三轴分量.综合值Gf将三轴角速度融合,能够体现角速度的整体变化趋势. 以喝水动作的Gf曲线为例,分析手臂动作的规律.如图7所示,Gf出现了4个较大幅度的活跃波形,对应喝水动作的4个子动作,而每个活跃波形之间存在一个短暂的平静期,对应子动作之间短暂的停顿. 喝水动作的4个子动作都是手臂的单方向运动,而在日常生活中,手臂的来回摆动也是常见动作类型,例如刷牙、切菜等.图8是刷牙动作的Gf曲线.当实验者手拿牙刷做出来回摆动的刷牙动作时,Gf值对应的是一个频率较快的有多个波峰的波形,且手摆动的次数与波峰的数量相同.由于摆动动作频率高,且每次摆动代表的动作含义相同,本文将这种摆动动作视为一个子动作处理. 图7 喝水动作的活跃波形与子动作对应关系 图8 刷牙中的摆动动作Gf曲线 基于以上对手臂动作特点的分析,本文设计了一种针对动作Gf曲线的活跃波形匹配算法.该算法从区分Gf曲线的活跃期和平静期入手,匹配活跃期的起点与终点,将每个子动作对应的活跃波形从完整动作波形中摘取出,形成子动作窗口,完成子动作拆解.对于摆动类型子动作活跃波形,该算法也能准确匹配. 本文以图8的刷牙Gf曲线为例,简述活跃波形匹配算法的流程. ②遍历Gf,p,对每个波峰进行始点、终点探测.设置指针pl从当前波峰开始向左移动,每当遇到波谷时,判断波谷值Gf,v是否小于tg及波谷往前5个采样点的值是否都小于tg.同时满足这2个条件时,认为波形已进入平静期,该波谷则为起点,结束探测.若有一个条件不满足,则认为波形仍处于活跃状态,而该波谷是人体抖动或摆动动作导致的干扰点,忽略并让pl继续左移. ③探测活跃波形终点.设置指针pr从当前波峰开始向右移动寻找终点,方法与步骤②相同. ④对Gf,p中下一个波峰进行探测前,判断该波峰的横坐标值是否小于上一个活跃波形的终点.若满足小于条件,代表该波峰属于摆动动作的一个部分,已经被上一个子动作包含,不必再处理;若不满足条件,说明该波峰属于新的子动作,回到步骤②继续计算. 匹配的大致过程和结果如图9所示,图中的虚线为算法匹配出的子动作窗口边界. 图9 活跃波形匹配过程 子动作拆分完成后,需要对每个子动作窗口计算易于区分不同手臂动作的特征值.经过实验观察,选取6种特征值,如表1所示.其中,前3种描述了角速度变化特征,后3种描述了手臂空间位置变化特征. 表1 对子动作选取的特征值 将选取的6种特征值组成子动作的特征向量,即 F={ΔT,M,N, ΔPx, ΔPy, ΔPz}T (8) 然后将整个手臂动作的多个子动作的特征向量进行组合,得到手臂动作的子动作特征矩阵,即 S=[F1F2…Fi…Fn]T (9) 子动作特征矩阵S的构造使得手臂动作原本长度为几百甚至几千的时间序列,浓缩成长度为子动作数量的子动作特征矩阵,对于下文使用DTW算法识别手臂动作有重要的意义. DTW算法用来计算序列之间的相似性,是一种模板匹配算法,其原理如图10所示.相似性通常是用2个序列之间的最短距离γ来衡量.γ越小,2个序列的相似度越高.DTW算法应用于手臂动作识别的过程如下:建立动作模板库,将测试动作与所有模板动作进行比对,计算二者之间的最短距离γ,结果最小的模板动作即为识别结果. 图10 DTW算法原理 由于输入DTW算法中的2个序列长度通常不相等,不能直接计算它们之间的欧氏距离,因此使用动态规划的方法来计算. 以长度n的序列Q1={a1,a2,…,an}为横轴,长度m的序列Q2={b1,b2,…,bn}为纵轴,构造n×m的网格矩阵,网格中任意一个交叉点(i,j)为序列中的元素Q1(i)与Q2(j)的相交.网格中任意点(i,j)的最短距离γ的计算公式如下: (10) 式中,d(i,j)为Q1的第i个元素与Q2的第j个元素的距离,一般用欧式距离计算.以点(1,1)为起点,迭代计算至终点(n,m),γ(n,m)即为Q1和Q2最短距离的计算结果. 本文将构造好的子动作特征矩阵S代替序列Q输入到DTW算法中,S中的每列为特征向量,因此欧式距离d(i,j)的计算公式为 (11) 式中,S1(i,k)为特征矩阵S1的第i个子动作特征向量的第k个特征值;S2(j,k)为特征矩阵S2的第j个子动作特征向量的第k个特征值;l为特征值数量,即为6. 常见的模板匹配方法是将待识别动作序列与模板库中每一个模板动作序列进行比对,得出结果.这种方法会受到模板库规模的影响,模板库中模板数量越多,计算量就越大,耗时越久.为了减少计算时间,采取对每一类动作的所有模板动作序列求平均序列的方法,制作每类动作唯一动作模板,从而在识别阶段计算一次即可. 本文采用文献[14]中基于动态时间规整的重心平均(DTW barycenter averaging, DBA)算法对多个动作模板求平均模板.该方法通过反复迭代计算,减小临时平均模板与各个原始动作模板的最短距离γ,得到最终的动作平均模板,且不受迭代顺序的影响. 结合助残机械手的研究背景,选取了6种生活中常见的需要用手进行抓取的手臂动作,并定义了子动作顺序,作为测试本文方法的动作标签,如表2所示. 表2 实验选取的动作 寻找了10名健康受试者进行手臂动作实验,共8男2女,年龄23~50岁,身高160~185 cm.要求受试者的右臂佩戴数据手套,躯干保持不动,以自然状态与速度按照表2的子动作顺序执行手臂动作,每类手臂动作执行15次,最后采集得到900组动作数据. 从每个受试者执行的每类15组动作中,随机抽取5组作为模板组,其余10组作为测试组,共得到300组模板组数据,600组测试组数据.模板组每类动作为50组数据,对这50组数据使用DBA算法,得到最终的动作模板,共得到6个动作模板.同时,对数据集采用五折交叉验证,减少实验结果的随机性. 对采集的实验数据使用传统的基于时间序列的DTW方法和本文提出的基于子动作特征矩阵的DTW方法进行识别,并对2种方法的准确性和实时性进行对比.表3和表4分别是2种方法的识别结果混淆矩阵,表中数据为五次交叉验证取平均值的结果. 表3 基于时间序列的动作识别混淆矩阵 表4 基于子动作特征矩阵的动作识别混淆矩阵 通过观察表3和表4可知,本文方法相对于传统基于时间序列的方法准确性有所提高,总识别率由96.9%提高到99.4%,也证明了所选的6种子动作特征值对于区分不同动作有一定贡献. 图11(a)为每类动作50个模板样本的动作模板制作平均耗时对比,图11(b)为100个测试样本的动作识别平均耗时对比.可看出,无论是模板制作阶段还是识别阶段,基于子动作特征矩阵的方法耗时都小于基于时间序列的方法.进一步观察图11,发现基于时间序列的方法识别耗时与动作的持续时间成正相关,而基于子动作特征矩阵的方法识别耗时差距很小,与动作的持续时间长短无关,证明了本文提出的识别方法具有良好的实时性. (a) 动作模板制作耗时 (b) 动作识别耗时 1) 设计了手臂动作识别流程,包含手臂空间位置解算、子动作拆解、子动作特征矩阵构造、动作模板制作、动作识别等5个步骤. 2) 针对常见基于时间序列的DTW动作识别方法在准确性和实时性方面的不足,采用拆解手臂动作、构造子动作特征矩阵的方法,用子动作特征矩阵代替时间序列对手臂动作进行识别. 3) 选取6种生活中常见的手臂动作进行实验,与基于时间序列的DTW方法相比,本文方法在识别准确性和实时性上有显著提高,验证了本文方法的有效性. 4) 由于动作识别的准确性和实时性与特征选择紧密相关,因此后续研究将围绕手臂位姿变换,深入研究子动作特征的提取,以进一步提高识别的准确性并减少算法的延时性,为助残手智能控制打下基础.
3.2 子动作拆解

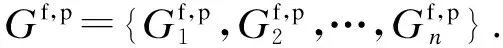
3.3 子动作特征矩阵构造

4 动作识别算法
4.1 DTW算法原理
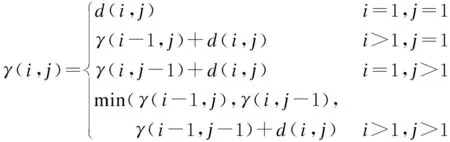
4.2 动作模板制作
5 实验
5.1 实验设计
5.2 实验结果分析

6 结论
