影响形状编码的表征元素感知差异量化研究

郭 琪 薛澄岐 于明玖

(1华东理工大学艺术设计与传媒学院， 上海200030)(2东南大学机械工程学院， 南京211189)(3西北工业大学机电学院， 西安710072)

目前，信息可视化界面正朝着高集成性、高动态化、强交互性的方向发展，这使得感知噪声的来源更复杂，可视化界面中信息编码感知的影响因素越来越多，可视化编码的难度也越来越大.形状编码作为人类视觉系统对可视化界面图形感知的基础，是用户最为擅长的用于判断和辨别的编码方式.例如，当判断不同线段的长度时，判断精度可以达到2%～3%[1].到目前为止，针对信息可视化形状编码的感知研究一般只讨论某个单一因素，如面积中的比例、角度或者轮廓长度等，并试图通过排除其他连续的空间维度(密度、距离、方向)等因素对形状编码感知的影响进行研究.例如Morgan[2]预测了椭圆纵横比的感知阈值，其研究结果表明形状的比较刺激与测试刺激的长宽比差异越大，面积大小的识别正确率便越差.随后Nachmias[3]证实并扩展了实验条件，通过比较实验分别测量了椭圆的长度和长宽比，并通过计算得到纵横比的感知量级最低.Tiurina等[4]研究了相同的尺寸在距离不同的情况下感知深度问题.Odic等[5]通过实验分析面积比率和数量比例的感知敏锐性问题，探讨面积感知与数量感知机制的潜在差异.Yousif等[6]研究了面积的扭曲对数量估计的影响.Ayzenberg等[7-8]通过眼动追踪实验范式，揭示人类视觉系统中形状骨骼的存在及其本质.随后Firestone等[9]和 Lowet等[10]通过实验研究图形形状的内部骨架如何影响形状的相似性感知.尽管这些研究提出了面积感知的影响因素，但仍有许多问题有待探究.首先，虽然已明确包括纵横比以及内部骨骼等影响面积感知敏锐性的因素，但是对人类视觉系统如何整合形状的多维尺度变量知之甚少；其次，现有的实验研究主要集中在面积或尺度大小的比较实验，在很大程度上忽略了被试在不同维度内的感知差异问题，例如在长度维度上具有更高的感知敏锐度是否可以预测维度更高的面积感知敏锐度.综上所述，目前尚缺乏对信息可视化界面形状编码感知差异量化的研究.

为实现对信息可视化界面形状编码的感知量化研究，需要对形状编码的感知过程进行建模.在建模过程中需要引入一个衡量标准，以便对感知变化进行量化.本文采用衡量刺激强度的变量——韦伯分数K对感知变化进行量化[11].Kay等[12]发现同一刺激差别量必须达到韦伯分数K才能被感知，韦伯分数K表明了刺激强度的百分比差异，即ΔI/I=K.其中，ΔI为在感知体验中能感受到的最小差异变量，也叫差异阈值，I为原始刺激量.

本文将在感知量化研究的基础上，提出影响形状感知的2类感知要素：长度和面积.通过实验分析长度和面积的视觉感知量化差异结果，并利用韦伯分数对形状编码的感知过程进行建模，最终构建形状感知的差异量化模型.

1 形状编码感知差异量化实验

1.1 实验被试

实验共计24名被试，所有被试均是机械学院的在读研究生，平均年龄22岁，男女比例1.1∶1(标准差μage=21.3，方差σa=10.3), 参与实验的被试视力或矫正视力均正常.实验开始之前，要求被试填写相关信息，包括姓名、年龄、专业、是否有过形状编码或可视化设计的实验经验等，并告知实验规则和流程.在实验中，如果被试的实验结果超过平均值2个标准差则要被剔除.基于此标准，每次试验中有1～2个被试的实验数据被剔除.

1.2 实验材料

所有被试都需要完成长度感知和面积感知量化实验.为了排除其他变量因素对视觉感知的影响，本文选取信息图表和可视化界面图标中相对比较简单的图形作为研究对象，比如正方形、圆形、三角形等，并将实验材料分为参考图形和调整图形2种.在长度感知任务的实验中，调整图形——弧线的中心角分别为60°、120°和180°三种；在面积感知任务的实验中，有不同图形(面积感知任务1)与相似图形(面积感知任务2)两种实验类型，其中相似图形实验类型中的调整图形——矩形的高宽比分别为2∶1、3∶1和4∶1三种，实验材料汇总如图1所示.

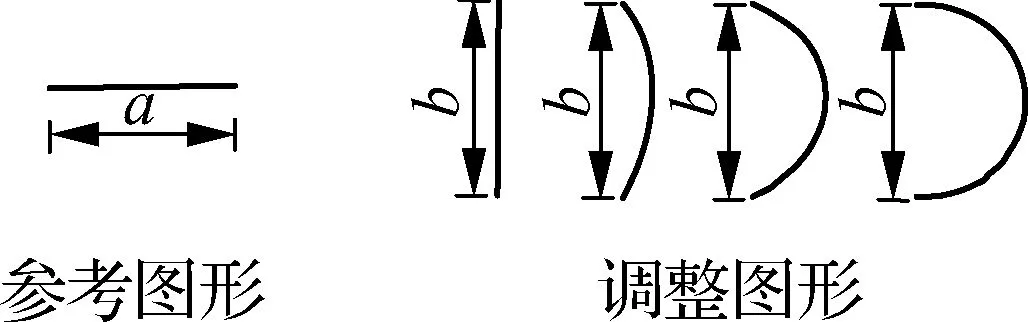
(a) 长度感知量化实验材料

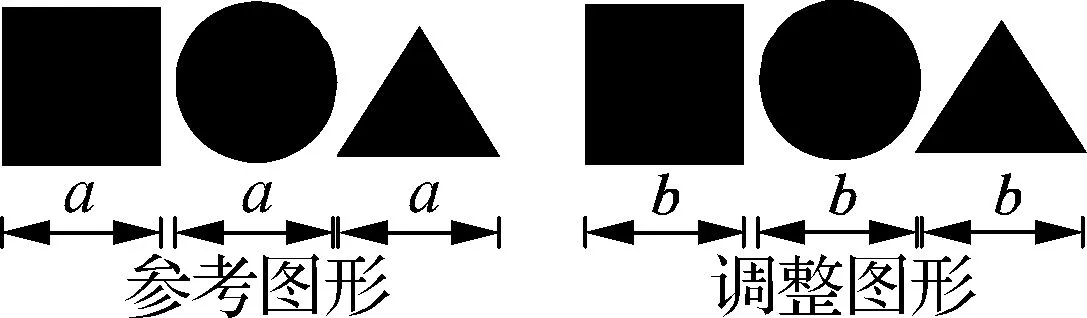
(b) 不同图形面积感知量化实验材料

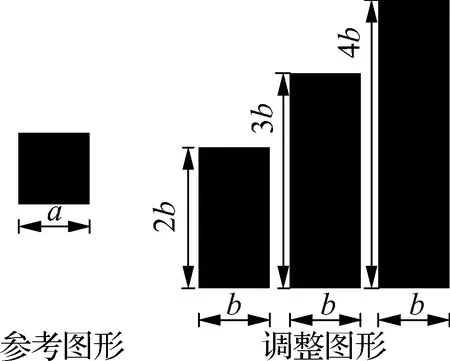
(c) 相似图形面积感知量化实验材料

其中边长为a的图形均为参考图形，边长为b的图形均为调整图形，并且a的边长设定为2、4和6 cm三个子条件，b的初始边长随机大于或小于参考图形边长，具体数据如表1所示.基于以上实验设置，长度感知实验一共有24个子条件，面积感知实验一共有54个子条件.为了防止被试在实验过程中存在视觉疲劳，每组任务完成后都有2 min的休息间隙.

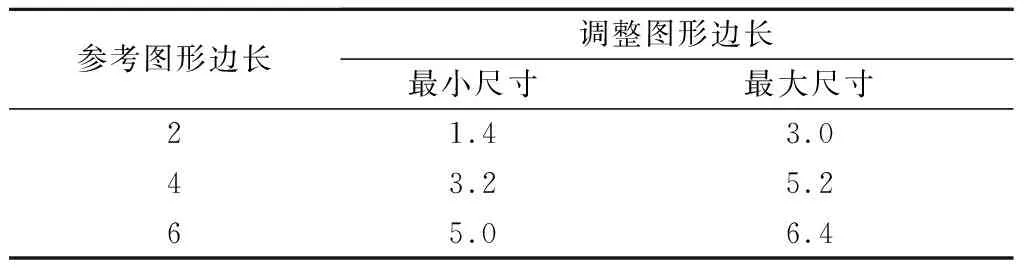
表1 图形边长初始值 cm

1.3 实验设备

在所有实验中，被试被要求坐在一台17英寸(43.18 cm)显示器前550 mm处，视角在2.0°～ 6.2°之间移动.用PR655光谱辐射计校准显示器上的色度和亮度，其中屏幕分辨率为1 280×1 024像素，亮度为92 cd/m2.每一组实验刺激由参考图形和调整图形组成，分别放置在显示屏两侧对称位置.

1.4 实验程序

被试对长度和面积的视觉感知变化量通过心理物理学的恒定刺激法测得，具体操作如下.

1) 对于长度感知量化实验，首先屏幕中心呈现实验指导语，按键盘任意键开始实验.随后屏幕中央呈现2个并排放置的线段，一个是恒定的参考线段，另一个是长度大于或小于参考线段的调整线段.通过键盘的Z键减小调整线段的长度，通过键盘的M键增加调整线段的长度，直到被试感知调整线段的长度和参考线段的长度相等为止，按空格键进入下一组长度感知条件.

2) 面积感知量化实验与长度感知量化实验的程序类似，一个是参考图形，另一个是面积高于或低于参考图形的调整图形，通过调整图形尺寸，直到被试感知到调整图形面积与参考图形面积相等为止.其中被试调整尺寸的时间与调整次数不受限制(单次调整尺寸值为0.015)，并且为了防止被试在实验过程中设置对齐参考线，随机设置调整图形在y轴方向与参考图形的垂直距离(±d/4，d为参考图形与调整图形的中心距离).

2 结果分析与讨论

在对实验结果进行分析前，为了削弱数据拟合模型的共线性和异方差性，对实验数据进行了对数转换，使实验数据更趋稳定，在最终剔除异常值后一共收集到了1 433个被试样本.随后采用互补误差函数erfc[13]确定被试在每组任务中的的韦伯分数：

(1)

式中，n1为长度差的均值；n2为面积差的均值.在该函数中，假定每组实验中调整图形与参考图形的长度差或面积差是沿着高斯随机变量的连续分布，则该函数只有一个自由度参数——韦伯分数K，用来表明高斯分布中的噪声量.较大的K值表示较高的噪声量，因此，韦伯分数越低表示任务绩效越好.对于每个被试的实验数据，选择最小平方误差，即预测数据和实际数据之间的平方差最小的K值作为最佳拟合值，通过剔除K值中与均值有2个标准差的偏差值，最终得到被试在面积感知实验任务和长度感知实验任务的韦伯分数如表2所示，表中展示了3种实验类型的韦伯分数对比，包括长度感知任务、面积感知任务1和面积感知任务2.

表2 每个子条件的面积和长度感知任务的韦伯分数值对比图

将长度与面积的韦伯分数通过Matlab软件中曲线拟合工具得到如下拟合方程：

KL=(log(KA+1))n-1 1.05≤n≤1.78

(2)

式中，KL表示长度的韦伯分数；KA表示面积的韦伯分数.为了防止拟合方程检验时误差为零，进行了多次多项式拟合.

2.1 组间效应量分析

被试在面积感知实验和长度感知实验中作出判断的平均时间分别为10.40和7.62 s.T检验结果显示不同性别和有无形状编码实验经验下，被试在绩效方面无显著性差异(不同性别显著性概率P1=0.113 8；有无形状编码实验经验显著性概率P2=0.093 8).组间ANOVA方差分析结果表明，在面积感知中，F检验的统计量F(2,30)=1.41,显著性概率P<0.001；在长度感知中，F(2,30)= 3.98,P<0.001，它们的尺寸平均值都存在显著性差异.而实验任务顺序不存在显著性差异，F(2,30)=2.47,P=0.34>0.05.

从表2可以看出，3种实验类型之间的平均韦伯分数K有显著性差异，F(2,35)=6.52,P<0.01.除此之外，测量模型和数据之间的拟合度R2在0.970～0.990之间，该值接近于1，表现出与韦伯定律一致的线性规律.

2.2 组内效应量分析

长度感知任务的感知阈值统计结果如图2所示.通过ANOVA方差分析发现，长度感知任务中不同子条件(实验编号1-1,1-2,1-3,1-4)之间不存在显著性差异，F(3,43)=0.018,P=0.997>0.05.这说明被试对长度的感知敏感性不受二维曲率影响，而且在不同子条件下，长度的感知尺度变化量与物理尺度变化量的对数值成正比.

面积感知任务1的感知阈值统计结果如图3所示.对单因素方差的分析结果显示，F(2,58)=16.11,P<0.001，说明不同形状之间的面积感知尺寸具有显著性差异，并且面积的视觉感知尺度变化量与物理尺度变化量的对数值成正比.

图2 长度感知阈值统计结果示意图

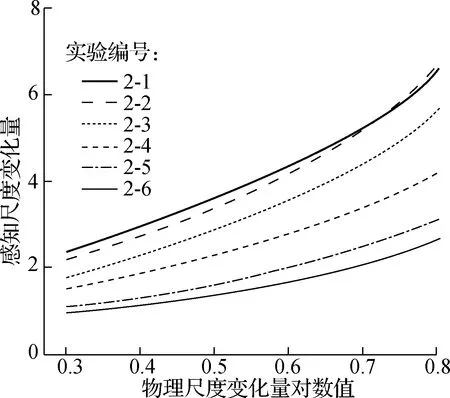
图3 面积感知的心理变化量统计示意图

基于上述对长度感知任务和面积感知任务的组内效应量分析可以得到，对长度或面积的心理感知尺度量的增加均少于长度或面积物理尺度量的增加，可用以下公式表示：

ΔR=log(I+ΔI)-logI

(3)

式中，ΔR表示长度或面积心理感知增量.

面积感知任务1和面积感知任务2的实验结果统计如图4所示.图中，误差条代表95%的置信区间，并非标准误差.多因素方差分析结果显示，F(2,42)=85.27,P=0<0.001，说明不同高宽比对面积感知的主效应显著，而且不同子条件(a=2，4，6 cm)和高宽比的交互效应显著，F(2,42)=8.37,P=0.001<0.05.

(a) 面积感知任务1

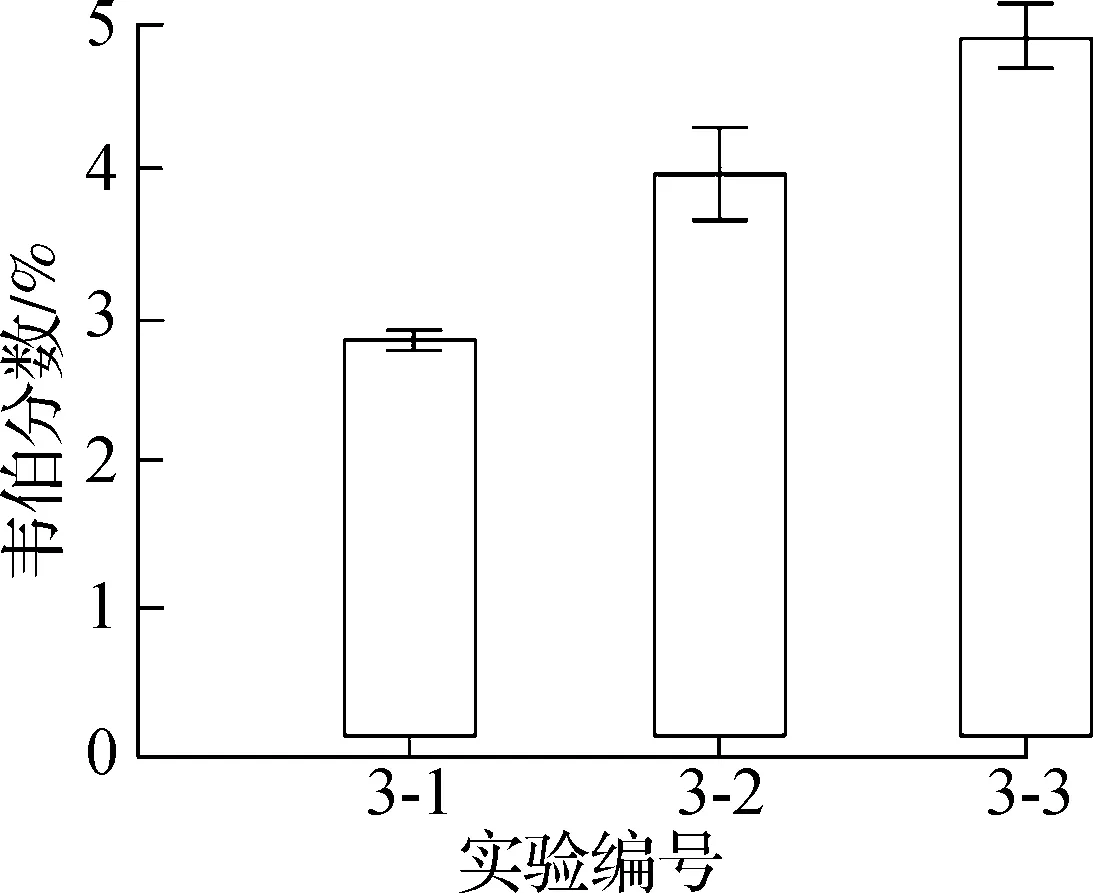
(b) 面积感知任务2

从图4(a)中不同形状的感知韦伯分数可以看出，参考图形为三角形、调整图形为圆形时的韦伯分数最高，在5%～ 6%之间，远高于参考图形为圆形、调整图形为三角形时的韦伯分数(在1%～2%之间).以上数据表明对面积的感知并不只依赖于对长度的感知，面积感知的过程是存在计算噪声的.其次，相较于三角形和圆形，对正方形的视觉感知敏感度最大，即感知敏感度从高到低依次为正方形、三角形、圆形.

2.3 讨论

2.3.1 长度感知实验

通过分析长度感知实验数据可以得到，即使在实验过程中设置不同中心角的弧度干扰，其长度感知的敏感度也不会受到二维曲率的影响，即单独的长度感知是不存在计算噪声的.

2.3.2 面积感知实验

对于不同图形的面积感知实验，若遵循卷积定律[14]，面积感知阈值应为单独长度感知阈值的均方根.但是，面积的实际感知阈值明显高于预测阈值，因此面积感知仅仅依赖于边长感知的独立模型是不可行的.除此之外，当观察者通过乘以他们对不同边长的估计值来感知不同形状的面积时，在做出乘法计算之后也会存在计算噪声，那么本文实验中正方形的计算噪声最大，即感知阈值最大，但是实验结果显示圆形的感知阈值最大.以上分析表明，观察者是使用多种启发式方法将宽度和长度感知阈值评估结合到面积感知阈值的评估中.如果调整图形的宽度和长度都大于参考图形，则被试易做出判断；如果调整图形的宽度较大，但长度较小，则可以通过确定与参考图形的宽度差异来进行判断.面积感知阈值的估算公式如下：

θ=λ1(α1-α2)∓λ2(β1-β2)

(4)

式中，θ表示面积感知阈值；λ1、λ2为决策变量权重，λ1+λ2=1；α1和β1分别为对应于参考图形的宽度和长度的随机变量，α2和β2分别为对应于调整图形的宽度和长度的随机变量，这意味着在长度差和宽度差的表示中存在计算噪声.

为了确认在长度差和宽度差的表示中是否存在计算噪声，通过在相似图形面积感知实验中设置不同长宽比进行验证.其实验结果显示，调整图形的长宽比越大，即长宽差异越大，面积的感知阈值越小.但是与不同形状的面积感知实验结果相比，被试已能够准确地感知相似形状的面积差异(K=2%～5%)，这意味着面积感知是可以通过长与宽来计算的.由于相似图形的长宽对比可以通过建立参考线进行感知，此时计算噪声较小，相比长宽尺寸在不同方向变化的情况会产生更高的感知精度.

3 应用实例探究

以上实验结果可以应用在信息点数量较多、信息点分布较为密集的实时监控信息界面中，如实时海图界面、实时调度界面和实时打击评估界面等.若需要视觉统计比较2组信息集合的大小，用长度表征信息时，需要长度差异阈值最低设定为0.02，可应用在柱状图或其变形图中；用面积表征信息时，圆形面积的差异阈值最低设定为0.06，可应用在饼状图或其变形图中.若需要视觉统计2组信息集合的变化趋势时，可以利用感知敏感度不同的正方形和圆形来表征不同信息，可应用在散点图或其变形图中.

4 结论

1)在对长度的感知过程中，即使存在不同中心角的弧线干扰，对长度的感知程度并没有显著性影响，即长度感知的敏感度不受二维曲率影响.

2)在对面积的感知过程中，不同形状和相似形状的面积感知均具有显著性差异，并且相较于三角形和圆形，观察者对正方形的视觉感知敏感度最大，即感知敏感度从高到低依次为正方形、三角形、圆形.

3)长度感知不存在计算噪声，面积感知存在计算噪声，并且长度和面积的感知尺度变化量与物理尺度变化量的对数值均成正比，即对长度或面积心理感知尺度量的增加均少于长度或面积物理尺度量的增加.

4)通过对影响形状编码的2种表征元素的感知建模，可知形状编码的韦伯分数可以通过面积和长度的韦伯分数共同计算得到.