新型冷弯薄壁型钢组合龙骨轴压性能试验研究
2021-08-06吕东鑫王泽辉朱洪磊
袁 泉 索 妮 吕东鑫 王泽辉 朱洪磊
(北京交通大学土木建筑工程学院, 北京 100044)
冷弯薄壁型钢结构体系通常由冷弯薄壁型钢构件和轻型板材组成,主要用于低层住宅、厂房建设中.传统冷弯薄壁型钢结构的基本构件为冷弯薄壁型钢龙骨,主要包含U形、C形等截面形式.
国内外许多学者对简单的U形和C形截面形式构件的承载力计算方法及屈曲机理开展了深入研究.文献[1-6]对C形截面构件的各类屈曲行为进行了理论分析和试验验证,得到了较为全面的冷弯薄壁型钢C形截面构件的破坏机理和破坏特征;文献[7-9]提出了冷弯薄壁型钢构件畸变屈曲承载力计算公式,建立了完善的有效强度法;文献[10-12]对冷弯薄壁型钢U形截面柱直接强度法的适用性进行了研究,对现有直接强度法公式进行了修正;文献[13-16]分析了冷弯薄壁型钢C形截面构件受压和受弯的屈曲后性能以及板组屈曲的相关作用;文献[17]针对加劲冷弯薄壁型钢槽形截面的非线性畸变屈曲运用能量法进行了推导分析,提出了适用于畸变屈曲构件的有效宽度法.然而,简单的U形、C形截面形式构件普遍存在承载能力低、易发生畸变屈曲等问题,使其在实际运用中均存在一定的局限性.
本文提出了一种冷弯薄壁型钢灌浆墙结构体系,对其基本构件——竖龙骨、立柱龙骨在竖向荷载作用下的屈曲模式及承载能力进行了试验研究,并利用ABAQUS有限元软件进行了精细化有限元模拟.结合试验及有限元结果,分析了国内现行冷弯薄壁型钢规范计算方法的局限性,并对其进行修正.
1 新型冷弯薄壁型钢组合龙骨及灌浆墙体
对传统的冷弯薄壁型钢结构墙体进行改良,优化了龙骨形式.竖龙骨和立柱均采用组合截面形式龙骨,通过自攻螺钉将连接件和分肢龙骨连接为整体(见图1).

(a) 竖龙骨
竖龙骨为双肢构件,分肢截面形式为帽形,连接件为矩形钢管;立柱为四肢构件,分肢截面形式为W形,连接件为方钢管.帽形与W形组合龙骨的承载能力强于普通的C形、U形构件,且便于设置连接件,形成格构式构件,连接件的间距可根据外侧板材的尺寸自由调整.此外,在竖龙骨中间插入Z形斜撑,通过自攻螺钉与竖龙骨及立柱连接.墙体内还设置2道横撑,连接立柱、竖龙骨及斜撑龙骨,约束龙骨变形,提高结构整体性.竖龙骨、立柱、斜撑、横撑以及上下U形导梁共同组成钢骨架(见图2).
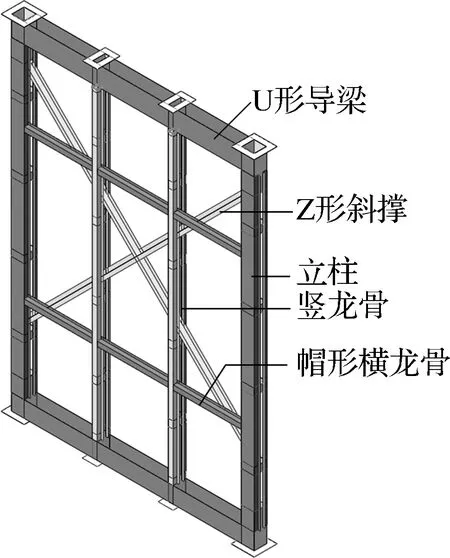
图2 墙体钢骨架构造
在钢骨架一侧安装陶土板,另一侧安装硅酸钙板,形成空腔.空腔内浇筑聚苯颗粒混凝土,与钢骨架共同组成新型冷弯薄壁型钢灌浆墙体.
2 试验
2.1 试件制作
根据实际灌浆墙结构的龙骨尺寸,设计制作了3个竖龙骨试件(编号为SLG1~SLG3)和3个立柱试件(编号为LZ1~LZ3),进行平行试验.试件长度均为3 040 mm.试件的详细构造及横截面形式见图3.

(a) 竖龙骨
2.2 加载设备与加载制度
采用单调加载方式对试件施加轴向荷载.试件下端采用单向刀铰支座,以控制构件的转动方向;上端由30 t量程的液压千斤顶加载,千斤顶自带半球形铰支座.本次加载由应变式传感器进行荷载控制.试验装置见图4.

图4 竖向加载装置
2.3 测点布置
每个试件上布置10个应变片,编号为S1~S10,反对称布置于试件各截面上(见图5).每个试件上布置3个位移计,编号为D1~D3.其中,D2和D3按对角线布置于试件顶部,可同时测量试件的竖向变形和转角.
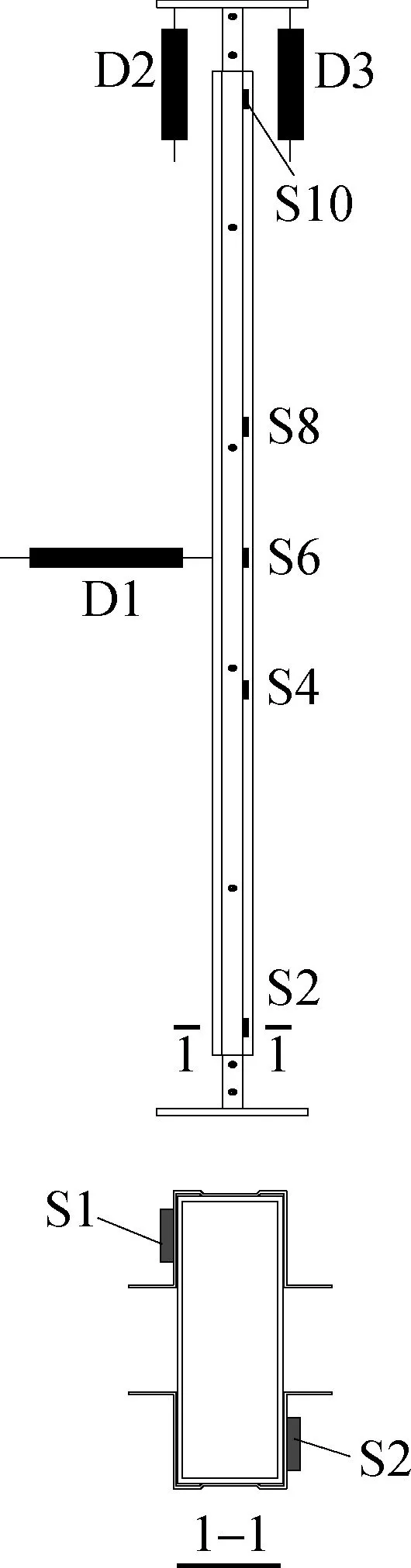
(a) 竖龙骨
3 试验结果及分析
3.1 试件破坏特征
试验照片见图6.由图6(a)~(f)可以看出,试件SLG1~SLG3的破坏现象类似,均发生畸变屈曲,且分别在不同连接件处发生弯折.稍有不同的是,试件SLG2底端出现局部屈曲,而试件SLG3存在轻微的扭转现象.
试件LZ1~LZ3在加载过程中均始终保持挺直.由图6(g)~(l)可以看出,加载后期北侧W形龙骨出现了不同程度的内凹、外凸现象,从而引起整个试件的弯折破坏.

(a) SLG1整体弯折

(d) SLG2局部屈曲

(g) LZ1分肢内凹

(j) LZ2畸变屈曲
3.2 荷载-应变曲线
图7(a)和(b)为试件SLG2的荷载-应变曲线.由图可知,试件南北两侧的应变均呈现一侧大、另一侧小的规律,表明试件发生了弯曲破坏.同一侧各应变变化规律基本一致,均随着荷载的增大而增大,说明试件受力比较均匀.顶部和底部应变略大,表明竖龙骨的端部承受更大的荷载.试件SLG1和SLG3的荷载-应变变化规律与试件SLG2类似.
试件LZ2的荷载-应变曲线见图7(c)和(d).
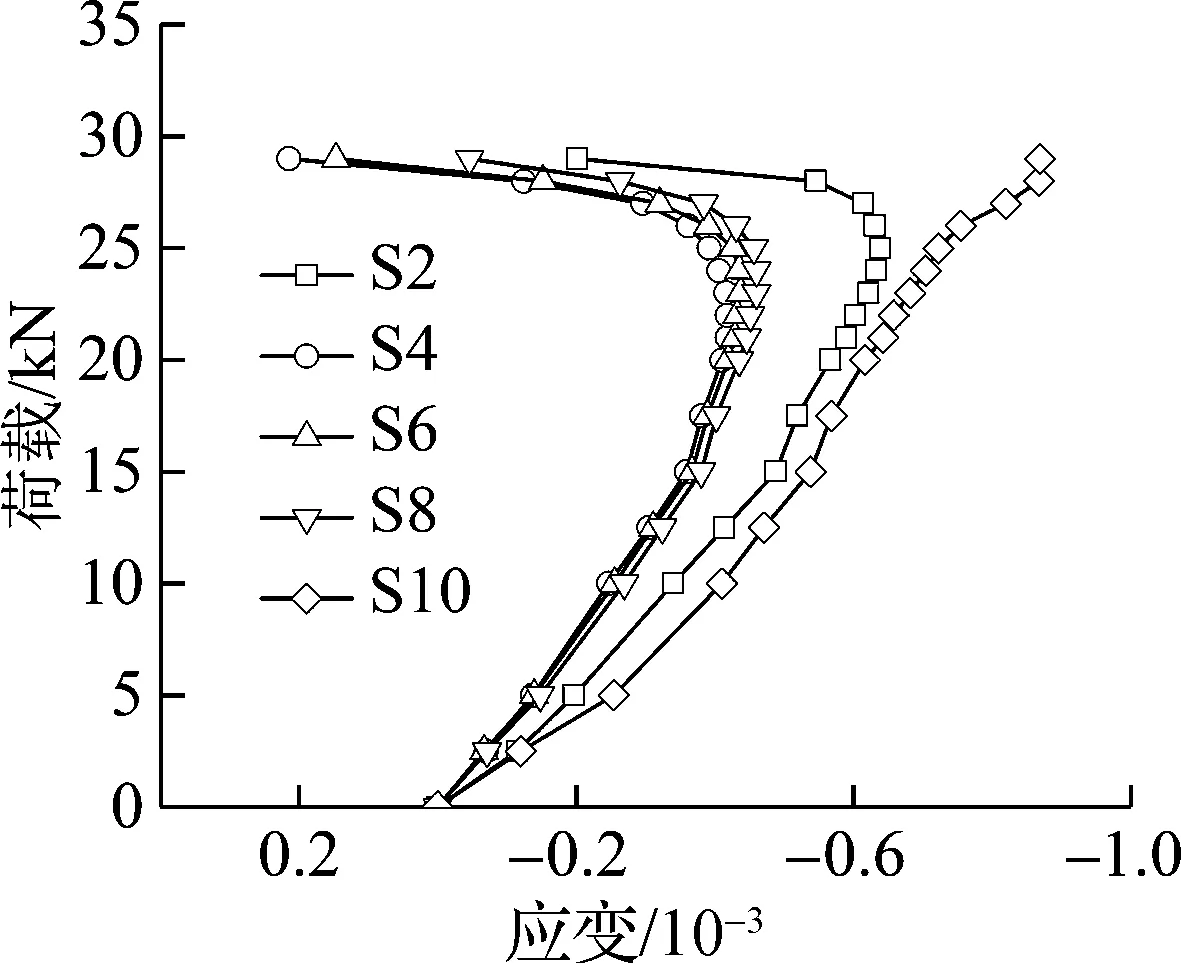
(a) 试件SLG2南侧
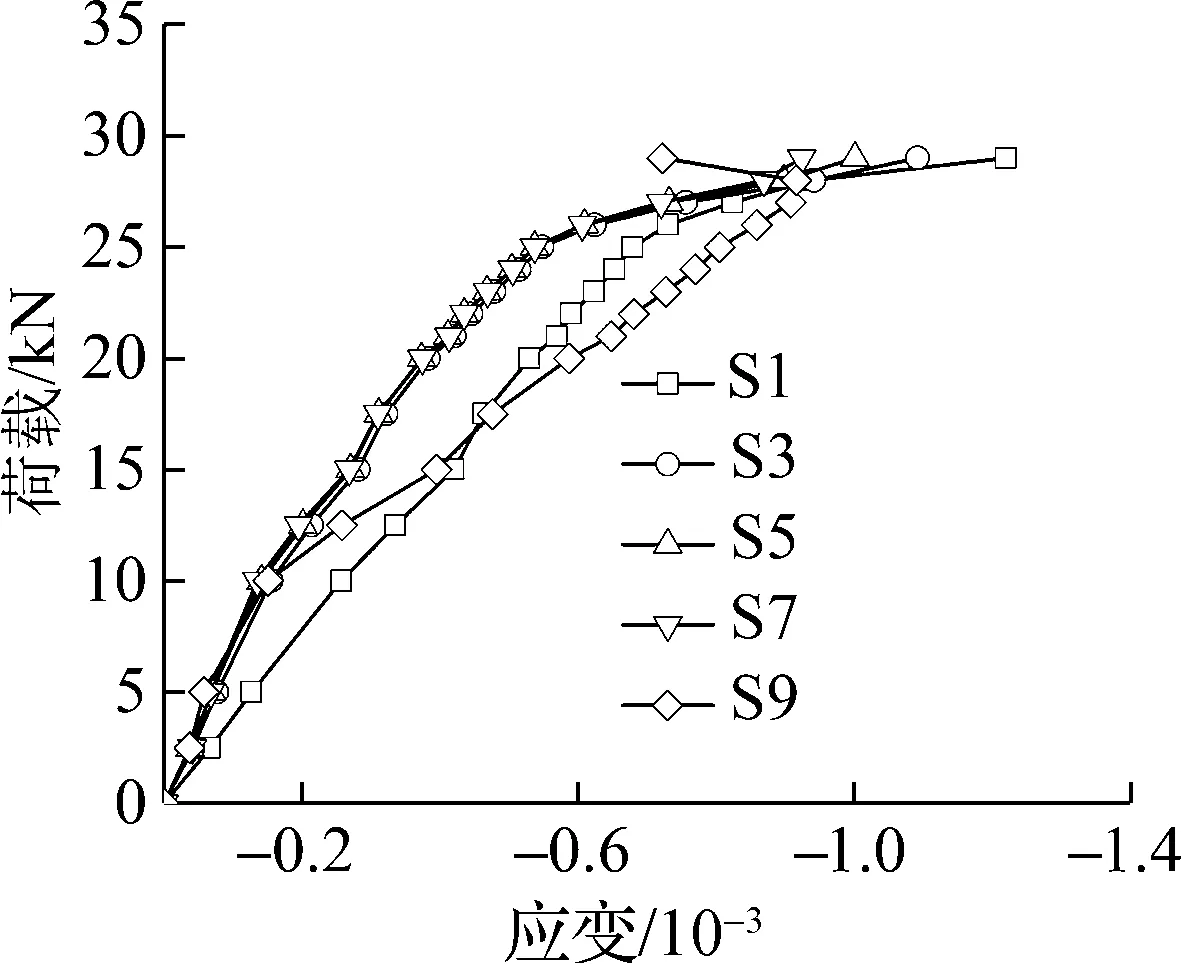
(b) 试件SLG2北侧

(c) 试件LZ2南侧

(d) 试件LZ2北侧
由图可知,最后一级加载前,应变均随着荷载的增大而增大,截面南北两侧的应变值差异不大,表明立柱轴向受力均匀,弯曲现象不明显.达到荷载极限时,试件多部位已进入塑性状态,且塑性阶段较短. 与竖龙骨类似,立柱的端部受力略大于其他部位.试件LZ1和LZ3的荷载-应变变化规律与试件LZ2类似.
3.3 极限承载力与破坏模式
各试件的极限承载力Put和破坏模式见表1.由表可知,试件SLG1~SLG3的极限承载力均值约为28.33 kN,试件LZ1~LZ3的极限承载力均值约为127 kN.试件SLG1和SLG3发生了整体弯曲屈曲破坏,试件SLG2因某肢帽形龙骨的畸变屈曲而发生整体弯扭屈曲破坏.试件破坏均伴随有畸变屈曲,破坏位置存在一定的离散性(见表1).加载过程中,立柱先在中部或中下部位发生畸变屈曲,进而发生整体弯折破坏.
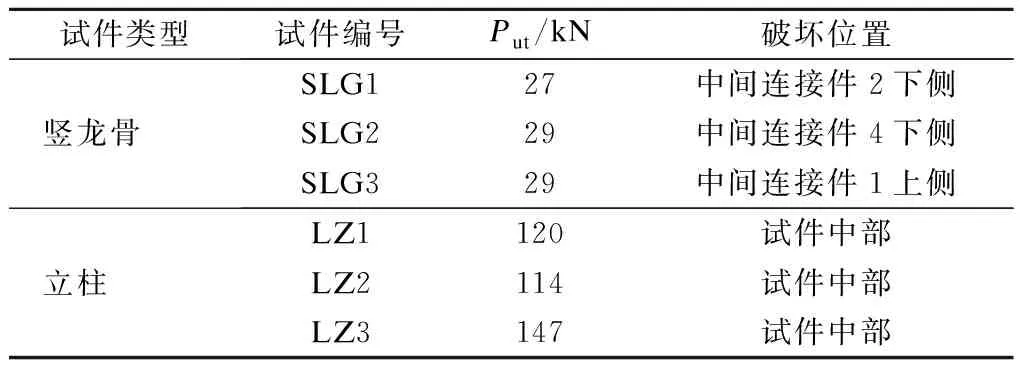
表1 各试件的极限承载力与破坏模式统计
各试件的荷载-位移曲线见图8.由图可知,顶部竖向位移约为4 mm时,立柱和竖龙骨的荷载分别约为108和25 kN,立柱的轴压承载力约为竖龙骨的4.5倍,刚度约为竖龙骨的4.3倍.立柱为轻钢灌浆墙结构的主要承压构件,竖龙骨柔度大、承载力低,不适宜单独作为竖向受力构件.通过与C形及U形构件轴压试验数据[10-15]对比发现,采用帽形和W形截面的龙骨具有更高的极限承载力.
4 承载力分析与比较
4.1 分析方法
采用2种不同的分析方法对轴压下的竖龙骨、立柱试件极限承载力进行计算.
首先,采用ABAQUS有限元软件计算试件极限承载力.试件采用S4R壳单元,上下垫板采用C3D8R实体单元.考虑材料的几何非线性,对所有构件均采用理想弹塑性本构模型进行模拟.由于制作误差、材料缺陷等因素的影响,试件存在初偏心,因此有限元模拟时先对竖龙骨和立柱进行特征值分析.根据屈曲模态分析结果和试件破坏现象选取相应的模态,施加的整体初始缺陷幅值为l/750,其中l为试件长度;施加的局部初始缺陷幅值等于翼缘宽度.特征值分析完成后,对试件进行正式的屈曲分析,分析时考虑试件的结构非线性,采用弧长法进行计算.试验时,试件上部为半球铰支座,下部为单刀口铰支座.根据支座特点,对试件的边界条件进行定义.竖龙骨及立柱有限元模拟结果见图9.
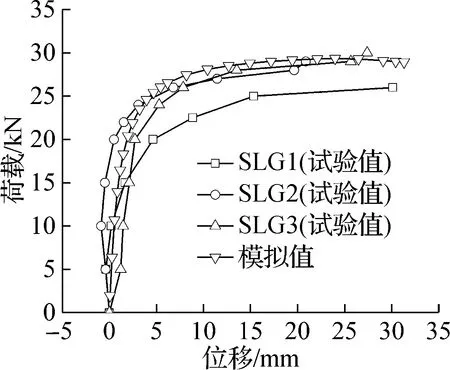
(a) 竖龙骨荷载-中部横向位移
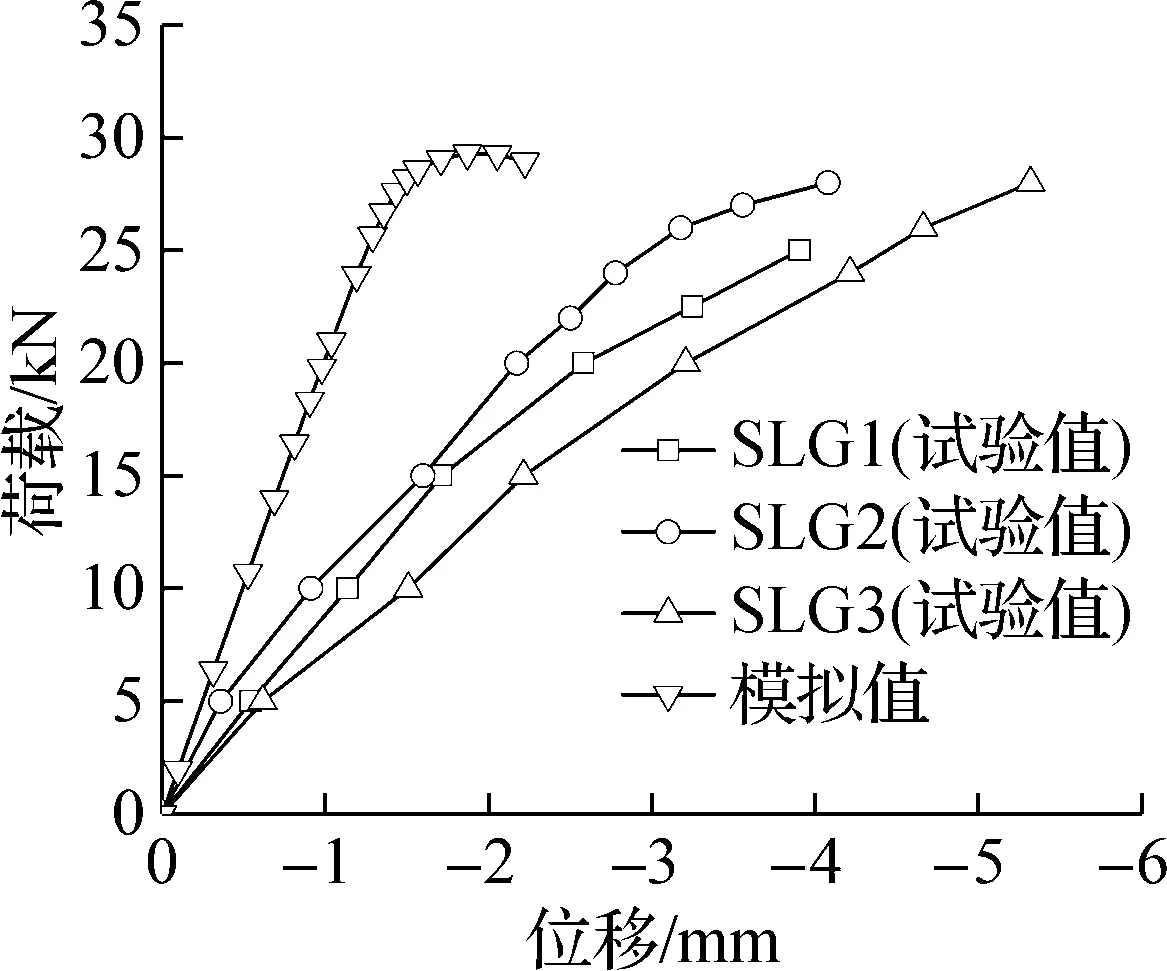
(b) 竖龙骨荷载-顶部竖向位移

(c) 立柱荷载-中部横向位移

(d) 立柱荷载-顶部竖向位移
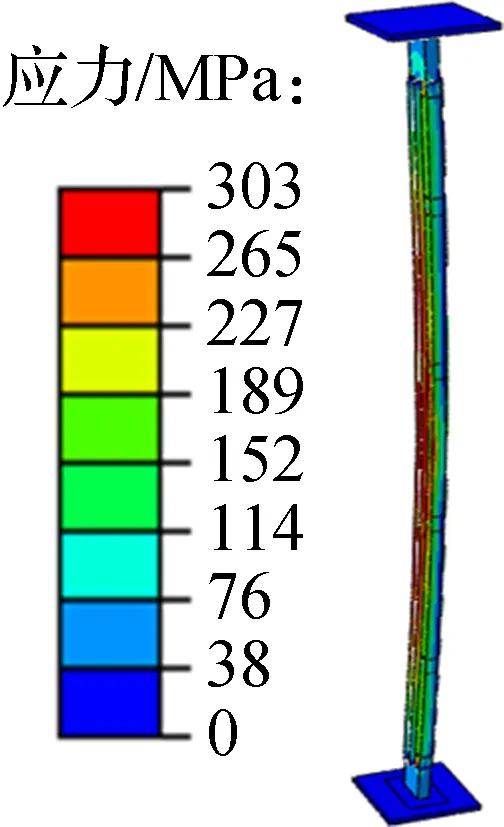
(a) 竖龙骨
然后,参考《冷弯薄壁型钢结构技术规范》(GB 50018—2002)[18]中的相关计算方法,确定竖龙骨和立柱的有效截面面积,计算竖龙骨及立柱的轴压承载力.将竖龙骨和立柱看作格构柱,计算得到其最大长细比分别为141.11和71.58,稳定系数分别为0.274和0.733.竖龙骨的有效截面面积与毛截面面积相等,均为292.00 mm2;立柱的有效截面面积为452.00 mm2,小于其毛截面面积736.44 mm2.结合前期材性试验结果,最终计算得到竖龙骨和立柱承载力分别为24.25和92.70 kN.
4.2 结果比较
荷载-位移曲线的模拟结果与试验结果对比见图8.由图8(a)和(c)可以看出,试件中部横向位移的试验值与模拟值吻合较好,模拟值介于3组试件试验值之间.对比图8(b)和(d)可以看出, 在相同荷载下,顶部竖向位移模拟值小于试验值,说明竖向刚度模拟值较试验值偏大.究其原因为有限元模拟时,在自攻螺钉连接部位采用绑定约束模拟,忽略了自攻螺钉实际的转动和滑移以及构件接触面的脱离,导致试件刚度偏大.
分别采用有限元模型和规范[18]中的计算方法求得各试件的极限承载力Puf和Pu,并与试验结果极限承载力Put进行对比,结果见表2.由表可知,各试件的极限承载力模拟值与试验值较为接近,最大误差不超过12%,从而验证了有限元模型的正确性.模拟值稍高于试验值,这是因为建模时对自攻螺钉连接强度模拟不够精确,忽视了螺钉的剪切和滑移现象,且对试件施加的初始缺陷难以与实际情况完全一致.根据规范[18]中计算方法得到的极限承载力计算值较试验值和模拟值偏低,尤其是对于立柱,其极限承载力计算值与试验值、模拟值相差均超过25%,计算结果较为保守,因此需要对规范[18]提出的计算方法进行修正.

表2 极限承载力计算值与试验值的比较
4.3 计算方法修正
采用规范[18]中计算方法结果偏低的原因可能是由于实际的竖龙骨和立柱分肢龙骨并非通长设置,其上下端部的连接件仅连接部分分肢龙骨.端部连接件惯性矩和刚度与分肢龙骨相比较大,计算过程中将构件简化为格构式柱弱化了端部的约束效果.因此,本文对试件的长细比λ进行修正.分肢龙骨的实际长度与构件总长度比值为
修正后的长细比为
λ′=ηλ=0.89λ
按照规范[18]中的板件定义方式和有效宽厚比计算方法得到的立柱有效截面面积远小于毛截面面积.究其原因在于,进行立柱有效截面面积计算时,将20 mm宽的板件B1、B4全部划分为卷边(见图10(a)).实际计算发现,其高厚比远大于规范[18]中卷边的最小高厚比限制6.4和6.2,导致整体截面面积计算结果较为保守.为保证最小卷边宽度,将同一板件划分为2种类型,对立柱的有效截面面积进行修正.重新划分板件B1和B4,增加板件B5和B6(见图10(b)),其宽度按照规范[18]要求的最小卷边长度确定, 计算时将板件B1和B4看作部分加劲板件.修正后竖龙骨和立柱的计算结果见表3.表中,Pus为修正后的试件极限承载力规范计算值.
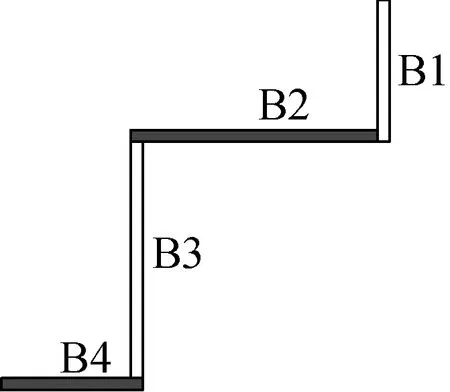
(a) 修正前

表3 修正后竖龙骨和立柱的计算结果比较
由表3可知,采用修正计算方法得到的试件轴压承载力计算值与试验值、模拟值接近.竖龙骨的计算值略高于试验值和模拟值,最大误差不超过6%.立柱计算值和试验值基本吻合,相较于有限元模拟值低13%,因此采用该方法计算竖龙骨和立柱的轴压承载力是安全可靠的.
墙体外挂板通过一种可调式定位部件连接到结构主体,在结构主体受力时外挂板可随可调式定位部件运动,故外挂板几乎不承担竖向荷载.轻钢灌浆墙体的主要竖向承载力由钢龙骨、聚苯颗粒泡沫混凝土承担.
5 结论
1)竖龙骨的破坏模式为整体屈曲破坏,具体表现为弯曲屈曲,同时伴随有畸变屈曲.立柱的破坏模式为先发生畸变屈曲,随后试件整体屈曲破坏.立柱受压承载力较高,在结构体系中作为主要的承力构件;而竖龙骨由于柔度大,承载力较低,不适合单独作为受压构件.
2)利用有限元软件ABAQUS对竖龙骨、立柱分别进行了数值模拟.模拟得到的极限荷载及破坏模式与试验结果吻合较好,说明ABAQUS软件可以较为准确地模拟冷弯薄壁型钢多肢组合截面龙骨的受压破坏模式和极限承载力.
3)采用我国现行规范中的计算方法对竖龙骨和立柱2种多肢组合截面龙骨的轴压承载力进行计算,计算结果与试验值相比过于保守.鉴于组合截面龙骨构造的特殊性,本文对试件长细比与有效截面面积的计算方法进行了修正.修正后的计算结果与试验结果及有限元模拟结果吻合较好,计算结果偏于安全.
