混凝土浇筑期考虑节点搭接缺陷的模板支架概率极限状态设计
2021-08-06刘芷廷秦非非
杜 涛 谢 楠 刘芷廷 秦非非
(1北京交通大学土木建筑工程学院, 北京 100044)(2 通州区发展和改革委员会, 北京 101100)
模板支架是一种重要的临时结构,在施工过程中用以承受新浇混凝土、钢筋、堆放材料、施工设备及施工人员的质量等.近年来,模板支架频繁发生坍塌事故,其中74%的模板支架是在浇筑混凝土时倒塌的[1].Buitrago等[2]提出在建建筑物倒塌事故最常见的原因之一是混凝土浇筑过程中模板支架的倒塌.在混凝土浇筑期,施工荷载不仅包括施工人员及设备的自重(施工活荷载),还包括逐渐增加的塑性混凝土荷载.施工荷载所产生的高可变荷载效应与一般的低可变荷载效应有所区别.我国现行相关规范《建筑施工模板安全技术规范》(JGJ 162—2008)[3]和《建筑施工扣件式钢管脚手架安全技术规范》(JGJ 130—2011)[4]将混凝土荷载作为永久荷载考虑.因此,有必要针对混凝土浇筑期高可变荷载效应的特点进行深入研究.
人为错误是影响模板支架安全性的重要因素.模板支架的倒塌风险可能源于结构抗力、荷载的不确定性和人为错误[5].目前,关于模板支架中人为错误的研究主要集中于对人为错误的调查统计[6-7]及其对模板支架抗力的影响方面[8-9],关于荷载效应的影响性研究则较为少见.Ikäheimonen[10]和Zhang等[11]对立杆荷载效应进行调研时发现,模板支架上部存在节点搭接缝隙(即节点搭接缺陷).
概率极限状态设计法是解决模板支架安全问题的首要途径.以往由于模板支架失效而发生的各种严重事故都表明,建立可靠的设计方法十分必要[9].目前,针对模板支架概率极限状态设计方法的研究还比较少,文献[12-13]分别对扣件式和碗扣式模板支架规范所采用的概率极限状态设计表达式中的分项系数进行了分析和调整,但是均没有考虑混凝土浇筑期存在高可变荷载效应的情况以及节点搭接缺陷的影响.
本文以模板支架为研究对象,提出考虑节点搭接缺陷的概率极限状态设计方法.通过施工现场调研获得节点搭接缺陷的发生规律,对节点搭接缺陷进行仿真模拟,探究施工荷载以及模板支架跨数对荷载效应系数的影响.基于可靠度理论,分别建立考虑和不考虑节点搭接缺陷2种情况下的概率极限状态设计表达式,并将所得结果与《建筑施工扣件式钢管脚手架安全技术规范》(JGJ 130—2011)中的可靠度指标进行比较.
1 节点搭接缺陷调研及统计特性
1.1 调研方法
在混凝土浇筑期间,对天津长江道尚斓苑项目、中关村高端医疗器械产业园、北京交通大学校内项目和天津半湾花园项目4个工地进行初步调研,发现模板支架上部结构均存在较多处的节点搭接缺陷.
在对节点搭接缺陷进行现场测量的过程中,主要关注主龙骨与U形托之间的缝隙宽度及主龙骨与次龙骨之间的缝隙宽度,缝隙宽度由钢卷尺或者扑克牌测量.对于缝隙较大的情况,直接用钢卷尺测量,为了减小读数误差,对同一缝隙进行多次测量,对结果取平均值,测量方法见图1(a);对于缝隙较小的情况,采用记录塞入扑克牌张数的方法测出缝隙宽度,单张扑克牌的厚度利用游标卡尺测量,测量方法见图1(b).

(a) 钢卷尺测量缝隙
1.2 节点搭接缺陷的统计特性
在混凝土浇筑前,调查研究了节点搭接的含缝情况.对于455个主龙骨与U形托搭接位置点,发现存在含缝位置点100个,含缝率为21.98%;对于1 037个主龙骨与次龙骨搭接位置点,发现存在含缝位置点384个,含缝率为37.03%,部分次龙骨未参与工作.表1列出了主龙骨与U形托、主龙骨与次龙骨之间缝隙参数的统计特性.

表1 缝隙参数统计特性
2 浇筑期考虑节点缺陷的仿真方法
2.1 节点搭接缺陷的模拟方法
在实测存在节点搭接缺陷的搭接点处,选用带缝的COMBIN40弹簧单元进行模拟.为保证结构体系的稳定性,搭接点处无节点搭接缺陷的立杆采用杆单元模拟.存在节点搭接缺陷的模型见图2.在主龙骨与U形托之间以及主龙骨与次龙骨之间存在节点搭接缺陷的情况下,含缝立杆和含缝虚拟立杆均采用COMBIN40弹簧单元进行模拟.

图2 考虑节点搭接缺陷的有限元模型
每个搭接位置点只有存在与不存在节点搭接缺陷2种可能,即每个搭接点处有缝与无缝是2个对立事件,符合伯努利分布的基本条件,采用含缝率确定伯努利分布中输出为1的概率.当伯努利判断结果为1时,根据相应参数的指数分布输出随机缝隙宽度值;当伯努利判断结果为0时,表示搭接点处无节点搭接缺陷,缝隙宽度值输出为0.
2.2 荷载施加方法
所调研的4个工地均为常见的S形浇筑模式[14],故本文采用此浇筑模式对模板支架施加荷载.为实现混凝土浇筑过程模拟,将模板细化.在一个相邻立杆围成的区域内,将模板分成均等的若干单元.施加荷载时,将荷载依次施加在每块划分单元上.以跨数为5×5(纵向×横向)且立杆间距为1.2 m的模型为例,混凝土浇筑过程模拟路线见图3.模板单元1~25依次逐级施加施工荷载.

图3 混凝土浇筑过程模拟路线图
2.3 计算精度验证
天津半湾花园项目的实测范围包含整个混凝土浇筑过程,获得了较为完备的测量数据,故参照此项目的测量数据对所建模型进行精度检验.取1块典型模板,现浇楼板厚度为0.2 m;模板支架搭设高度为3.05 m;立杆的纵横向间距和步距均为1.2 m;主龙骨尺寸为87 mm×87 mm,间距为1.2 m;次龙骨尺寸为38 mm×87 mm,间距为0.2 m.
混凝土浇筑前,立杆顶端的主龙骨与U形托之间有3个存在节点搭接缺陷的位置点,占同种搭接位置点总数的18.75%.经测量,这3个搭接位置点处的缝隙宽度分别为1.5、0.9和2.3 mm.模拟计算结果显示,加载后这3个搭接位置点的缝隙全部闭合,即缝隙宽度均为0,与实测浇筑混凝土后的结果一致.
主龙骨与次龙骨之间有28个存在节点搭接缺陷的位置点,占同种搭接位置点总数的36.84%,将这28个存在节点搭接缺陷的缝隙进行编号,编号依次为1~28.将加载后主龙骨与次龙骨搭接位置点的实测缝宽与有限元模拟计算缝宽进行比较,结果见图4.由图可知,模拟结果与实测结果的相对误差大多低于10%,仅存在个别相对误差较大点,属于工程上可接受误差范围.
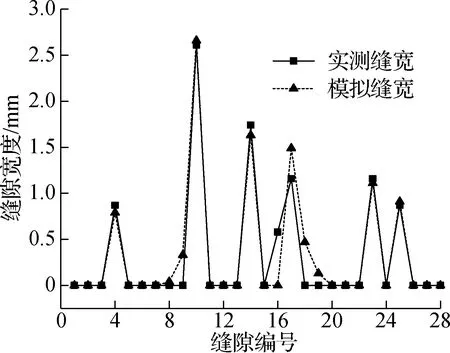
图4 实测缝宽与模拟缝宽对比
由此可知,本文建立的非线性有限元模型在模拟节点搭接缺陷方面具有较高的精度.
3 节点搭接缺陷对荷载效应系数的影响
3.1 荷载效应系数
本文主要研究混凝土浇筑过程中由施工荷载Fcon产生的荷载效应最大值所对应的荷载效应系数C.采用承载面积法计算单根立杆上所承受的荷载,由荷载与荷载效应之间的关系可知,单一工况下立杆所对应的荷载效应系数为
(1)
式中,Smax为混凝土浇筑过程中立杆所产生的荷载效应最大值;An为立杆负荷的模板面积;Q1为混凝土荷载;Q2为施工活荷载.
3.2 考虑节点搭接缺陷荷载效应系数的统计特性
根据以往施工经验,将施工荷载以及支架跨数作为影响荷载效应系数C的主要因素.通过控制单一变量的方法,对不同跨数、不同施工荷载工况下的模板支架进行仿真计算.除跨数不同外,模板支架其他搭设参数均与2.3节中天津半湾花园项目典型模板的搭设参数一致.为保证计算结果的精度、节省计算时间,将单工况下模板支架的模拟次数取为800.对荷载效应系数C的仿真结果统计整理,得到其统计参数.经假设检验,C服从正态分布.模板支架计算工况及荷载效应系数统计参数见表2.由表可知,节点搭接缺陷的存在使模板支架的荷载效应系数C由常量变为随机变量.C的均值在1.0左右变化,说明其受施工荷载及支架跨数的影响较小.C的变异系数δC随支架跨数的增加而增加,这是因为伴随着系统规模(支架跨数)的增大,模板支架中存在的含缝率也增加,从而导致荷载效应系数的变异性增大,立杆上荷载效应的分布更加不均匀.此外,施工荷载对荷载效应系数变异性的影响远大于支架跨数的影响.

表2 模板支架计算工况及荷载效应系数
4 节点搭接缺陷对设计方法的影响
4.1 概率极限状态设计方法
在混凝土浇筑期间,混凝土在凝固前本身具有可塑性的特点,混凝土浇筑的过程也是混凝土荷载从无到有的过程,因此考虑将混凝土荷载作为可变荷载或施工荷载,而非设计规范[3-4]中将其视为永久荷载.
结构可靠性的功能函数为
Z=R-S
(2)
式中,R为极限承载力;S为荷载作用效应.
将混凝土荷载作为施工荷载,则采用的概率极限状态表达式为
(3)
式中,Rk为抗力标准值;SGk为永久荷载效应标准值;SQ1k为混凝土荷载效应标准值;SQ2k为施工活荷载效应标准值;γ0=0.9为结构重要性系数;γR、γG、γQ1、γQ2分别为抗力、永久荷载、混凝土荷载和施工活荷载的分项系数.为简化计算,假设γQ1=γQ2,则式(3)转化为
(4)
式中,γQ为施工荷载的分项系数.
4.2 荷载统计模型
在混凝土浇筑期,模板及面上的永久荷载主要包括钢筋和模板自重.钢筋和模板自重均值μG与标准值Gk之比取为1.05,变异系数δG取为0.15.
在混凝土浇筑期,施工荷载主要包括混凝土荷载Q1和施工活荷载Q2.本文采用文献[15]的统计结果,施工荷载的统计参数选取如下:混凝土荷载的均值μQ1与标准值Q1k之比为1.19,变异系数δQ1为0.09,服从正态分布;施工活荷载的均值μQ2与标准值Q2k之比为0.33,变异系数δQ2为0.13,服从对数正态分布,且将施工活荷载标准值Q2k取为2.5 kPa.
4.3 立杆荷载效应
考虑到常用现浇钢筋混凝土板厚大于120 mm,故施工荷载设计值一般大于5 kPa.当施工荷载大于9 kPa时,荷载效应系数变化极小,故将表2中的施工荷载7、9、11、13 kPa所对应的荷载效应系数均值及变异系数分别取平均值,得到考虑节点搭接缺陷时的荷载效应系数均值μC=1.01,变异系数δC=0.24.另外,由于钢筋和模板自重所产生的立杆荷载效应相对于混凝土荷载和施工活荷载所产生的立杆荷载效应小,故在不考虑节点搭接缺陷的影响时,荷载效应系数取为常量1.0.
综上所述,考虑节点搭接缺陷时,立杆上荷载效应SE的表达式为
SE=[G+C(Q1+Q2)]An
(5)
式中,G为模板及面上的永久荷载.
不考虑节点搭接缺陷时,永久荷载和施工荷载所对应的荷载效应系数均为常量1.0,立杆上荷载效应的表达式为
S=(G+Q1+Q2)An
(6)
4.4 抗力统计模型
文献[13]采用Monte Carlo模拟方法,计算得到15种扣件式模板支架抗力的统计参数.本文选取其中一种具有代表性的模板支架的抗力统计参数进行研究,即均值μR与标准值Rk之比为1.07,变异系数δR为0.26,标准值Rk为36.27 kN,服从对数正态分布.
4.5 分项系数计算分析
鉴于我国现行规范[3-4]并未明确给出抗力分项系数的取值,故采用美国ASCE规范[16]给出的抗力分项系数与其统计参数的关系表达式,即
(7)
式中,αR为敏感系数,此处近似取为0.7;βT为结构体系的目标可靠度指标,此处取为3.2[13].
根据式(7)和本文所采用的抗力统计参数,计算得到考虑与不考虑节点搭接缺陷时的抗力分项系数γRE和γR均为1.7.
若要获得一组最佳的荷载分项系数,则应使相对累积误差值I最小[17],其表达式为
(8)
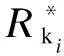
在混凝土浇筑期,主要考虑以下2种情况:① 存在节点搭接缺陷,永久荷载分项系数γGE的可能取值为1.1、1.2、1.3,施工荷载分项系数γQE的取值范围为1.7~2.1;② 无节点搭接缺陷,永久荷载分项系数γG的可能取值为1.1、1.2、1.3,施工荷载分项系数γQ的取值范围为1.4~1.7.这2种情况下的相对累积误差值I与荷载分项系数的关系曲线见图5.由图可知,考虑节点搭接缺陷时,最佳荷载的分项系数取值为γGE=1.2,γQE=1.9;不考虑节点搭接缺陷时,最佳荷载的分项系数取值为γG=1.1,γQ=1.55.为与我国现行规范[3]保持一致,将永久荷载的分项系数取为1.2,从而保证荷载效应的设计值不会产生大幅度变化.

(a) 考虑节点搭接缺陷

(b)不考虑节点搭接缺陷
考虑节点搭接缺陷时,概率极限状态设计表达式为
(9)
不考虑节点搭接缺陷时,概率极限状态设计表达式为
(10)
我国现行规范[4]规定,不组合风荷载时模板支架立杆稳定性的极限状态设计公式为
0.9(1.2SGk+1.4SQk)≤φAf
(11)
式中,SQk为可变荷载效应标准值;φ为轴心受压构件的稳定系数,根据长细比λ确定;A为立杆截面面积;f为钢材的抗压强度设计值.
按照本文方法和规范[4]分别设计模板支架,比较其可靠度指标β,结果见图6.共分为以下4种情况:① 按照本文方法进行设计且考虑节点搭接缺陷;② 按照本文方法进行设计且不考虑节点搭接缺陷;③ 根据规范[4](即式(4)和(11))进行设计且不考虑节点搭接缺陷;④ 根据规范[4](即式(4)和(11))进行设计且考虑节点搭接缺陷.由图可知,可靠度指标均随着荷载效应比的增大而降低.按照我国规范[4]中的分项系数计算得出的可靠度指标β高于模板支架的目标可靠度指标βT,且节点搭接缺陷会降低模板支架的安全性水平;按照本文方法得到的可靠度指标β则与目标可靠度指标βT具有最佳一致性.
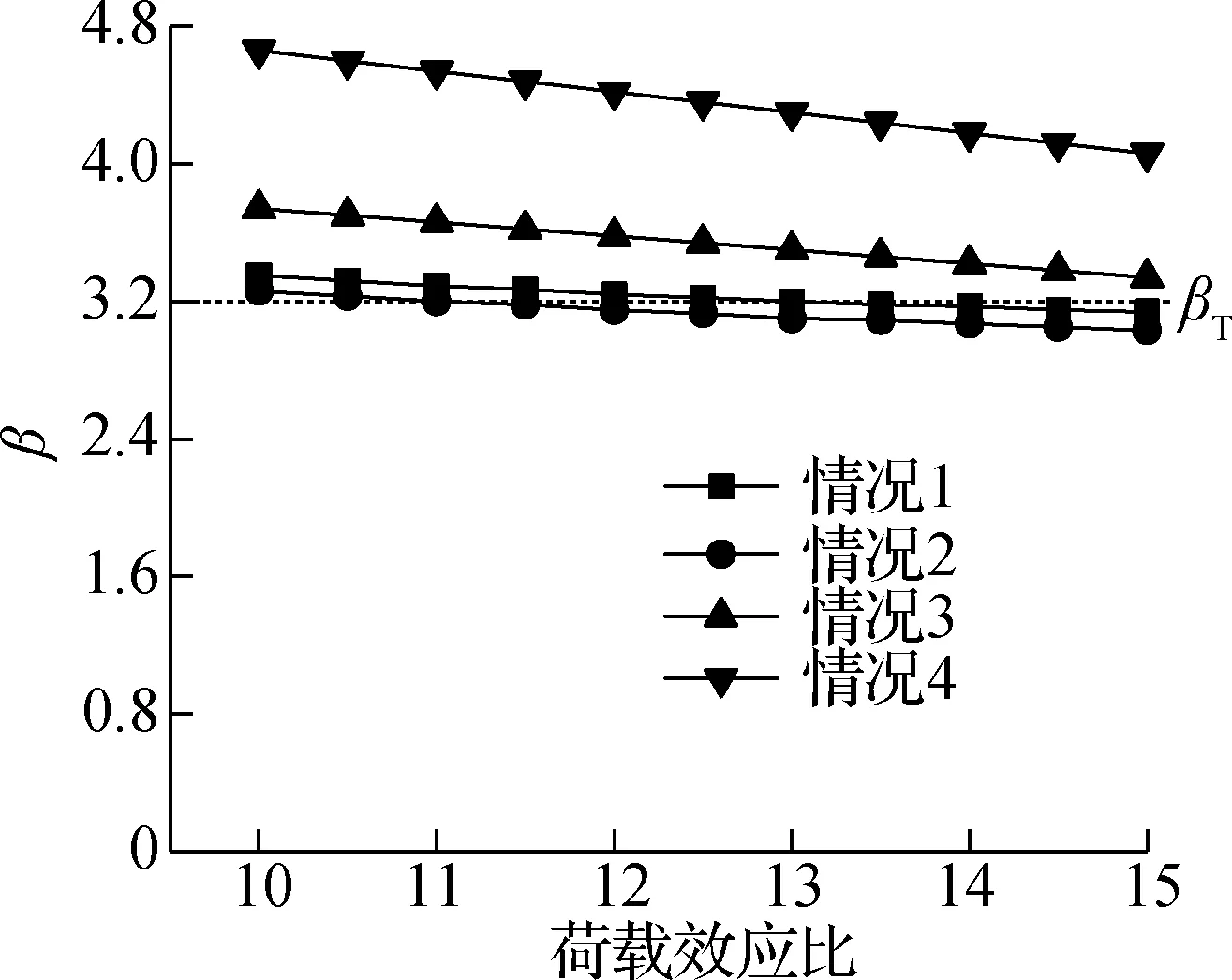
图6 模板支架可靠度指标
5 结论
1) 在混凝土浇筑前,通过施工现场调研,得到主次龙骨以及主龙骨与U形托之间的节点搭接缺陷的发生规律和统计特性.
2) 提出了一种非线性随机有限元模拟方法.该方法能够考虑模板支架上部的节点搭接缺陷,具有较高的精度.节点搭接缺陷存在时,施工荷载对荷载效应系数的影响大于支架跨数的影响.
3) 考虑节点搭接缺陷时,与目标可靠度指标具有最佳一致性的分项系数为γGE=1.2,γQE=1.9,γRE=1.7.不考虑节点搭接缺陷时,与目标可靠度指标具有最佳一致性的分项系数为γG=1.2,γQ=1.55,γR=1.7.
4) 节点搭接缺陷会降低按照我国规范[4]设计的模板支架的安全性水平.
