基于拉压杆模型的ECC深梁受剪承载力分析

2021-08-06胡世翔潘金龙

东南大学学报（自然科学版） 2021年4期

罗敏胡世翔潘金龙

(1 东南大学土木工程学院，南京 211189)(2 南京工程学院土木工程与智慧管理研究所，南京 211167)

钢筋混凝土(RC)深梁具有刚度大、承载力高、抗震性能好等优点，广泛应用于高层建筑、复杂基础工程和桥梁工程中.一般情况下，RC深梁承受的剪力值较大而弯矩值较小，容易发生脆性剪切破坏.为提高RC深梁的受剪承载力，学者们提出了一系列改进措施，如增大截面尺寸、提高混凝土强度、增大钢筋配筋量和采用新型混凝土材料等[1-3].纤维增强水泥基材料ECC是一种高韧性建筑材料，由于纤维的桥连作用，ECC材料可产生多条细密裂缝，直接拉伸应变达3%以上，具有显著的拉应变硬化特征和高韧性性能[4].将ECC材料应用于深梁中作为基体材料，既能提高深梁的受剪承载力，又能提高深梁的延性.文献[5]对ECC深梁和高强混凝土深梁进行抗剪试验，发现ECC深梁发生弯剪破坏，初裂荷载、极限荷载和剪切延性相对高强混凝土深梁均有显著提高.文献[6]中的剪切试验结果表明，与RC深梁相比，ECC深梁的极限剪切强度提高了21%，且ECC深梁破坏时显示更高的延性性能，斜截面表现为细密的多裂缝开裂模式.由此可知，ECC材料能同时从强度和延性两方面改善深梁的抗剪性能，但针对ECC材料与钢筋作用机理的研究尚不充分.

深梁的高度和跨度具有相同的数量级，在集中荷载作用下其截面应力不符合平截面假定，受剪机理较浅梁更为复杂.根据深梁中力流的传递，拉压杆STM模型将深梁抽象成离散桁架模型，由混凝土压杆、纵筋拉杆和节点组成.美国规范[7-8]基于STM模型提出了RC深梁的实用受剪承载力计算公式.学者们对RC深梁的STM模型进行了大量改进[9-12]，但大多基于试验数据回归得出，不能准确计算混凝土软化效应以及分布筋配筋率的影响[13-14].Tan等[15]基于Mohr-Columb破坏准则，推导并建立了直接STM模型，准确反映了混凝土由横向拉应变引起的抗压强度软化效应.在此基础上，Zhang等[16]提出了修正的STM模型，综合考虑了纵向受拉钢筋、分布筋对受剪承载力的影响，进一步提高了预测RC深梁受剪承载力的准确性.然而，基于STM模型的ECC深梁受剪承载力理论研究尚不成熟，缺乏实用的计算公式.

本文对不同分布筋配筋率下的ECC简支深梁进行了抗剪试验，分析了纵向钢筋应变、分布筋应变及挠度随荷载的变化规律，探究了ECC深梁的破坏特性.基于Mohr-Columb破坏准则推导建立了STM1模型，基于压杆的试验结果[17]建立了STM2模型.采用美国规范ACI318-19、STM1模型和STM2模型计算ECC深梁受剪承载力，并与试验结果进行对比，以验证本文模型的有效性.

1 试验

根据美国规范ACI318-19中的STM模型，设计了3根具有不同分布筋配筋率的ECC深梁BE1、BE2、BE3，其分布筋配筋率分别为0、0.31%、0.63%.深梁的横截面尺寸均为100 mm×450 mm，长度为1 100 mm，剪跨比为1，具体配筋如图1所示.为防止局部受压破坏，在加载点和支座处配置了局部加强短筋.

为研究钢筋的应变规律，测量了3根深梁的底部纵筋和顶部架立筋的应变，以及水平分布筋H21、H31～H33和竖向分布筋V21、V22、V31～V34的应变.试件配筋及应变片布置见图1.

(a) 深梁BE1

(b) 深梁BE2

底部纵筋采用HRB400钢筋，实测屈服强度平均值为425 MPa，屈服应变平均值为2.024×10-3.架立筋、水平分布筋和竖向分布筋采用HPB300钢筋，实测屈服强度平均值为321 MPa，屈服应变平均值为1.529×10-3.ECC材料中，水泥与粉煤灰的质量比为4，水胶质量比为0.25，国产聚乙烯醇纤维体积掺量为2%，ECC材料实测抗压强度平均值为39.9 MPa，初裂抗拉强度平均值为4.0 MPa，极限抗拉强度平均值为5.1 MPa.

ECC深梁为简支梁，试验装置如图2所示.加载处垫板尺寸为200 mm×100 mm×25 mm，支座垫板尺寸为150 mm×100 mm×25 mm.采用YAW-5000F型微机控制电液伺服压力试验机对深梁进行集中力加载.深梁达到峰值荷载前，采用力控制加载，加载速率为1 kN/s，控制目标值为每级50 kN.深梁达到峰值荷载后，采用位移控制加载，加载速率为0.05 mm/min.在深梁跨中设置位移计测量跨中挠度.通过东华3818型动静态数据采集仪采集应变和位移数据.

图2 试验装置示意图(单位：mm)

2 试验结果与分析

2.1 深梁破坏形态

ECC深梁的裂缝分布见图3.由图可知，深梁BE1、BE2的破坏过程基本相似：加载时深梁底部跨中首先出现较多弯曲正裂缝；随着荷载的增加，深梁腹部出现枣核状斜裂缝，且正裂缝不再升高；荷载继续增加，斜裂缝逐渐向加载点和支座处延伸，形成八字裂缝；达到极限荷载时，斜裂缝宽度突然增大，试件破坏.深梁BE1、BE2的极限承载力分别为1 446和1 493 kN.

(a) 深梁BE1

(b) 深梁BE2

对于深梁BE3，开始加载时，加载点下方出现较多细密裂缝；随着荷载的增加，跨中出现正裂缝；荷载增加至450 kN时，梁高1/2处开始出现斜裂缝，且裂缝中间大两端小，呈枣核状；荷载达到700 kN时，加载点下方ECC材料明显隆起，呈撕裂状；试件破坏表面有2条明显的八字斜裂缝，正裂缝数目较少，加载点处ECC材料严重压溃.深梁BE3的极限承载力为943 kN.

2.2 纵筋应变

ECC深梁中纵筋分为底部纵筋和顶部架立筋2类.荷载-纵筋应变曲线见图4.由图可知，深梁BE1和BE2的纵筋应变发展规律类似：底部纵筋的应变随荷载增加而增加，最大应变值小于其屈服应变2.024×10-3，说明底部纵筋未屈服，拉杆没有破坏.顶部架立筋应变的绝对值始终小于其屈服应变1.529×10-3，顶部架立筋亦未屈服，且加载点处仅出现少许裂缝，说明节点未发生破坏.最终破坏时，深梁BE1和BE2中均出现劈裂斜裂缝，破坏模式均属于压杆破坏.

图4 ECC深梁的荷载-纵筋应变曲线

对于深梁BE3，底部纵筋的拉应变值始终小于钢筋屈服应变2.024×10-3，说明底部纵筋未屈服，拉杆没有破坏.刚开始加载时顶部架立筋的应变为压应变；随着荷载的增加，加载点处出现较多裂缝，顶部架立筋的应变逐渐转为拉应变；当荷载继续增加时，顶部架立筋的应变值大于其屈服应变1.529×10-3，且深梁BE3加载点处ECC材料被严重压溃.结合图3(c)可知，深梁BE3的破坏模式属于节点破坏.

2.3 分布筋应变

ECC深梁中的分布筋包括水平分布筋和竖向分布筋2类.图5为深梁BE2的荷载-分布筋应变曲线.由图可知，当荷载小于650 kN时，深梁BE2中的分布筋几乎不承担荷载作用.当荷载大于650 kN时，分布筋的应变随荷载增加而增加.当试件破坏时，水平分布筋H21的最大应变仅为0.735×10-3，小于其屈服应变1.529×10-3，说明水平分布筋未屈服；竖向分布筋V21、V22的最大应变均大于其屈服应变1.529×10-3，说明竖向分布筋均达到屈服状态.与水平分布筋相比，竖向分布筋的应变值更大，能发挥更大的抗剪作用.

图5 深梁BE2的荷载-分布筋应变曲线

深梁BE3的荷载-分布筋应变曲线见图6.由图6(a)可知，深梁BE3的水平分布筋H31～H33的应变随荷载增加而增加，其中水平分布筋H33最靠近加载点，应变增幅最大，最大应变值为3.862×10-3，远大于其屈服应变1.529×10-3，说明水平分布筋H33已屈服.然而，水平分布筋H31、H32的应变值均小于其屈服应变，尚处于弹性变形阶段.与水平分布筋H32相比，水平分布筋H31更靠近深梁底部，故其应变值略大.

(a) 水平分布钢筋

(b) 竖向分布钢筋

深梁BE3中荷载-竖向分布筋应变曲线见图6(b).由图可知，竖向分布筋V33、V34靠近加载点，刚开始加载时，二者的应变值很小，当荷载大于850 kN时，应变值迅速增加，并最终超过分布筋的屈服应变，达到屈服.而竖向分布筋V31、V32则远离加载点，二者的应变值随荷载的增加而略微增加，最大应变值仅为0.721×10-3，远小于其屈服应变.

2.4 荷载-挠度曲线

ECC深梁的荷载-挠度曲线见图7.由图可知，加载初期，荷载与挠度呈线性关系；随着荷载的增大，荷载与挠度呈非线性关系.ECC深梁荷载-挠度曲线均具有明显的屈服变形平台，由于ECC材料显著的拉应变硬化性能和优越的裂缝控制能力，曲线呈现出荷载不增加而挠度持续增加的延性特征[18].

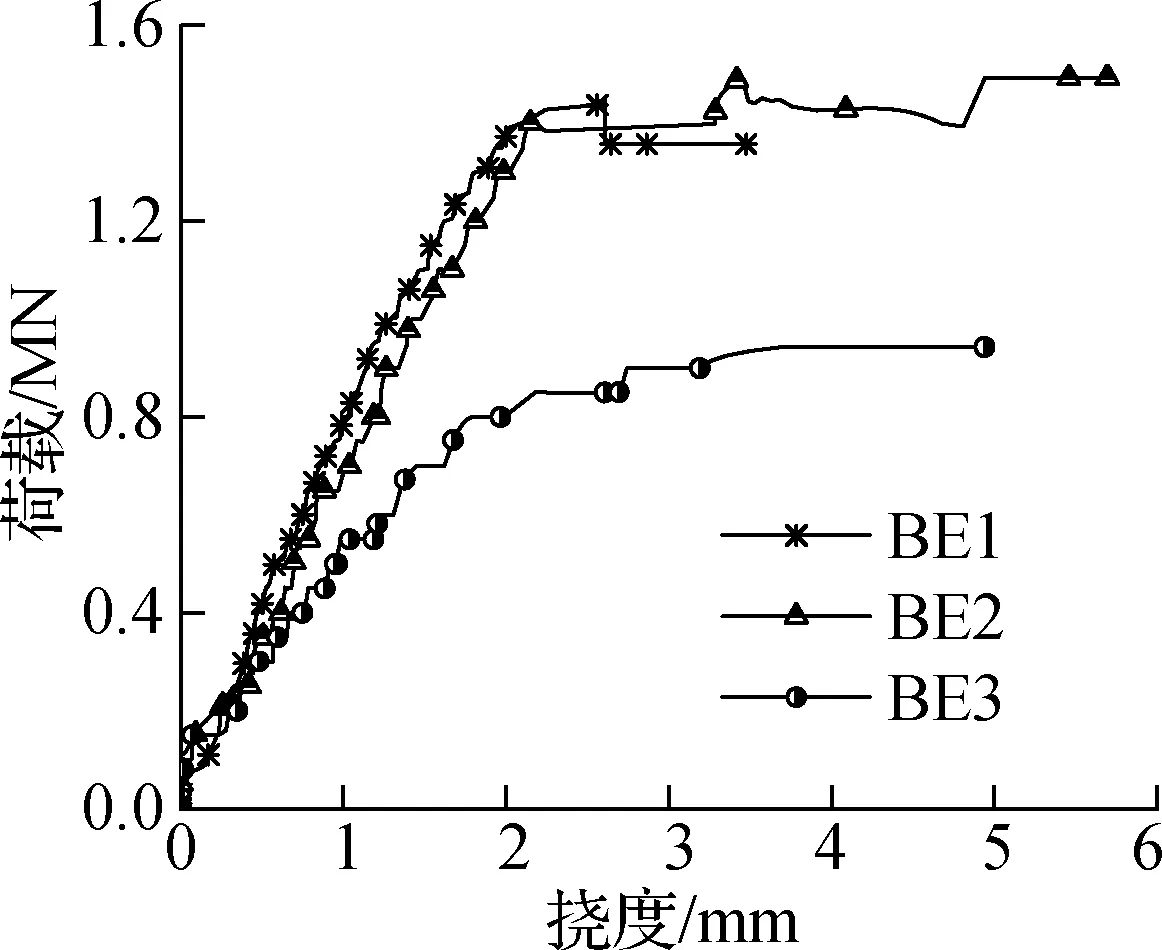
图7 ECC深梁的荷载-挠度曲线

对比深梁BE1和BE2的荷载-挠度曲线可知，分布筋配筋率从0增加到0.31%时，ECC深梁的峰值荷载仅增加了3.25%，受剪承载力则未出现显著增加，试验结果与文献[19-20]的结论一致.分布筋配筋率为0.63%时，深梁BE3的峰值荷载小于深梁BE1和BE2，究其原因在于深梁BE3的破坏模式为节点破坏，其受剪承载力由节点强度决定.

3 ECC深梁受剪承载力模型

由试验支承条件和加载方式可知，ECC深梁的计算简图为跨中作用一个集中荷载的简支梁.本文试验结果表明，ECC深梁腹剪斜裂缝开展方向与主压应力方向一致.因此，将底部纵筋简化为拉杆，将支座与加载点连线方向的ECC材料简化为压杆，压杆与压杆相交的区域、压杆与拉杆相交的区域均简化为节点，可得ECC深梁的STM计算模型(见图8).图中，Vn为深梁的受剪承载力；f1、f2分别为节点区域的主拉应力和主压应力；Fc为斜压杆所承受的压力；Ts为拉杆承受的拉力；θs为斜压杆与拉杆的夹角.

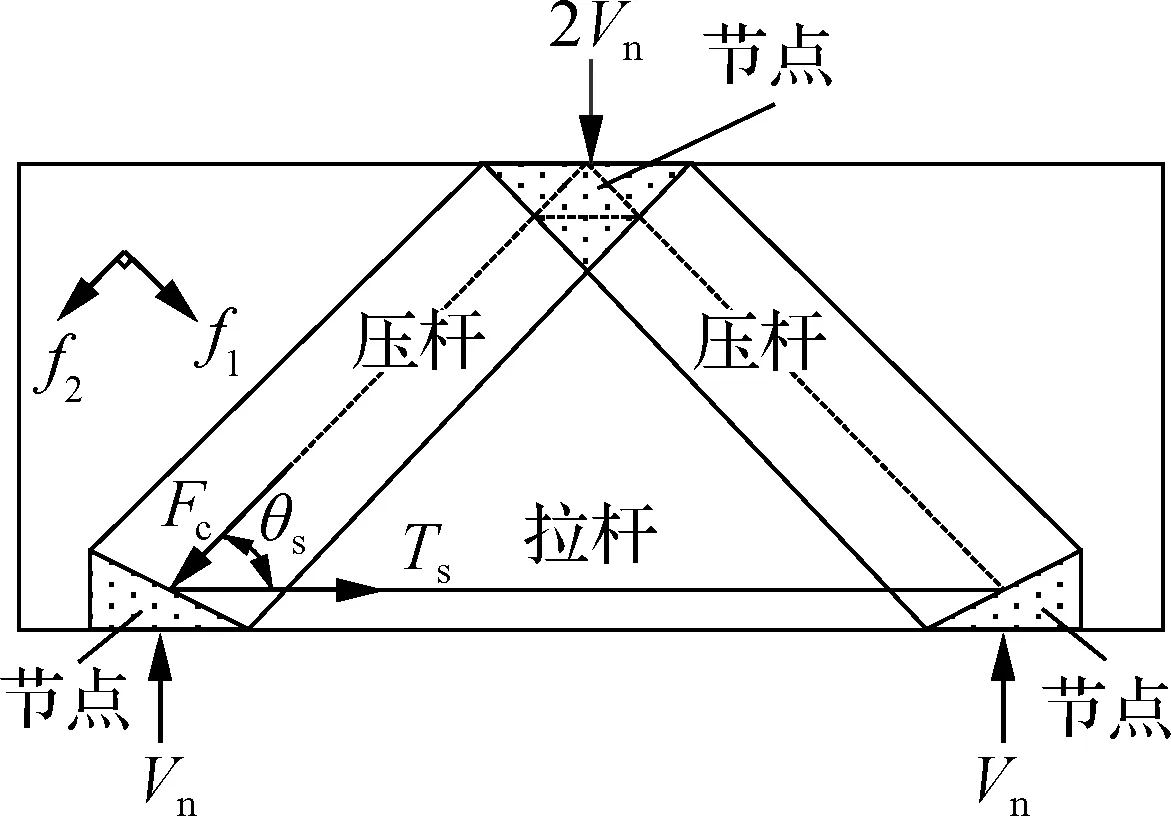
图8 ECC深梁STM模型示意图

3.1 STM 1模型

文献[16]提出的修正STM模型是基于应力破坏准则建立的，能综合考虑混凝土软化效应、纵筋和分布筋配筋率对深梁受剪承载力的影响[21]，适用于拉杆或压杆破坏模式的深梁，不适用于节点破坏.图9为等效拉应力分布原理.图中，h为深梁的截面高度；a为剪跨段长度；la、ld分布为顶部节点区的宽度和高度；lb、lc分别为底部节点区的宽度和高度；dc为深梁截面有效高度；T为钢筋中的拉力；θw为钢筋与水平线的夹角；dw为钢筋与斜压杆轴线的交点距离深梁顶部的距离；pt为拉力T在垂直于斜压杆轴线方向上的平均等效拉应力；k、k′分别为斜压杆底部和顶部节点区的应力图形分布系数.结合图8和图9，可推导出ECC简支深梁的受剪承载力公式，建立STM1模型，以计入ECC材料的抗拉强度和分布筋对ECC深梁受剪承载力的贡献.

图9 等效拉应力分布原理图

基于Mohr-Columb破坏准则，支座处节点区的应力关系为

(1)

式中，ft为沿主拉应力方向的节点区复合抗拉强度；f′c为ECC材料的圆柱体抗压强度.

结合图8，根据斜压杆底部节点的力平衡关系可得

(2)

(3)

根据几何尺寸关系可得

(4)

(5)

3.1.1 主拉应力

假设某钢筋(分布筋或纵筋)与斜压杆相交，钢筋中产生拉力T.由于钢筋是离散的，故拉力T也是离散的.为方便计算，假设由拉力T产生的拉应力沿斜压杆呈线性分布，运用力和力矩平衡方程可获得拉力T与拉应力之间的关系，即

(6)

(7)

式中

式中，Ac为深梁有效横截面面积，且Ac=bwdc；bw为深梁横截面宽度.

由式(6)和(7)可得

(8)

主拉应力f1主要来源于纵筋在垂直于斜压杆方向的分力Tssinθs，当dw=dc，θw=0，则有k=4，因此主拉应力f1的表达式可简化为

(9)

3.1.2 复合抗拉强度

复合抗拉强度ft由底部纵筋及分布筋抗拉强度在主拉应力f1方向上的分量fss、fsw以及节点区ECC材料抗拉强度fct组成，即

ft=fct+fss+fsw

(10)

fct表征ECC材料对抗拉强度的贡献.参照钢纤维混凝土结构的计算思路[22]，将fct修正为fct=fct0(1+kfλf)，其中，kf为纤维对ECC材料抗拉强度的影响系数，此处取为0.107；λf为纤维长径比.ECC材料是一种具有应变硬化性能的高韧性材料，开裂后其拉应力仍能随应变增加而增加[23].根据ECC材料的受拉本构关系，保守取fct0为ECC材料的初裂抗拉强度.

fss表征纵筋对抗拉强度的贡献.由式(9)可得

(11)

式中，fy为底部纵筋的屈服强度；As为底部纵筋的横截面总面积.

fsw表征分布筋对复合抗拉强度ft的贡献.尽管分布筋是离散的，但分布筋能限制斜裂缝向斜压杆两端快速发展，故仍需考虑其在节点与斜压杆界面处的作用.在ECC深梁中，假设存在ns根分布筋沿斜压杆均匀分布，则其应力分布系数为

(12)

则有

(13)

式中，fyw为分布筋的屈服强度；Asw1为单根分布筋的横截面面积.

3.1.3 主压应力

考虑拉杆分力对深梁受剪承载力的有利影响，节点区的主压应力f2可表示为

(14)

式中，Astr为斜压杆的横截面面积，且Astr=bw(lccosθs+lbsinθs).

将式(2)、(3)代入式(9)、(14)，结合式(1)可得深梁的受剪承载力Vn为

(15)

(16)

3.1.4 计算步骤

综上可知，STM1模型的计算步骤如下：

①首次迭代时假设l1=lc，由式(4)可计算得到θs.

③迭代结束时，利用式(15)计算ECC深梁的受剪承载力.

3.2 STM 2模型

根据美国规范ACI 318-19中第23.4条，可得斜压杆的名义承载力Fns为

Fns=0.85βcβsf′cAstr

(17)

式中，βc为压杆的约束修正系数；βs为压杆有效系数，对于RC深梁，βs根据压杆的受力和边界情况取值为0.40、0.75或1.00，即通过大量试验回归分析得出的经验值[24-25].

借鉴RC深梁压杆有效系数βs的试验研究方法，参照文献[17]，对不同分布筋配筋率下的ECC压杆进行试验.试验结果表明，对于ECC深梁，分布筋配筋率为0时βs=1.63，分布筋配筋率为0.31%时βs=1.86.将βs代入式(17)，可计算得到ECC深梁的受剪承载力Vn为

Vn=Fnssinθs=0.85βcβsf′cAstrsinθs

(18)

4 计算结果分析

采用本文中的ECC深梁及文献[6]中试验梁U0.7-0和U0.7-0.2的试验数据验证STM1模型和STM2模型的有效性，并与基于ACI318-19中计算方法所得结果进行对比，结果见表1.表中，Vexp为ECC深梁受剪承载力的试验值；VSTM、VSTM1、VSTM2分别为根据ACI318-19中计算方法、STM1模型、STM 2模型得到的ECC深梁受剪承载力计算值.

表1 ECC深梁受剪承载力计算值与试验值对比

由表1可知，根据ACI318-19中计算方法、STM1模型、STM 2模型得到的ECC深梁受剪承载力计算值与试验值比值的均值分别为0.42、0.87、0.82，标准差分别为0.10、0.12、0.05.由此可知，ACI318-19中计算方法低估了ECC深梁的受剪承载力；STM2模型计算过程简便，可快速地预测ECC深梁的受剪承载力，但只适用于分布筋配筋率为0或0.31%的ECC深梁；STM1模型的计算值与试验值吻合程度最高，能准确预测不同分布筋配筋率下ECC深梁的受剪承载力.