基于核密度估计的干接缝装配式桥墩概率性地震损伤特性分析
2021-08-06冯梦瑶马馨怡
江 辉 李 辰 冯梦瑶 罗 萌 马馨怡
(1北京交通大学土木建筑工程学院, 北京 100044)(2中国铁道科学研究院高速铁路轨道技术国家重点实验室, 北京 100081)(3民航机场规划设计研究总院有限公司, 北京 100101)
相比于整体现浇结构,装配式结构具有建造速度快、预制构件质量高、节能环保、对环境干扰小等优点,近年来逐渐应用于高速公路、市政道路及跨江跨海桥梁中,如上海S26公路、成都羊犀立交、港珠澳大桥等.
干接缝预制拼装桥墩的纵筋于接缝处断开,节段通过后张预应力筋连接,施工方便且震后易于快速修复.由于节段间接缝的存在,其抗震性能相较于整体现浇墩势必存在差异.Mander等[1]对干接缝预应力摇摆墩开展了拟静力试验研究,发现此类桥墩具有良好的自复位能力.Dawood等[2]探讨了初始张拉应力、轴压比、长细比等因素对拼装桥墩抗震性能的影响规律,并给出了各参数的合理取值范围.Zhang等[3]研究了混凝土强度、预应力筋配筋率、初始预应力水平等参数的影响规律,发现预应力筋配筋率和初始预应力水平对桥墩屈服后刚度影响显著.李辰[4]分析了预应力筋配筋率、节段参数及剪力键参数的影响规律,结果表明提高预应力筋配筋率可显著增大桥墩抗剪能力和耗能能力.既有研究主要围绕不同参数对干接缝拼装桥墩抗震性能的影响规律展开,如何量化地震作用下各参数影响程度的研究则较少.此外,当前研究成果均未考虑地震动不确定性的影响,难以对预制拼装桥墩形成定量、全面的认识.
地震易损性分析可从概率角度量化结构在不同地震动水平下发生损伤的概率,对评估结构的抗震安全性具有重要意义.Shinozuka等[5]采用易损性分析,确定了Northridge地震中2座受损连续梁桥的加固等级.Wu等[6]基于增量动力分析法(IDA)开展了中等跨径斜拉桥的地震易损性分析,明确了该桥的易损部位及损伤程度.江辉等[7]通过地震易损性分析量化了氯离子腐蚀环境下近海斜拉桥主要构件的损伤概率.基于核密度估计(KDE)的易损性分析法,克服了参数估计法需假定易损性函数分布形式的不足,具有更高的精确性和适用性.Mai等[8]基于KDE法研究了3层钢结构的地震损伤特性,发现基于KDE法与蒙特卡洛法计算的易损性曲线基本一致,且KDE法效率更高.单德山等[9]以某铁路刚构-连续组合体系桥梁为研究对象,系统对比了参数估计法和非参数估计法的易损性分析结果,得到了类似结论.开展预制拼装桥墩基于KDE的易损性分析,可全面了解结构破坏性能、量化可变因素的影响程度,弥补当前研究的不足.
本文以某城轨高架桥为背景,选取干接缝预制拼装桥墩为研究对象,基于OpenSEES数值计算平台建立精细化纤维模型,与既有试验结果进行对比,验证模拟方法的可靠性.在此基础上,通过IDA分析和基于KDE法的地震易损性分析,揭示不同地震动强度下预制拼装桥墩的损伤特征,明确关键参数对桥墩抗震性能的影响规律与水平,并与同尺寸整体现浇墩进行对比,为预制拼装桥墩的推广应用提供理论参考.
1 基于KDE法的地震易损性分析
当前,地震易损性分析以基于数值模拟建立易损性曲线的理论分析为主,其具体方法大致可分为参数估计和非参数估计两大类.参数估计法可简化计算,但人为假设易损性函数分布形式的有效性仍需探讨.非参数KDE法无需对数据的分布形式进行任何假设,即可实现对密度函数的估计[10].基于KDE法的易损性分析引入了条件概率密度函数,其计算过程为:采用KDE法得到边缘密度函数和联合密度函数,计算条件概率密度函数,通过数值积分得到地震易损性的超越概率,即
P(a,C)=P(D≥C|IM=a)=
(1)
式中,P为地震作用下结构发生损伤的超越概率;D为结构地震需求;C为结构抗力;IM为地震动强度;a为地震动强度值;c为地震动激励下结构动力响应值;fD(c|IM=a)为结构抗力的条件概率密度函数,且
(2)
式中,fIM(·)为地震动强度IM的边缘概率密度函数;fD,IM(·)为地震动强度IM与结构抗力C所对应分布的联合概率密度函数.
一维随机变量的KDE法定义为:假设x1、x2、…、xn为变量x服从独立同分布F的n个样本点,则其概率密度函数为
(3)
式中,K(x)为核函数,通常选用高斯核函数;h为带宽参数,影响概率密度函数的精确性及光滑程度,其计算方法包括拇指法则和插入法等.
KDE法可实现维度拓展,估计多维随机变量的概率密度函数为
(4)
式中,H为带宽矩阵.
本文为得到干接缝预制拼装桥墩的易损性曲线,结合地震动强度与结构响应的样本对(IMi,Di)(i= 1,2,…,n),对边缘密度函数和联合密度函数进行计算.
地震动强度IMi(i=1,2,…,n)的边缘密度函数为
(5)
地震动强度和动力响应(IMi,Di)的联合密度函数为

(6)
由此可知,构件或结构基于KDE法的地震易损性超越概率为
P(a,C)=P(D≥C|IM=a)=
(7)
2 预制拼装桥墩模拟方法及验证
为保证本文数值分析结果的准确性,本节以既有干接缝桥墩拟静力试验结果为基准,验证纤维模型模拟方法的可靠性.
2.1 桥墩试件拟静力试验
Ou等[11]开展了4个无黏结预应力矩形空心截面节段拼装桥墩的拟静力试验,本文选取其中C0C试件的试验结果作为对照.如图1所示,该墩高4.5 m,墩身由4个等高节段组成,节段间采用干接缝,并通过4φ15.2 mm的1 860 MPa级预应力钢绞线连接.纵筋直径为18 mm,箍筋直径为10 mm,箍筋间距为70 mm.混凝土抗压强度为32 MPa,普通钢筋屈服强度为444 MPa.预应力轴压比为7%,恒载轴压比为10%,墩顶往复荷载采用位移加载方式,幅值依次取为试件有效高度的 ±0.25%、±0.375%、±0.5%、±0.75%、±1.0%、±1.5%、±2.0%、±3.0%、±4.0%、±5.0%.
2.2 试验桥墩有限元建模及结果对比
采用纤维梁柱单元模拟钢筋混凝土节段.约束及非约束混凝土采用Concrete01材料(见图2(a));普通钢筋采用Reinforcing steel材料(见图2(b));预应力筋采用桁架单元模拟并配以Steel02材料(见图2(c));承台和盖梁均采用弹性梁单元模拟.
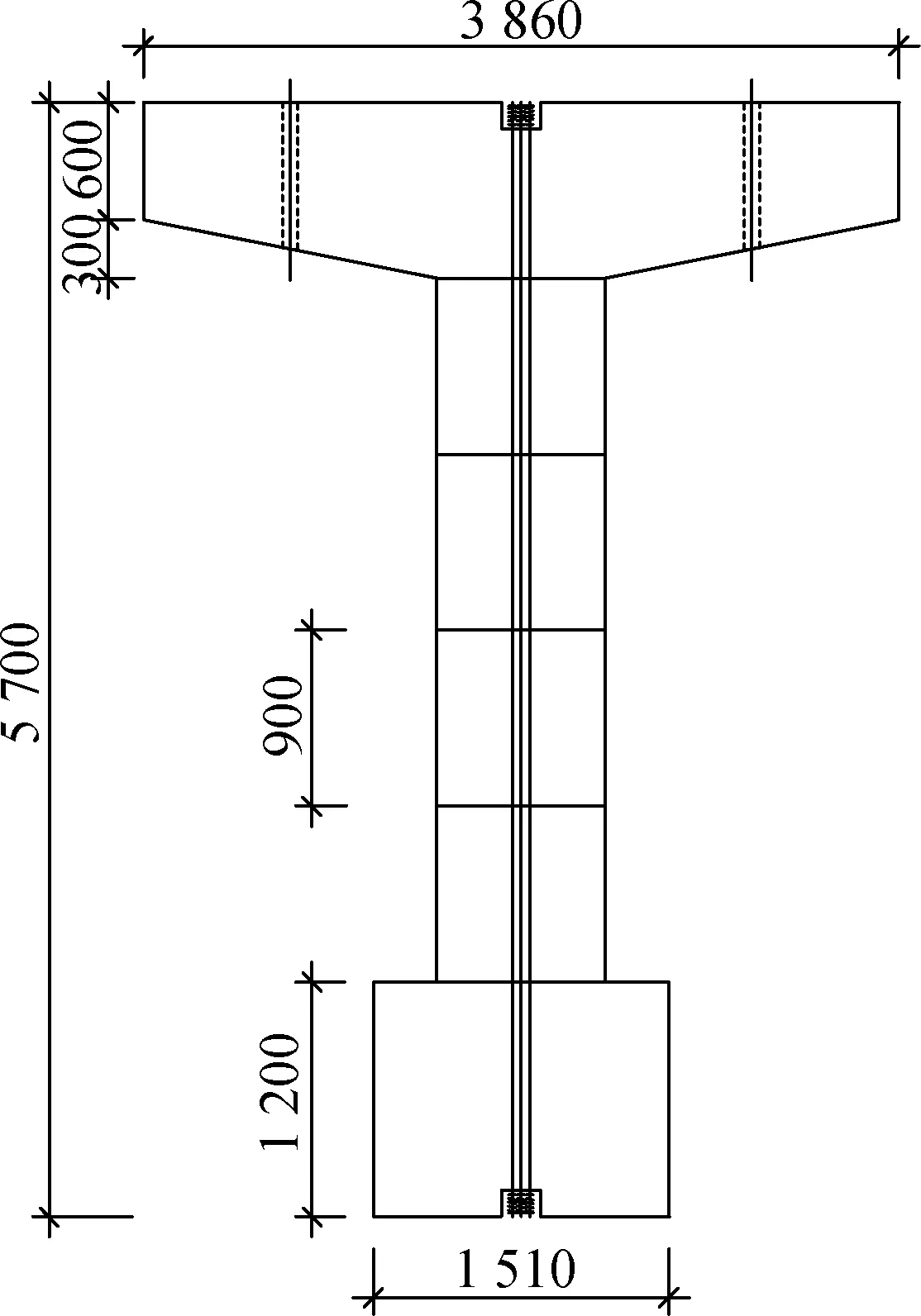
(a) 正立面图
节段间接触行为的模拟是建立干接缝拼装桥墩有限元模型的关键,主要有以下3种方式:① 将接缝区域等效为等高的素混凝土柱,并修正接缝区混凝土抗压强度[12],此方法无法准确反映桥墩强度退化及局部混凝土压溃现象;②采用并联弹簧单元模拟桥墩的摇摆现象[13],由于假设的接缝受压高度恒定,故无法反映动力作用下节段间接触面积不断变化的特点;③采用零长度截面单元或布置一系列零长度单元[14],此方法模拟节段间相互作用的有效性已得到多次验证,故本文采用零长度截面单元模拟接缝.
模型承台底部固结,墩顶加载端自由;预应力筋上部与墩顶采用刚臂连接,底部固结于承台底;桥墩上部恒载采用集中质量施加于墩顶.图2(d)为试件C0C纤维模型示意图;图2(e)和(f)分别为节段和接缝处截面纤维单元划分示意图.

(a) 混凝土应力-应变关系
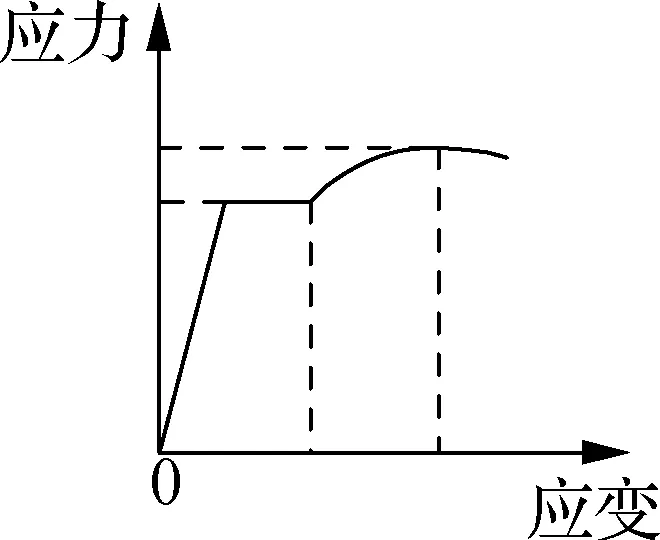
(b) 普通钢筋应力-应变关系
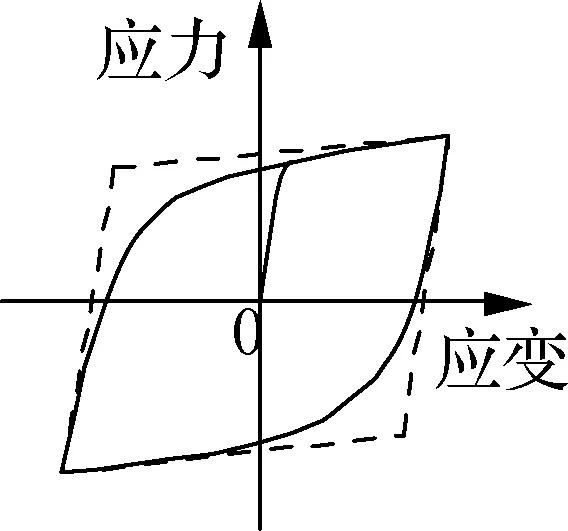
(c) 预应力筋应力-应变关系
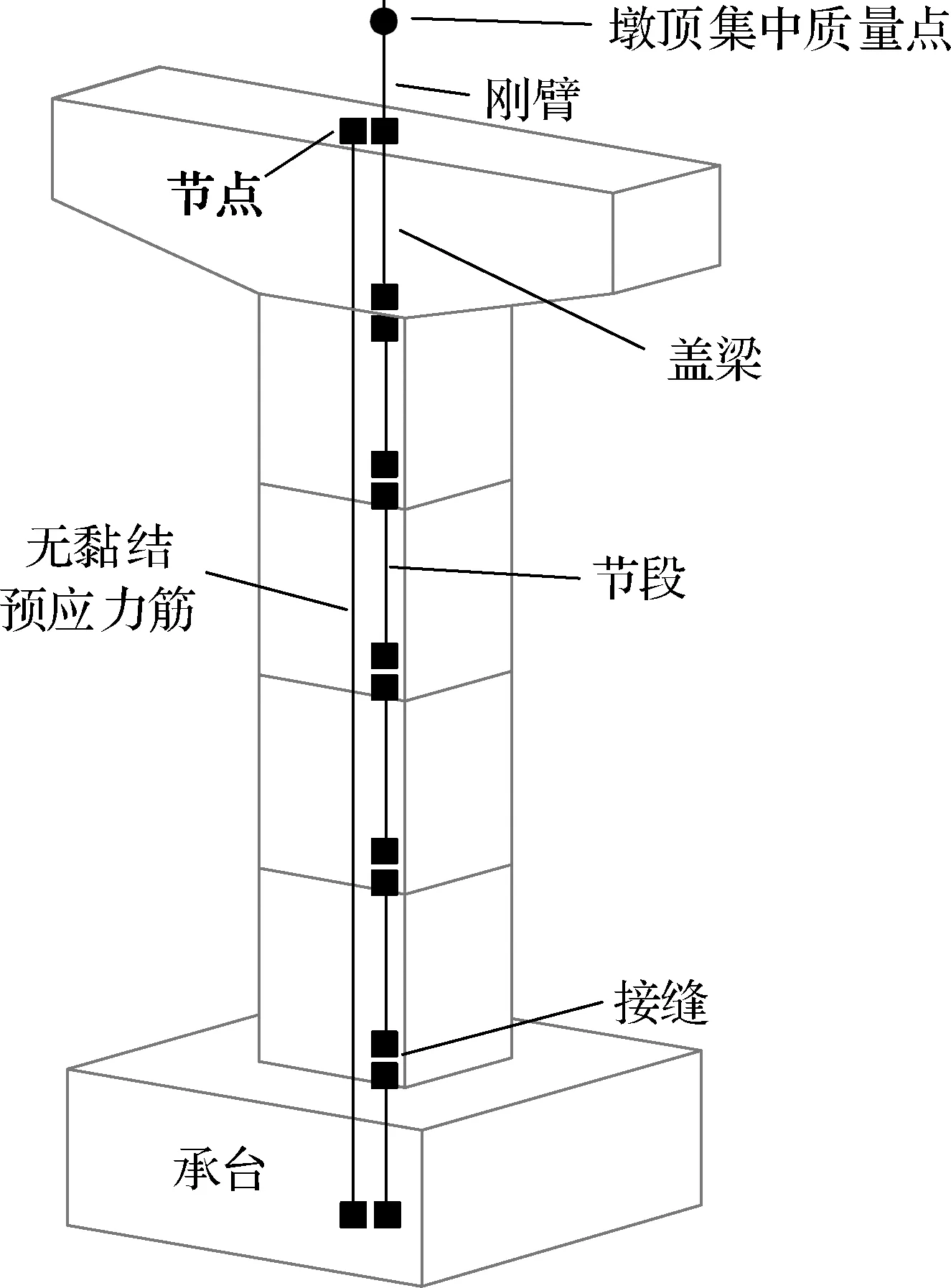
(d) 试件C0C的纤维模型
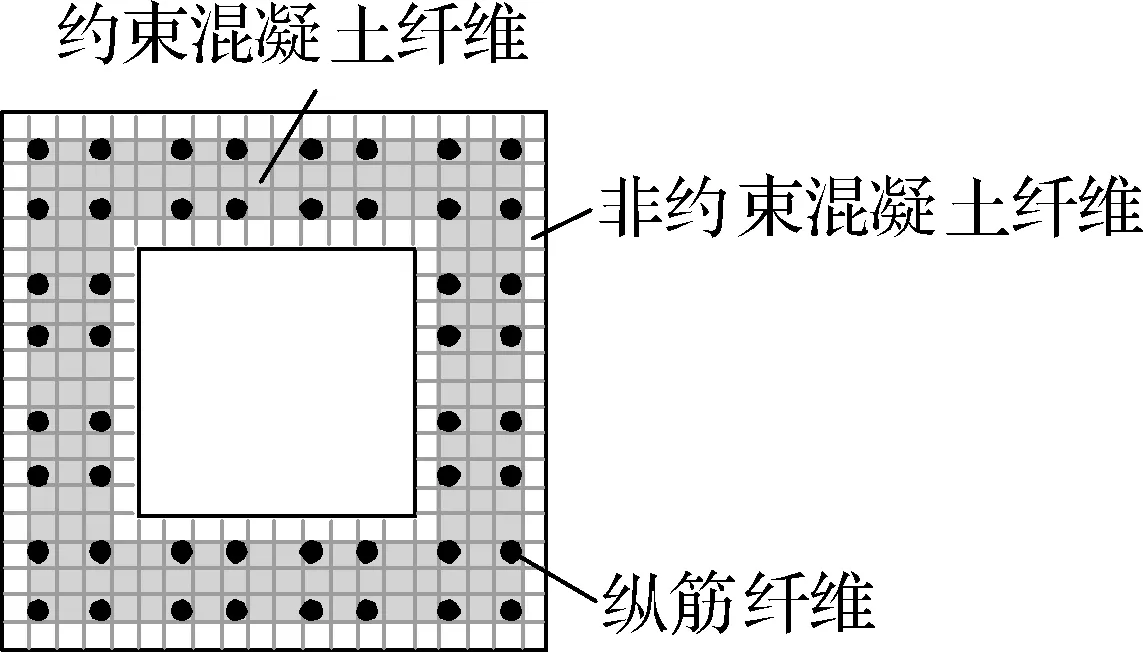
(e) 节段纤维截面
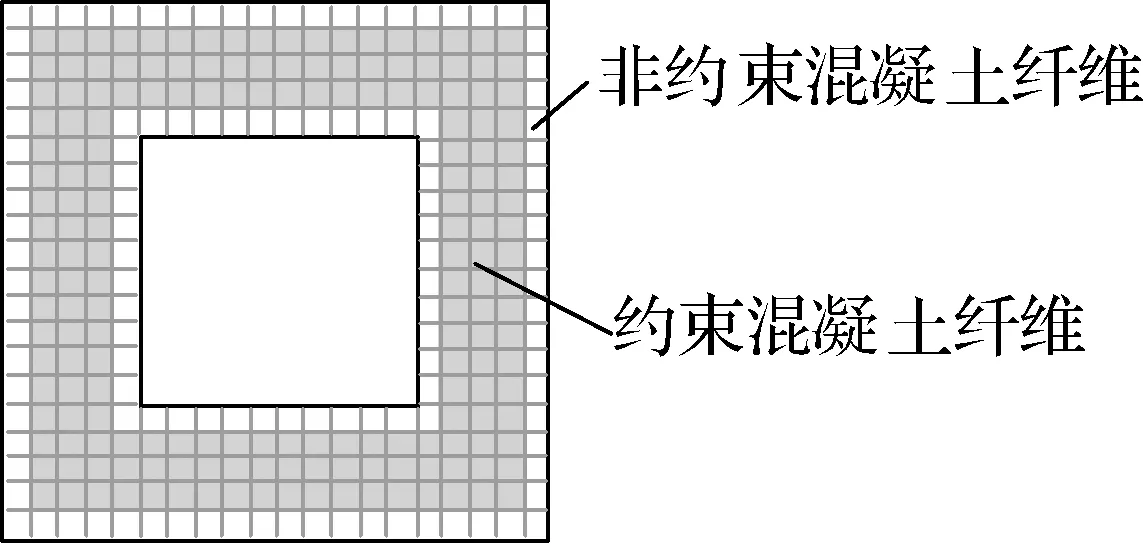
(f) 接缝纤维截面
试验与模拟所得桥墩滞回曲线对比见图3.由图可知,曲线总体形状基本一致,模拟结果的峰值荷载为257.33 kN,相较于试验结果(279.81 kN)的误差为8.09%.表1给出了底节段与承台接缝处张口宽度模拟结果相较于试验测试值的误差,可看出不同偏移率下试件墩底接缝的最大变形误差为8.37%.说明本文采用的模拟方法能较为合理地预测干接缝预制拼装桥墩的力学行为,可用于后续研究.

图3 滞回曲线
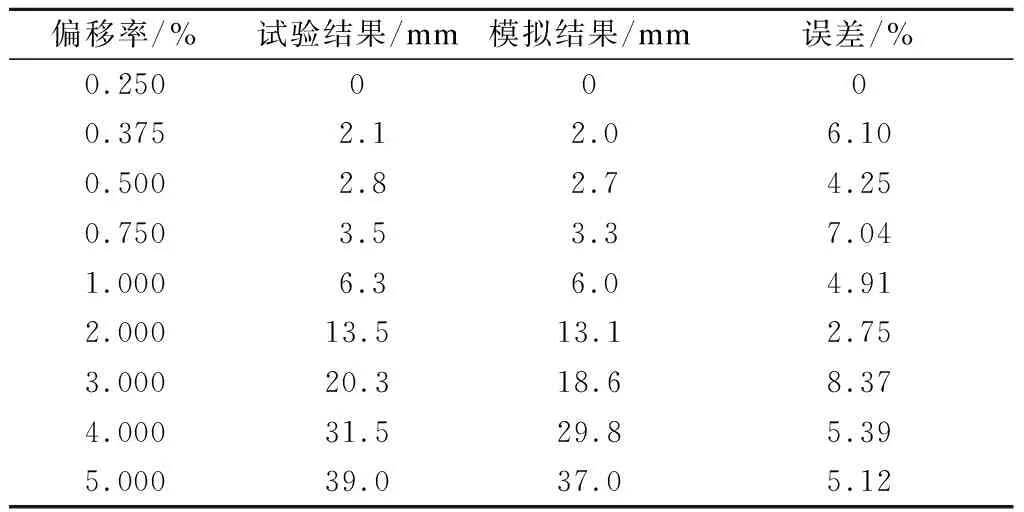
表1 不同偏移率下底接缝处张口宽度对比
3 预制拼装桥墩增量动力分析
3.1 工程概况
本文以某城市轨道交通桥梁为工程背景,该桥为跨度40 m的混凝土简支箱梁桥,矩形截面独柱墩高10 m,墩身由4个等高节段组成,并采用无黏结预应力筋将各个节段连接.墩身截面尺寸为2.4 m×2.4 m,采用C40混凝土.预应力筋为1 860 MPa级钢绞线,初始张拉应力为屈服强度的50%.纵筋全截面配筋率为0.76%,体积配箍率为 0.57%.考虑到干接缝桥墩预应力筋的耐久性问题,实际工程中可在接缝预应力孔道处及截面边缘设置2条橡胶止水带,拼接缝涂抹改性环氧树脂封缝,预应力筋采用重防腐涂料配套方案.预制拼装桥墩构造图见图4.
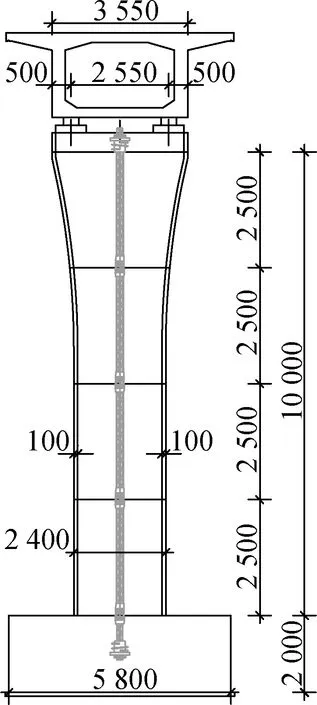
(a) 正立面图

(c) 平面图
该工程抗震设防烈度为Ⅷ度,设计基本地震动加速度为0.2g,场地类型为Ⅱ类,实测土层等效剪切波速为475 m/s.
选取单个桥墩为研究对象,考虑墩身及上部结构质量,采用第2节中的建模方法,建立其纤维模型并进行模态分析.桥墩前3阶自振周期分别为0.60、0.54、0.22 s.
3.2 地震动选取
易损性研究中,地震动主要依据空间特征、场地特征、震级和震中距、断层机制等原则进行选取[15].本文根据桥址场地特征,从美国太平洋地震工程研究中心数据库中选取150条近场地震记录用于IDA分析和地震易损性分析.具体原则如下:①断层类型为走滑断层;②断层距小于20 km;③场地剪切波速为260~510 m/s.表2和图5分别给出了所选150条地震动峰值加速度PGA分布范围以及地震动加速度反应谱.
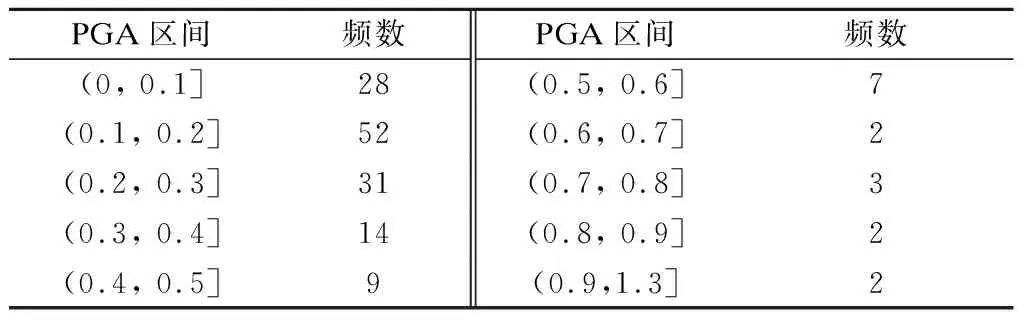
表2 所选地震动PGA分布
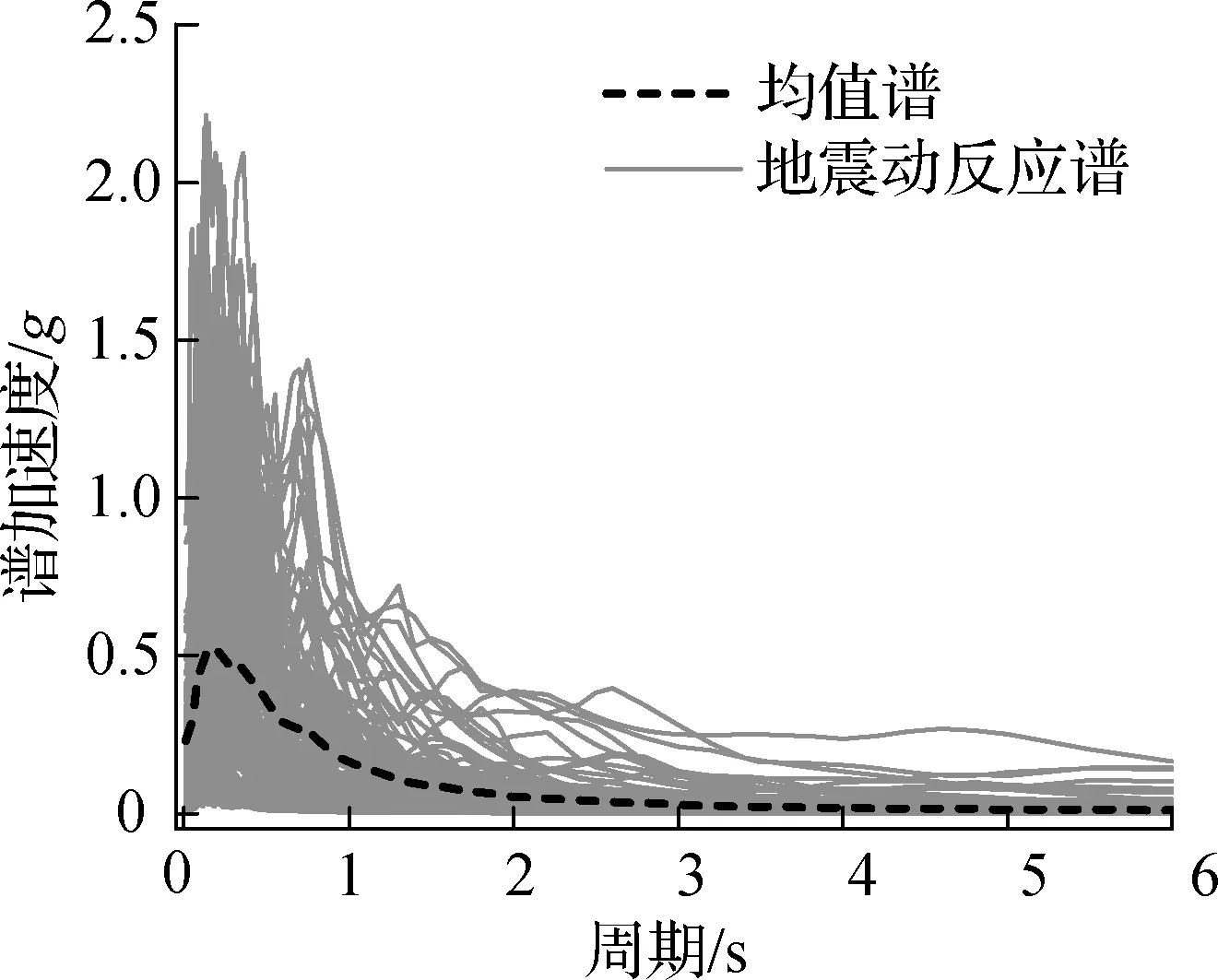
图5 所选地震动加速度谱
3.3 损伤指标及损伤水平确定
确定结构性能水平、量化损伤状态是地震易损性分析的前提,但预制拼装桥墩的相关研究较少,尚未形成统一认识.布占宇等[16]采用钢筋应变、混凝土应变、侧移率、位移延性比、预应力筋应变5种参数建立了无黏结预制拼装桥墩损伤程度与损伤状态之间的联系;王震[17]认为将位移延性比作为预制拼装超高性能混凝土空心桥墩的损伤指标是安全可行的,当PGA过大时可补充残余位移角作为破坏标志.
本文针对拼装桥墩定义了无损伤、轻微损伤、中等损伤、严重损伤、完全破坏5种损伤状态,利用位移延性比μ对预制拼装桥墩的损伤状态进行定量界定[16-17],各损伤状态及量化指标见表3.表中,μcr为桥墩底节段纵筋首次屈服时的位移延性比;μy为桥墩骨架曲线依据Park法计算得到的等效屈服位移延性比;μm为桥墩达到最大承载力时的位移延性比;μu为桥墩承载力下降至最大水平承载力85%时所对应的位移延性比.

表3 损伤状态及对应的损伤描述
以混凝土强度等级为C40、初始预应力水平为50%、墩身节段个数为4的预制拼装桥墩为例,对损伤状态界限值的量化取值进行说明.如图6所示,底节段纵筋首次屈服点、等效屈服点、最大水平承载力点和极限点对应的位移延性比分别为1、1.15、4.71、10.60.
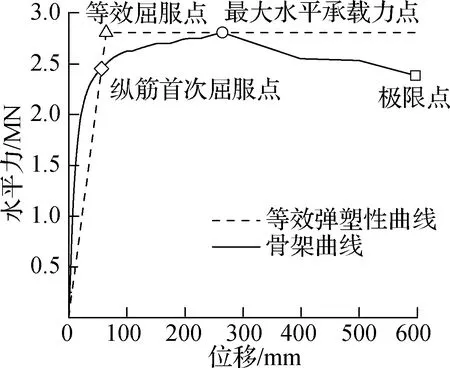
图6 桥墩特征水平位移
3.4 不同结构参数下的IDA分析
IDA分析可揭示结构在地震作用下的弹塑性变化过程,也可为后续易损性分析奠定数值基础.本文重点研究混凝土强度等级、初始预应力水平、节段个数3个参数对桥墩抗震性能的影响规律.
图7(a)为不同混凝土强度等级下预制拼装桥墩的均值IDA曲线.由图可知,当谱加速度Sa=0.7g时,C30、C40、C45、C50混凝土强度等级下IDA曲线对应的位移延性比平均值分别为9.44、7.68、6.92和6.19.随混凝土强度的提高,桥墩极限位移延性比逐渐下降,这是因为在相同轴压比和配箍条件下,混凝土强度越高,达到峰值应力后其应力-应变曲线下降越快,即混凝土的脆性表现越强,极限应变越小,宏观表现为桥墩延性降低.
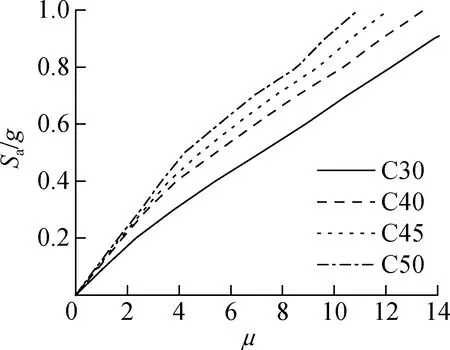
(a) 混凝土强度

(b) 初始预应力水平
(c) 节段个数
保持混凝土强度等级C40、节段个数4不变,开展不同初始预应力水平下的IDA分析,桥墩均值IDA曲线见图7(b).由图可知,桥墩位移延性比随预应力水平增加而减小,当Sa=0.6g时,预应力水平为30%、40%、50%的桥墩位移延性比均值分别为7.58、7.30、6.95.在相同轴压比下,提高预应力筋初始预应力水平需要减小预应力筋配筋率,从而导致桥墩自复位能力降低,位移延性比减小.这与文献[2]中的结论基本一致,即初始预应力水平越高的预制拼装桥墩,其预应力筋屈服时的墩顶横向位移越小.
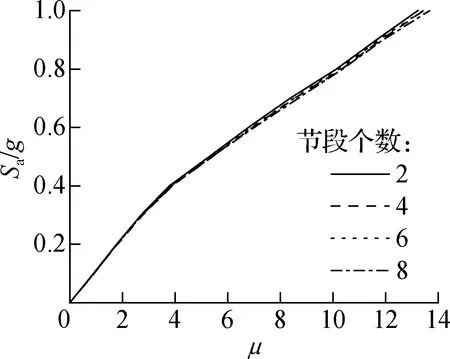
保持混凝土强度等级C40、预应力水平50%不变,开展不同节段个数下的IDA分析,桥墩均值IDA曲线见图7(c).由图可知,当Sa=0.7g时,节段个数为2、4、6、8的桥墩位移延性比平均值分别为8.47、8.53、8.52、8.60.由此说明,该研究范围内改变节段个数对结构的响应影响不大.
4 概率性地震损伤特性分析
4.1 带宽参数和带宽矩阵
确定带宽参数h和带宽矩阵H是基于KDE法计算易损性的前提,也是影响计算结果的关键因素.本文分别采用拇指法则和插入法计算边缘概率密度函数,并将结果与直方图进行对比(见图8).由图可知,采用拇指法则计算的边缘概率密度函数更能准确描述谱加速度的多峰特性.因此,选择拇指法则来计算最优带宽参数,计算公式为[18]
h=0.9Cn-1/5
(8)
(9)
式中,σ为样本标准差;Q为样本的四分位矩.
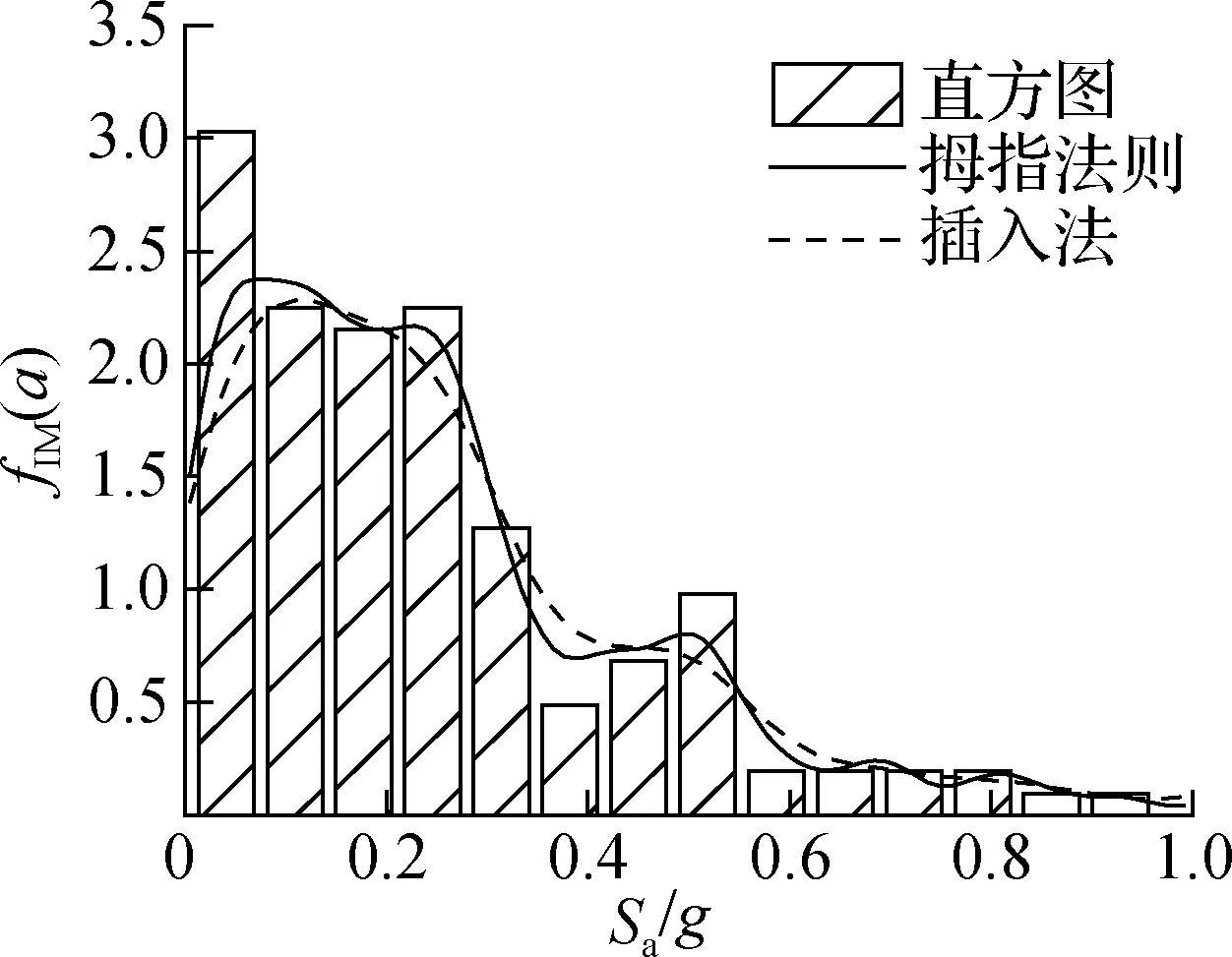
图8 谱加速度的边缘概率密度对比
对于带宽矩阵H,本文基于交叉验证法、插入法、参照法则及最平滑原则等4种方法求得带宽矩阵绘制易损性曲线,并与蒙特卡洛法计算的曲线进行对比.以混凝土强度等级为C40、初始预应力水平为50%、墩身节段个数为4的预制拼装桥墩中等损伤状态下的易损性曲线为例,图9为4种方法与蒙特卡洛法所得易损性曲线的对比图.由图可知,采用最平滑原则计算的易损性曲线与蒙特卡洛法结果吻合程度最好,故本文选择最平滑原则计算最优带宽矩阵,计算公式为[19]
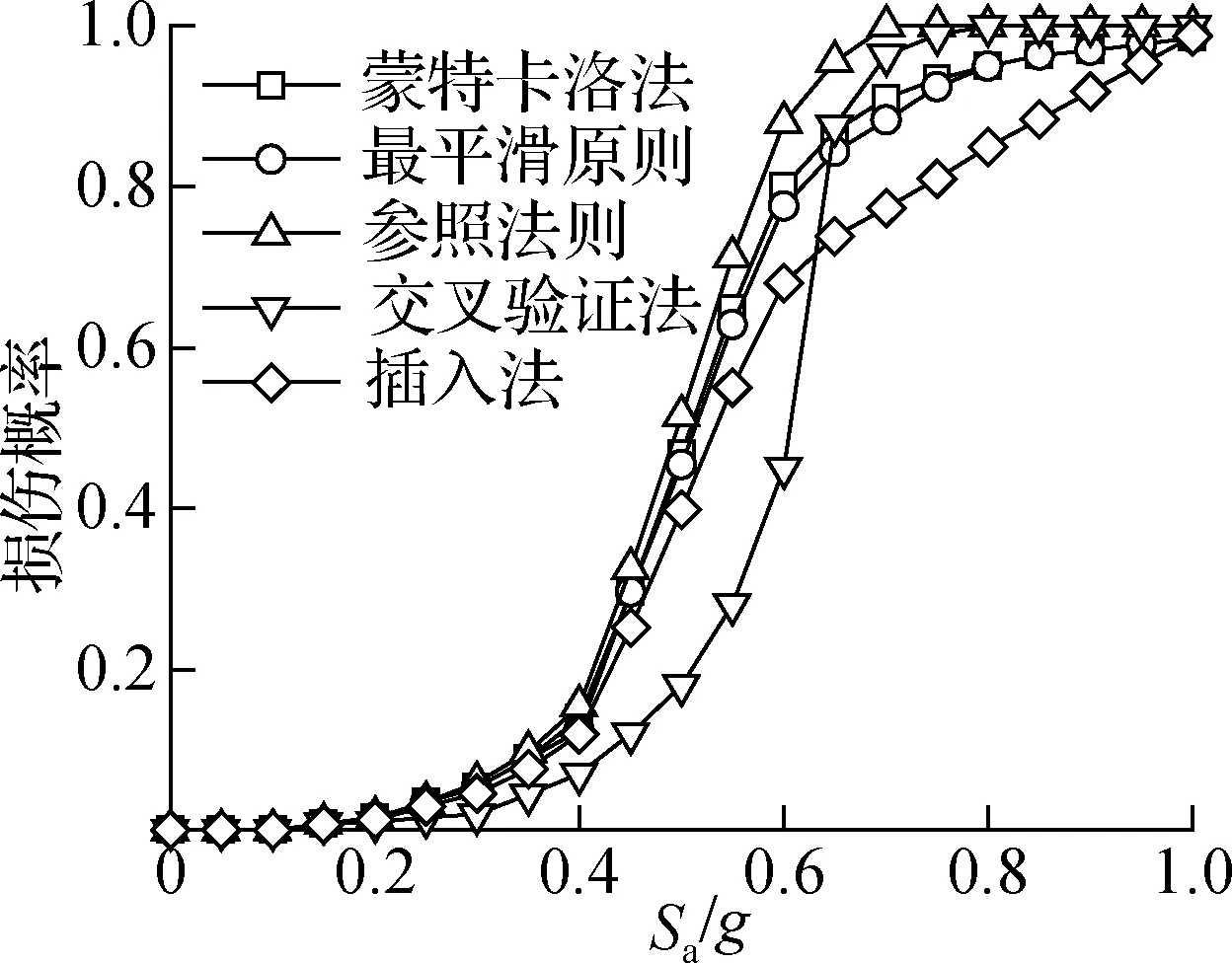
图9 不同方法计算的易损性曲线对比
(10)
4.2 混凝土强度等级的影响
基于IDA分析结果,采用KDE法计算地震动强度的边缘密度函数和地震动强度与结构响应的联合密度函数,建立相应的易损性函数,得到不同混凝土强度等级下桥墩的易损性曲线,结果见图10.由图可知,各损伤状态下的超越概率均随谱加速度Sa的增大而增大.在C30、C40、C45、C50混凝土强度等级工况下,桥墩轻微损伤的超越概率分别在Sa=0.20g、0.28g、0.37g、0.40g时达到100%,桥墩严重损伤的概率在Sa=0.5g时分别为 69.1%、55.5%、47.8%、41.9%.在相同轴压比和配箍条件下,提高混凝土强度可增加桥墩截面承载力,降低结构发生损伤的概率.对于完全破坏状态,C50混凝土桥墩完全破坏的发生概率逐渐增大,甚至超过其他3种桥墩的破坏概率.例如,当Sa=0.9g时,C30、C40、C45、C50混凝土强度等级工况下,混凝土桥墩发生完全损伤的概率分别为64.7%、54.9%、49.0%、70.9%.究其原因在于,混凝土强度越高,其应力-应变关系在达到峰值应力后下降越快,脆性表现越明显,导致桥墩的极限变形能力和延性性能越差,越容易发生完全破坏.
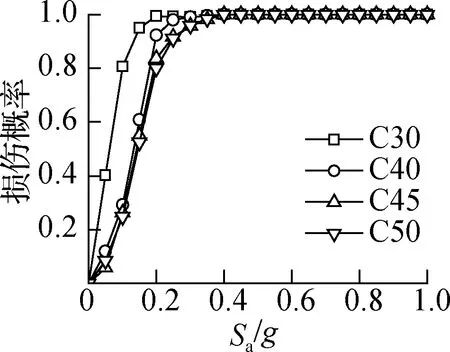
(a) 轻微损伤

(c) 严重损伤
4.3 初始预应力水平的影响
图11给出了桥墩在不同初始预应力水平下的易损性曲线.由图可知,当Sa=0.2g时,初始预应力水平为30%、40%、50%的桥墩发生轻微损伤的概率分别为93.6%、93.7%、92.3%.当Sa=0.4g时,中等损伤的发生概率均为100%,轻微损伤、中等损伤状态的超越概率随初始预应力水平的增加变化不明显.
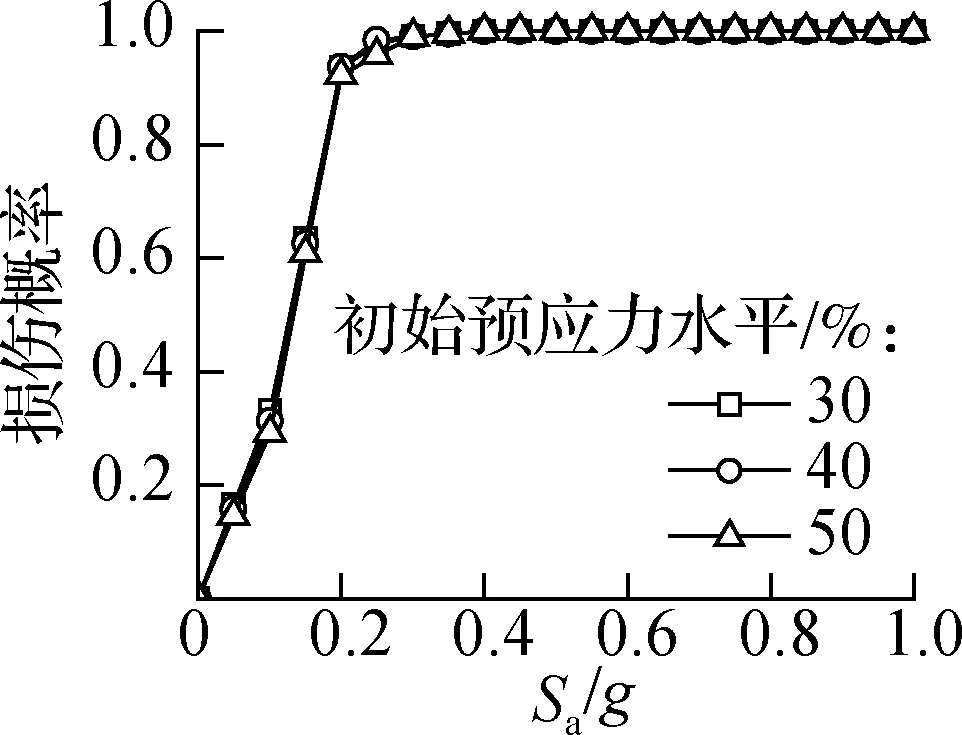
(a) 轻微损伤
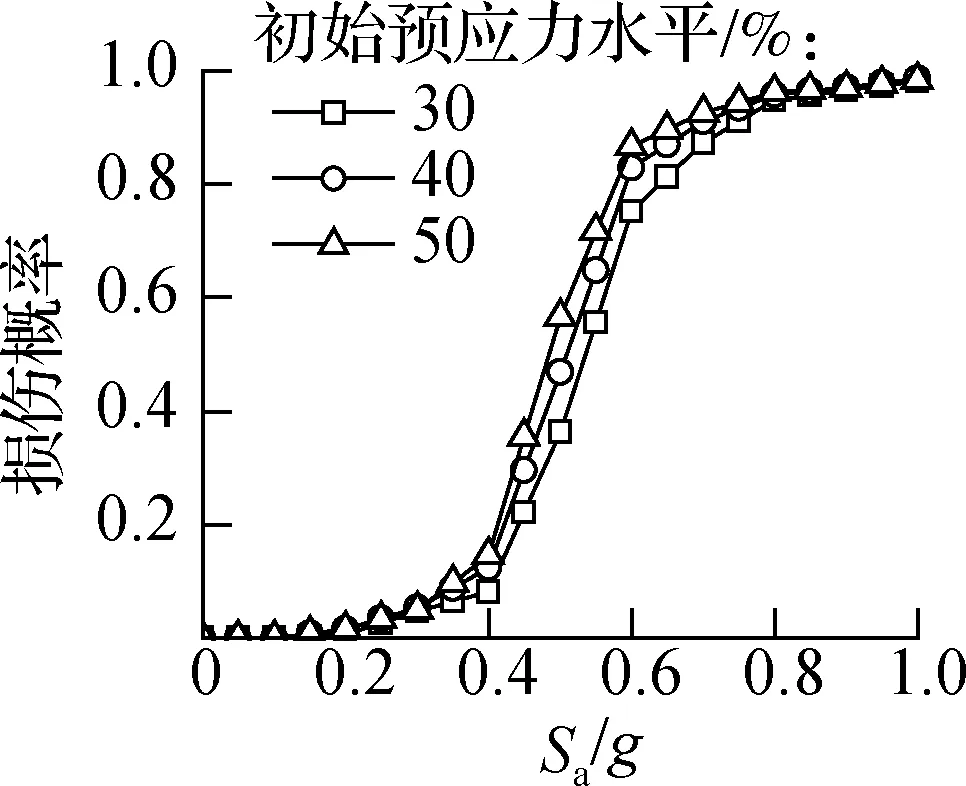
(c) 严重损伤
严重损伤和完全破坏状态下,随着预应力水平的提高,桥墩发生损伤的概率逐渐增大.当Sa=0.6g时,初始预应力水平为30%、40%、50%的桥墩发生严重损伤的超越概率分别为75.1%、82.3%、86.2%.这是因为相同轴压比条件下,提高初始预应力水平会导致桥墩延性性能降低.强震作用下,高应力状态的预应力筋可能发生屈服,导致桥墩的变形需求增大,桥墩发生严重损伤和完全破坏的概率也增大.
4.4 节段个数的影响
图12为不同节段个数的预制拼装桥墩和整体现浇桥墩(CIP)的易损性曲线.由图可知,各损伤状态下的超越概率均随Sa的增大而增大,相同损伤状态下,预制节段拼装的损伤概率均大于整体现浇桥墩.当Sa=0.5g时,预制拼装桥墩轻微损伤、中等损伤、严重损伤及完全破坏4种状态的超越概率分别为100%、100%、53.7%、2.3%,对应的整体现浇墩分别为89.6%、81.9%、25.7%、0%,说明相同地震作用下预制拼装桥墩更易受到损伤.对于节段个数不同的预制拼装桥墩,其易损性曲线在各级损伤水平下基本保持一致,节段个数对4种损伤概率的影响均较小.Li等[20]针对不同节段个数预制拼装桥墩开展了拟静力试验,结果表明,节段数目的改变未对桥墩滞回曲线、接缝张开宽度、骨架曲线等产生影响;这是因为桥墩墩身范围内各截面侧向刚度基本相同,加载过程中主要表现以受弯为主,仅有墩底接缝变形比较明显,其他位置接缝未见张开,因此节段数量并不影响桥墩整体性能.基于KDE法计算的易损性曲线与文献[20]的结论基本一致,说明在当前分析范围内,节段个数对桥墩地震损伤基本没有影响.
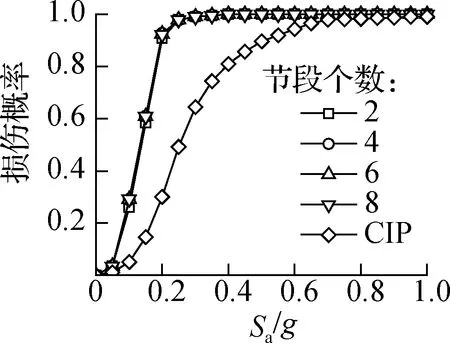
(a) 轻微损伤
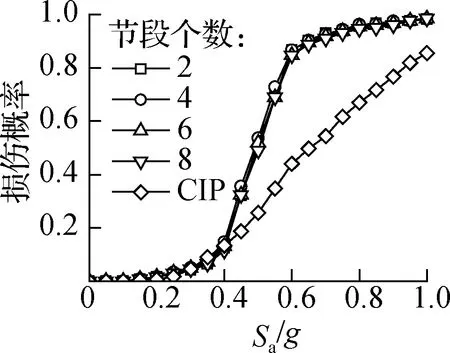
(c) 严重损伤
5 结论
1)预制拼装桥墩的IDA分析表明,提高混凝土强度等级和初始预应力水平会降低桥墩极限位移延性比,改变节段个数则对IDA曲线影响不明显.
2)在一定范围内提高混凝土强度可以降低预制拼装桥墩发生轻微、中等和严重损伤的概率,但当混凝土强度等级超过C50时,由于高强混凝土脆性特征比较明显,增加混凝土强度反而会使桥墩位移延性比降低.当Sa=0.9g时,混凝土强度等级为C30、C40、C45、C50的桥墩发生完全损伤的概率分别为64.7%、54.9%、49.0%、70.9%,说明提高混凝土强度增加了桥墩发生完全破坏的概率.
3)提高预应力筋的初始预应力水平会增加预制拼装桥墩发生严重损伤和完全破坏的概率.当Sa=0.6g时,初始预应力水平为30%、40%、50%的桥墩发生严重损伤的概率分别为75.1%、82.3%、86.2%.
4)相同地震作用下,预制拼装桥墩比同尺寸整体现浇墩更易受到损伤.当前参数讨论范围内,节段个数的变化对结构的损伤概率影响较小,但节段个数作为装配式桥墩关键参数,后续仍需进行深入研究.
