锆钛酸铅薄膜的铁电疲劳微观机理及其耐疲劳性增强*

王志青 姚晓萍 沈杰 周静† 陈文 吴智

1) (武汉理工大学材料科学与工程学院, 材料复合新技术国家重点实验室, 武汉 430070)

2) (浙江大学材料科学与工程学院, 杭州 310058)

3) (湖南工学院材料与化学工程学院, 衡阳 421002)

铁电随机存储器(ferroelectric random access memory, FeRAM)因其卓越的数据存储性能与非易失性存储特性等优势而备受关注, 但其自身固有的铁电疲劳失效问题制约了FeRAM进一步的发展和商业化应用.FeRAM的疲劳失效与铁电薄膜的畴壁运动密切相关, 但其内在疲劳机理仍有待深入研究. 本文采用基于密度泛函理论(density functional theory, DFT)的第一性原理计算方法, 研究了锆钛酸铅 (Pb(Zr0.52Ti0.48)O3,PZT) 的疲劳失效机理并提出了增强其耐疲劳性能的方法. 计算结果表明: PZT中氧空位与180°畴壁运动的耦合是其铁电疲劳的内在原因, PZT铁电薄膜中越靠近畴壁的地方越容易形成氧空位, 畴壁处大量氧空位对畴壁运动的“钉扎”作用使畴壁迁移困难, 抑制了其极化反转最终导致了铁电疲劳; Ba(Mg1/3Nb2/3)O3 (BMN)缓冲层的存在可吸收PZT中的氧空位, 降低畴壁处的氧空位浓度, 提升其耐疲劳性能. 实验结果表明, 经过1010次极化反转后, PZT 铁电薄膜的剩余极化值降低了51%, 而PZT/BMN薄膜的剩余极化值仅降低了18%;经过1012次极化反转后, PZT/BMN 薄膜的剩余极化值仍保持有82%并持续稳定. 以上结果表明, BMN缓冲层引入确实能提高PZT铁电薄膜的耐疲劳性, 有望满足FeRAM商业化应用的需求.

1 引 言

当代大数据的开发, 云计算、通信和电子产品的发展对信息存储器性能提出了更高的要求, 信息存储市场对非易失性存储器的需求量与日剧增. 相较于其它新型存储器, 铁电随机存储器(ferroelectric radom access memories, FeRAM)因其低功耗、快读写速度、高密度存储、抗辐射性能好和非易失性存储等优势受到研究人员的广泛关注[1-7]. FeRAM的核心为铁电薄膜材料, 在特定方向上可以发生极化翻转, 从而实现数据“0”和“1”的存储[8,9]. 然而, 铁电薄膜在多次极化翻转操作后,容易发生剩余极化下降、铁电性能退化的问题, 此即为“铁电疲劳”, 对此研究人员已经开展了大量的研究工作, 但至今仍存在疲劳失效机制不清和不能有效改善铁电薄膜耐疲劳性能等问题, 阻碍了FeRAM的进一步商业化发展[10,11].

目前, 铁电薄膜的疲劳失效机制主要存在以下三种: 畴壁钉扎机制(wall pinning mechanism)[12]、籽畴抑制机制(seed inhibition mechanism)[13]和局部疲劳机制(local imprint mechanism)[14]. 以上三种疲劳机制通常包括以下两个步骤: 一是缺陷的形成和重分布; 二是缺陷影响铁电薄膜的极化反转[15]. 这些疲劳机制都涉及缺陷及缺陷浓度的变化, 研究人员多采用氧空位模型[16]和电荷注入模型[17]来有效解释缺陷浓度变化: 在氧空位模型中,Dawber等[18]认为薄膜中本征氧空位会在外电场作用下迁移至界面处造成“籽畴”抑制或者畴壁“钉扎”, 最终导致铁电薄膜产生疲劳; 在电荷注入模型中, 交流电场下的电子和空穴会从金属电极注入到铁电薄膜中并在电极/铁电薄膜的界面处聚集产生低介电常数层进而削弱施加在铁电薄膜上的有效电场, 从而降低其极化强度, 最终导致铁电疲劳[19,20].

研究表明, 在铁电薄膜与电极之间引入具有中低介电常数的缓冲层作为一层电容界面层, 可有效阻止源自底电极的电荷注入[21,22]. 在课题组前期的研究中[23], 在铁电薄膜和金属电极界面处引入Ba(Mg1/3Ta2/3)O3(BMT)作为介电氧化物缓冲层, 有效改善了铁电薄膜的耐疲劳性. 相较于BMT介电层, Ba(Mg1/3Nb2/3)O3(BMN)具有中低介电常数、低介电损耗、小漏电流, 同时与铁电薄膜具有相似的晶体结构和高的晶胞填充率, 可作为界面介电氧化物缓冲层, 有望阻碍铁电薄膜与电极之间的相互扩散, 改善铁电薄膜的疲劳性能.

在微观层面, 铁电薄膜的耐疲劳性能与铁电薄膜中畴壁的物理性质及其动力学演化过程息息相关. 铁电材料中铁电畴的产生及其尺寸由边界条件决定, 同时畴的尺寸也决定了畴壁的密度. FeRAM会有反复的读写操作, 这就要求铁电薄膜在外电场下具有较高的极化反转次数, 归结到畴壁的动力学演化过程上, 就是要求畴壁可以在外场作用下实现迅速迁移. 研究人员采用粒子在力场中的运动方程来描述宏观上的铁电畴壁动力学, 认为畴壁运动受外加电场、有效势代表的内力、畴壁与声子和点缺陷相互作用所产生的摩擦力共同作用的影响[24].在大量实验的基础上, 研究人员明确了铁电极化反转的整个过程, 主要包括以下四个过程: 一是新畴成核; 二是畴的纵向长大; 三是畴的横向扩张; 四是畴的合并[25,26]. Zhi等[27]采用数字全息干涉技术, 获得了外电场作用下畴成核、生长和畴壁运动等过程的微观变化图. Shin等[28]采用蒙特卡罗算法从微观角度模拟了畴成核、生长和畴壁运动的具体过程, Gopalan等[29]研究了180°畴的动力学演化过程. 借助基于密度泛函理论(density functional theory, DFT)的第一性原理计算, 将薄膜中的多畴简化为超晶格的双畴, 可在原子尺度上对畴壁及其演化过程进行模拟, 反映畴壁运动的实质, 进而可在原子尺度上深入分析铁电薄膜的疲劳失效机理.

锆钛酸铅Pb(ZrxTi1—x)O3, (PZT)是铁电材料的典型代表, 其优异的铁电性能受到研究人员的广泛关注. 在PZT中, 当Zr/Ti比为52/48时, PZT结构中存在一条准同型相界(morphotropic phase boundary, MPB), 此时的PZT薄膜受到外加电场作用时, 内部的铁电活性离子更容易发生迁移和极化, 可以获得更优异的铁电性能. 因此, 本文将借助DFT计算模拟, 以典型的锆钛酸铅(Pb(Zr0.52Ti0.48)O3, PZT)铁电材料为例, 在原子尺度上模拟氧空位与畴壁之间的耦合作用, 深入研究PZT的疲劳微观机理; 在此基础上, 在PZT与金属电极界面处引入BMN介电氧化物作为界面缓冲层以提升铁电薄膜的耐疲劳性, 并分析BMN增强PZT耐疲劳性能的内在机理.

2 实验与理论计算

2.1 实验部分

2.1.1 PZT/BMN复合薄膜的制备

五氧化二铌(Nb2O5, 纯度 ≥ 99.0%)、氢氧化钾(KOH, 纯度 ≥ 99.0%)、柠檬酸(C6H8O7·H2O,纯度 ≥ 99.5%)、双氧水(H2O2, 纯度 ≥ 30.0%)、钛酸钡(BaCO3, 纯度 ≥ 99.0%)、三水合乙酸铅((Pb(OAc)2)·3H2O、乙酰丙酮(CH3COCH2COCH3,纯度 ≥ 99.0%)和乙二醇甲醚(HOCH2CH2OCH3,纯度 ≥ 99.5%)均购自中国国药化学试剂有限公司. 正丙醇锆(Zr(OCH2CH2CH3)4, 纯度70%)和异丙醇钛(Ti(OCH(CH3)2)4, 纯度 ≥ 98%)均购自上海阿拉丁生化科技股份有限公司, 碱式碳酸镁((Mg CO3)4·Mg(OH)2·5H2O, 纯度 ≥ 99.0%)购自上海泗联化工厂有限公司.

采用溶胶-凝胶法制备均一、稳定的淡黄色PZT前驱体溶液: 以HOCH2CH2OCH3为溶剂,Zr (OCH2CH2CH3)4和Ti(OCH(CH3)2)4以及(Pb(OAc)2)·3H2O为原料, CH3COCH2COCH3作为稳定剂. 采用水溶液凝胶法制备BMN前驱体溶液:以水作为溶剂, Nb2O5, KOH, C6H8O7·H2O, H2O2,BaCO3和(Mg CO3)4·Mg(OH)2·5H2O作 为 原 料,HO(CH2)2NH2作为稳定剂. 采用旋涂法制备PZT/BMN复合薄膜: 首先在基底上旋涂BMN, 并在180 ℃下加热2 min去除薄膜内的水分, 在380 ℃下加热2 min去除薄膜中的有机物; 然后放入快速退火炉中, 在600 ℃下预退火5 min; 最后放入马弗炉中, 700 ℃下退火1 h. 在BMN薄膜上继续旋涂PZT薄膜, 并在150 ℃下加热5 min去除薄膜内的水分, 在350 ℃下加热5 min去除薄膜中的有机物; 然后放入快速退火炉中, 在600 ℃下预退火5 min; 最后放入马弗炉中, 650 ℃下退火30 min.

2.1.2 PZT/BMN复合薄膜性能表征

X射线衍射(X-ray diffraction, XRD)分析采用荷兰PANalytical公司Pert-Pro型X射线衍射仪, 选用Cu-Kα辐射源, 测角精度 Δ 2θ≤±0.033°,扫描范围为2θ= 10°—80°, 扫描速率为10°/min.场发射扫描电镜(field emission scanning electron microcopy, FESEM)采用德国Zeiss公司Ultra Plus型场发射扫描电子显微镜. 薄膜铁电性能表征和疲劳性能测试采用美国Radiant公司的Precision Workstation铁电测试分析仪, 分别表征薄膜的铁电性能和疲劳性能.

2.2 理论计算

本文采用基于DFT的赝势平面波第一原理方法[22,30](VASP软件包), 利用缀加平面波赝势(project augmented wave, PAW)描述电子-离子之间的相互作用, 在PZT体系中, 局域密度近似(local density approximation, LDA)泛函会低估晶体的晶格常数, 而广义梯度近似(generalized gradient approximation, GGA)泛函能修正LDA的结果, 同时GGA中的PBEsol泛函在提高精度的同时可解决PBE泛函易高估四方PZT铁电性的问题. 因此, 计算时交换关联能采用GGA中的PBEsol泛函[31]. PZT为PTO和PZO的二元连续固溶体, 本文选用Zr/Ti比为1∶1的PZT晶胞进行建模和几何优化. 为了降低计算量, 在进行畴壁迁移和氧空位迁移的计算过程中, B位只采用一种钛元素来简化模型, 但所有输入数据遵循PZT的实际计算参数进行设置. 同时, 将薄膜中的多畴简化为超晶格的双畴, 在简化计算模型的同时, 还可以在原子层面上反映畴壁运动的实质, 辅助分析铁电疲劳的内在机理. 模型原子量适中(120个),可以在现有计算能力范围内实现模型的第一性原理计算.

2.2.1 结构优化

计算中交换关联能采用GGA中的PBEsol泛函[31], 平面波截断能(cut-off energy)设置为450 eV.计算中涉及的价电子分别是Pb: 5d106s26p2, Ti:3p63d24s2, O: 2s22p4. 考虑到GGA的近似处理方法在处理一些具有强关联作用的体系(过渡金属,如Ti元素等)时存在一定的缺陷, 故采用Hubbard模型[32]对GGA进行修正, 即GGA +U方法, 以更准确地描述体系的电子结构. 其中, 采用U=5 eV和J= 0.64 eV描述Ti原子的d轨道[33-35].采用Blòchl修正的四面体方法和9 × 9 × 9的Monkhorst-Packk点网络对倒空间进行积分; 采用共轭梯度方法(conjugate gradient method, CG)对原子进行弛豫, 直到每个原子所受的力(Hellmannfeynmann force)小于0.1 eV/nm.

2.2.2 畴壁能计算

构建超晶胞结构, 沿x(100)方向堆叠N×1 × 1个钙钛矿单胞(图1). 超晶胞中N/2个单胞自发极化方向向上(沿+z方向),N/2个单胞的自发极化方向向下(沿—z方向), 该超晶胞包含两种畴, 畴的厚度为N/2倍的晶格常数, DW(domain wall)表示180°畴壁, 超晶胞中共有2个畴壁. 畴壁能的计算公式如下[36]:

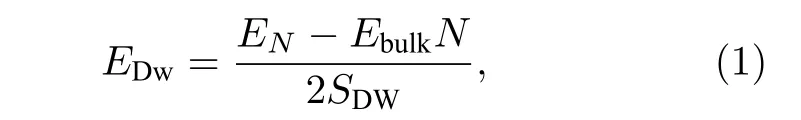
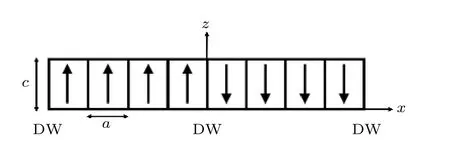
图1 包含8个钙钛矿单胞的超晶胞结构Fig. 1. Supercell structure containing 8 unit cells.

其中,EN是包含N个PTO钙钛矿单胞的超晶胞的能量,Ebulk是一个PZT单胞的能量,SDW是180°畴壁的横截面积, 公式中的2表示超晶胞中共有2个畴壁.

2.2.3 NEB方法模拟畴壁迁移

极化反转在微观上反映为畴壁的迁移, 微动弹性带(nudged elastic band, NEB)方法可以有效反映畴壁在两个平衡位置之间的动态运动. 采用NEB方法计算畴壁迁移的具体运动过程, 寻找畴壁迁移过程中的最小能量路径(minimum energy path, MEP)以及此路径上的过渡状态(transition Sstate, TS)和发生反应所需要的活化能(activation energy), 其具体计算过程如图2所示, 构建8 × 1 × 1的超晶胞模型, 包含一个可以迁移的畴壁和一个固定的畴壁. 初始态结构是由4个自发极化方向向上的单胞和4个自发极化方向向下的单胞构成的超晶胞, 终止态结构是由3个自发极化方向向上的单胞和5个自发极化方向向下的单胞构成的超晶胞, 初始态和终止态之间采用线性插值的方法构建了8个中间相.

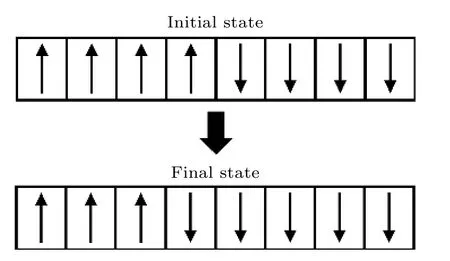
图2 NEB方法计算畴壁迁移中的初始态和终止态Fig. 2. NEB method to calculate initial state and ending state in domain wall migration.

2.2.4 畴壁对氧空位形成能的影响

采用8 × 1 × 3个单胞构成的超晶胞来计算畴壁对氧空位形成能的影响, 其中在x方向上一半的单胞自发极化方向向上, 另一半的单胞自发极化方向向下, 以位于中心不可移动的Pb-O-Pb链为畴壁. 钙钛矿结构的PZT中共有3种不同位置的氧离子: 沿x轴方向的氧离子O1, 沿y轴方向的氧离子O2和沿z轴方向的氧离子O3, 这3种氧离子对应产生3种不同的氧空位, 分别记为OV1, OV2和OV3. 在该模型中, 只考虑氧空位与畴壁之间的耦合作用, 不考虑氧空位之间的耦合作用, 并以氧空位与畴壁之间的距离为变量, 研究这一距离对氧空位形成能的影响. 氧空位形成能的计算公式如下:

其中,Ef是氧空位的形成能,Eperfect是完美体系结构弛豫后的总能量,Edefect是包含一个氧空位的体系结构弛豫后的总能量,u是单个氧离子的能量.

2.2.5 氧空位对畴壁迁移的影响

钙钛矿结构的PZT铁电极化主要沿z方向的钛氧相对位移产生[37], 该方向钛氧链上的氧空位OV3即是PZT中一种最重要的氧空位, 因此只需考虑OV3对畴壁迁移的影响. 采用由7 × 1 × 3个单胞构成的超晶胞来计算氧空位对畴壁迁移的影响, 其中OV3位于最中间的单胞的钛氧链上. 180°畴壁迁移的整个过程为由远离氧空位的位置到经过氧空位再到远离氧空位位置, 子过程即为180°畴壁从第n— 1个PZT晶胞和第n个PZT晶胞之间(初始态)迁移到第n个PZT晶胞和第n+ 1个PZT晶胞之间(终止态),n的范围为n∈[2, 6]且n为N*. 对每个子过程采用NEB计算方法, 由线性插值方法在每个子过程的初始态和终止态之间建立8个中间相结构.

2.2.6 PZT/BMN结构优化

采用缀加平面波赝势描述电子-离子之间的相互作用, 平面波截断能设置为450 eV, 交换关联能采用PBEsol泛函. 计算中涉及的价电子分别是Pb: 5d106s26p2, Zr: 4p64d25s2, Ti: 3p63d24s2, O:2s22p4, Ba: 5s25p66s2, Mg: 2s2, Nb: 4s24p64d35s2.采用U= 5 eV和J= 0.64 eV描述Ti原子的d轨道, 采用U= 6.8 eV描述Nb的d轨道. 固定底部的3层晶面(7个原子), 以此近似模拟无限大的衬底并构建20 Å的真空层以消除[001]晶面方向上由周期性边界条件而产生的人为伪电场. 采用偶极修正来消除偶极矩之间的相互作用, 并利用Blochl修正的四面体方法和9 × 9 × 1的Monk horst-Packk点网络对倒空间进行积分. 采用共轭梯度方法对原子进行弛豫, 收敛阈值为0.2 eV/nm.

3 结果与讨论

3.1 PZT耐疲劳性能增强

在Si/SiO2/Ti/Pt衬底上成功制备了PZT/BMN复合薄膜, 其结构示意图如图3(a)所示. 图3(b)—图3(d)分别为PZT薄膜、BMN薄膜和PZT/BMN复合薄膜的XRD图谱. 从图3可以看出, 薄膜均已结晶, PZT薄膜和BMN薄膜的XRD图谱分别与标准PDF卡片ICDD#17-0173和ICDD#73-2022相对应, 表明结晶状态良好的PZT薄膜和BMN薄膜得以成功制备. 由PZT/BMN复合薄膜的XRD图谱可以看出, 复合薄膜仍为典型的钙钛矿结构, BMN缓冲层的引入未破坏PZT的晶体结构且其特征衍射峰得到了明显增强, 这是由于BMN与PZT薄膜均为钙钛矿结构且衍射峰峰位非常接近, BMN缓冲层的引入相当于给PZT薄膜提供了一层促进其生长的籽晶层, 有利于提升PZT薄膜的结晶质量.

图3 (a) PZT/BMN薄膜的结构示意图; (b) PZT, (c) BMN和(d) PZT/BMN薄膜的XRD图谱Fig. 3. (a) Schematic of PZT/BMN films; XRD patterns of (b) PZT, (c) BMN, and (d) PZT BMN films.

PZT/BMN复合薄膜的表面和断面FESEM图像如图4所示. 图4(a), (b)所示分别为无BMN薄膜和BMN薄膜厚度为10 nm时上层PZT薄膜的表面扫描图像, 图4(c), (d)分别对应于图4(a), (b)的断面扫描图像, 可见引入BMN缓冲层后薄膜与基底的界面结合得到了明显增强. 插图所示为表面PZT薄膜的AFM图像, 引入BMN缓冲层后,PZT表面均方根(root mean square, RMS)粗糙度从4.04 nm降低为2.3 nm, 由FESEM图像和AFM图像可以看出, BMN缓冲层的引入可有效提升PZT薄膜的生长质量.

图4 (a)无BMN缓冲层和(b)有BMN缓冲层的PZT薄膜表面; (c)无BMN缓冲层和(d)有BMN缓冲层的薄膜断面FESEM图像Fig. 4. FESEM images of the surface PZT films (a) without or (b) with BMN buffer layer; cross-section of films (c) without or (d) with BMN buffer layer.

图5 (a)所示为PZT和PZT/BMN薄膜的电滞回线. 从图5(a)可以看出, 与不引入BMN缓冲层的PZT薄膜剩余极化强度 (Pr= 43.78 μC/cm2)相比,PZT/BMN复合薄膜的Pr增强至60.85 μC/cm2,同时电场和极化轴的不对称性加剧. BMN界面层的引入促进了PZT薄膜的生长, 提高了其结晶质量, 有利于PZT/BMN复合薄膜铁电性能的提高,同时BMN缓冲层的引入加剧了上下电极-薄膜界面的不对称性, 导致了在电场和极化轴不对称性的加剧.

图5 PZT薄膜和PZT/BMN薄膜的 (a)电滞回线和(b)疲劳性能Fig. 5. (a) Hysteresis loop and (b) fatigue failure of PZT and PZT/BMN films.

图5 (b)所示为PZT和PZT/BMN复合薄膜的极化疲劳特性曲线, 其中P*代表可翻转极化, 包括剩余极化部分和非剩余极化部分;代表不可翻转极化, 仅包括非剩余极化部分. 我们最感兴趣的是P*与P^的差值, 即剩余极化部分. 从图5(b)中可以看出, 随极化反转次数不断增加, PZT薄膜的剩余极化值Pr在循环107周期后迅速降低; 当极化反转周期为l010时, PZT薄膜的剩余极化值降低了51%. 在PZT薄膜与Pt电极之间引入BMN缓冲层后, 当极化反转周期为l010时, PZT/BMN复合薄膜的剩余极化值仅降低了18%, 并且当极化反转1012次时, PZT/BMN复合薄膜的剩余极化值仍保持稳定, 依旧保持有82%. 这一极化疲劳性能有望满足FRAM应用的需求.

3.2 PZT疲劳机理理论计算

在四方相PZT晶体结构中, 在Pb-O面O原子相对于Pb原子在z方向上发生位移; 在Ti(Zr)-O面Ti原子相对于O原子在z方向下发生位移.晶体结构、能带结构图和分波态密度(partial density of states, PDOS)图如图6所示, 单胞体积为65.56 Å3, 能带结构显示PZT禁带宽度为1.867 eV,与文献[38,39]计算得到的PZT禁带宽度保持一致.

图6 四方相的PZT (a)晶体结构; (b)能带结构图和PDOS图Fig. 6. (a) Crystal structures; (b) band structure and PDOS of tetragonal PZT.

3.2.1 180°畴壁迁移

超晶胞中畴壁运动过程中的能量变化与畴壁迁移的最小能量路径如图7所示. 其中, 畸变程度为0%和100%分别对应畴壁迁移过程中的初始态(顺电相)和终止态(铁电相). 初始态和终止态之间对应的8个点分别对应8个中间相结构. 畴壁迁移的能量势垒由鞍点和初始态(终止态)之间的能量差值决定, 其中初始态到鞍点的能量势垒是84.6 meV, 势垒能量密度是5.3 mJ/m2, 终止态到鞍点的能量势垒是83.0 meV, 势垒能量密度是5.2 mJ/m2. 具有不同单胞数目的超晶胞畴壁能计算结果如表1所示, 可见所有超晶胞的畴壁能均在110.0 m J/m2左右, 表明超晶胞中单胞的数目对180°畴壁能和畴结构的稳定性具有较小影响.

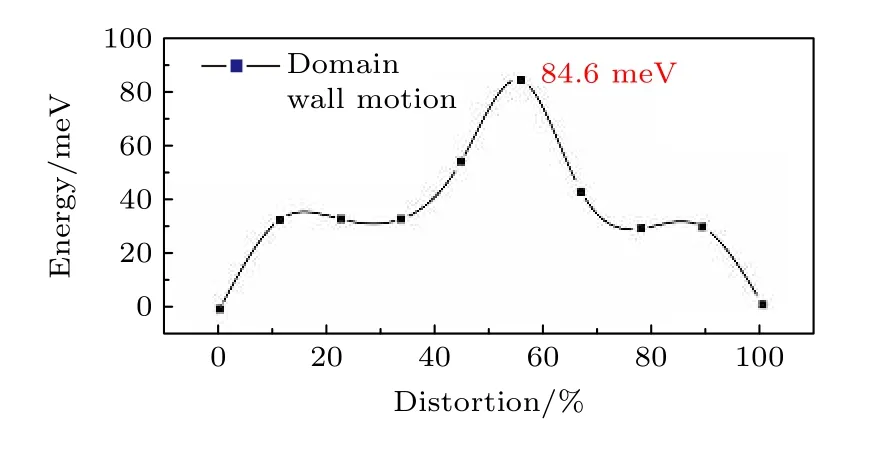
图7 PZT畴壁运动过程中的能量变化图Fig. 7. Diagram of energy changes during PZT domain wall motion.

表1 具有不同PZT单胞数目的体系的畴壁能Table 1. Domain wall energy of systems with different numbers of PZT unit cells.

3.2.2 氧空位和180°畴壁的耦合

不同类型的氧空位形成能随畴壁与氧空位之间的距离变化如图8所示, 可以看出: 氧空位OV1形成能最高, 说明沿x轴方向的氧空位最不容易形成; 氧空位OV2和OV3形成能较低, 说明沿y轴和z轴方向的氧空位比较容易形成. 另外, 随着氧空位与畴壁之间距离的缩小, 所有类型的氧空位形成能均降低, 尤其是OV1与畴壁重合时, 氧空位形成能最低. 以上结果说明, 畴壁可显著影响氧空位的形成, 越靠近畴壁的地方越容易形成氧空位, 畴壁处最容易形成氧空位.

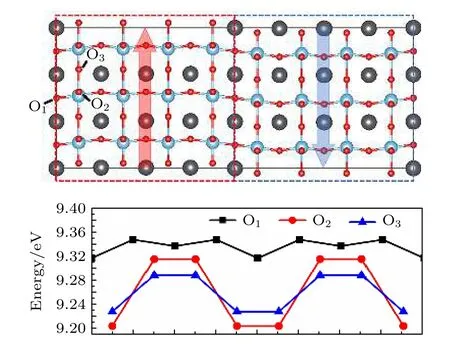
图8 PZT中不同类型氧空位的能量随畴壁与氧空位之间的距离变化图Fig. 8. The energy variations of different types of oxygen vacancies in PZT with the distance between the domain wall and the oxygen vacancies.

氧空位存在时超晶胞中发生畴壁迁移所需的能量变化如图9所示, 其中能量势垒的高低直接反映畴壁迁移的难易程度, 能量势垒越高畴壁迁移越困难, 可见氧空位的存在对畴壁迁移具有一定的影响: 在引入氧空位后, 畴壁迁移势垒从原来的84.6 meV增加到250.0 meV左右, 表明氧空位的存在导致畴壁迁移势垒增大, 畴壁迁移困难, 这直接反映了氧空位对畴壁的“钉扎”作用; 此外在畴壁迁移过程中的能量变化按氧空位所在位置呈左右对称分布, 在远离氧空位处畴壁迁移的能量势垒非常大(～0.25 eV), 随着畴壁与氧空位距离的下降, 畴壁迁移的能量势垒降低, 尤其是在经过氧空位的子过程中, 畴壁迁移的能量势垒最低(约为0.14 eV).

图9 氧空位下PZT中畴壁迁移过程中的能量变化图Fig. 9. Energy change diagram during the migration of domain walls in PZT with oxygen vacancies.

从计算结果同样可以看出, 畴壁在向靠近氧空位迁移的过程中超晶胞能量不断降低, 体系越来越稳定; 畴壁在向远离氧空位迁移的过程中超晶胞能量不断升高, 体系越来越不稳定. 当畴壁迁移到氧空位处时即落入由氧空位形成的势阱, 从而导致畴壁的可动性大大降低, 这就是氧空位对畴壁的“钉扎”作用, 一旦畴壁被氧空位形成的势阱所困, 体系需要外界提供很高的能量“去钉扎”, 才能够保证畴壁迁移(也就是极化反转)的顺利进行, 这即从微观角度解释了氧空位对畴壁的“钉扎”作用. 而氧空位对畴壁的“钉扎”作用也是导致铁电薄膜产生疲劳的根本原因之一[12], 在氧空位的作用下, 畴壁因在氧空位形成的势阱处发生“钉扎”而迁移困难, 导致极化反转被抑制, 最终导致铁电薄膜产生疲劳.

3.3 BMN增强PZT耐疲劳性能机理

氧空位在PZT/BMN界面迁移过程中的能量变化如图10所示, 可以看出, 氧空位从PZT迁移到BMN的能垒值为0.601 eV, 从BMN迁移到PZT的能垒值为1.293 eV, 即从热力学角度说明了位于BMN层中的氧空位比位于PZT层中的结构更稳定. 图11给出了引入BMN缓冲层后PZT耐疲劳性能增强的机理示意图. 在不引入BMN的初始状态时, 如图11(a)所示, 薄膜制备过程中产生的氧空位随机分布在PZT薄膜中, 此时氧空位的存在并未对PZT的极化反转产生影响. 随着PZT极化反转次数增加, 如图11(b)所示, 由于畴壁在越向靠近氧空位的位置处体系越稳定, 在电场作用下氧空位会逐渐迁移至畴壁处, 并对畴壁进行“钉扎”, 致使PZT的极化反转被抑制, PZT薄膜产生疲劳.

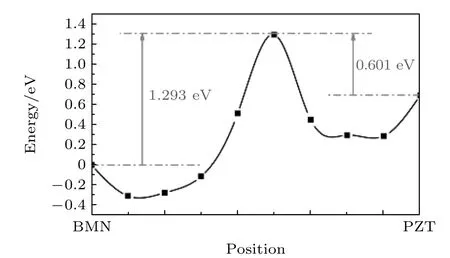
图10 氧空位在PZT/BMN界面迁移过程中的能量变化图Fig. 10. Energy change diagram of oxygen vacancies during the migration process at PZT/BMN interface.

由于氧空位迁移到BMN层中具有更低的能垒(0.601 eV), 引入BMN缓冲层以后, 能量壁垒的不同导致氧空位可以很容易迁移进入到BMN缓冲层内部, 因此BMN层可以很好地吸收PZT中的氧空位. 当在PZT与衬底之间引入BMN后,如图11(c)所示, 氧空位逐渐从PZT层迁移进入BMN层中并稳定存在. 如图11(d)所示, 大量的氧空位迁移至BMN缓冲层中, PZT中留下了少量的氧空位, PZT薄膜中氧空位浓度的减少降低了氧空位对畴壁运动的“钉扎”作用, PZT耐疲劳性能得以增强.

图11 体系耐疲劳性增强的机理图 (a), (c)引入BMN缓冲层前后的体系初始状态; (b), (d) 引入BMN缓冲层前后的体系发生严重疲劳后的状态 (图中圆点表示氧空位)Fig. 11. The mechanism diagram of system fatigue resistance enhancement: (a), (c) The initial state of the system before and after the introduction of the BMN buffer layer; (b), (d) the state of the system before and after the introduction of the BMN buffer layer after severe fatigue (The dots in the figure indicate oxygen vacancies).

4 结 论

本文以BMN薄膜作为缓冲层来增强PZT薄膜的铁电耐疲劳性能, 分析了PZT薄膜的疲劳机理和耐疲劳增强机理. 实验结果表明, PZT铁电薄膜在经过1010次极化反转后的剩余极化值降低了51%, 在引入BMN缓冲层后, PZT/BMN叠层薄膜在经过1012次极化反转后的剩余极化值仍持有82%并保持稳定. 第一性原理计算表明, 氧空位与180°畴壁运动的耦合是PZT薄膜铁电疲劳的内在原因, BMN缓冲层的引入可有效降低PZT薄膜中的氧空位浓度, 消除由于氧空位“钉扎”作用而导致的PZT薄膜的铁电疲劳问题, 从而增强了PZT薄膜铁电疲劳性能. 以上结果表明, BMN缓冲层引入确实能提高PZT铁电薄膜的耐疲劳性, 有望满足FeRAM商业化应用的需求.