甚低频台站信号对地球内辐射带和槽区能量电子的散射效应分析*

2021-08-05刘阳希子项正郭建广顾旭东付松周若贤花漫朱琪易娟倪彬彬3

物理学报 2021年14期

刘阳希子项正† 郭建广顾旭东付松周若贤花漫朱琪易娟倪彬彬3)

1) (武汉大学电子信息学院, 武汉 430072)

2) (中国气象局国家空间天气监测预警中心, 北京 100081)

3) (中国科学院比较行星学卓越创新中心, 合肥 230026)

人工地面甚低频台站发射的10—30 kHz信号主要在地球—低电离层波导传播, 部分能量会泄露进入内磁层, 进而会影响近地空间中高能电子的动态变化过程. 本文详细研究了NWC, NAA和DHO38三个人工甚低频台站信号对内辐射带和槽区高能电子的散射作用. 基于准线性理论, 分别计算了三个甚低频台站信号单独和共同作用时对高能电子的弹跳平均投掷角扩散系数, 并进一步利用Fokker-Planck扩散方程模拟内辐射带及槽区的高能电子在200 d内的动态演化过程. 结果表明, 在低L-shell (L ≤ 1.8), NWC台站信号对电子的损失占主导作用, 可以使能量在100 keV附近、投掷角小于60°的电子出现明显损失; 在较高的L-shell(2.2 ≤ L ≤ 2.7), 主要是NAA和DHO38台站信号占主导作用, 可以使能量小于20 keV、投掷角小于70°的电子通量显著下降; 三个甚低频台站信号对高投掷角(＞ 80°)的电子均无显著影响.

1 引言

地球辐射带是近地空间环境的重要组成部分,存在于辐射带中的高能电子和高能质子会对运行其中的卫星、载人航天设备和宇航员构成巨大威胁, 因此研究辐射带的动态变化同时具有重要的科学意义和应用价值. 按照空间区域划分, 地球辐射带可分为内带、槽区和外带.

通常认为外辐射带的变化较为剧烈[1-3]而内辐射带相对稳定. 近期的研究结果表明, 内辐射带的高能电子会在磁暴期间因为注入而增强, 然后在平静时期逐渐下降[4,5]. 宇宙射线反照中子衰变[6-9]、自然激发的哨声波(如等离子体层嘶声[10,11]、雷电产生的哨声波[12-14]等)、磁声波[15-17]以及地面台站发射的甚低频(very low frequency, VLF)信号[18-20]都能对内辐射带及槽区的高能电子通量产生影响. 其中, 地面人工台站发射的10—30 kHz的VLF信号主要用于对潜通信, 可以在地球-低电离层波导中进行远距离的传播, 通过地面VLF接收机[21,22]接收的VLF信号, 可用于反演电离层的变化特征[23-25]. VLF信号在沿地球-低电离层波导传播时, 会有小部分穿透电离层, 泄露进入内磁层,与电子发生回旋共振, 使其扩散进入损失锥, 从而沉降到大气中[26-33]. 近几十年来, 国内外的专家学者在地面人工台站VLF信号影响辐射带电子动态变化这一方向做了很多研究. 如直接观测到了与台站发射波形ON/OFF调制周期一致的粒子沉降周期[34-36]; 通过DEMETER卫星的观测数据[37,38]和射线追踪模拟[39], 得出了NWC台站发射的信号会引起内磁层中大于100 keV电子沉降的结论;通过准线性理论定量计算了VLF信号在与辐射带电子发生回旋共振时, 改变不同的参数对投掷角扩散系数大小的影响[40,41]. 这些研究大多基于理论计算和射线追踪得到VLF台站信号的波模, 并没有使用实际观测结果. 通过范艾伦探测双星中的A星的数据, 文献[18]得到了10—60 kHz的VLF台站信号在磁层中的统计模型, 并计算了VLF台站信号与嘶声共同散射时, 内辐射带及槽区的电子的生命周期将下降1—2个数量级; 文献[42]统计了VLF台站信号在磁层中的全球分布. 文献[19]根据文献[42]的结果计算了VLF台站信号、嘶声和库仑碰撞联合散射时对高能电子的散射效应, 结果表明VLF台站信号可以使内磁层中500 keV电子的生命周期, 在200 d内下降一个数量级, 使槽区40 keV电子的生命周期在100 d内下降一个数量级.

在分析VLF台站信号对高能电子的散射效应时, 之前的研究大多使用投掷角扩散系数来计算电子损失时间尺度[18,33], 这一方法的优点是步骤简单、计算量小, 缺点是无法具体分析不同投掷角电子在损失时的详细演化过程. 为了系统、细致分析各个VLF台站信号对不同投掷角高能电子的散射效应, 本文在文献[42]统计模型基础上, 使用准线性理论计算NWC, NAA和DHO38三个台站发射的VLF信号对高能电子的弹跳平均投掷角扩散系数, 并将其代入到一维Fokker-Planck方程求解高能电子在全投掷角范围的演化过程. 第2节介绍使用的理论模型, 第3节介绍模拟结果, 第4节总结.

2 理论模型

2.1 投掷角扩散率的计算

统计结果[42]表明, 在内辐射带和槽区中, 50%以上的VLF台站信号能量来自于NWC, NAA,DHO38这三个台站, 因此本文主要分析这三个台

站的VLF信号对内辐射带和槽区高能电子的散射效应. 之前的研究表明, 在L＜ 1.7, VLF波主要以非导管的方式传播(在赤道附近, 波的传播方向与磁力线之间夹角约为60°—70°); 而在更高的Lshell, VLF波主要以导管的方式传播(即波沿磁力线近似于准平行传播)[18,29,38,39]. 根据这些结论, 本文假设在L＜ 1.7的VLF台站信号全部为非导管传播; 在1.7 ≤L＜ 2.5的VLF台站信号, 25%的波是非导管传播, 75%为导管传播; 在L≥ 2.5的VLF台站信号为导管传播[18]. 本文使用文献[42]对VLF台站信号的统计结果作为内辐射带和槽区VLF台站信号分布的主要依据. 因为文献[42]在计算VLF台站信号的波幅时假设在所有的Lshell, 波均以导管的方式传播(即波传播角θ= 0°),本文首先采用文献[43]的等离子体层密度模型和偶极子磁场模型, 将文献[42]中VLF台站信号的磁场功率谱密度转换为电场功率谱密度[44]. 然后再假设非导管波的传播角为θ= 65°, 导管波的传播角为θ= 0°[18], 将VLF台站信号的电场功率谱密度转换为对应的磁场功率谱密度[44]. 最后使用新的磁场功率谱密度计算VLF台站信号的波幅,这样计算的结果使用了VLF台站信号在空间中的实际传播特性, 与实际情况更加接近. 三个VLF台站信号的波幅随L-shell的分布关系如图1所示.这三个VLF台站的发射频率、功率、地理位置、及L-shell分布范围如表1所列.

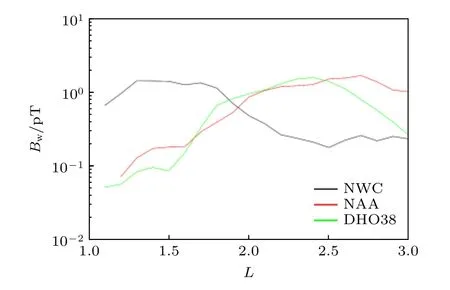
图1 计算得到的三个台站的波幅Fig. 1. Calculated wave amplitudes from three VLF transmitters.

根据上面计算的VLF台站信号波幅, 使用FDC程序[45](full diffusion code)计算了VLF台站信号引起的电子弹跳平均投掷角扩散系数〈Dαα〉 ,在计算投掷角扩散系数时考虑的共振阶数为|N| ≤10. VLF台站信号的频谱分布采用高斯分布, 中心频率为各台站的发射频率(见表1), 半波带宽为δw=100Hz. 传播角的模型也采用高斯模型, 对于导管传播的VLF台站信号, 具体传播角的模型参数选取为θm=θmin=0°,θmax=30°,θw=10°[18];对于非导管传播, 传播角的模型选取为θm=65°,θmin=45°,θmax=80°,θw=10°[18]. 由于高斜波的传播角需要满足θ≤min(θmax,θr) (resonance cone angle:θr=arccos(f/fce) ), 于是设定折射指数的范围为n＜ 200[46], 超过这个范围后, 将投掷角扩散系数Dαα置为0. VLF台站信号的纬度覆盖范围, 对于导管传播为 ≤ 45°, 对于非导管传播为≤ 25°[18,32,39].

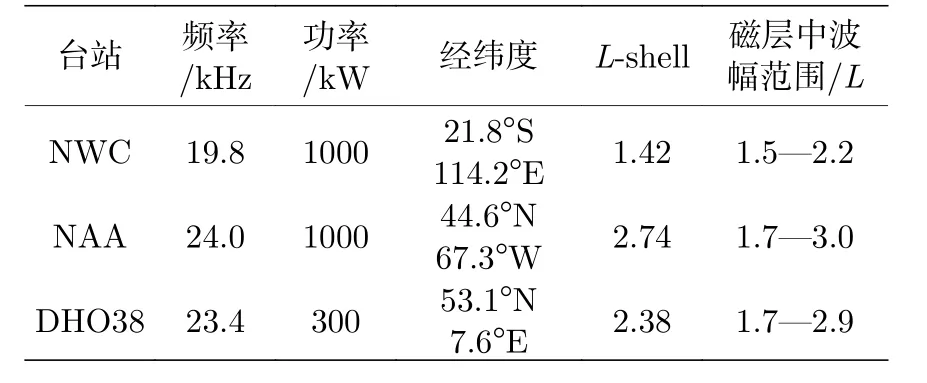
表1 选取计算的台站信息Table 1. The information of the three selected VLF transmitters.

2.2 一维Fokker-Planck扩散方程

为了详细分析VLF台站信号对不同投掷角电子的散射效应, 本文将计算得到的弹跳平均投掷角扩散系数应用于求解一维Fokker-Planck扩散方程[47], 模拟电子相空间密度(phase space density,PSD)的演化过程. 一维Fokker-Planck扩散方程为

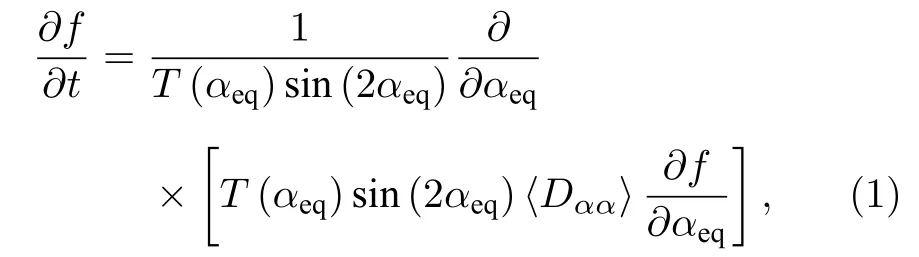
其中αeq为电子的赤道投掷角,T(αeq)≈1.30-0.56sinαeq,f表示电子的PSD. 为了方便计算, 初始电子PSD采用Kappa分布[15,48], 表达式为

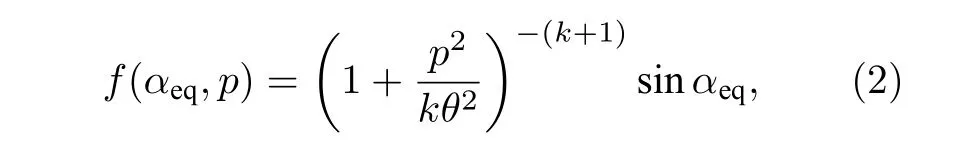
其中k= 6.0, 为Kappa指数;θ2=0.15 ,θ是归一化的热速度,p是电子动量. 对于投掷角的边界条件, 将损失锥内(αeq≤αL, 其中sinαL=L-3/2(4-3/L)-1/4)的f置为0, 在αeq=90°时设置∂f/∂αeq=0. 对于能量的边界条件, 当Ek=1keV和Ek=1MeV 时, 设置f为固定值.

3 结果分析

3.1 扩散系数计算结果

图2为NWC台站信号在L= 1.5—2.2引起的弹跳平均电子投掷角扩散系数. 图中横坐标为电子的赤道投掷角, 纵坐标为电子能量, 颜色表示电子投掷角扩散系数的大小. 以L= 1.5为例, 扩散系数分为两部分, 其中一部分集中在能量为400—1000 keV, 投掷角为0—57°的范围, 是电子与VLF信号发生回旋共振导致的. 可以发现, 随着能量的增加, 发生回旋共振的投掷角范围也在增加, 而扩散系数峰值在最小共振能量处, 最小共振能量随着投掷角的增加而增大. 另一部分投掷角扩散系数是电子与VLF台站信号发生朗道共振导致的. 相对于回旋共振, 朗道共振导致的扩散系数要弱1—2个数量级. 在L= 1.6—2.2, 投掷角扩散系数的分布特征与L= 1.5的相似, 最小回旋共振能量随着L-shell的增加而降低, 这是因为电子回旋频率随着L-shell的增加而降低[18,19]. 在L= 1.6和L= 1.7的波幅相近, 但L= 1.7处回旋共振(低投掷角)的扩散系数明显增大, 而朗道共振(高投掷角)的扩散系数相对减弱, 这是由于在L=1.7处导管传播的VLF台站信号比例(75%)高于L= 1.6 (0%), 这些结果说明当波幅相近时, 导管传播的VLF台站信号对电子的散射效应要明显强于非导管传播的VLF台站信号. 在L= 1.7和L= 1.8处, 投掷角扩散系数最大, 约为 1 0-8s-1, 而在L≥ 1.9时, 因为VLF台站信号的波幅随L-shell的增加而减弱, 投掷角扩散系数也相应地随L-shell的增加而减弱.

NAA台站信号和DHO38台站信号引起的电子弹跳平均投掷角扩散系数如图3和图4所示. 图的格式与图2相同, 投掷角扩散系数的特征也与图2相似. 由于NAA和DHO38这两个台站的发射频率相近, 在相同的L-shell, 两个台站信号散射的电子能级范围和投掷角范围几乎一致, 随着Lshell的增加, NAA和DHO38台站信号能散射更小能量的电子, 如在L= 2.6处, 扩散系数的峰值在几keV. 随着投掷角的增加, 扩散系数的峰值移向更高能量的电子. 在更高的L-shell, 扩散系数的峰值下移至几百eV能量. 由图1可以看出, NAA和DHO38台站的波幅在L= 2.2—2.7较大, 这些L-shell相应的的扩散系数也较大, 最大值可达到约 1 0-7s-1. 对比图1中两个台站信号的幅值,可以看出在L= 1.7— 2.4处, DHO38台站信号的幅值较大, 相应的DHO38台站信号引起的投掷角扩散系数更大; 而在L= 2.6—2.9处, NAA台站信号幅值更大, 相应的投掷角扩散系数更大. 比较三个台站的扩散系数可以发现, 在相同的L-shell,最小共振能量随着台站频率的增加而减小, 而投掷角扩散系数的大小, 主要由波幅的大小决定.

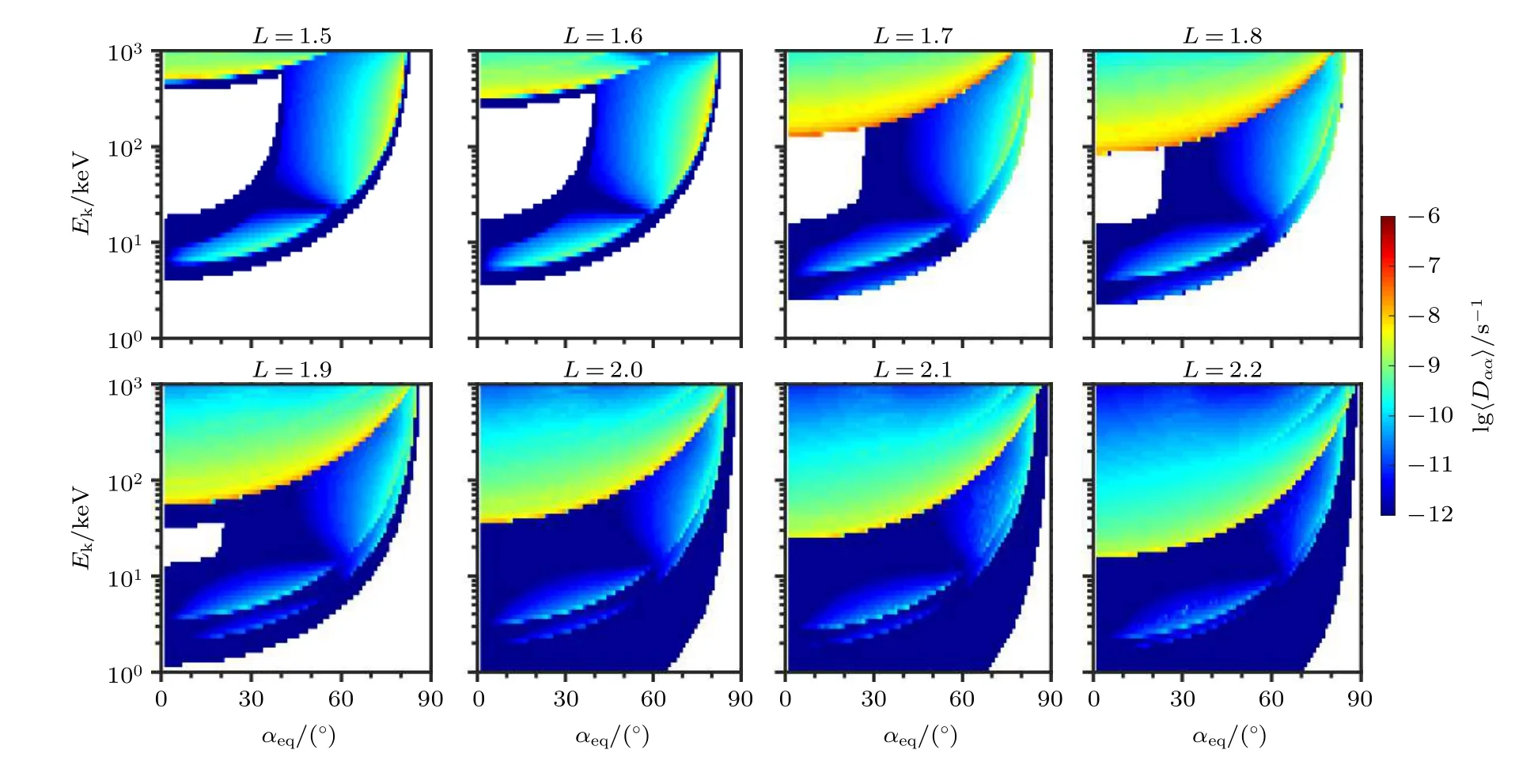
图2 NWC台站信号在L = 1.5—2.2导致的电子弹跳平均投掷角扩散系数〈 Dαα〉. 图中横坐标为赤道投掷角 α eq , 纵坐标为电子能量 E k , 颜色表示扩散系数的大小Fig. 2. The color-code bounce-averaged pitch angle diffusion coefficients 〈 Dαα〉 as a function of equatorial pitch angle α eq and electron kinetic energy E k induced by VLF transmitter signals from NWC at L = 1.5—2.2.

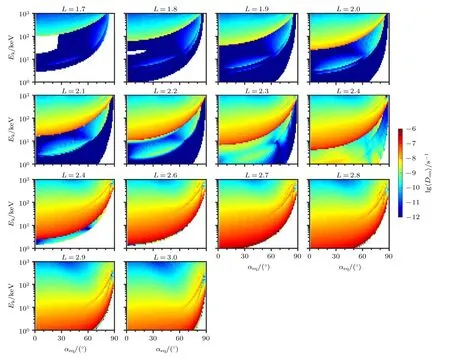
图3 NAA台站信号在L = 1.7—3.0导致的电子弹跳平均投掷角扩散系数. 格式同图2Fig. 3. Same as in Fig. 2 except for VLF transmitter signals from NAA at L = 1.7—3.0.

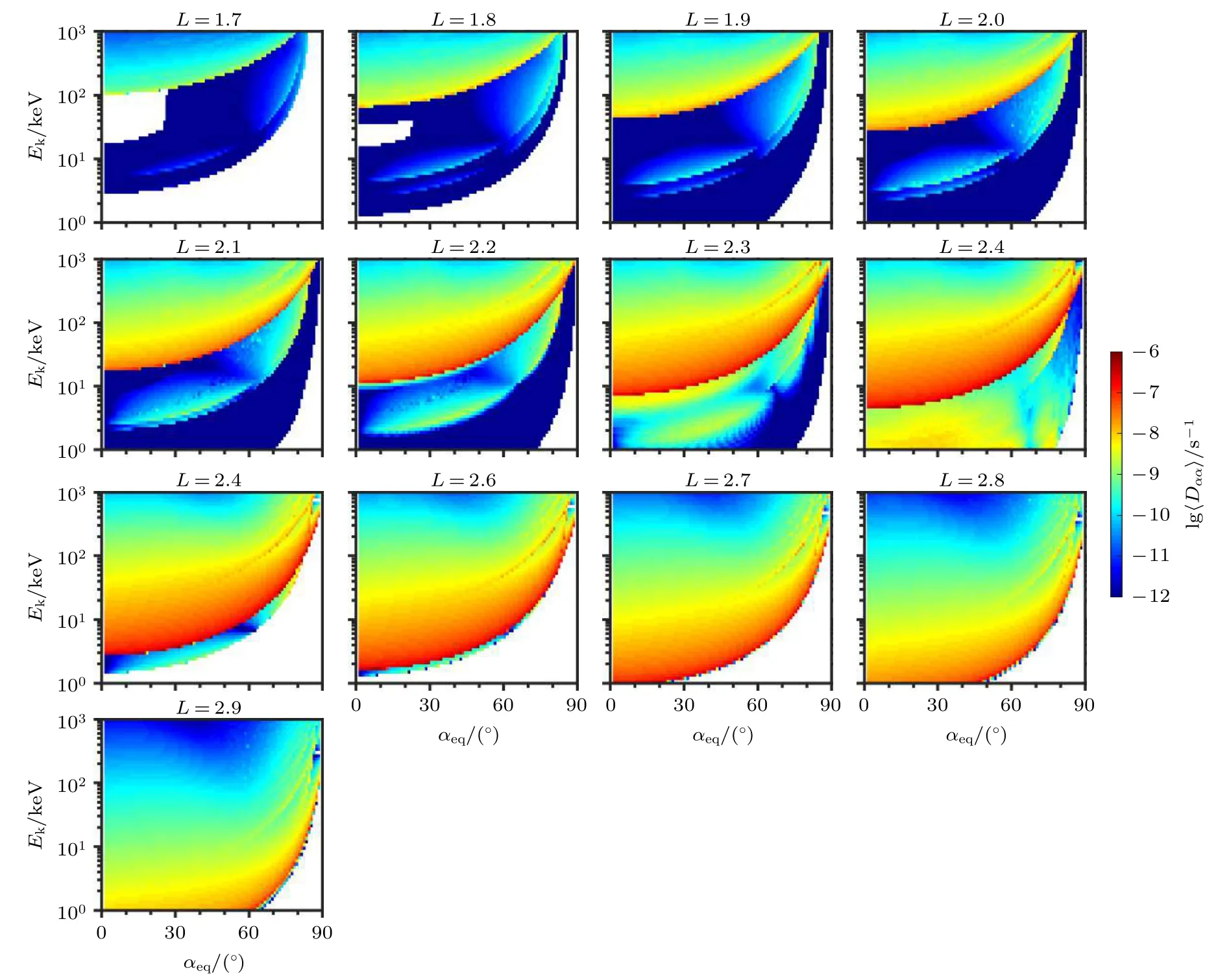
图4 DHO38台站信号在L = 1.7-2.9导致的电子弹跳平均投掷角扩散系数. 格式同图2Fig. 4. Same as in figure 2 except for VLF transmitter signals from DHO38 at L = 1.7-2.9.

3.2 散射效应模拟结果

为了进一步研究VLF台站信号对内辐射带和槽区不同投掷角高能电子的散射效应, 计算VLF台站信号导致的电子弹跳平均投掷角扩散系数后,将其用于求解一维Fokker-Planck扩散方程.

图5是L= 1.8处, 在VLF台站信号的作用下, 电子PSD随时间演化过程的模拟结果.初始的电子PSD投掷角分布如图5(a1)所示,图5(b1)—图5(d4)为采用不同VLF台站信号(从左至右分别为NWC, NAA, DHO38台站单独作用和三个台站信号的联合作用), 高能电子PSD演化的分布图(从上至下分别为50, 100和200 d).图中横坐标为电子赤道投掷角, 纵坐标为电子能量, 颜色表示电子PSD的大小. 图中空白区域为损失锥(电子赤道投掷角小于20°的范围). 从图5可以看出, 在L= 1.8处, NWC台站信号对电子的散射作用最强, 可以使90—120 keV、赤道投掷角小于40°的电子PSD在200 d内减少至少一个数量级; NAA和DHO38台站信号只对80 keV左右、损失锥附近的电子有散射作用. 这与上一节计算的投掷角扩散系数分布是对应的. 三个VLF台站信号联合散射时, 电子PSD下降范围与NWC台站信号单独作用时大体一致. 表明在低L-shell,NWC台站信号对高能电子的散射起主导作用.

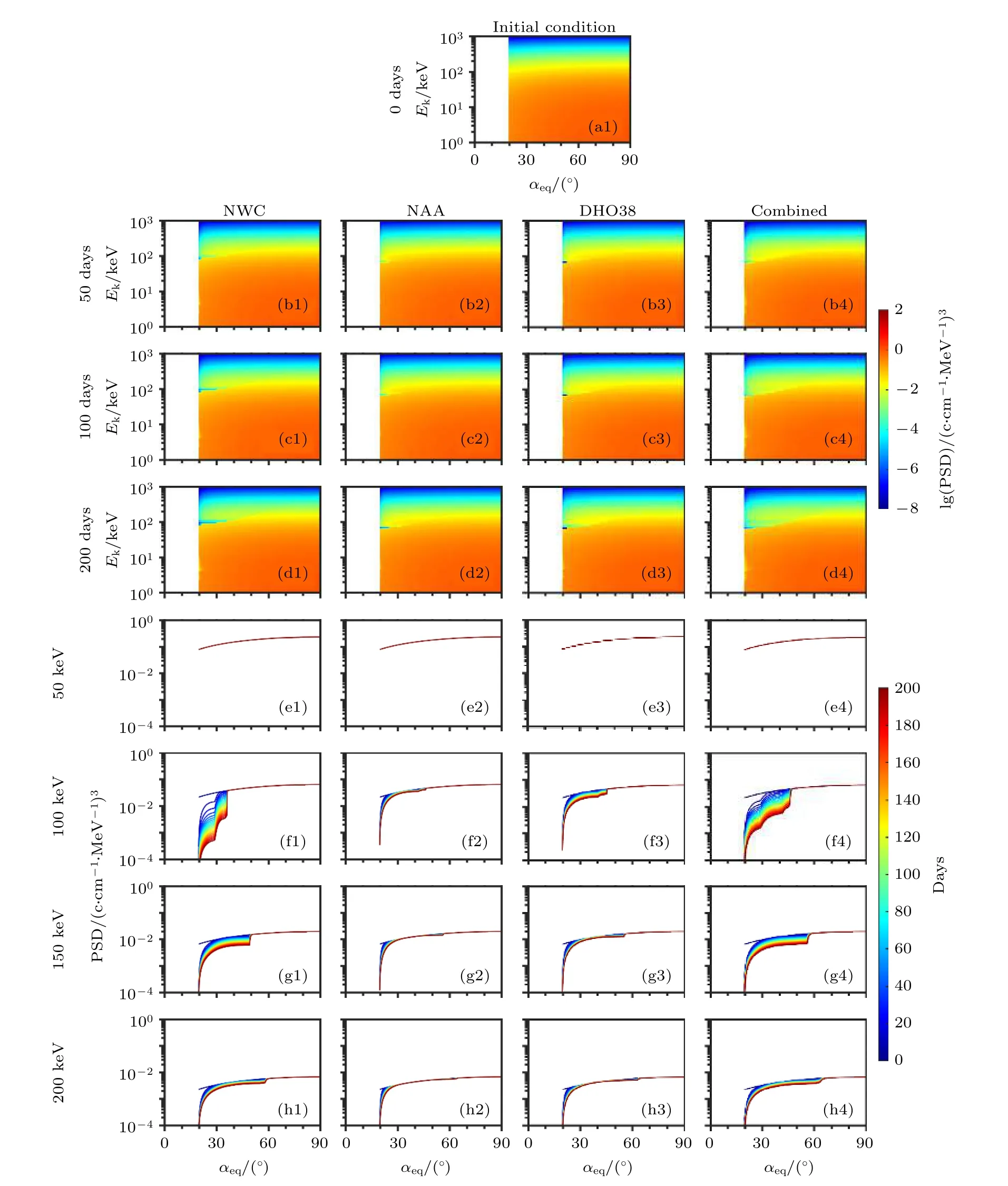
图5 在L = 1.8处, 不同VLF台站信号对电子散射效果的模拟, 从左至右分别为NWC, NAA, DHO38台站信号单独散射和三个台站信号联合散射 (a1)-(d4)不同模拟时间的电子相空间密度分布二维图, 颜色表示电子相空间密度的大小; (e1)-(h4)指定能级电子的相空间密度随时间演化的过程图, 线条颜色表示不同的时间Fig. 5. (a1)-(d4) Two dimensional distributions of color-code electron phase space density (PSD) as a function of equatorial pitch angle α eq and electron kinetic energy E k at the indicated interaction time stamps at L = 1.8 induced by different VLF transmit ter signals (from left to right): NWC, NAA, DHO38 individual scattering and combined scattering; (e1)-(h4) temporal evolution of electron PSD distribution as a function of α eq for the indicated four electron energies at the color-coded interaction time stamps.

图5(e1)—图5(h4)给出了在不同VLF台站信号的作用下, 指定能级电子PSD随时间的演化.图中横坐标是电子赤道投掷角, 纵坐标是电子PSD, 线条颜色代表不同时间. 可以看出, 对于100 keV电子, NWC台站信号可以使低投掷角(＜ 40°)电子PSD在200 d内减少一个数量级左

右, 并且电子越接近损失锥, 损失效果越明显. 但NAA和DHO38台站信号对电子无明显散射效应.所有VLF台站信号对于高投掷角(＜ 80°)电子均无明显散射效应.

在L= 2.2和L= 2.6处, VLF台站信号作用下, 电子PSD随时间演化的模拟结果如图6和图7所示, 图的格式与图5相同. 对比不同L的模拟结果可以发现, 发生损失的电子能量随L-shell的增加而减小. 在L= 2.2 (图6)处, NWC台站信号只对约 20 keV电子有微弱的散射作用, 而NAA台站信号和DHO38台站信号对电子的散射作用较强, 主要散射10—20 keV、投掷角小于50°的电子,且DHO38台站信号对电子的散射作用更强. 如NAA台站信号可以使20 keV、投掷角小于50°的电子PSD在200 d内减少5倍, DHO38台站信号能使之减少一个数量级. 在L= 2.6(图7)处, NAA,DHO38台站信号对几keV、投掷角小于60°的电子有较强的散射作用, NAA台站信号的散射作用更强. 如DHO38台站信号能使5 keV、投掷角小于60°的电子PSD在200 d内减少5倍,而NAA台站信号能使之减少一个数量级. 当这两个VLF台站的信号联合散射时, 电子损失加快.由图6和图7可以看出, 在2.2 ≤L≤ 2.7, 主要是NAA和DHO38台站的信号引起电子的损失,且电子损失的速度与VLF台站信号幅值的大小成正比.