一维双方势垒量子隧穿的研究及其数值模拟
2022-01-13李海凤王欣茂
李海凤, 王欣茂
(西安工业大学 基础学院物理系,陕西 西安 710021)
量子隧穿(或量子贯穿、量子隧道)是一种重要的量子效应,当入射粒子能量小于势垒高度,其仍然有一定的概率穿过势垒,出现在势垒后面的区域.而当入射粒子能量略微高于势垒高度,仍然有一定概率在势垒表面发生反射.这些现象用经典力学无法解释,必须借助于量子力学理论,其本质为微观粒子具有波粒二象性[1-4].因此,量子隧穿现象是粒子具有波动性的表现.利用量子隧穿效应,能够非常好地解释放射性元素α衰变、热核聚变、金属电子冷发射、半导体p-n结、隧道二极管等.除此之外,量子隧穿效应的重要实际应用之一为扫描隧道显微镜,1993年利用扫描隧道显微镜制成了量子围栏,人类首次直接观测到电子驻波图.
传统量子物理教材,只涉及单个方势垒,势垒范围一般是x∈(0,a),然后计算微观粒子的透射系数,若一维任意边界的双方势垒,中间形成一个量子阱,如何计算微观粒子的透射系数?不同于散射矩阵方法(或转移矩阵方法),本文利用量子力学求解势垒量子隧穿的常规方法,严格分区域求解定态薛定谔方程,并且利用波函数在边界处满足单值性和连续性,推导得到一维任意边界条件下双方势垒量子隧穿透射系数的精确解析表达式,虽然推导过程比较繁琐,但是结果简洁,能够比较直观得出透射系数与哪些参数有关.这些都是非常有意思的问题,不仅可以作为量子力学学习和教学的补充,并且可以对纳米电子器件的设计和制造提供物理依据[5-10].
1 非对称双方势垒
一维任意边界的非对称双方势垒,两个垒宽与两个垒高均不等.势能函数如下:
(1)

图1 一维非对称双方势垒
从图1中可知两个垒高分别为U01和U02, 两个垒宽分别为L1=b-a,L2=d-c, 两个势垒之间的间距为Δ=c-b.第Ⅰ、Ⅲ、Ⅳ区域一般为超导体、导体、金属,半导体材料等,电子可以自由运动,势能为零,而Ⅱ、Ⅳ区域一般为绝缘层,电子不容易通过,将其看成势垒.
由于势能函数不显含时间,双方势垒将空间分成五个区域,求解每个区域的定态薛定谔方程,得到每个区域的波函数形式解如下:
(2)
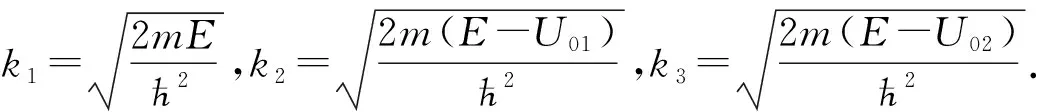
在每个区域的边界处,利用波函数标准条件(即单值性与连续性),求得
(3)

(4)

(5)
上述公式,给出了一维非对称双方势垒,3种不同入射能量情况下,F/A表达式,透射系数是它的模平方,虽然我们这里没有展示透射系数的具体表达式,但是从目前的结果比较容易看出透射系数是势垒宽度(L1,L2)、垒间距(Δ)、入射能量和垒高(E,U01,U02)的函数.下面我们重点通过研究一维对称双方势垒,数值模拟透射系数对上述参数的依赖关系.
2 对称双方势垒
一维对称双方势垒,垒高相同,即U01=U02=U0.
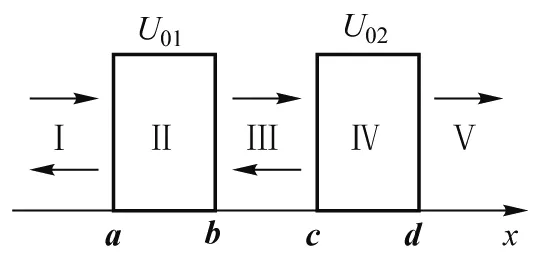
图2 一维对称双方势垒
那么它的势能函数U(x)为
(6)

(7)
对上式求模平方,则透射系数为
T=4β4/{(β2-1)4sin2(k1Δ)sin2(k2L1)sin2(k2L2)-
2β(β2-1)2sin(k2L1)sin(k2L2)sin(k1Δ)×
{2βcos[k2(L1+L2)]sin(k1Δ)+
(β2+1)sin[k2(L1+L2)]cos(k1Δ)}+
β2(1+β2)2sin2[k2(L1+L2)]+
4β4cos2[k2(L1+L2)]}
(8)

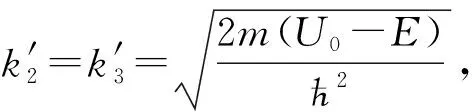
(9)
对上式求模平方,则透射系数为
T=4β′4/{β′2(β′2-1)2sinh2[k′2(L1+L2)]+
(β′2+1)4sinh2(k′2L1)sinh2(k′2L2)sin2(k1Δ)-
2(β′2+1)2sin(k1Δ)sinh(k′2L1)sinh(k′2L2)×
[(β′3-β′)cos(k1Δ)sinh[k′2(L1+L2)]+
2β′2cosh[k′2(L1+L2)]sin(k1Δ)]+
4β′4cosh2[k′2(L1+L2)]}
(10)
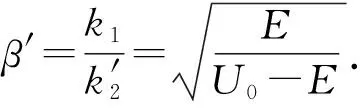
若Δ=0,L1=0或者L2=0.则一维双方势垒的结果回归到单方势垒的结果.
3 数值计算与讨论
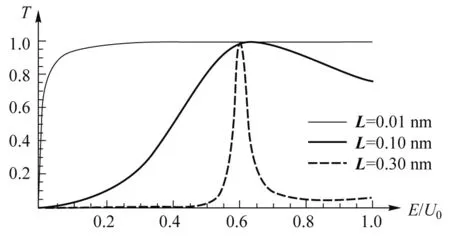
现在我们考虑一维对称双方势垒,两个垒宽相等,即L1=L2=L,并且微观粒子入射能量小于垒高的情况,即E T=4β′4/{β′2(β′2-1)2sinh2(2k′2L)+ (β′2+1)4sinh4(k′2L)sin2(k1Δ)+ 4β′4cosh2(2k′2L)- 2(β′2+1)2sin(k1Δ)sinh2(k′2L)· [(β′3-β′)cos(k1Δ)sinh(2k′2L)+ 2β′2cosh(2k′2L)sin(k1Δ)]} (11) 图3为一维对称双方势垒的透射系数与势垒宽度变化关系图,其中入射粒子能量为E=2 eV,势垒高度为U0=3 eV,势垒间距为Δ=0.2nm.当势垒宽度为0时,相当于没有势垒,粒子自由运动,透射系数为1,随着势垒宽度逐渐增加,透射系数逐渐减小,直至为0.从图中看出,若垒宽比较小(Δ≤0.11nm),双方势垒透射系数持续保持为最大值1, 说明垒宽越小越容易实现量子隧穿效应. 图3 一维对称双方势垒的透射系数与垒宽关系 图4为一维对称双方势垒的透射系数与势垒间距变化关系图,其中入射粒子能量为E=2eV,势垒高度为U0=3eV,势垒宽度为L=0.1nm.若势垒间距为0,相当于单方势垒,透射系数小于1,随着势垒间距逐渐增加,透射系数增加至1,然后又降低,呈现明显地周期式振荡,振动周期相同.若势垒高度变大,透射系数仍然随着势垒间距的增加而周期振荡,只不过透射系数最小值变小,峰宽变窄,更局域. 图4 一维对称双方势垒的透射系数与垒间距关系 为了便于理解,令透射系数取最大值1,我们解析地推导出此时垒间距表达式如下: (12) 将两个势垒之间区域看作一个量子阱,若势阱宽度(即两个势垒之间的距离)等于式(12),进入势阱的微观粒子在势阱界面上经历多次反射,微观粒子透射波保持相位的相干性,就可能具有接近于1的透射系数,使隧穿具有共振特性.因此,一维对称双方势垒的透射系数对于势垒间距具有明显的依赖关系.我们可以通过调控势垒间距,使微观粒子透射系数达到最大值1,进而实现共振隧穿. 图5为一维对称双方势垒在不同势垒宽度情况下透射系数随着E/U0变化的关系图,其中势垒高度为U0=3eV,双势垒间距为Δ=0.2nm.当入射粒子能量为0时,透射系数为0.当垒宽较大时(L=0.3nm),随着入射能量的增加,透射系数从零先增加到最大值然后急速减少,降到略大于0的某个值,然后趋于平缓.当垒宽处于中间值区域时(L=0.1nm),随着入射能量的增加,透射系数从零先增加到最大值1,然后缓慢减少.当垒宽较小时(L=0.01nm),随着入射能量的增加,透射系数从零首先快速增加到最大值1,然后稳定保持该值.从图中,我们比较容易看出,当垒宽比较大时,一般情况而言,量子隧穿效应不明显,透射系数比较低,甚至为0,但是可以通过选择合适的微观粒子入射能量,使透射系数达到最大值1.势垒宽度越大,透射系数对入射能量的选择依赖性越强. 图5 一维对称双方势垒不同垒宽下透射系数与E/U0 图6为一维对称双方势垒不同垒间距下透射系数与E/U0变化的关系图,其中势垒高度为U0=3eV,势垒宽度为L=0.1nm.微观粒子的入射能量为0时,透射系数为0.当双势垒间距较小时(Δ=0.2nm),随着入射能量的增加,透射系数从0缓慢增加到1,然后缓慢减小.当双势垒间距介于中间值时(Δ=0.4nm),随着入射能量的增加,透射系数从0增加到1然后缓慢减少至某个值后又缓慢增加.当双势垒间距(Δ=2nm)较大时,随着入射能量的增加,透射系数从0快速增加到1,然后快速减小,周期振荡,周期越来越大,但振幅越来越小.从图中可以看出,势垒间距越大越容易实现共振隧穿现象,由于当粒子入射能量等于两垒之间势阱区域的共振能级时,粒子可以利用共振隧穿的方式通过对称双方势垒. 图6 一维对称双方势垒不同垒间距下透射系数与E/U0 量子隧穿效应,虽然是根据微观粒子的波动性,贯穿比自身能量更高势垒的量子理论,但是它在实际技术中具有重要应用.本文利用量子力学求解定态薛定谔方程的常规方法,严格推导了一般任意边界条件下,一维双方势垒的透射系数,并且数值研究了对称双方势垒的透射系数与垒宽、垒间距以及入射能量与垒高比值的变化关系.在这些影响一维双方势垒透射系数的参数中,垒间距给出的结果比较有趣, 即透射系数随着垒间距的增加而呈现出明显地周期式振荡.本文我们首次推导得出透射系数达到最大值1时对应的垒间距解析表达式,从中比较容易得到振荡的周期,通过微观粒子的德布罗意波长关系,进一步证明了该振荡周期正好等于粒子的物质波波长.除此之外,透射系数随着垒宽的增加而缓慢从1减小至0.透射系数并不是随着入射能量的增加而单调递增至1,这种美好图景只有在垒宽比较小时才可以实现,对于垒宽稍微大或者较大时,只有当入射能量达到某一个值时,才会出现透射系数为1的峰值,然后随着入射能量继续增加,透射系数逐渐降低.当垒间距较小时,入射能量等于某个值时才会出现透射系数为1的峰,而当垒间距较大时,随着入射能量的增加,透射系数周期越来越大,振幅越来越小地振荡前进,实现共振隧穿. 因此,通过选择合适的入射粒子能量和势垒间距,可以极大地增加微观粒子通过势垒的透射系数.本文对于电子器件、共振隧穿器件的制作与研发以及解释半导体异质结构中共振隧穿现象具有指导意义,提供了物理理论依据.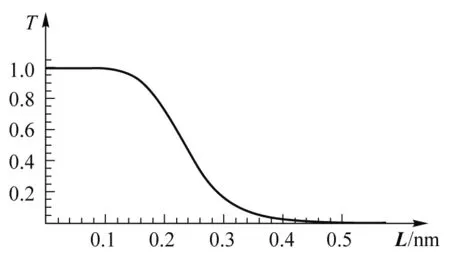



4 结论
