基于多阶段贝叶斯网络法的脐带缆全寿命周期可靠性分析

张 洲，夏 冉，郑利军，马国印，张 玉

(1. 中国石油大学(北京) 安全与海洋工程学院，北京 102200；2. 中海油研究总院，北京 100027；3. 海洋石油工程股份有限公司，天津 300450)

作为水下生产系统的关键组成部分，脐带缆是连接水上终端和水下生产系统之间的“神经生命线”。在海洋环境工作过程中，脐带缆从上部设施向水下设备传输液压油、化学药剂和电力，并在它们之间传递控制信号及温度、压力等数据[1]。

由于脐带缆(图1)自身重量等功能载荷以及波浪、海流、浮体运动等环境载荷的作用，脐带缆在储存、安装及在位运行期间会受到不同的损伤，为脐带缆的安全运行带来了不确定性[2]。例如，在储存阶段，放在卷筒或转盘上的脐带缆受到弯曲载荷和挤压载荷，由于转盘半径有限或脐带缆承重过大会造成弯曲失效和挤压失效[3]；安装过程中，铺管船将脐带缆慢慢铺设到海底，当安装船发生偏转时，在脐带缆的触底点容易发生扭转失效；在位运行阶段，脐带缆在复杂载荷作用下容易发生疲劳失效、拉伸失效和弯曲失效等[4]。

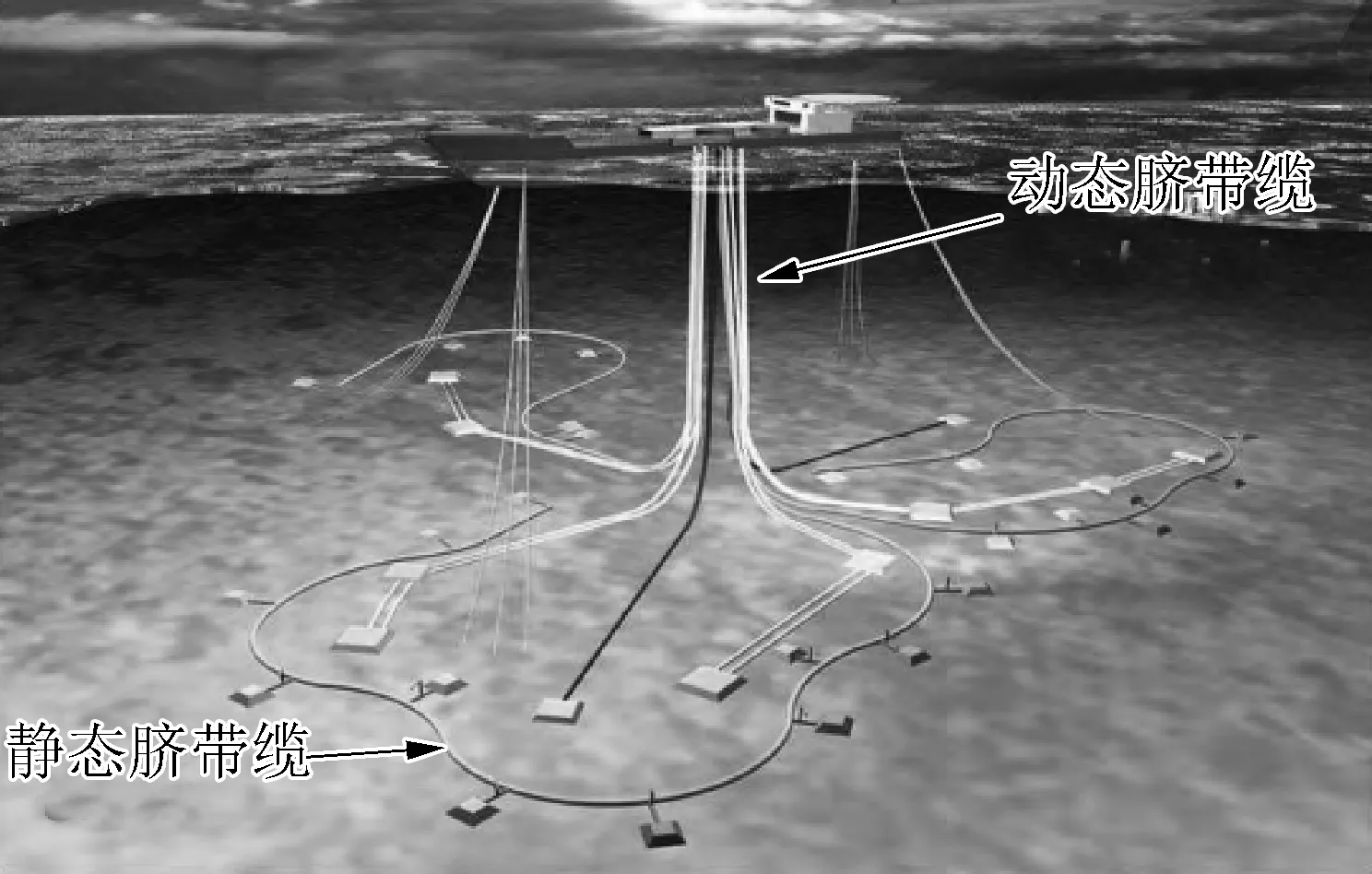
图1 水下生产系统中的脐带缆Fig. 1 The umbilical in subsea production system

脐带缆的可靠性对整个水下生产系统的安全运行起着关键的作用，一些学者对脐带缆的可靠性进行了相关的研究。Ventikos等[5]在大数据模型基础上建立了水下电缆可靠性分析模型，对自然和人为因素诱导的失效进行评估，从而选择最佳的铺设路线。Lee等[6]通过RAM研究定性与定量分析了海底生产系统的整体可靠性，以评估其可用性与可维护性，但并未就脐带缆进行具体分析。许文虎等[7]利用故障树分析方法，以南海某油气田水下生产系统脐带缆为研究目标，对其可靠性进行了定性、定量分析；阎军等[8]在考虑脐带缆结构不确定性的情况下，利用改进的一次二阶矩和蒙特卡洛法对脐带缆危险截面进行了强度可靠性分析。Joao等[9]通过使用系统可靠性框图(RBD)的方法，分析了脐带缆在位运行期间的可靠度随时间变化曲线，以对脐带缆寿命延长工作提出建议。但是，目前的研究对脐带缆在存储、安装、运行、修复等多阶段全寿命周期的可靠性研究比较少。在多阶段系统可靠性分析方面，刘东等[10-11]对多阶段贝叶斯网络(PMS-BN)进行了研究，并以反导系统为例进行可靠度分析计算，但其系统模型较为简单且失效原因单一；Tang等[12-13]基于二叉决策图(BDD)对考虑共因失效、多模式失效的多阶段系统(PMS)进行了可靠性分析。

文章提出基于多阶段贝叶斯网络分析脐带缆全寿命周期可靠性的方法。首先建立脐带缆在储存、安装、在位运行阶段的故障树模型，并将其转化为多阶段贝叶斯网络模型进行可靠性分析，依据OREDA数据库[14]对脐带缆全寿命周期可靠度进行了计算。然后将多阶段贝叶斯网络分析结果与RBD方法分析结果进行了对比，并分析了脐带缆关键部件重要度随时间的变化，识别脐带缆的薄弱环节并给出改进措施。最后通过引入条件可靠性对多阶段贝叶斯网络方法进行了优化，并分析了脐带修复后的可靠性。

1 脐带缆全寿命周期可靠性分析

脐带缆系统全寿命周期由设计制造、储存、安装、在位运行、修复阶段等五个不同的阶段组成，在时间上具有连续性和不重叠性的特征，系统在每个阶段的配置、正常工作的要求和部件的工作状态都会随着阶段的不同而变化。从系统可靠性的角度出发，脐带缆系统可视为多阶段系统(PMS)。在PMS中，不仅多个部件在同一阶段内存在相关性，而且同一部件在不同阶段之间也存在相关性，这也就造成了PMS可靠性分析的困难。

目前对PMS可靠性分析的常用方法主要为以下几种。第一，割集法是一种组合模型，具有简单、直观等特点[15]。但仍然具有组合爆炸的隐患，对于脐带缆这种复杂系统并不适合。第二，二叉决策图(BDD)是一种快速求解静态PMS可靠性的机制[16]。通过求解PMS-BDD可以得到PMS的可靠性，由故障树转化为BDD图，获得系统的所有故障模式和传播途径。但其本质上是一种静态的逻辑代数分析方法, 难以描述系统的动态行为(如系统单元为可修)。第三，马尔可夫链模型是可靠性工程中有效的建模工具[17]。其优点是能够正确描述阶段内各部件之间的依赖性以及部件跨阶段的依赖性，但需要构造复杂的微分方程，求解容易出错。第四，可靠性框图(RBD)是研究系统与部件之间的逻辑图，通过图形来表达系统单元与其可靠性之间的关系，能描述单元的正常或失效状态对系统状态的影响[18]。但它只能反映各个部件之间的串并联关系，无法描述部件顺序的影响。第五，多阶段贝叶斯网络法(PMS-BN)具有简单直观的特点，该方法首先建立系统每个阶段的BN模型，然后再据此建立整个PMS的BN模型[10]。

脐带缆不仅在不同阶段有着不同的可靠性，而且构造与失效原因复杂。其构成通常包括各类钢管、电缆等数十种部件，且部件与部件之间的可靠性会相互影响。例如，若钢管破裂，其内部具有腐蚀性的液体流出会影响电缆、光纤等部件的正常运行；若动力电缆电流过载产生高温，又会降低钢管、铠装层等材料的拉伸性能。所以对于脐带缆这种具有时间阶段性、构造复杂性以及部件单元之间相互影响的系统，在分析其可靠性时应该考虑到这些因素，选择合适的方法。PMS-BN具有BN特有的推理机制，不但可以分析脐带缆系统在不同阶段的可靠性，而且可以描述部件之间的影响，故相比其他PMS方法具有更高的准确性，并且可进行系统的故障诊断、重要度分析和寿命预测等更复杂的应用。由于PMS-BN的诸多特点适用于脐带缆系统全寿命周期内的可靠性评估，故采用基于多阶段贝叶斯网络法对脐带缆系统进行全寿命周期可靠性分析。

1.1 脐带缆多阶段贝叶斯网络可靠性分析模型

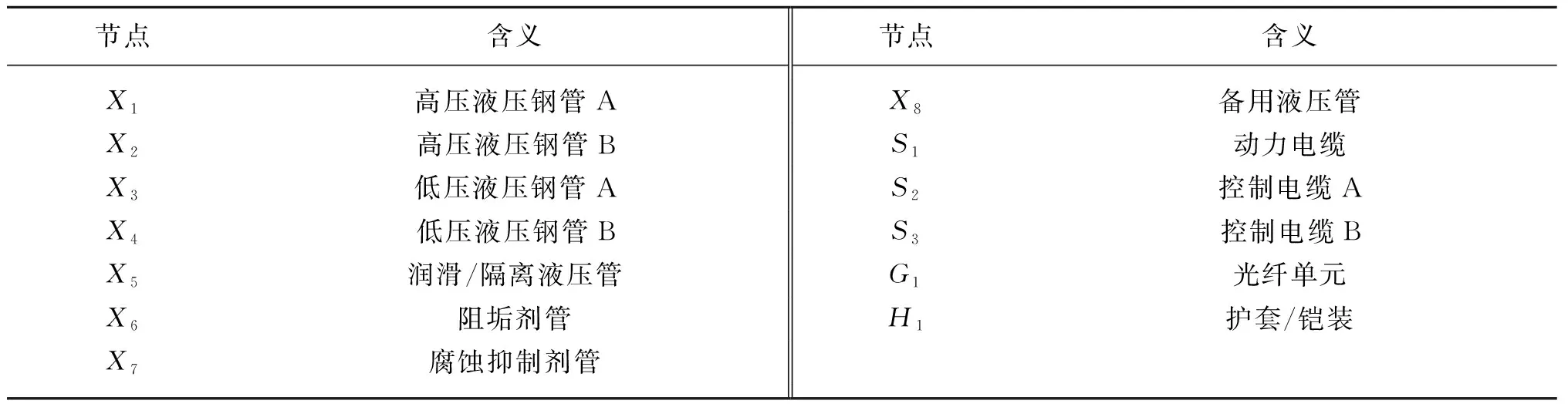
图2为某气田脐带缆截面，其中包括高压液压钢管(2个)、低压液压钢管(2个)、阻垢剂管、腐蚀抑制剂管、润滑/隔离液压管、备用管线、动力电缆、控制电缆、光纤以及最外层的护套/铠装[19]。为便于分析根据功用特点将所有部件划分为五个单元，即常用钢管单元、电缆单元、光缆单元、备用钢管单元以及护套/铠装。

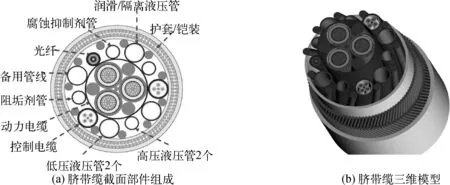
图2 目标脐带缆模型Fig. 2 The target umbilical

脐带缆在全寿命周期内会经历设计制造、储存、安装、在位运行以及修复等多个任务阶段。由于设计制造阶段的失效数据无从考证，修复阶段将在后文单独讨论，故主要研究广泛适用并且失效问题较明显的储存、安装以及在位运行阶段的可靠性，其过程具有以下特点：

1) 脐带缆的储存、安装以及在位运行任务阶段连续且不重叠。

2) 脐带缆自身复杂的结构与恶劣的工作条件决定了其在任务阶段内失效时无法立即进行修复。

3) 任意阶段任务的失效将导致整个任务的失效。例如脐带缆在安装过程中由于受到过大的弯曲载荷而导致关键部件破损，那么其在之后的在位运行期间将无法正常工作即失效。

以上特点符合PMS-BN方法的适用条件，由于故障树分析法具有描述故障的因果关系简单、直观、结构清晰等优点，首先使用故障树分析法建立失效模型，进而将其映射为BN模型，最后转化为PMS-BN模型进行可靠性分析。

根据脐带缆在工程应用中的失效案例总结[14]，在储存阶段，由于放在卷筒或转盘上的脐带缆受到弯曲载荷和挤压载荷，会造成液压管的弯曲失效和挤压失效包括常用钢管(5个)以及备用钢管。在安装阶段，铺管船将脐带缆慢慢铺设到海底，由于波浪流以及自重的作用，在顶部易引起液压管的拉伸失效；若安装船发生偏转时，在脐带缆的触底点容易发生护套/铠装的扭转失效。而在位运行阶段，在复杂载荷作用下容易发生受到自身重力、浮力等功能载荷以及波浪、海流、船体运动等环境载荷，会存在各种组成单元的失效，包括：常用钢管、备用钢管、护套/铠装、电缆单元以及光缆单元。

由脐带缆在三个阶段部件单元的失效特点，建立脐带缆在不同阶段最常见的失效模式的故障树模型，如图3所示。

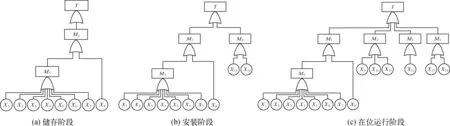
图3 不同阶段的脐带缆故障树模型Fig. 3 The fault tree analysis models of umbilical at different stages

多阶段系统的每个阶段可用离散时间贝叶斯网络(DTBN)作表述。这种用于表述阶段内部件相关性的DTBN称为阶段贝叶斯网络(phase-BN)，phase-BN由每个阶段的故障树模型转换得到。根据贝叶斯网络的基本原理, 将系统失效的故障树模型转化为phase-BN主要经过以下几步：

1) 建立与BN模型有关的变量及其解释。把脐带缆故障树模型中的基本事件对应到BN模型中的根节点。对故障树模型中的每个逻辑门, 在BN模型中建立相应的节点。

2) 建立有向无环图。根据逻辑门及脐带缆BN模型中相应的节点, 用有向弧连接根节点和各叶节点, 并表明父节点和子节点之间的关系。

3) 给定各个变量的条件概率, 生成BN模型的概率分布表。对相应的故障树模型，给出脐带缆BN模型根节点的先验概率，根据门的逻辑关系，生成相应的条件概率表[20]。

父节点的个数将在很大程度上影响PMS-BN的计算效率，故在建立贝叶斯网络模型时，应尽可能地将每个节点的父节点个数保持为2，这样可简化模型的复杂度。建立脐带缆在不同阶段的BN模型如图4所示。其中，故障树模型以及贝叶斯网络模型中的事件描述如表1所示。

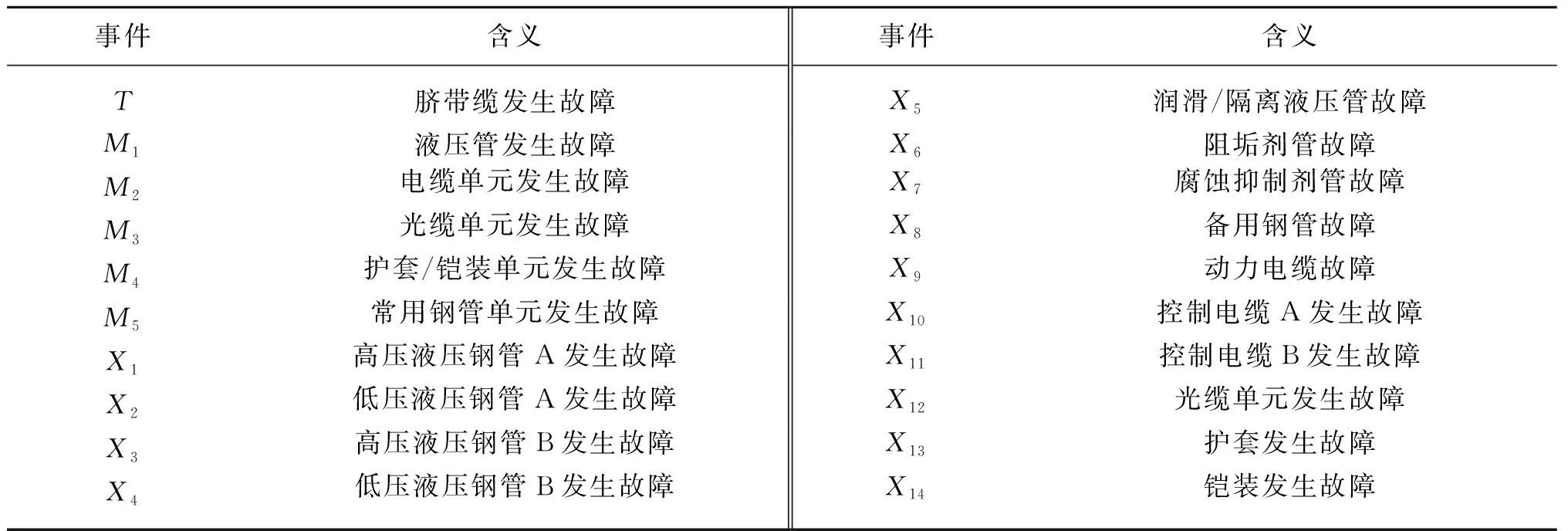
表1 故障树事件描述

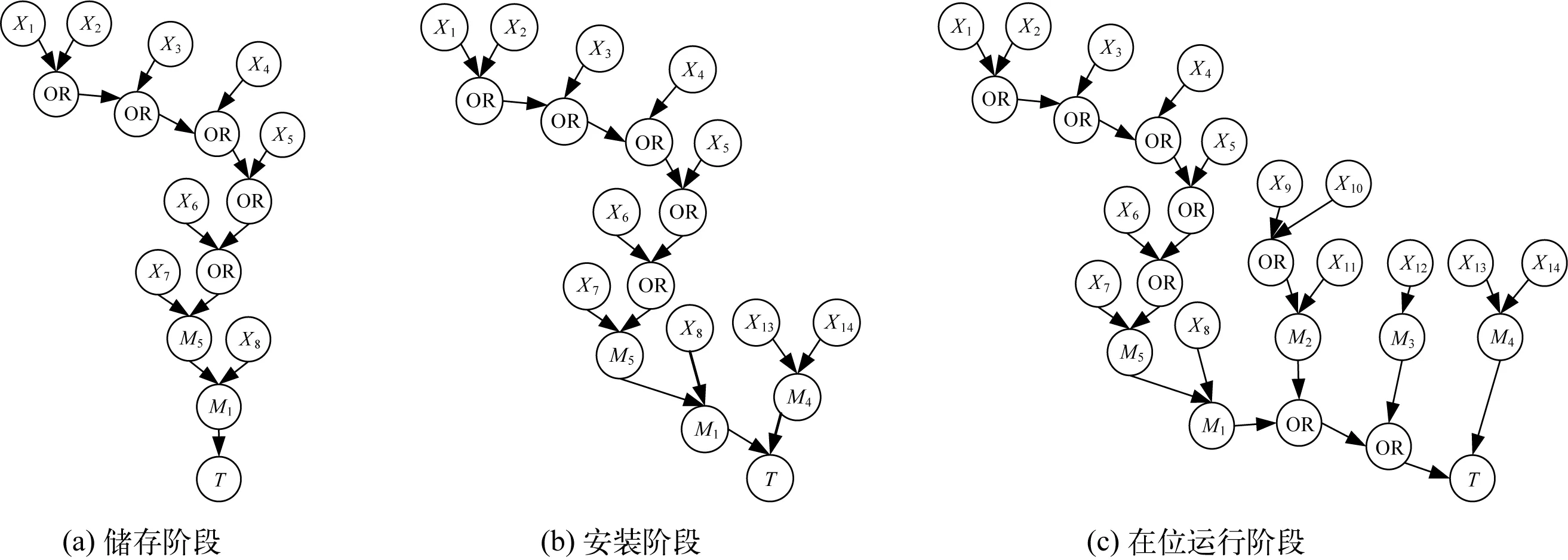
图4 不同阶段的脐带缆BN模型Fig. 4 BN models of umbilical at different stages

为了用多阶段贝叶斯网络描述整个脐带缆系统，通过以下两个步骤对phase-BN进行组合，建立PMS-BN模型：

1) 为描述同一部件在不同阶段的相关性，利用虚线有向边连接位于不同阶段但属于同一部件的节点。

2) 为表示整个PMS任务与各个阶段子任务的相关性，构建一个新的节点S表示整个系统的任务，并用有向边连接各个phase-BN的叶节点。S即代表了脐带缆系统的全阶段任务可靠度。

将上述各阶段的贝叶斯网络模型转化为PMS-BN模型，如图5所示。

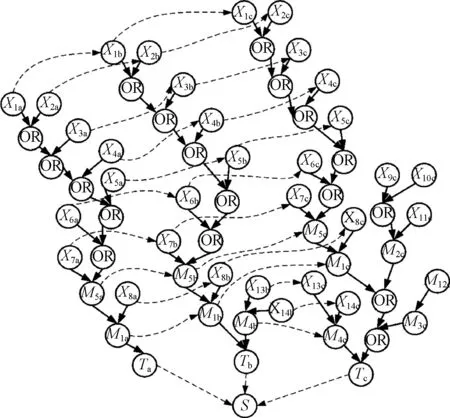
图5 脐带缆PMS-BN模型Fig. 5 The PMS-BN model of umbilical

依照上述过程生成脐带缆PMS-BN模型，Ta、Tb、Tc分别代表脐带缆储存阶段、安装阶段以及在位运行阶段的可靠度。Xna、Xnb、Xnc、Mna、Mnb、Mnc(n=1，2，……)分别表示各部件与单元在储存阶段的可靠度，下标a、b、c则表示节点所处的不同任务阶段。OR表示节点间的逻辑关系为或门。带虚线的有向边连接的是位于不同阶段但属于同一部件的节点，例如有向边连接的X1a、X1b、X1c表示同一部件节点X1处于不同任务阶段a、b、c。S即表示脐带缆系统在全任务周期内的可靠度。

假设所有部件的寿命服从指数分布，储存阶段、安装阶段以及在位运行阶段的时间长度分别为：Ta=2 a、Tb=1 a、Tc=18 a，每个时间阶段的单位长度δ=1 a，则m1=2、m2=1、m3=18。第一任务阶段的部件节点有m1+1个状态。前m1个状态表示部件在第m1个时间段中失效，而最后一个状态(m1+1)表示部件在第一阶段未发生失效。而在第二、第三阶段中，每个部件分别有m2+2、m3+2个状态，第1个状态表示部件在先前的任务阶段已经失效，接下来的m2(或m3)个状态表示部件在该任务阶段的第m2(或m3)个时间段失效，最后一个状态表示部件在该阶段未发生失效。

1.2 脐带缆可靠度计算

贝叶斯网络理论的核心内容是根据贝叶斯公式给出的条件概率定义：

(1)

式中：P(A)为先验概率，P(A|B)为后验概率。

根据贝叶斯网络的条件独立性假设和链式法则，贝叶斯网络的联合概率分布P(X1,X2,……，Xn)可以表示为各节点边缘概率的乘积。

(2)

式中：Xi为第i个贝叶斯网络节点，Pa(Xi)是第i个父节点[21]。

为计算PMS-BN可靠度，需计算父节点的先验概率以及其他节点的条件概率表。假设部件的寿命服从指数分布。对于指数分布，累积失效分布函数为：

F(t)=1-e-λt

(3)

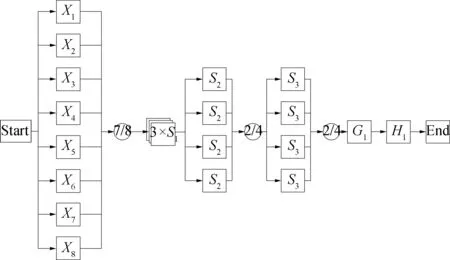
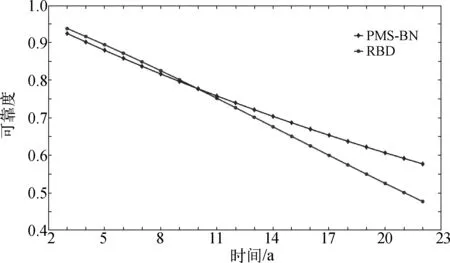
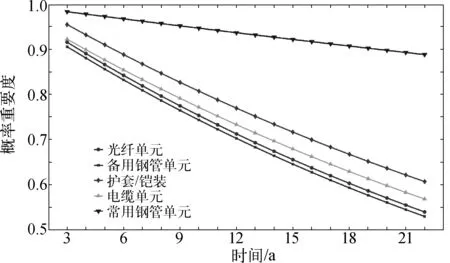
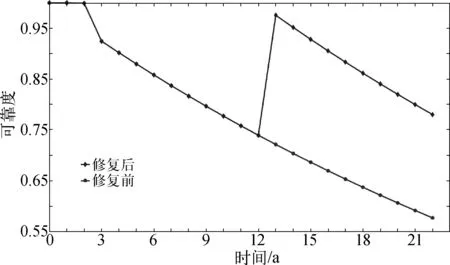
当父节点X1处于状态i(0

Pr{X1=i}=F(iδ)=1-e-λiδ

(4)

父节点X1处于状态m1+1的先验概率为：

(5)

其中，i<3，状态1表示失效，状态2表示未失效。

当某个部件在前一个阶段失效时，在接下来的阶段中它将不能继续工作。如果某部件在第一阶段的状态为1，2，……，m1，则该部件在第二阶段处于状态0的概率为1。对于X1或X2如果该部件在第一阶段没有失效，则在第二阶段该部件处于状态i的先验概率为：

(6)

由式(6)可知，部件X1(X2)在第二阶段处于状态i的条件概率等于部件X1(X2)在第一阶段处于相应时间段内的先验概率。同理，可得到其他阶段处于任意状态的条件概率，这是由指数分布的无记忆性决定的。

可靠性数据中的失效率是通过相似产品的类比、现场统计、工厂试验的结果以及参考可靠性分配值或工程经验得出的。OREDA是由数个国际石油企业共同编制的水下生产设备可靠性手册，具有相当权威性，根据OREDA手册[11]，各部件单元失效率系数λ如表2所示。

表2 部件单元的失效率系数

利用Matlab中BNT工具箱求解图5中PMS-BN，得到脐带缆在不同阶段的可靠度曲线如图6所示。

由图6可知，在储存阶段，其可靠度稳定于较高水平，与脐带缆处于仓库等较为稳定的环境有关；而在安装阶段，其可靠度下降明显，原因多为安装过程中可能存在的过度拖拽、弯曲半径过小等人工操作损害有关。在位运行阶段，可靠度变化近似呈随时间线性下降的趋势，其原因多与材料老化、腐蚀、疲劳以及风浪流等不确定性因素有关。在脐带缆投入使用第22年时，其可靠度约降低到57.70%。

将上述可靠性分析结果与可靠性框图法对脐带缆可靠性分析的结果进行对比。对目标脐带缆模型构造RBD模型如图7所示，RBD中各节点描述如表3所示，各单元的失效率同样采用ODEDA[14]数据。由于脐带缆在位运行阶段占据全寿命周期的绝大部分时间，将PMS-BN方法与RBD方法在位运行阶段的可靠度结果对比如图8所示。

图7 目标脐带缆可靠性框图模型Fig. 7 The RBD model of the target umbilical

表3 RBD模型各节点描述表

由图8可得，两种方法可靠度变化趋势基本一致，在脐带缆在位运行的前10年期间，两种方法可靠度结果基本一致。随着在位运行时间的增加，两种方法的计算结果的误差也逐步增加，在第22年时误差达到10%。原因在于RBD的方法中由于约束较强，其结果会比PMS-BN的计算结果更保守一些。

图8 PMS-BN与RBD可靠度结果对比Fig. 8 The reliability comparison between PMS-BN and RBD

1.3 重要度分析

重要度描述的是一个部件发生故障时对顶事件发生概率的影响。其中概率重要度反映的是各底事件状态对系统状态的影响程度：

(7)

由于脐带缆在位运行时间占据全周期寿命的大部分时间，其部件可靠性分析将更具说服性。对各部件单元进行概率重要度计算，得到各部件单元不同时刻概率重要度曲线如图9所示。

图9 各单元在位运行阶段的概率重要度Fig. 9 The probability of importance degrees of each unit at in-service time

由图9可知，在位运行阶段，目标脐带缆部件的重要度排序为：常用钢管单元、护套/铠装、电缆单元、光纤单元以及备用钢管单元。其中常用钢管单元始终处于重要度最高的地位；而其他部件重要度随时间下降速度较快，但重要顺序基本不变。

根据分析结果应在不同阶段采取相关措施对脐带缆进行预防与保护，如在设计阶段应考虑各材料的强度，尤其是钢管材料；对脐带缆整体应增加减拉部件，并对关键部位进行加固；安装时应避免过度拖拽等操作不当引起故障等；在运行期间应定期组织检查工作以保证脐带缆安全可靠运行等。

2 脐带缆修复后可靠度分析

脐带缆的设计寿命通常为15～25 a，根据数据世界上已有1 500多套脐带缆系统已运行15年或更久[22]，已达到或即将达到设计寿命。面对达到或即将达到设计寿命的脐带缆系统，分析其可靠性，从而决定对其进行维修或是更换，将是大量海洋石油企业面临的问题。PMS-BN方法适用于不可修系统，而对可修系统模型无法描述，故对PMS-BN方法进行了优化，通过引入条件可靠性，而不改变各阶段PMS-BN模型结构，使其拥有描述可修系统的能力。

条件可靠度是指一个系统在成功完成前一个任务后，再成功完成另一个任务的概率。在引入条件可靠度之前，先要提到条件概率。在概率论与数理统计中，假设A、B是两个事件，且P(A)>0,称

(8)

为事件A发生的条件下，事件B发生的条件概率。同理，假设R(T)表示系统成功运行T时间的概率，R(T+Δt)则表示系统成功运行T+Δt时间的概率，R(Δt|T)则表示系统在成功运行T时间的条件下，再成功运行Δt的概率，那么根据式(8)有

(9)

式(9)给出了条件可靠度的表达式。例如，对于前文所提目标脐带缆而言，假设在其成功运行至第12年时对其进行修复，那么其运行12年后的条件可靠度如表4所示，目标脐带缆修复前后可靠度对比如图10所示。

图10 修复前后可靠度对比Fig. 10 The reliability comparison between before and after umbilical repairing

表4 目标脐带缆的条件可靠度

通过引入条件可靠性，可以计算脐带缆修复之后的可靠度，评估它的剩余使用寿命。在第12年对目标脐带缆进行了修复，那么其再使用10年的可靠度为78.1%，比直接计算22年的可靠度高出了20%。这种结果的差异对脐带缆是否满足可靠性使用要求会有较大的影响，决定着其是继续使用、进行修复还是换新。

3 结 语

针对脐带缆全寿命周期的可靠性研究缺少的问题，提出了基于PMS-BN的脐带缆系统全寿命周期可靠性分析，得到脐带缆系统在三个阶段的可靠性变化情况和各部件在位运行期间的重要度变化情况。依靠贝叶斯网络描述故障逻辑关系非确定性能力与因果推理机制，增强了对脐带缆这种结构与失效原因复杂的系统可靠性分析以及故障风险规避能力，弥补了传统可靠性分析方法只能针对脐带缆某一种失效模式进行可靠性分析的局限性。得到如下结论：

1) 目标脐带缆在储存和安装阶段，可靠度并未出现明显的下降；在位运行阶段，可靠度变化近似呈线性下降。因此可进行在线温度、局部放电等检测与监测，以便尽早发现问题，降低故障概率。

2) 将本方法结果与RBD分析结果进行了对比验证，结果显示两种方法可靠性结果基本一致，在22年时间内误差在10%以内。原因在于RBD的方法中由于约束较强，其结果比PMS-BN的计算结果更为保守。

3) 目标脐带缆部件的重要度排序为：常用钢管单元、护套/铠装、电缆单元、光纤单元、备用钢管单元；随着年限的增长，常用钢管单元对目标脐带缆的可靠性影响最大，是脐带缆的薄弱环节，应采取措施进行预防与保护。

4) 通过引入条件可靠性对PMS-BN方法进行了优化，分析了脐带缆修复后可靠性变化情况，可为海洋石油企业决策是否继续使用、修复或是更换新脐带提供技术指导。