低雷诺数下圆柱强迫振动特性光滑粒子流体动力学模拟
2021-08-05赵宇蒙温鸿杰
赵宇蒙,温鸿杰,任 冰,王 超
(1. 大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024;2. 中国建筑股份有限公司,北京 100029;3. 华南理工大学 土木与交通学院,广东 广州 510641)
海流绕过海底电缆等管线类结构物流动时,柱体两侧发生交替泻涡现象,诱发结构物周期性振动,进而导致结构物疲劳损坏。前人研究发现,同等条件下柱体强迫振动和涡激振动时受到的流体力比较接近[1]。因此,开展柱体强迫振动问题研究,对于明确流致涡激振动特性具有重要的借鉴意义[2-3]。
目前,多位学者针对均匀流中的柱体强迫振动问题开展了大量的研究工作。其中,比较典型的工作如:1964年Bishop和Hassan[4]首先试验发现,当外界激励频率近似等于柱体自然泻涡频率时,结构所受到的升力急剧变大,同时升力与结构位移间的相位角也会出现跃变现象。Sarpkaya[5]将升力分解为两个分量,即惯性力和拖曳力,其中惯性力与振动加速度同向,拖曳力与振动速度同向。当与结构运动同相位时,拖曳力为激励力,流体向结构输送能量;反之,则表现为阻尼力,流体消耗结构能量。
在柱体强迫振动问题的研究中,除了结构受到的升阻力及其与结构位移间的相位差变化特性,振动过程中的频率锁定现象以及结构物下游的泻涡模式,也是研究人员重点关注的对象。1967年Koopmann[6]首次试验明确了圆柱体在低雷诺数情况下的锁定区间。Williamson和Roshko[7]进一步试验描述了结构后方的泻涡模式以及尾涡的形成、脱落和耗散全过程。Placzek等[8]等研究了雷诺数Re=100时圆柱强迫振动幅值与频率对泻涡模式的影响。基于有限元方法,赵静[9]研究了雷诺数Re=100和200以及10 000时的圆柱强迫振动规律,分析了流体力与结构振动频率间的相位关系、柱体强迫振动的锁定区间以及柱体后方的泻涡模式。梁亮文[10]数模研究了雷诺数Re=200时的圆柱强迫振动特性。
由于低雷诺数下柱体强迫振动物模试验对试验条件要求比较苛刻,实施难度较大。现有研究多是采用有限差分、有限体积等基于传统欧拉网格的数值模型来开展。这些模型往往需要引入繁琐的网格重构技术或使用浸入边界方法,来近似处理复杂的物面边界问题。而无网格光滑粒子流体动力学(SPH)方法,不受网格畸变影响,在处理具有复杂结构运动问题时具有很大优势。因为计算效率和计算精度的影响,目前采用SPH方法开展柱体强迫振动的研究文献不多,如Morris等[11]模拟了低雷诺数下圆柱绕流的速度场和压力场;Bouscassea等[12]模拟了雷诺数为180,佛罗德数在0.3到2.0之间的近自由表面圆柱绕流问题;Sun等[13]及Zhang等[14]研究了钝体绕流问题;Sun等[15]研究了柱体在激励频率为0.8倍其自然涡脱落频率时的振动特性。近年来,随着多种压力修正算法的提出以及并行计算技术的引入,基于SPH方法的水动力学模型的计算精度和计算效率均得到了显著提升。下文借助于DualSPHysic4.4开源代码,研究了激励频率对圆柱强迫振动特性的影响。
1 SPH数学模型
1.1 控制方程
水体看作是微可压缩流体,其运动控制方程可表述为下述形式:
(1)
(2)
式中:ρ,u,P分别是密度、速度和压力;g是重力加速度;υ0为动力黏滞系数。方程(1)和(2)可写为下述SPH离散形式:
(3)
(4)
Molteni和Colagrossi[16]提出的密度耗散项,可有效减小流体压力的非物理性震荡。引入密度耗散项的连续性方程可以表示为:
(5)
式中:δφ是可变参数,在文中δφ的值取为0.1[17],c0为参考声速。
流体压力可根据下式由密度变化率转化得到:
(6)
式中:γ=7,ρ0=1 000 kg/m3。
本模型使用Wendland[18]提出的五次函数作为核函数:
(7)
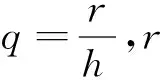
在使用SPH方法模拟强流场问题时,如果流体粒子分布不均,将导致压力场震荡,甚至在局部流场出现空腔等非物理性现象。为了增强流场的稳定性,Xu等[19]提出了粒子移位矫正法,该方法由Vacondio等[20]引入到了微可压缩SPH模型中。借鉴Lind等[21]的研究成果,粒子的移位距离δr可以表示为:
(8)

(9)
1.2 边界条件
如图1所示,计算域的左右两侧分别设置为入流和出流边界,通过采用开放边界算法来实现自由出入流边界,此算法由Tafuni等[23]提出。在入流边界和出流边界处各设置一个粒子缓冲区域,入流和出流缓冲区域内分别布置四层或更多层缓冲粒子。缓冲区粒子和流体粒子互相之间的转换具体表现为缓冲区的粒子在穿过缓冲区边界进入流体区域就会变为流体粒子而参与数值计算,反之,流体粒子穿过流体区域边界进入缓冲区内也会变为缓冲区粒子而不再参与计算。左、右两侧缓冲区内粒子速度采用不同的方法得到,左侧缓冲区粒子不设置垂向速度,只给定水平前进方向的速度U,而右侧缓冲区粒子的速度则是采用镜像方式得到,左、右两侧缓冲区内的粒子密度则均是采用镜像SPH插值获得。此外,本模型使用了核函数连续性修正算法[24]来解决镜像区域内局部流体粒子的支持域不完整的问题。

图1 出入流边界条件示意Fig. 1 Setup of outflow and inflow boundary conditions
上、下边界采用动边界条件[25]来模拟,为了减小原动力边界流体粒子与固壁粒子之间的排斥,采用Ren等[26]提出的修正方法对固壁粒子压力进行修正。本模型中上、下边界及圆柱分别设置两层固避边界粒子,其物理属性与流体粒子都是通过方程(1)和(2)的计算得到,但是不同情况下的固避边界粒子的物理属性又有差别,具体表现在:为了模拟自由滑移边界条件,上、下边界中的固避边界粒子速度给定其水平方向的速度固定为U,不设置垂向速度,密度值则是通过将固避粒子镜像到流体区域内进行插值而得到;固定圆柱中固避粒子的位移不更新,其速度值始终为0;强迫振动圆柱中的固避粒子速度根据最初的设定值保持不变,位移则根据设定的速度得到。
2 数值分析结果
2.1 计算域设置
如图2所示,本模型中坐标原点设置在圆心处,圆柱的直径为D=0.1 m,圆柱左边到入流边界的距离为10D,计算域的长度为60D,宽度为30D,可以足够保证边界对流场无明显影响。计算域的左、右两侧分别为入流边界和出流边界,其缓冲区内均设置为4层缓冲粒子。本模型在出口边界前方设置了垂向的人工阻尼层,宽度为5D,其作用在于通过减小流体粒子穿过右侧边界时的涡旋强度,来避免出口处强涡旋对计算域内压力场的影响。本模型中初始的粒子间距为Δx=D/50,固避粒子和流体粒子的总数之和超过4.6×106个。在计算开始前,给定流体粒子的初始水平速度为1 m/s,不设置初始垂向速度,初始密度值为ρ=103kg/m3。雷诺数的计算式为Re=UDυ0-1,不同雷诺数下的固定圆柱和振动圆柱的受力特性通过控制流场速度值不变,圆柱直径大小不变,只改变黏性值υ0来实现。每一工况的模拟时间均为30 s,运算时间在15.5 h左右,计算显卡型号为NVIDIA GeForce RTX 2080Ti。
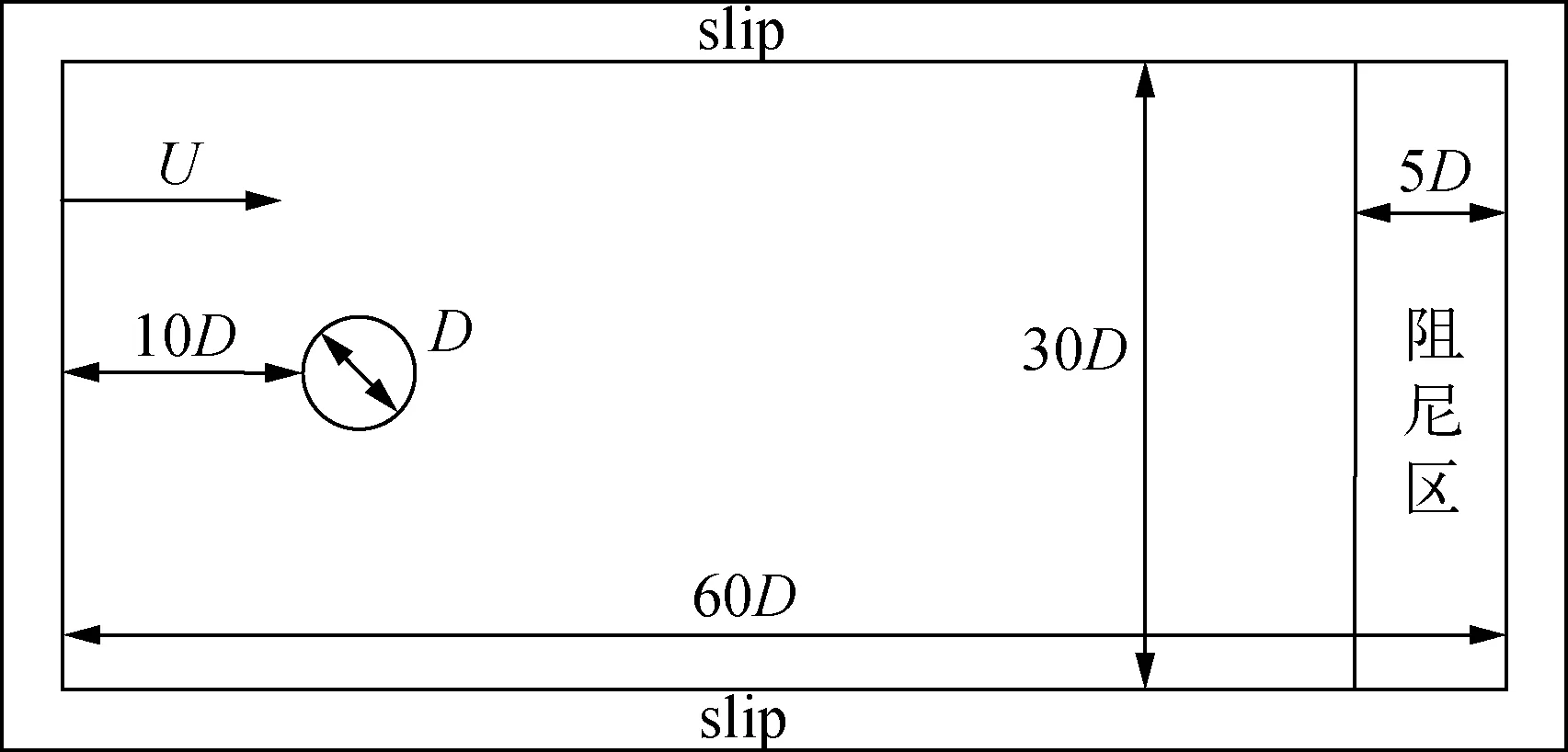
图2 计算区域示意Fig. 2 Setup of numerical computational domain
2.2 圆柱绕流
圆柱绕流计算域如图2所示。如表1所示,与前人的计算结果相比,本文计算得到的升力系数最值Clmax和斯特劳哈数St均吻合较好(St=fsD/U,fs为自然涡脱落频率,Ts为固定圆柱绕流的泻涡周期,即Ts=1/fs),但是阻力系数平均值Cdmean小于其他人的计算结果,Marrone等[27]也发现在采用与动力学边界相似的虚拟粒子边界时,圆柱的阻力系数会偏小。在粒子间距dp分别为D/67、D/50时,本文的计算结果变化非常小,说明粒子分辨率已经收敛。

表1 升力系数最大值Clmax、斯特劳哈数St和阻力系数均值Cdmean对比


图3 升力系数Cl和阻力系数Cd历时Fig. 3 Time series of the lift and drag coefficients

图4 计算域内压力场分布特征(Re=100)Fig. 4 Pressure field distribution characteristic map in computational domain(Re=100)

图5 右侧出口边界二个压力测点处压力历时曲线(Re=100)Fig. 5 Time series of the pressure at two measuring points on the outlet boundary(Re=100)
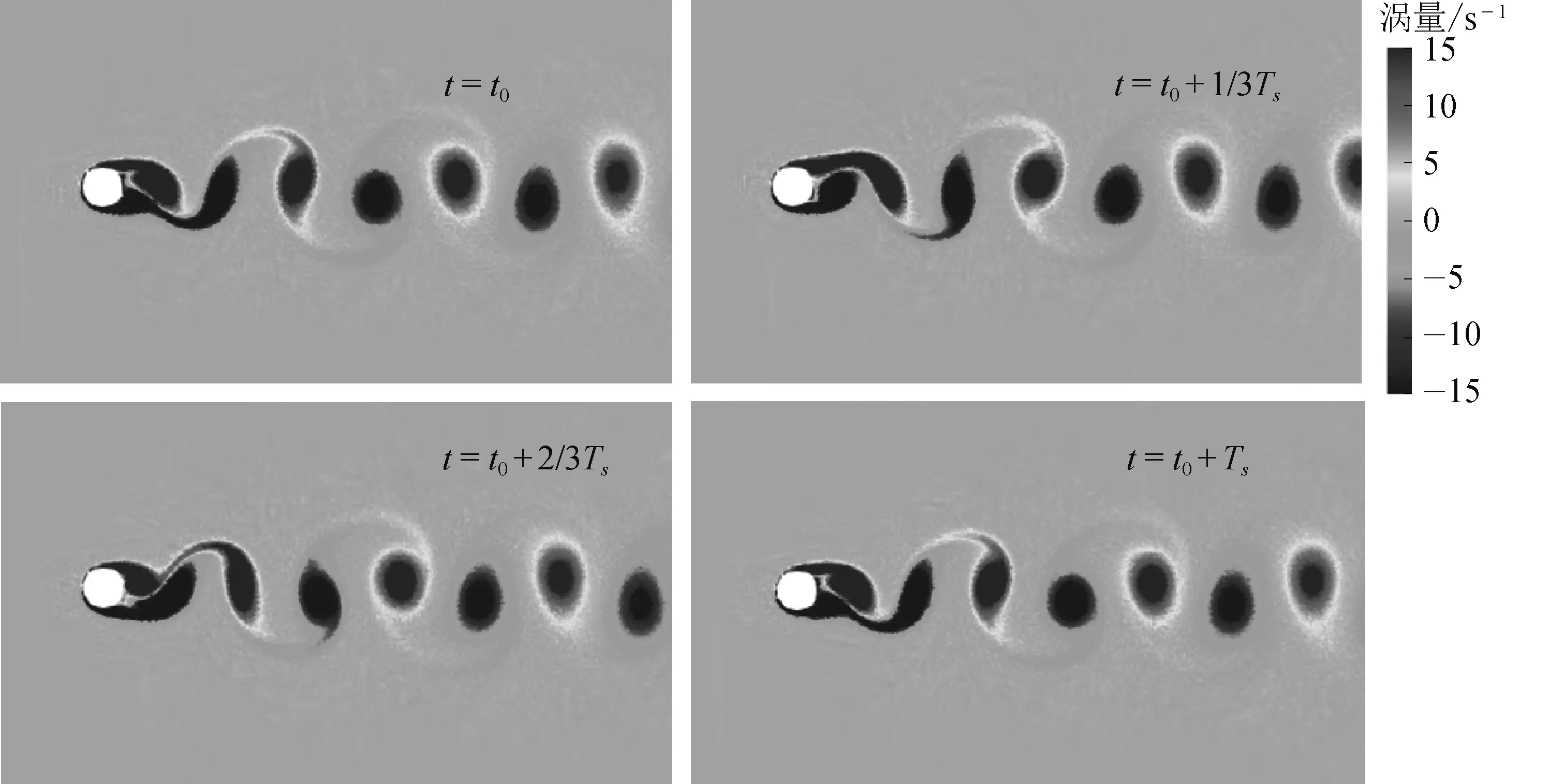
图6 一个周期内涡的形成、发展和脱落过程(Re=200)Fig. 6 The formation, development and shedding of vortices in a period
2.3 圆柱的强迫振动
通过模拟圆柱在雷诺数Re=100时的强迫振动问题,研究圆柱在不同激振频率下的尾涡脱落模式及其受力特性。文中,f0表示为激振频率,fv表示为升力频率,fs表示为自然涡脱落频率,圆柱振幅为A=ymax/D,其中ymax为圆柱的激振幅值。通过改变圆柱的激振频率f0模拟了当f0/fs=0.65~1.35之间共计8种工况下的圆柱强迫振动,当fv脱离fs,并且锁定在f0周围时,可以认为此时的圆柱位于锁定区间之内。
不同激振频率下的升阻力系数历时曲线及升力系数的振幅谱分别如图7的左图和右图所示。如图7(a)左图所示,即当f0/fs=0.65时,升力系数的拍频特征明显;从图7(a)右图也可明显看到两个峰值的结果,此时圆柱的强迫振动位于锁定区间之外。升力的主要频率成分有两个:一个靠近f0,另一个是fs,此时圆柱的升力同时由f0和fs控制,但fs起主要作用。当f0/fs=0.75时,从图7(b)右图可以看到升力已经主要由fs控制变为由f0控制,此时圆柱强迫振动已经位于锁定区间边界附近,当f0/fs=0.8、0.9、1.0、1.1时,从图7(c)、(d)、(e)、(f)右图可以观察到升力系数的振幅谱均只有一个峰值,升力系数的频率脱离fs,基本锁定于f0,圆柱的升力由f0控制,圆柱的强迫振动位于锁定区间。当f0/fs=1.2时,从图7(g)左图可以看到升力中也出现了拍频现象,右图的振幅谱也出现了两个峰值,但f0仍占主要成分,此时,强迫振动的圆柱即将脱离锁定区间。当f0/fs=1.35时,从图7(h)左图可以看出升力再次呈现拍频特征,图7(h)右图的振幅谱图也可明显观察到两个峰值的结果,此时圆柱的强迫振动已经超出其锁定范围。

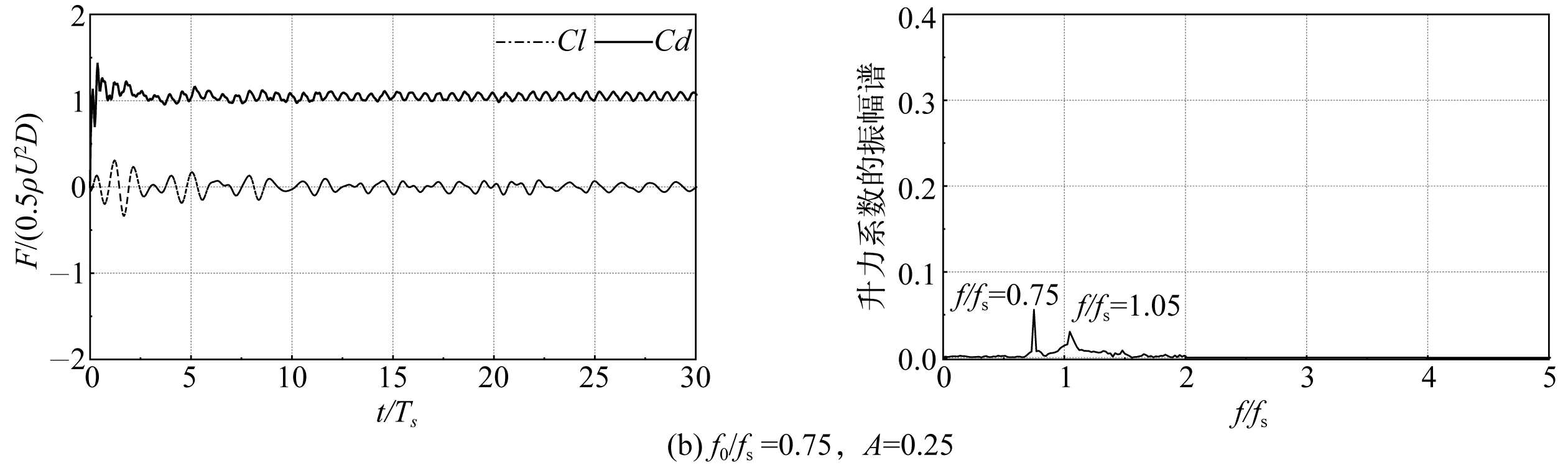

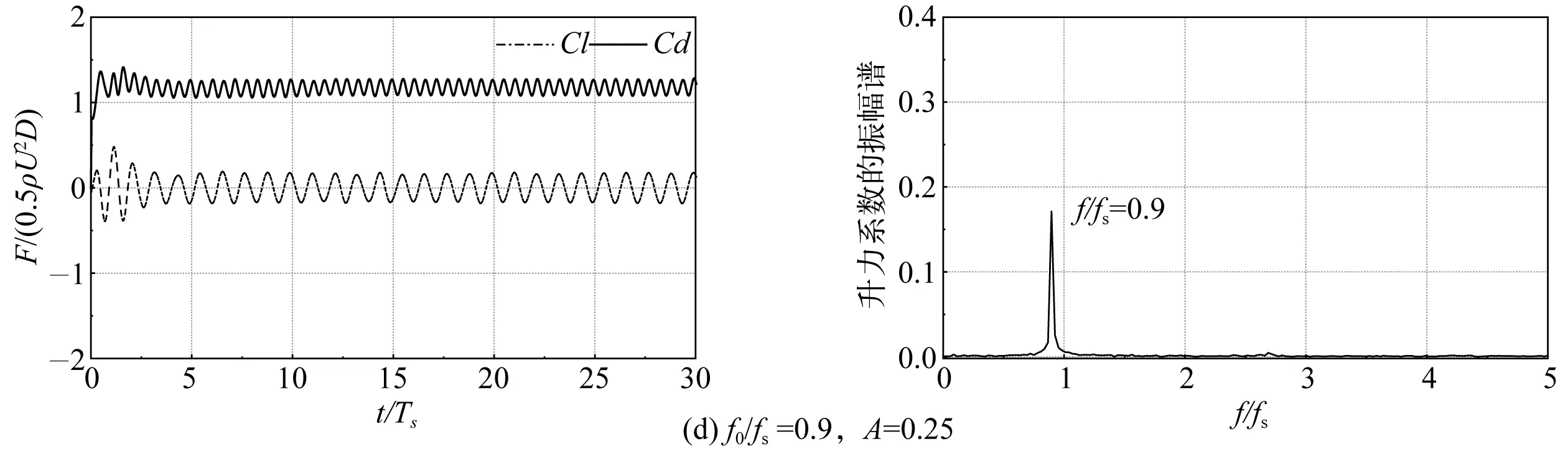
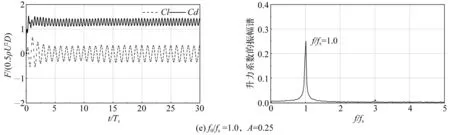



图7 圆柱在不同激振频率下的升阻力系数历时曲线和升力系数振幅谱(A=0.25, Re=100)Fig. 7 The lift and drag coefficients duration curve and lift coefficient amplitude spectrum of the cylinder under different excitation frequencies at Re=100, A=0.25
在振幅A=0.25,雷诺数Re=100时,强迫振动圆柱的锁定区间如图8所示,本文计算得到的锁定区间约为f0/fs=0.75~1.2,Koopmann[6]计算得到的锁定区间约为f0/fs=0.75~1.25,两者的计算结果基本趋于一致,差值在误差允许范围之内,且二者均在f0/fs=1.0两侧对称分布。

图8 A=0.25且Re=100时圆柱强迫振动的锁定区间Fig. 8 Locking interval of the forced oscillating cylinder at A=0.25, Re=100
经过计算发现,当f0/fs=0.8、0.9、1.0和1.1时,即在锁定区间内,圆柱的升力和垂向位移之间的实时相位角φ平均值分别为179.2°、123.6°、96.4°、59.2°。Placzek等[6]在当f0/fs=0.9、1.0和1.1时得到的相位角φ分别为113.8°、80.5°、47.7°,经过对比分析可知,两者中相位角φ的变化规律基本一致,即随着激振频率的减小而增大。
如图9所示,在锁定区间内,以激振频率比f0/fs=0.9、1.1为例,结构下游的泻涡模式均呈现出2S模式,在每个振动周期内,圆柱的上下两侧均各有一个涡脱落,这两个涡的强度一致、方向相反,但是当激振频率更大时,圆柱后方涡旋方向相同的涡会逐渐融合在一起。

图9 强迫振动圆柱处于锁定区间时计算域内的涡量场分布Fig. 9 Vorticity distributions in the computational domain when the oscillating cylinder is in the locked region
如图10所示,当振幅A=0.25且雷诺数Re=100时,升力系数的最大值Clmax随激振频率的变化规律与Placzek等[8]的计算结果基本趋于一致,均为先随着激振频率的增加先减小而后逐渐增大;阻力系数均值随激振频率的变化规律也基本相同,二者的均值Cdmean随激振频率的增加也均为先增加而后减小,在锁定区间左边界和右边界都取得极小值后再逐渐增大,虽然变化趋势相近,但是本文计算得到的阻力系数相比要更小,这是因为数值算法本身造成的差异,不影响对客观规律的揭示。

图10 圆柱升力系数的最大值Clmax和阻力系数的均值Cdmean随f0/fs的变化规律(A=0.25, Re=100)Fig. 10 Evolution of Clmax and Cdmean with the frequency ratio f0/fs at A=0.25, Re=100
3 结 语
基于GPU并行的DualSPHysic4.4开源代码,通过使用开边界算法来实现出入流边界,建立了基于SPH方法的数值水槽。通过对低雷诺数下圆柱绕流和圆柱强迫振动过程的数值计算,得到了以下结论:
1) 流体绕过固定圆柱,在低雷诺数的典型工况下,当雷诺数Re=100和200时,通过数值模拟得到的升阻力系数以及斯特劳哈数,与前人使用其他数值方法模拟得到的计算结果基本一致,显示SPH数值模型可以模拟低雷诺数下流体绕过固定圆柱后的圆柱受力特性及流场特征。
2) 流体绕过强迫振动圆柱,在低雷诺数的典型工况下,当雷诺数Re=100时,固定圆柱的振动幅值为A=0.25,强迫振动圆柱的锁定区间为激振频率比f0/fs=0.75~1.2,且此时升力系数极值随激励频率比f0/fs的增加而增大,阻力系数均值随激励频率比f0/fs的增加而先增大后减小,圆柱升力和垂向位移之间的相位角随激励频率比f0/fs的增加而减小。
