孤立波与升沉水平板相互作用数值模拟研究

纪巧玲，刘庆凯，徐成浩

(山东科技大学 交通学院，山东 青岛 266590)

水平板结构具有结构简单、安装方便、对环境影响小，适用水深范围广等特点，在波浪中迎浪面积小，受到波浪正面冲击的作用弱，大大减小了被损坏的可能性，被广泛用于透空式防波堤结构中[1-4]。对于固定在水下的平板，Brossard等[5]通过试验研究了单频波在水下固定平板的分解，指出单频波的能量转移到了板后高频谐波，相对板宽对能量转移有影响。王科等[6]在对浸没固定水平板的研究中指出，水平板上的浅水效应、透射波浪回流和板后波浪转化为高频谐波可以有效削减波浪。在固定水平板的基础上，双层水平板、圆弧板、复合结构等透空式消浪结构也被提出，并对这些结构的消浪性能及其影响因素进行研究，均取得了一定的成果[7-9]。

第一，新型农村合作医疗明确政府筹资机制。传统的农村合作医疗在政府的筹资机制方面模糊不清，未明确政府的职责权限。新型农村合作医疗制度明确实行“农民个人缴费、集体扶持和政府资助相结合的筹资机制，各级政府要根据实际需要和财力状况安排资金，按实际参加合作医疗的人数补助定额给与资助”。新农合在政府职责方面的明确为新农合制度的实施提供了前提条件。

水平板在水中的垂荡运动可以产生辐射波，在这种情况下，透过水平板的透射波将是辐射波和散射波的组合。辐射波和散射波的组合可以是正向相互叠加，也可以是相互破坏。因此，通过合理设计这种可动水平板的升沉系统，可以使辐射波和散射波尽量相互破坏，从而使透过水平板的透射波变小，获得优于同类固定水平板的工作效果。关于升沉板在防波堤方面的应用，Liu等[10]较早地提出了弹性支撑水平板可用于防波堤的概念，并基于势流理论，模拟升沉水平板在规则波中的运动，并对其作为防波堤的性能进行了研究，发现升沉水平板防波堤在临界刚度下波浪的透射系数可以降低到几乎为零，证明了这种结构在防波堤上的应用潜力。He等[11]认为势流理论不能有效模拟升沉板周围的涡旋变化，并采用光滑粒子流体动力学方法(smoothed particle hydrodynamics，简称SPH)并考虑流体黏性，研究连续波浪下不同潜深升沉板的消浪性能，结果表明大多数情况下升沉板的性能要好于固定水平板。王贤梦等[12]利用基于紧致插值曲线CIP方法的数值模型研究了规则波与升沉水平板的相互作用，分析了不同因素对于升沉水平板消浪性能的影响，分析得出规则波下升沉水平板主要通过能量反射、板上浅水变形和板两侧的涡脱落消能。目前关于水下升沉水平板与波浪相互作用的研究报道不多，且已有的研究大多集中在规则波上，对于升沉水平板的瞬态响应研究较少。

孤立波是一种可以用数学方法明确定义的单波，在固定的水深中具有比较稳定的波形，非常适合在理论和试验研究中使用，利用孤立波可以更加清晰地了解水平板在不同时刻的瞬态响应及对周围流场的影响。为进一步探寻升沉水平板的消浪机理与不同影响因素下的水动力变化规律，基于考虑流体黏性的二维不可压缩N-S方程，以高阶紧致插值CIP方法离散并求解流动方程，采用VOF方法重构自由液面，构建二维数值波浪水槽。针对完全浸没在水中的单层升沉水平板，开展孤立波与升沉水平板相互作用的数值模拟研究，分析升沉水平板在波浪中的运动特性以及板上波浪的变化规律，并研究影响升沉水平板消浪性能的因素，为升沉水平板应用和进一步研究提供参考。

1 数值方法

1.1 控制方程

数值模型研究气—液—固三相耦合下的流动问题，以二维不可压缩N-S方程为控制方程：

(1)

(2)

垂荡运动的相对振幅AR与最大相对速度Vm随相对刚度K*的变化趋势基本相同，都是先增加后减小。当K*=0.5时，相对振幅AR和最大相对速度Vm均取得最大值(AR=0.67和Vm=0.029)。从图6中可看出，相对振幅AR和最大相对速度Vm存在正相关关系，相对振幅AR的增减也会伴随着最大相对速度Vm的增减。当K*=4.0，即透射系数Ct取得最小值的情况下，对应的相对振幅AR=0.23，最大相对速度Vm=0.013，此时的运动响应并非极值，可见升沉板的运动响应控制在合理的范围内才能取得良好的消浪效果。

4.4 注意保暖 由于手术时间较长，术中失血较多，应给予患者必要的保暖措施，以减低心血管并发症的风险，减少患者术后苏醒时间。

1995年，建设部印发了《城市园林绿化企业资质管理办法》和《城市园林绿化企业资质标准》，将园林绿化企业自此从建工企业中分离。2007年，建设部印发了《工程设计资质标准》，又将风景园林工程从市政公用行业脱离出来。2011年3月，风景园林学被批准为国家一级学科，与城乡规划学、建筑学形成三足鼎立之势，风景园林行业的地位产生了巨大提升。但目前的城乡园林绿化法规大多仍然设置在城市市政公用事业规体系之下，在生态文明建设日益重要的今天，缺乏一定的独立性。

(3)

式中：φi(i=1,2,3)为气、液、固三相的体积函数，三者满足关系φ1+φ2+φ3=1，求得φi以后可以进一步求解单个计算网格中的流体属性。

1.2 流固耦合方法

浸入边界法(immersed boundary method，简称IBM)[13]被用来处理流固耦合问题，在离散的N-S方程中加入虚拟的力源项，用来表示结构对流体的影响:

水汽是产生暴雨的必要条件,水汽通量是表征水汽输送的重要物理量,它表示单位时间内流经某一单位面积的水汽含量,代表水汽水平输送的强度,物理意义为每秒钟对于垂直于风向、一厘米宽、一百帕高的截面所流过的水汽克数[14]。水汽通量通常用来判断水汽来源、水汽的输送方向和强度以及与环境的关系。从850 hPa水汽通量和风场图(图3)可见,“尼伯特”台风在苍南地区引发的暴雨过程水汽由强东南风急流输送,来自东海的水汽通量最高达20 g/(s·hPa·cm),苍南又在台风倒槽曲率最大处附近,可引起大量水汽在该地辐合。

(4)

值得注意的是，其他条件的情况下，K*<2.0时的升沉板的透射系数要大于水平板固定时的透射系数。板的运动会产生辐射波，辐射波与散射波相互作用可以加强或者减弱孤立波的波高，这种加强或者减弱主要取决于辐射波的强度和散射波与辐射波之间的相位差，辐射波的强度主要取决于板的运动状态，辐射波与散射波的相位差也和升沉板的运动状态相关。从图6中可以看到，相对刚度K*对板运动状态影响较大，因此合理的支撑刚度选择也是十分重要的。

1.3 求解方法

然而，她的蛮横霸道、争强要胜，随着年龄的增大并没有减轻，反而越来越严重，很多时候让他觉得不可理喻。他也不是个软弱的人，有时被逼急了，他们会发生激烈地争吵，甚至大打出手，并最终以女孩的全面胜出宣布结束。他并非打不过她，只不过，年龄上大了一岁半，他的心理上，却似乎比她成熟得多。

2 模型验证

2.1 模型布置

Lo等[17]利用数值模拟和模型试验结合的方式，研究了孤立波在固定水平板上的传播特性，并测量了板上和前后的波高。为了验证数值模型的可靠性，采用参数相同的二维数值模型对试验进行建模。图1为根据试验构建的数值波浪水槽，采用二维正交笛卡尔坐标系，以静止水面为z轴起点，波浪前进方向为x轴正向。水槽中恒定深度区域长度为11 m，恒定水深h=0.2 m，在恒定区域中间安放了一块板宽B=1.156 m，厚度δ=0.01 m 的水平板。在数值水槽的后方设置有消波区，用以消除波浪反射。四个数值波高仪G1-G4用来测量波形，其中波高仪G2，G3被放置在固定位置，G1，G4的位置随波长变化，距离板的边缘为四分之一个波长。

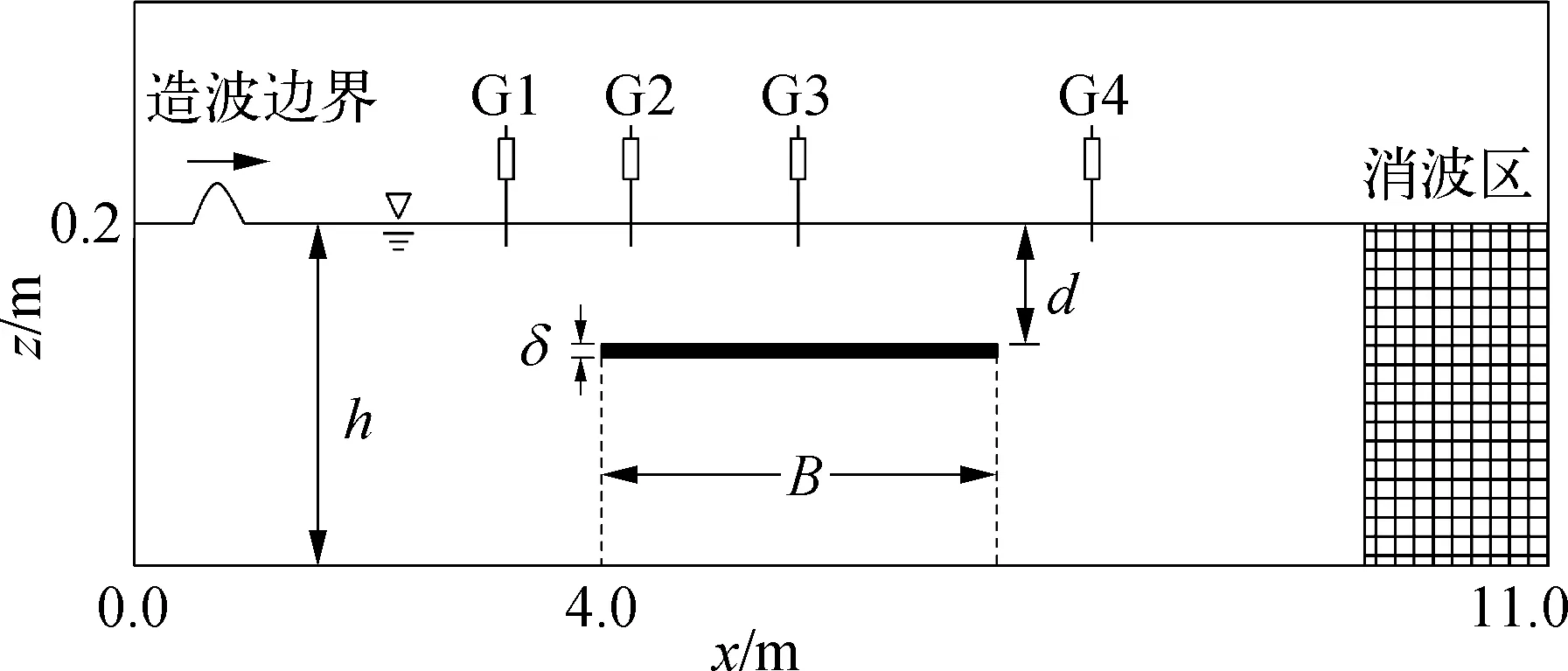
图1 固定板在二维数值水槽中的布置Fig. 1 Arrangement of the fixed plate in a two dimensional numerical flume

在数值模型中，要求孤立波波形在传播的过程中保持稳定，基于Lee等[18]三阶孤立波理论，采用速度边界法造波。为验证数值模型在非线性波下的适用性，选取非线性较强(H/h=0.2)的工况，见表1。其中，孤立波的波长L和周期T为有效波长和有效周期[19]，定义为：

表1 固定板工况参数

(5)

(6)

式中：H为孤立波波高，c为孤立波波速。

模型在笛卡尔二维正交坐标系下建立，采用分步法求解N-S方程。以CIP方法[14-15]离散对流项，以中心差分法求解扩散项，以SOR(successive over relaxation method)方法求解压力项，自由面重构采用VOF类型的THINC/SW(tangent of hyperbola for interface capturing with slope weighting)方法[16]，运用双曲正切函数构造水气两相界面并计算通量，具有准确性好，求解效率高的特点。

为处理在单个网格内的多相问题，采用基于多相流理论的VOF方法，引入体积函数：

2.2 验证结果

将波面高程η和时间t进行标准化，记为η/H和t/T，用标准化后的数据比较验证。在验证模型处理孤立波与结构相互耦合的能力之前，首先验证黏性数值模型的孤立波造波的准确性。在空水槽的情况下，选取G1和G4数值波高仪的数据，对比数值波形与理论波形。图2为设定工况下数值波形与理论波形的对比，波峰经过时刻t/T=0，图中虚线为数值波高仪测得波面变化数据，实线为理论值。总体来说，数值模型产生的孤立波波形与理论值基本相符，波高误差控制在一个网格内(dy=0.001 m)，波高衰减率小于3%H，说明孤立波在传播过程中可以保持波形稳定，基本无衰减。

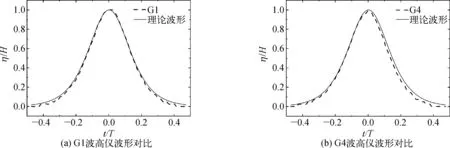
图2 数值模型与理论值波形对比Fig. 2 Waveform comparisons between numerical model and theoretical value

图3为G1-G4数值波高仪测量的波面高程历时变化，并与Lo等[17]的试验数据进行了比较，规定波峰经过G2波高仪时t/T=0。可以看到，G1波高仪测得的到达板前的孤立波波高，数值结果要高于试验测量值，试验中的波浪耗散可能会导致这种问题。试验和数值结果在波尾处的振荡趋势存在微小差异，但所有情况下总体趋势及数据吻合较好，可以较为准确地表达孤立波的变化情况。

图3 波面高程变化历时对比 Fig. 3 Comparisons of time history curve of wave surface elevation

3 升沉水平板的数值模拟

3.1 数值模型布置

升沉水平板在二维数值水槽中的布置见图4，与固定板在水槽中的布置相似，模型采用二维正交笛卡尔坐标系，坐标原点位于数值水槽模型最左侧静水面处，x轴正向水平向右(波浪前进方向)，z轴竖直向上为正向。水槽中静止恒定水深h=0.2 m，在水槽的最右侧设有消波区。水槽中部放置一块水平板，沿水平方向板宽B=1.156 m，板厚δ=0.01 m，底部采用一根刚度为K的弹簧与水槽底部相连，在初始时刻，作用在板上的静水压力与板自身的重力达到平衡，升沉板处于静止状态。水平板的潜深(板上侧表面到静止水面的距离)为d，升沉板左侧边缘距离造波边界为8 m。沿水平方向布置有6个波高仪，其中G1和G6数值波高仪与板边缘之间距离均大于一倍波长，可以测得比较稳定的波形，避免结构物的影响。

图4 升沉板在二维数值水槽中的布置 Fig. 4 Arrangement of the heave plate in a two dimensional numerical flume

考虑相对刚度K*(K*=K/(ρWgB2))，相对潜深d/h，相对波高H/h等影响因素，设计不同工况，相对波高H/h探究升沉水平板在不同影响因素下的消浪性能以及运动响应，表2为具体模拟工况。其中相对波高H/h=0.25为数值模型正确生成孤立波的极限值，增加相对波高H/h将无法得到目标孤立波，选取的相对波高H/h范围和其他研究孤立波与近海结构物相互作用的试验和数值分析选取范围相似[20-21]。

表2 数值分析工况设计

3.2 数据处理

采用透射系数Ct来衡量升沉水平板的消波能力。Case 2工况中相对潜深d/h=0.1以及d/h=0.5时G6号数值波高仪记录的波面变化数据见图5，波峰经过G2波高仪的时刻为初始时刻(t/T=0)，可以看到，不同工况下G6波高仪记录的波面变化是存在差异的，当d/h=0.1时波面历时存在双峰现象，这说明波面未完全演化完成，d/h=0.5时，波面演化较为成熟，仅存在孤立波的单峰，两种情况均存在不规则的尾波振荡。为统一计算标准，选择最高波峰对应波高作为透射波高，透射系数Ct计算公式为：

图5 不同相对潜深d/h波面变化历时(G6) Fig. 5 Time history curves of wave surface with different relative depth d/h (G6)

(7)

式中：Ct为透射系数，η6为G6数值波高仪测得透射波高，H为孤立波波高。

当水平板与孤立波相互作用时，板对波的响应可以采用板的相对振幅AR以及相对运动速度Vc表示，两者的计算公式为：

AR=AP/H

(8)

(9)

式中：AP为板的测量振幅(板运动最高点和最低点之间的距离)，H为孤立波的波高，V为板的测量运动速度，g为重力加速度，h为水槽的静止水深。

4 结果分析

4.1 相对刚度K*的影响

升沉水平板通过弹簧与水槽底部相连接，升沉板在水中运动的状态与弹簧的刚度有关。选取表2中Case 1工况，分析相对刚度K*对升沉板与孤立波相互作用的影响。图6为板的透射系数Ct、相对振幅AR以及最大相对速度Vm(相对速度Vc的最大值的绝对值，不考虑方向)随相对刚度K*的变化趋势,横坐标采用对数坐标表示。首先可以观察到，当K*=50时，板的相对振幅AR和最大相对速度Vm均接近于0，可以近似看作固定板的情形，此时透射系数Ct=0.65。透射系数Ct随相对刚度的增加呈现先减小后增大的趋势，当K*<4.0时，透射系数Ct随相对刚度K*的增加而减小；当K*>4.0时，透射系数Ct随相对刚度K*的增加而增大，且增大趋势逐渐放缓；当K*=4.0时，透射系数取得最小值Ct=0.52。在其他条件相同时，K*=4.0的升沉板的透射系数要比固定板减小约20%，此时升沉板消浪性能要更强。

管理会计的工作较为灵活，工作中没有固定的规范准则，为了将管理会计所具有的的优势充分发挥，就应当重视审计监督。合同管理是企业中财务管理部分的重中之重，企业应当从管理会计的角度出发，分析历史合同中，执行环节存在的问题和相应的责任主体。并且以过去的财务管理体系为基础，对合同管理模式进行调整。最终构建起一套新的财务管理体系。

式中：u为速度矢量，ρ为液体密度，p为压强，μ为动力黏度系数，F为质量力。

式中：L为虚拟的力源项。为研究水平板在波浪作用下的升沉运动特性，本模型假定水平板只作垂向上的单自由度运动，可以简化计算过程，提高计算效率。

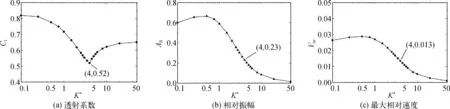
图6 透射系数Ct、相对振幅AR以及最大相对速度Vm随相对刚度K*变化Fig. 6 Variations of transmission coefficient Ct, relative amplitude AR and maximum relative velocity Vm with relative stiffness K*

4.2 流场分析

根据前文的分析可知，当K*=4.0时，升沉板透射系数Ct取得最小值，此时的消浪效果最好。因此选取表2中Case 1中相对刚度K*=4.0的工况，分析升沉板不同时刻周围流场的分布情形，从而具体研究水平板对孤立波的消浪机理。图7为该工况下升沉板运动历时曲线，横坐标为标准化后的时间t/T，以波峰经过G2波高仪的时刻为初始时刻(t/T=0)，纵坐标为板的相对位移y/H。从图中可以观察到，水平板与孤立波相互作用是非线性的，板的运动中包含高频响应。板会经历一个先上升后下降的运动，随后会经历振幅逐渐衰减的非线性自由振动，直至恢复平稳状态，偏离初始位置的最大位移出现在负方向。通过观察板运动的历时曲线，选择6个有代表性的时刻绘制流场图进行分析，各个时刻点(a,b,c,d,e,f)的位置分布在图7中已经标出，其中a,c,e为升沉板回到初始位置的时刻，b,d,f为升沉板的运动到达极值的时刻。

（6）工作透明化与站立会议。最常见的做法是准备一块白板，上面分成三栏：待办事项、在办事项、完成事项。把待办事项写到便笺纸上，随着进度的推进，将相应的便笺纸转移到其他栏目。团队每天在固定时间进行内部沟通，时间一般不超过15分钟，且站立进行，敏捷主管向团队成员提出下列问题：你昨天做了什么去帮助团队完成冲刺？今天你打算做什么来帮助团队完成冲刺？什么因素阻碍了团队的前进之路？

图7 升沉板运动历时曲线(Case 1, K*=4)Fig. 7 The time history curve of the motion of the heave plate (Case 1, K*=4)

根据前面的分析，升沉板对于孤立波的削弱是一个动态平衡的过程，这个过程中存在着能量之间的多次转化，涉及到涡旋脱落，波浪变形与破碎，波浪反射以及辐射波的产生。第一，在板的两侧边缘会出现涡旋的产生与脱落，复杂的涡流紊动会消耗大量的孤立波能量；第二，孤立波在经过平板上方时，会出现浅水变形以及波浪的破碎，在板的后端还会出现波浪反射，同样会消耗部分的波浪能量；第三，板在孤立波的作用下会发生受迫振动，板的振动会引起辐射波，孤立波的能量转化为辐射波的能量，从而分散波浪能量，生成辐射波也会与孤立波相互作用，进一步消减波浪。

图8 不同时刻升沉板周围流场状态(Case 1, K*=4)Fig. 8 Flow fields around the heave plate at different time (Case 1, K*=4)

值得注意的是，孤立波与升沉板相互作用整个过程中，只是在板的边缘以及板的上方出现了复杂的流场变化，板下方的水流保持一种近似均匀分布的流动现象，水流的方向和板运动的速度方向有关，当板运动到极值点时(b,d)，此时板的运动速度接近零，板下水体表现为水平流动的状态；当板运动回到初始位置时(c,e)，板下水流不再水平流动，而是近似垂向流动，其方向与板的垂荡方向一致。这种现象说明板下方水体不易受到扰动，但板上下运动使得板边缘周围的水体更容易受到扰动，形成复杂的紊动涡流区域。

升沉板在不同时刻的流场分布见图8。当板开始运动时(a)，孤立波的波尾到达板的左侧边缘附近，板左侧边缘水体受到扰动并出现紊流，而板右侧的水体此时几乎不受影响；当板到达向上的最大位移时(b)，波峰到达板的左侧边缘上方，板左侧上方微小的扰动发展成一个非常明显的顺时针涡旋，板的右侧边缘出现紊流并开始产生涡旋，此时由于板的抬升，已经到达板上方的部分波浪被抬高，开始出现浅水变形；当板回到初始位置时(c)，此时波峰大约到达板中心上方，板左侧上方有顺时针涡旋脱落，右侧上方形成明显的逆时针涡旋，尺寸要大于左侧的顺时针涡旋，板右侧边缘存在较大的紊流区域。波浪继续变形，波前变陡，涡旋的生成与脱落以及波浪的浅水变形都将耗散波浪的能量。同时，在板右侧上方的水体上出现了板运动引起的辐射波，波高远小于孤立波，辐射波的生成会分散孤立波的能量；当板到达向下的最大位移时(d)，可以观察到板左侧边缘上方的顺时针涡旋继续脱落，左侧边缘下方的水体也开始出现逆时针涡旋，同时板右侧边缘上方也发生了顺时针涡旋脱落现象，由于板潜深的增加，浅水变形会稍微变弱。此时波峰到达板右侧边缘附近，波峰变尖而且波形变陡，出现波浪破碎，散射波与辐射波相互叠加，叠加波的波高超过了入射波高，板右侧脱落的涡旋与破碎的波浪相互作用，形成了复杂涡流区，进一步消耗了波浪能量；当板再次回到初始位置时(e)，在板左侧边缘的上方存在顺时针涡旋脱落，下方出现了逆时针涡旋脱落，下方涡旋尺寸要大于上方涡旋尺寸。在板的右侧边缘上方复杂涡流区仍然存在，右侧边缘下方形成了一个尺寸较大的顺时针涡旋。此时波峰离开平板，透射波的波高明显减小，波形也变得平缓。在板的上方出现了向后传播的反射波，此时反射波还未与入射波完全分离，板上方形成了一个波包的形状。反射波的出现说明在板的后端存在波浪反射，反射波会带走波浪的部分能量，同时也会与板相互作用，影响板的运动状态；当孤立波离开板上方时(f)，升沉板会继续非线性自由振动，此时板的振幅已经大大减小，在板的两侧边缘仍然会出现较小的涡流区，水面上存在许多向两侧传播的高频谐波，这些高频谐波主要是板自由振动引起的辐射波，以板中心分界向两侧传播。板的振幅会逐渐变小，水面的高频谐波也会逐渐消失。在这个过程中，板将来自孤立波的能量转化为辐射波的能量，孤立波的能量得到削弱。

“数学教育中的历史与认识论欧洲暑期大学”（European Summer University on the History and Epistemology in Mathe- matics Education，简称 ESU）是数学史与数学教学的关系（简称HPM）国际研究小组最重要的活动之一，每4年召开一次．第八届“数学教育中的历史与认识论欧洲暑期大学（简称ESU-8）于2018年7月20—24日在挪威奥斯陆城市大学举行．曾任HPM国际研究小组主席的Constantinos Tzanakis、EvelyIle Barbin 及奥斯陆城市大学的Bjørn Smestad等组织了此次会议．

4.3 相对潜深d/h的影响

选取表2中Case 2工况，分析相对潜深d/h对升沉板消浪能力与运动响应的影响。图9为透射系数Ct、相对振幅AR和最大相对速度Vm随着相对潜深d/h变化趋势。

图9 透射系数Ct、相对振幅AR和最大相对速度Vm随相对潜深d/h变化Fig. 9 Variations of transmission coefficient Ct, relative amplitude AR and maximum relative velocity Vm with relative depth d/h

可以看到，透射系数Ct呈现先减小后增大的变化趋势，当相对潜深d/h=0.25时，透射系数取得最小值Ct=0.52。当相对潜深d/h=0.5时，此时透射系数Ct=0.70，相对于相对潜深d/h=0.25时提高了约37%。潜深的增加会导致浅水变形的减弱，过低的潜深的浅水变形能力虽然变强，但是涡旋脱落又会减弱，这两种情况都不利于升沉板对孤立波的削弱。可见，升沉板的潜深需要控制在合理的范围内，过大或者过小的潜深对升沉板的消浪性能都存在不利影响。相对振幅AR和最大相对速度Vm的变化趋势基本相同，都呈现先增加后减小的趋势，当相对潜深d/h=0.25时，两者均取得最大值，此时相对振幅AR=0.23，最大相对速度Vm=0.014。但总体来说，潜深对孤立波作用下升沉板的运动响应影响不大。

4.4 相对波高H/h的影响

实际环境中波浪的波高是复杂多变的,因此需要研究升沉板在不同波高下的适用性。选取表2中的Case 3工况，分析不同相对波高H/h对升沉板的消浪性能和运动响应的影响。图10给出了板的透射系数Ct、相对振幅AR和最大相对速度Vm随相对波高H/h的变化趋势。图中，随着相对波高H/h的增加，透射系数Ct随着相对波高H/h的增加逐渐减小，且减小的趋势逐渐变缓。这说明在一定的波高范围内，升沉板对波高较大的孤立波的削减作用更好。相对振幅AR和最大相对速度Vm随着相对波高H/h的增加而增加，但变化趋势有所不同，相对振幅AR的增长趋势比较平缓，最大相对速度Vm变化趋势的线性特征更加明显，当相对波高H/h增加一倍时，最大相对速度Vm大约增加3.6倍。一定范围内波高的增加会引起板运动速度的增大，有更多的波浪能量转化为板的机械能，也会引起更为激烈的涡流脱落和更大的紊流区域，有利于波浪能量的衰减。

2.完善以合同管理为核心的管理机制，建立严格完整的合同管理流程。油田企业要实现合同管理规范化、科学化、制度化，有效防范经营风险，就必须增强一体化管理意识，进一步规范和强化合同全过程管理，建立以合同管理为核心的管理机制，理顺各方面关系，建立和完善“四个对接”、“四个规范”、“四个细化”为主要内容的合同管理体系，建立严格完整的合同管理工作程序，提高合同签订质量及“签约及时率”。

图10 透射系数Ct、相对振幅AR和最大相对速度Vm随相对波高H/h变化Fig. 10 Variations of transmission coefficient Ct, relative amplitude AR and maximum relative velocity Vm with relative wave height H/h

5 结 语

基于二维不可压缩N-S方程，采用紧致插值曲线CIP方法和VOF法构建二维数值模型，并进行验证。运用数值模型开展孤立波与升沉水平板相互作用的研究，通过分析不同瞬态板周围流场探寻升沉板的消浪机理，并研究了相对刚度K*、相对潜深d/h和相对波高H/h对升沉板消浪性能和运动响应的影响。得到如下结论：

1) 其他条件相同的情况下，存在最佳相对刚度K*=4.0，此时升沉板对孤立波的削减能力达到最优，透射系数Ct相较于固定板要减少约20%。当K*=0.5时，相对振幅AR和最大相对速度Vm均取得最大值，二者的变化规律大致相同。不合理的刚度会使升沉板的消浪能力弱于固定板，因此需要正确设计升沉板的支撑刚度。

2) 孤立波通过升沉板时，板会经历一个先上升后下降的运动，在离开升沉板后，升沉板会继续非线性自由振动。板下水流近似均匀流动，其垂向流动与板的垂荡方向一致。升沉板对孤立波的削弱是一个动态平衡的过程，能量通过多种方式耗散，主要涉及到涡旋脱落、浅水变形、波浪反射、波浪破碎和辐射波的生成与转化等现象。

以前的教学活动都是以老师课堂教学为主。翻转课堂实现了课上到课下的翻转。教师在录播教室进行录制，资源可以保存。学生课下通过点播，自主学习教师授课的视频内容，学习灵活主动，实现了课堂翻转。除了录制常规课程，教师还可以录制微课。视频不长，学生注意力更加集中，大大激发学生学习的兴趣。录播教室的投入使用，充分体现了以学生为特色的教学理念。

3) 其他条件相同时，存在一个最佳相对潜深d/h=0.25，使得透射系数Ct得到最小值Ct=0.52，潜深对于升沉板的运动响应基本无影响。

4) 在一定的波高范围，升沉板的消浪性能随着相对波高H/h的增加而增强。与振动幅度相比，升沉板的运动速度对波高的变化更为敏感，线性特征更为明显。

受到所采用数值方法的限制，模型的造波能力有限，在目标波高较大时，造波边界无法造出满足理论要求的孤立波，因此不能准确获得更大范围水深波高比的结果。希望在未来的工作中，能优化数值模型，进一步研究相关内容。