小学数学教学中数形结合思想的融入研究

蔡双治

【摘要】小学数学教学中，数形结合思想的融入有利于简化数学问题，便于学生记忆，还能培养学生学习数学的兴趣.数形结合思想主要用于以形解数、以数助形的解题之中，并通过教师建立生活化数学情境，灵活转换学生思维，巧妙渗透数形结合三种融入途径，降低学生学习数学的困难程度，帮助学生掌握最佳的解题技巧与方法，以此来增强学生的数学思维，提高学生的数学水平，从而促进学生数学解题能力与效率的提升.

【关键词】数形结合思想;数学教学;融入途径

在当前小学数学课程标准的改革下，教学目标已经从关注学生的数学成绩逐渐转变为培养学生的学习能力.可以说，“授人以鱼不如授人以渔”，只要学生掌握适当的学习方法，其数学思维及数学成绩就会有所提升.因此，对于小学数学教学，教师将数形结合思想融入其中，能够有效地减小学生学习数学的难度，使抽象、烦琐的问题简单化，以此来优化学生的数学学习方法，简化数学的答题思维，确保学生的数学水平与解题效率得以提升.

一、小学数学教学中数形结合思想融入的体现

（一）简化数学问题

传统的小学数学教学会出现很多的问题，包括学习困难、枯燥、乏味等等，导致学生无法感受到学习数学的乐趣，难以建立学习数学的信心，以此恶性循环，会使学生陷入无形的苦恼之中.因此，教师在教学中引入数形结合思想，能够清晰地表达出数学问题中数量之间的关系，促使数学学习更加简单，帮助学生形成直观的认识[1].通常情况下数形结合适用于和平面图形有关的题型之中，可以强化学生的数学思维能力，以便学生掌握图形与数量的关系，积累丰富、简单的解题方法，从而轻松地解决数学难题.

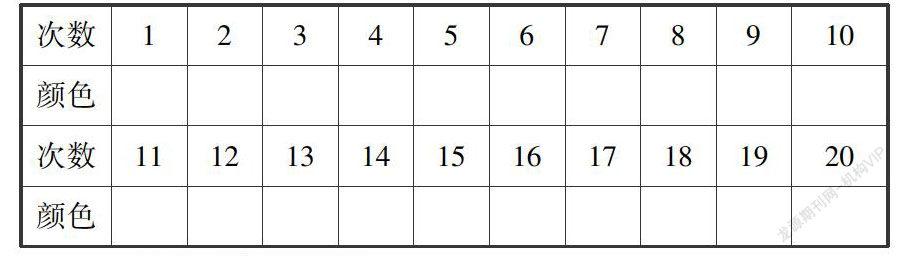
例如，北师大版五年级上册“可能性”一节中的摸球游戏：盒子里有同样大小的红色球和蓝色球，需要摸多少次才能判断出盒子里哪种球多？对于此题，学生就可以借助数形结合思想，摸20次球，同时在下面制作好的表格中记录每次摸球的颜色.学生通过表中的记录很容易就获得答案，降低了学生学习数学的难度.

（二）便于学生记忆

可以说，数学语言始终都是学生头疼的问题，但是图形语言却十分生动，易于学生理解，有利于学生形成形象、长效的记忆[2].因此，教师应在小学数学教学之中融入数形结合思想，采用图形、形状作为分析、研究数学的思维方式，比如一个单一形状的图案可以表达出一个人焦慮或快乐的情绪等.例如笑脸的图标，我们在饭店中经常可以看到笑脸的图标，这是目前市场监督管理局对饭店卫生考核的一个标准，他们通过笑脸的方式让广大的消费者了解该餐厅的卫生及各项指标;相反，如果不是笑脸，就代表卫生不合格.同样如此，在数学学习之中，学生会遇到不同程度的难题，教师画个图形即能够给学生解惑，有助于学生对难题有一个全新的理解和认识，从而有一个深刻的记忆.

（三）培养数学兴趣

教师以几何图形的特点呈现数学问题，使学生能够直观、清晰地理解题意，以此来增强学生对数学问题的直观感受，有利于培养学生对数学学习的兴趣，促使学生感受到学习数学的快乐与成就感，确保小学数学教学质量与效率的有效提升[3].

例如，北师大版五年级下册的“相遇问题”，就可以用数形结合思想直接表达：已知A，B两车同时从甲、乙两地出发，相向而行，A车与B车速度的比为3∶5，两车第一次相遇后，A车速度提高1[]3，B车速度提高1[]2，两车分别到达甲、乙两地后立即返回，第二次相遇点距离第一次相遇点38千米，甲、乙两地相距多少千米？由于这种相遇问题同时涉及了变量及非变量，因此学生对应用题的理解比较局限，此时学生就可以运用数形结合的方式借助图形来理解题意，以此建立起学生学习数学的积极情感，最终实现学生快速、准确地解题，从而使学生对数学学习产生浓厚的兴趣.

二、小学数学教学中数形结合思想主要融入途径

（一）以形解数

通常“形”可以带给学生直观、简单的视觉形式，因此对于小学数学概念性知识，教师就可以运用数形结合思想，以形助数为学生提供基础的数学思维，帮助学生理解数学概念.正因为大部分的数学概念都比较抽象，让学生难懂，即使是五、六年级的学生也无法充分、全面地掌握，所以此时的“形”就能发挥其直观的优势与作用，清楚地展现出数学难题.

例如，北师大版六年级上册“百分数”一课中的“这月我当家”，其主要是让学生会用方程解决有关百分数的简单实际应用问题.因此，数学教师就可以引导学生利用线段图去理解“已知一个数的百分之几是多少，求这个数”的问题，帮助学生体会数学知识之间的联系，同时获得直观、愉快的数学学习体验[4].比如，小明家这月水电支出占总支出的125÷1250=10%，书报支出1250×2%=25元，食品支出500元，求食品支出占总支出的百分比是多少.对于这道题，教师就可以指导学生画线段图理解，将题目中的总支出看作整体“1”，依次用线段表示出各项支出，自然而然地就可以算出总支出.这样一来，“形”就能简单、直观地将一连串的数据展现出来，使抽象的问题简单化，帮助学生从感性认识转化为理性认知，确保学生有方法、有思路、有能力地解决问题.

（二）以数助形

数形结合实质上就是概念与实际的结合，并用数学的两种形式加以表达、描述.虽然“形”可以直观、清晰地显示出数据，但如果遇到粗略的数学问题，就需要“数”来发挥其作用，帮助学生进一步理解与掌握[5].因此，可以说，学生对“形”的深化认识需要“数”的描述与表达.比如线段、射线及直线，现实中线段两端都有端点，射线只有一端有端点，而直线没有端点，所以线段长度无法变化，射线是一端能够伸长、缩短，直线则是两端都能够无限伸长、缩短，这里用“数”的数学语言描述更利于学生建立其相应的形象.

同时，对于几何图形的周长、面积及体积等问题都有特定的数学公式、定理，能够给学生直观的认识.图形面积公式的建立是从数方格开始的，通过一个个地数小正方形的面积，以此来获得其他图形的面积，但要判定图形的性质，就需要通过数学计算得出正确的结论[6].例如，北师大版六年级上册“圆的周长”一课，教师让学生画出周长为20厘米的正方形，学生首先需要通过数学计算求出边长为20÷4=5厘米，然后才能动手画图形.