北斗B1信号干扰快速检测方法研究

刘瑞华，张 硕

（中国民航大学电子信息与自动化学院，天津 300300）

随着卫星数量的增加和频谱资源的使用限制，卫星通信面临复杂的电磁环境。中国北斗卫星导航系统（BDS，Beidou navigation satellite system）的不断完善及其应用使得研究BDS 各工作频段干扰信号的检测分析技术有着重要意义[1]。

干扰信号对北斗B1 信号的精度、可用性、连续性和完好性都构成严重威胁，导致用户定位误差、信号难以捕获等问题[2]。若将北斗B1 信号应用于民航，一旦导航信号受到外来干扰，可能会导致严重事故，甚至造成空难，严重威胁民航安全。因此干扰问题已经成为BDS 应用中不可回避的问题，能够快速检测出干扰信号对民航安全运营有着非常重要的意义。

在卫星导航通信干扰检测中，常见的基于频域的连续均值剔除（CME,consecutive mean excision）算法[3-4]，检测性能较差，为改进CME 算法的不足，文献[5-6]提出了前向连续均值剔除（FCME, forward consecutive mean excision）算法，对所有频域样本的幅值按升序排序，选取幅值较小的部分样本作为无干扰集，再计算初始门限，但此算法中的排序过程大大增加了运算复杂度。

文献[7-8]提出了双门限FCME（DTFCME，dual threshold FCME）算法，设定了两个检测门限，检测性能更好，但包含排序和更多迭代使得运算更为复杂。

为了快速检测出干扰信号，提出一种改进的FCME算法，通过差分算法代替排序算法来寻找初始门限，降低了算法的复杂度，且能有效检测出干扰信号。

1 信号检测模型

1.1 BDS 机载电磁环境分析

将北斗B1 信号应用于民航复杂的电磁环境，其潜在干扰源主要包括：①机载电子设备，如机载甚高频（VHF，very high frequency）通信和高频（HF,high frequency）通信收发机、甚高频全向信标（VOR,VHF omnidirectional radio range）、仪表着陆系统（ILS,instrument landing system）；②固定航空发射机，如VHF 通信、飞机通信寻址与报告系统（ACARS,aircraft communications addressing and reporting system）、测距机（DME, distance measuring equipment）；③邻近飞机干扰源，如VHF通信和DME；④商业无线电，如调幅（AM, amplitude modulation）广播、调频（FM,frequency modulation）广播和电视（TV）VHF 频段、特高频（UHF, ultra high frequency）频段[9]。

对各潜在干扰源进行分析评估，如表1 所示。

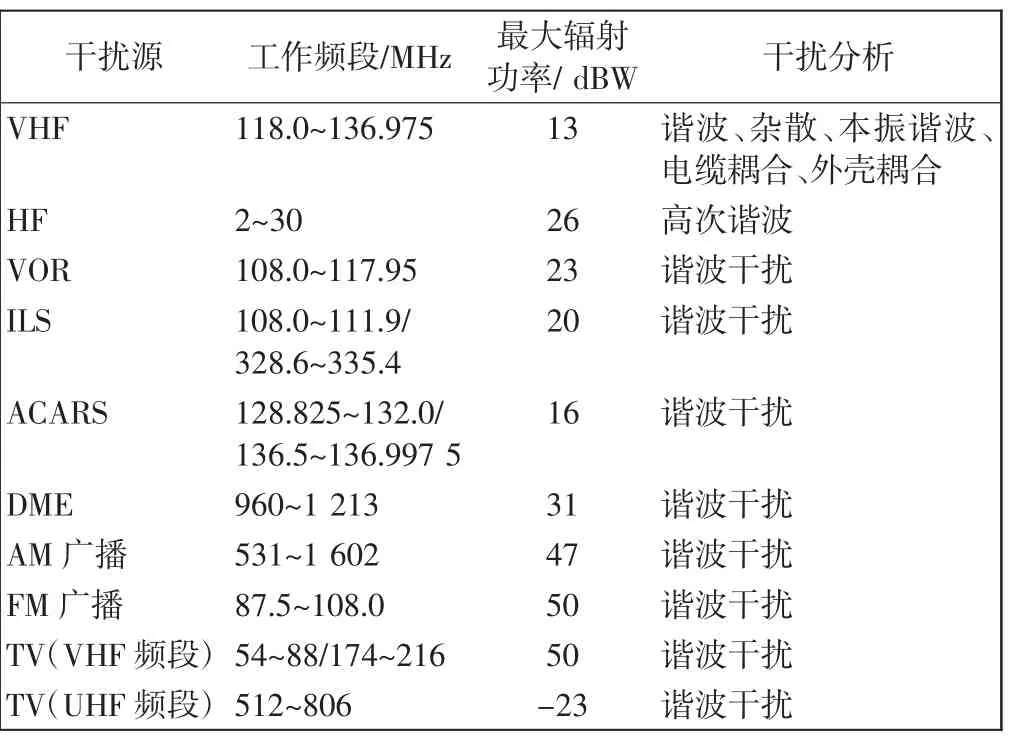
表1 潜在干扰源评估Tab.1 Assessment of potential interference sources

图2 为干扰频点间隔为2.0 MHz 的多音干扰频谱波形，干扰中心频点为1 561.098 MHz，可以看出在多个频点产生连续波冲激。

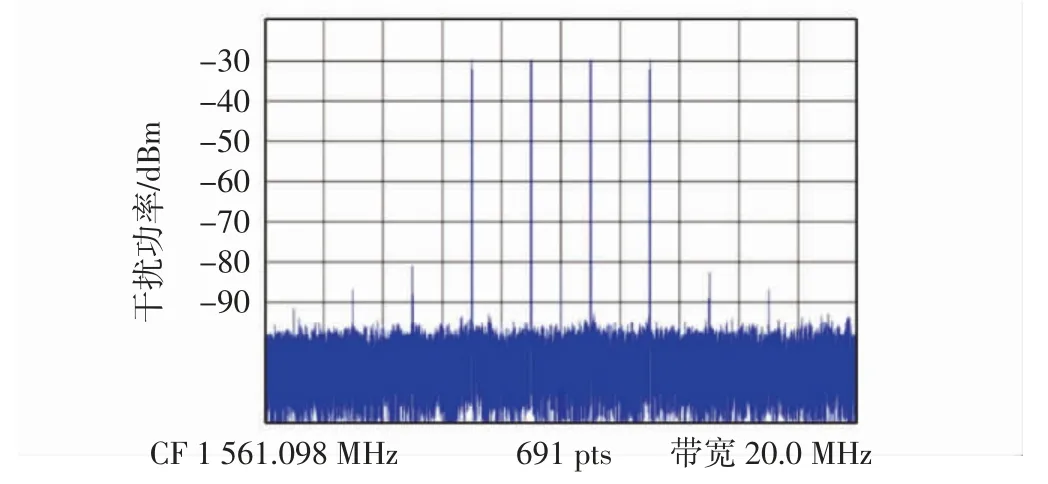
图2 多音干扰频谱Fig.2 Spectrum of comb-spectrum interference

由表1 可看出，尽管频谱的使用有统一规划和严格限制，但由于发射机的非线性效应，其输出的谐波成分很可能会落在有用信号频段内，影响北斗导航接收机的正常工作[10]。

对潜在干扰源进行分析评估，根据其干扰类型进行分类，并与干扰检测结果对比，可缩小干扰源查找范围，有利于对干扰信号源进行快速排查。

1.2 干扰信号

针对北斗B1 信号在传输过程中受到的常见干扰进行分类，对单音干扰、多音干扰、高斯宽带干扰、高斯窄带干扰等几种典型干扰进行建模，并通过频谱仪分析频域特征。

1.2.1 单音干扰

单音干扰又称为连续波干扰（CWI，continuous wave interference），产生的干扰信号可以是一种正弦波信号，在时域连续、频域单个冲激，可表示为

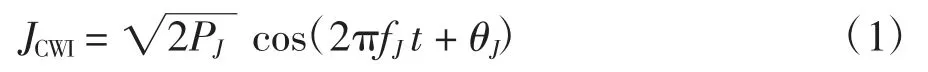
式中：PJ为干扰功率；fJ为干扰信号频率；θJ为随机相位。

图1 为干扰中心频点在1 561.098 MHz 的单音干扰频谱波形，干扰功率为-30 dBm，可以看出在特定的单个频点上产生连续波冲激。

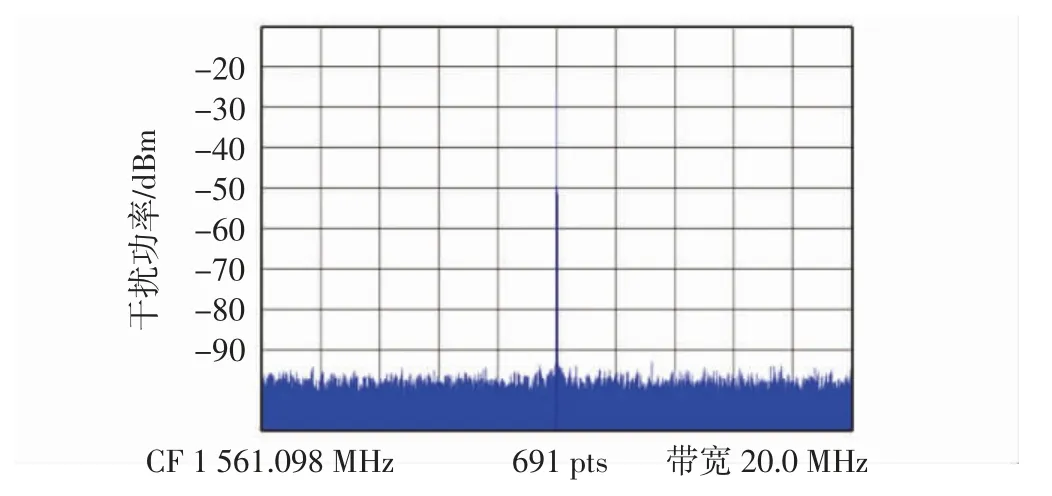
图1 单音干扰频谱Fig.1 Spectrum of continuous wave interference

1.2.2 多音干扰

多音干扰（SCWI, comb-spectrum interference）是将多个单音干扰覆盖在有用信号的信道内，可表示为多个正弦波信号之和，即

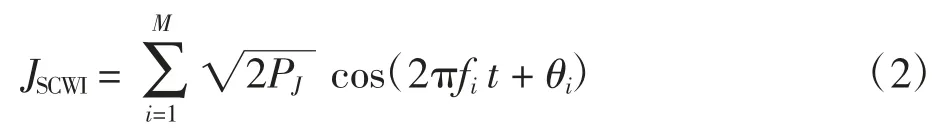
式中：fi为第i 个干扰分量的频率；θi为第i 个干扰分量的随机相位；M 为正弦波信号个数。

1.2.3 高斯宽带干扰

由于接收机前端滤波器的存在，宽带干扰将会覆盖在有用信号带宽内，可使高斯白噪声通过带通滤波器[11]。高斯宽带干扰表示为

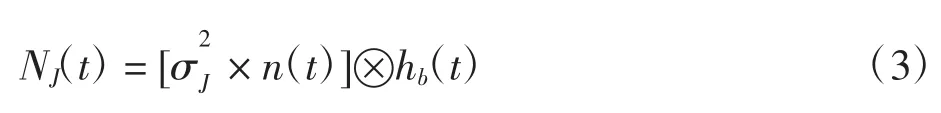
图3 中，设置有用信号频域带宽为2.0 MHz，干扰带宽为500 kHz，干扰中心频点为1 561.098 MHz，可看出高斯宽带干扰频谱带宽超过有用信号带宽的10%。

图3 高斯宽带干扰频谱Fig.3 Interference spectrum of Gauss wideband

1.2.4 高斯窄带干扰

窄带干扰所占频带远小于有用信号带宽（一般不大于有用信号带宽10%），根据不同的产生方式可分为高斯窄带干扰和线性调制窄带干扰[11]。

图4 中，设置有用信号频域带宽为2.0 MHz，干扰带宽为100 kHz，干扰中心频点为1 561.098 MHz，可看出高斯窄带干扰频谱带宽远小于有用信号带宽。

图4 高斯窄带干扰频谱Fig.4 Interference spectrum of Gaussion narrowband

1.3 检测信号

接收机前端的射频信号经下变频到中频信号得到检测信号，由北斗有用信号、高斯白噪声和干扰信号组成，即

式中：s（t）为有用信号；n（t）为高斯白噪声信号；j（t）为干扰信号。

由于卫星信号经过扩频处理后功率很小，淹没在白噪声中，因此，在干扰检测过程中，将其作为噪声信号处理，即成为静默周期检测，检测信号则改为噪声信号和干扰信号组成[12]，即

通过A/D 采样和快速傅里叶变换（FFT，fast Fourier transform）后，接收信号的频域表达式为

式中N 是FFT 变换的长度。FFT 结果为

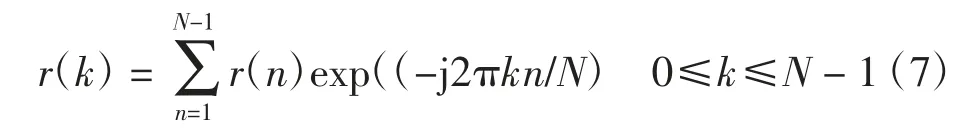
式中r（n）是r（t）的A/D 样本。

2 干扰检测算法

2.1 FCME 算法

频域干扰信号检测的一般假设模型[6]为

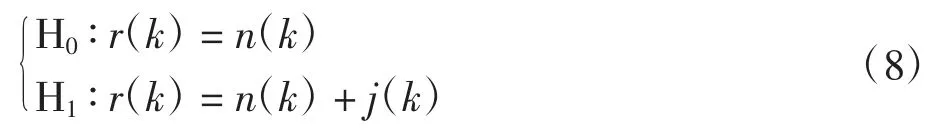
式中：H0中只存在噪声信号；H1中存在噪声信号和干扰信号。

接收信号的频谱谱线幅值为

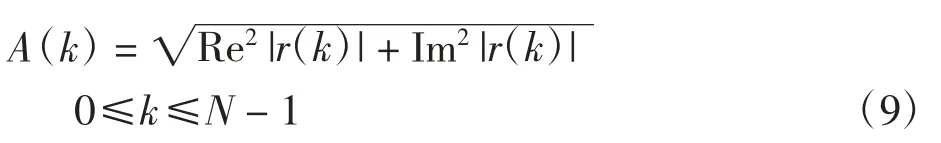
当干扰信号不存在时，接收信号的频谱谱线幅值近似为瑞利分布。根据瑞利分布的特点[3]，接收信号频谱谱线幅值的分布函数和期望可表示为

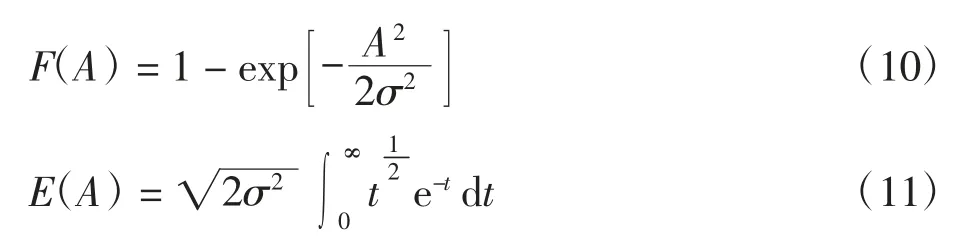
由分布函数可求得

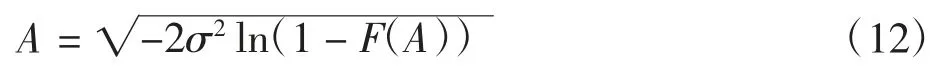
此处，所有样本集合的实际期望值为

假设没有干扰，理论期望值近似等于实际期望值，门限值设为

由此得到干扰检测的门限因子

式中Pf=1-F（AT）为设定的虚警概率，表示样本被错误检测受到干扰的概率。

FCME 算法对CME 算法进行改进，利用连续迭代、逐次逼近的递归方法计算参考门限，用于估计噪声水平，该方法消除了干扰信号的影响，使门限值更接近噪声水平，对干扰信号的检测更准确[6]。

FCME 算法的具体步骤[12]如下。

（1）对接收信号做N 点FFT 运算，并计算频谱谱线幅值A（k）；

（2）根据设定的虚警概率Pf求得干扰检测的门限因子，即

（3）对整个频谱谱线幅值从小到大进行排序，选取其中幅值较小的部分谱线作为噪声频点集，计算出此部分谱线的幅值均值E（A0），由此得到初始干扰门限

（4）将所有频谱谱线幅值与步骤（3）所得门限值进行比较，A（k）＜AT0的频点集合划为无干扰集Im，A（k）≥AT0的频点划为干扰集Jm；

（5）利用无干扰频点集求幅值均值，代替步骤（3）中的均值，计算新的参考门限；

（6）重复步骤（4）、步骤（5）直到没有新的干扰样本点从干扰集中剔除，或者达到最大迭代次数，干扰检测结束。

2.2 改进的FCME 算法

FCME 算法对信号谱线进行排序通常用到性能较好的Quicksort 排序算法[13]，但其复杂度高，不利于快速、实时检测干扰，因此，用差分算法代替排序算法来计算初始门限值。根据FFT 的特点，频谱分布以二分之一采样点中心对称，为了减少计算量，可取一半采样点进行差分算法的干扰检测[14]。

基于频域的干扰检测算法均是通过对信道噪声水平的估计获得最终干扰判决门限[14]，易发现纯噪声频谱相对平坦，噪声频谱的前后差异很小。然而，当接收到的信号有干扰时，频谱谱线幅值会有很大波动，造成干扰频谱与纯噪声频谱的差异很大。因此，当差值很小时，可认为这里很大可能只有噪声信号或干扰信号；当差值较大时，简单判断既有干扰信号又有噪声信号，干扰信号的前半部分或后半部分仅为噪声，从而得到无干扰时信号幅值均值。为了避免干扰旁瓣衰减的影响，将前两段或后两段中差分值最大的两段中较小的一段作为纯噪声段。

差分算法具体步骤如下。

（1）将频谱谱线按顺序划分为q 大小的p 块，并计算每块的幅值均值

（2）计算每两块间的差值

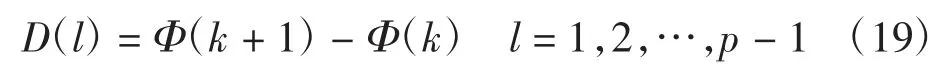
（3）计算D（l）的绝对值，选择差分值的绝对值最大的块L，判断差分值的正负。由于干扰检测信号为噪声信号和干扰信号组成，而噪声信号频谱幅值具有随机性，因此不存在D（L）=0 的情况。如果D（L）＞0，则取L-1 和L-2 块中平均值较小的块作为噪声频点集，且若L=1，则取第1 块的前半部分谱线计算其谱线均值E。如果D（L）＜0，则取L+1 和L+2 块中平均值较小的块作为噪声频点集，且若L=p-1，则取最后1 块的后半部分谱线计算其谱线均值E。最后，取噪声频点集的均值作为噪声级。

（4）初始门限等于上述均值与干扰检测的门限因子的乘积。

差分算法流程图如图5 所示。

图5 差分算法流程图Fig.5 Flowchart of differential algorithm

利用改进的FCME 算法计算初始门限值后，后续迭代流程与FCME 算法相同。

3 仿真分析

3.1 数据处理

北斗B1 信号3 dB 的工作带宽为16 MHz，干扰中心频点为1 561.098 MHz[15]，其受工作带外的干扰影响较小，因此，只考虑带内干扰的影响。北斗B1 信号由中国民航大学建设的卫星导航信号质量分析系统采集得到，采样频率为240 MHz，经一系列转换后的数字中频信号频率为40.258 MHz。

由北斗B1 信号的体制及数字中频信号频率，可将信号3 dB 的工作带宽（32.258 ～48.258 MHz）划分为以40.258 MHz 为中心的7 个频段，并分段进行干扰检测，这样既减少计算量，又可使检测结果更为准确[16]。

北斗B1 信号干扰检测流程具体如图6 所示。

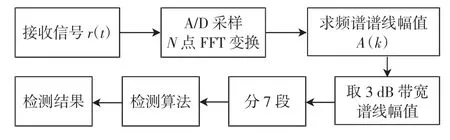
图6 北斗B1 信号干扰检测流程图Fig.6 Flowchart of interference detection on Beidou B1 signal

通过实测信号数据对改进的FCME 算法进行验证。首先，利用矢量信号源模拟产生常见的干扰信号，然后通过采集系统对叠加常见干扰信号的北斗B1 信号进行数据采集，最后对离线数据进行检测分析。

设置检测参数为：采样时间为1 000 ms；虚警概率为1×10-5；FFT 样点数240 000。检测结果如图7 所示，可看出改进的FCME 算法可有效检测出干扰频点，而其他频点为卫星载波泄露和码频泄露现象，不影响卫星信号的接收[16]。

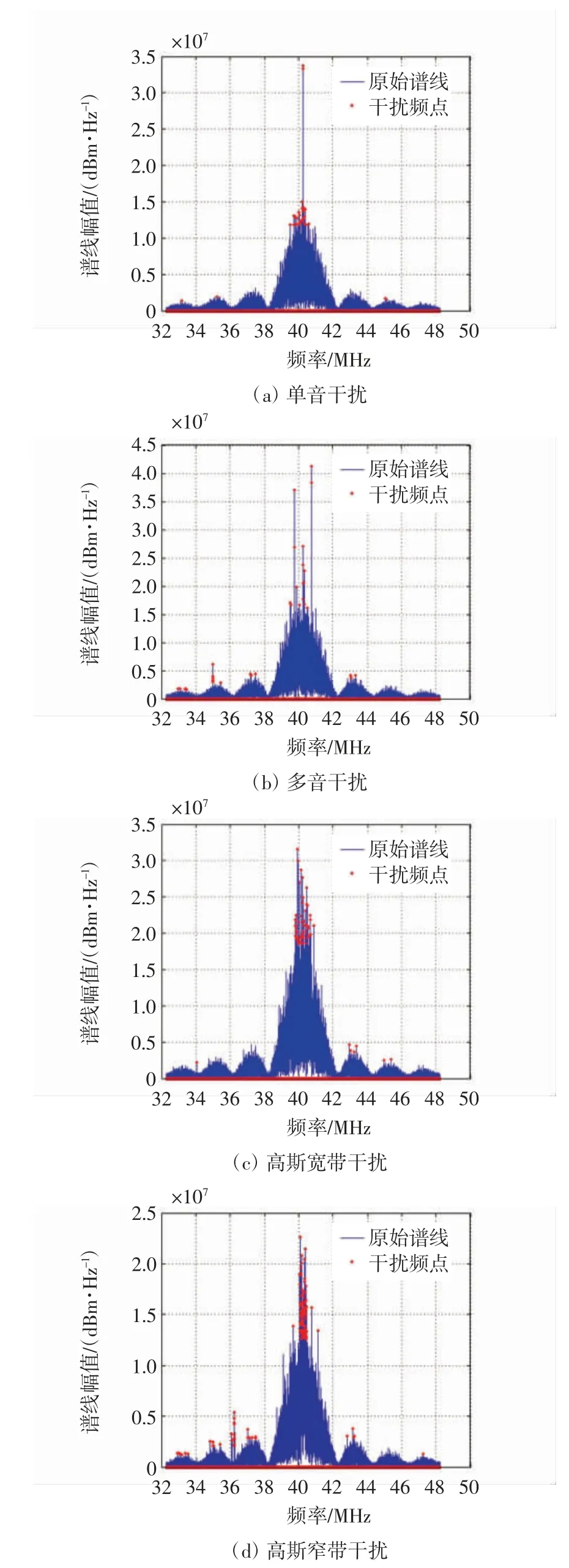
图7 改进的FCME 算法检测结果Fig.7 Detection result of the improved FCME algorithm

3.2 复杂度分析

比较FCME 算法和改进的FCME 算法，由于两种算法的迭代运算是一致的，这里只考虑初始门限计算的复杂性。

假设长度为N 的信号被分成M 段，FCME 使用Quicksort 算法[13]进行排序，时间复杂度为O（Nlog2N），而差分算法时间复杂度为O（N+M+2）。改进的FCME算法中因FFT 运算特点，选取一半频谱点进行干扰检测，将N/2 点重新分成m 块，最后的时间复杂度为O（N/2+m+2），显然，复杂度更低。因此，用差分算法代替FCME 中的排序算法，降低了运算复杂度。

3.3 检测性能分析

为了比较改进的FCME 算法与传统CME[4]、FCME[6]和DTFCME[8]算法的性能，在不同干噪比下，对干扰信号进行蒙特卡洛检测性能仿真。其中，干噪比为干扰信号功率与噪声功率的比值，干噪比越大，表明所受干扰信号功率越强。

设置仿真参数为：蒙特卡洛仿真次数为1 000；干噪比为-30～30 dB，步进为1 dB；FFT 点数N=1 000；FCME算法虚警概率为1×10-5；DTFCME 算法高、低虚警概率为1×10-5、5×10-3；差分算法分块数为20。

干扰信号类型为CWI、SCWI 和线性扫频干扰（LFM，linear frequency modulation interference）时，不同算法干扰检测性能对比如图8 所示，可看出4 种算法的模拟检测概率几乎相同。对于CWI，当干噪比为-10 dB 时，均可检测出干扰信号，检测概率为1；对于SCWI，当干噪比为-12 dB 时，均可检测出干扰信号，检测概率为1；对于有一定带宽的LFM，当干噪比为10 dB 左右时，均可检测出干扰信号，检测概率为1，但对LFM 信号检测性能较差。

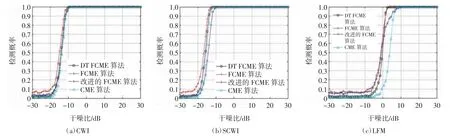
图8 不同算法在多种干扰信号类型下的检测性能对比Fig.8 Comparison of detection performance among different algorithms under various interference singnals

综上，当干扰信号的功率大大低于噪声功率时，干扰已融入背景噪声，几乎无法有效检测。随着干扰带宽的增加，干扰次数增多，导致能量的分散、检测性能降低，要达到相同的检测概率，则需要更大的干噪比。此外，改进的FCME 算法大大降低了算法的复杂度，而由于多径效应的影响，接收信号的噪声底限波动很大，导致检测性能降低。

4 结语

为保证北斗B1 信号在民航中更好地应用，对北斗B1 信号干扰进行快速检测。为了降低传统FCME算法的运算复杂度，利用差分算法计算初始检测门限，提出了改进的FCME 算法，并通过实测信号验证了其有效性。仿真分析结果表明，该算法的性能优于CME，与FCME 和DTFCME 相似，均可有效检测出干扰信号。