形状记忆合金驱动可变形机翼的设计优化

刘兵飞，张 超，张 威

（中国民航大学航空工程学院，天津 300300）

现代飞行器所面临的飞行条件及任务要求越来越苛刻，但常规方法[1]设计的机翼仅在特定飞行状态下具有良好的气动性能。为使其气动性能在整个飞行过程中保持最优，可变形机翼的设计应运而生，其可根据不同飞行状态自动调整机翼形状，从而获得较优的气动性能[2-3]。

当前可变形机翼的研究重点多为改变机翼前、后缘形状。典型的应用包括前缘和后缘装置的驱动[4]以及小规模的表面偏转，以增加特定飞行条件下的气动性能[5]。然而，该变形方式在面对特定飞行条件时仍存在很多问题[6-7]。因为机翼整体为刚性状态，不能根据飞行状态的改变及时调整机翼形状进而改善气动性能。且当前一般采用液压机械系统作为驱动机构，该机构结构复杂、质量较重、占用空间较大，在一定程度上抵消了因机翼变形而获得的性能提升。因此，须选择新型智能材料为代表的驱动器作为可变形机翼的驱动机构。目前对形状记忆合金的研究表明，形状记忆合金（SMA,shape memory alloy）材料具有独特的形状记忆效应和超弹性，可用作快速响应、轻型、大应力的驱动器，适用于可变形机翼[8-10]。

国内外学者基于Isight 平台，通过CFD 软件对翼型自主优化理论与设计进行了大量研究[11-14]，以展示对机翼进行建模仿真及优化设计的可行性。基于此，以NACA 0012 初始翼型为例，设计SMA 丝驱动的可变形机翼结构，将SMA 驱动器上下驱动点连接到翼型内侧桁条上，通过SMA 丝变形驱动桁条上下移动带动柔性蒙皮变形。然后在Isight 平台进行机翼建模和流体力学分析，并对机翼的升力系数、阻力系数以及升阻比进行数值计算和分析，从而获得不同飞行状态下气动性能最优的机翼形状。最后基于优化结果确定机翼变形程度与SMA 丝变形量之间的关系，结合SMA本构理论，通过力-热-应变耦合方法，确定满足变形条件的可变形机翼结构方案。

1 可变形机翼驱动结构设计

可变形机翼驱动结构主要包括驱动器、控制器、传感器以及驱动平台等。驱动平台基于NACA 0012 翼型，如图1 所示，机翼平面尺寸为1 000 mm×1 000 mm，即弦长C=1 000 mm，展长W=1 000 mm，展向长度D=750 mm，翼型最大厚度为120 mm，翼梁长度为980 mm，用于将两个翼肋连接起来，每个翼肋的厚度为10 mm。两翼肋垂直对称且平行设置，每个翼肋的内侧面中部沿垂直方向设有一道凹槽。两桁条上下平行设置，两端分别向外形成一个能够插入翼肋上凹槽的凸台，使桁条能够沿凹槽上下移动。柔性蒙皮覆盖在翼梁、前墙和后墙的上下端外部，内表面与桁条外表面相连接。如图1 所示。

图1 驱动平台Fig.1 Drive platform

为实现单一方向变形，考虑控制复杂度，选择偏动式[15]SMA 驱动方案，该驱动器体积较小、控制简单、位移较大，不影响正常飞行，且可利用通断电、加热冷却来进行驱动。SMA 驱动器外部尺寸参数如图2 所示。SMA 驱动器内弦向长度E=300 mm，

图2 阴影部分假设为刚性结构，上表面的可变形柔性蒙皮位于机翼整体弦长的3%～80%、2%～85%处。假设可变形蒙皮与刚性结构可平滑过渡。

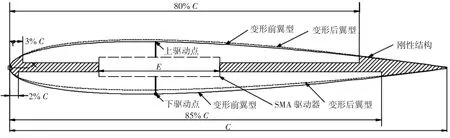
图2 驱动设计平台参数Fig.2 Parameters of driver design platform

SMA 驱动器结构如图3 所示，为实现机翼变形，首先将SMA 驱动器沿翼展方向固定在如图1 所示的翼梁上。根据机翼变形方向，设计位移转换机构，将SMA 驱动器产生的水平方向位移转化为竖直方向位移。机构转换比（水平方向位移与竖直方向位移之比）越大，驱动材料SMA 丝应变量也越大，即要求SMA 丝的初始长度L 越长。考虑机翼内空间有限，需对SMA丝的长度进行合理控制。

图3 驱动器结构图Fig.3 Diagram of driver structure

采用通电方式对SMA 驱动器进行温度控制。首先，将电阻丝缠绕于SMA 丝表面，将其覆盖；然后，在最外层包裹弹性绝缘蒙皮，使其在飞行过程中不受外界环境影响。对SMA 驱动器进行通断电，以实现翼型控制：通电加热后，SMA 丝产生回复力，克服弹簧弹力，拉动转换机构向右移动；转换机构在运动过程中将水平位移转换为竖直位移施加到桁条上，桁条驱动蒙皮发生变形，从而改变机翼形状；停止加热，SMA 丝产生的拉力变小，弹簧弹力推动整个结构返回原位，机翼恢复原样。

2 可变形机翼的优化设计

选用初始翼型NACA 0012 作为优化算例，采用基于Isight 平台的非支配解排序遗传算法进行优化，设计要求如下：

（1）自由来流速度为50 m/s，迎角为5°，Fluent 计算采用Spalart-Allmaras 模型；

（2）提高升力系数cl，降低阻力系数cd，提高升阻比p。

基于Isight 平台的翼型集成优化流程如图4 所示。

图4 翼型集成优化流程Fig.4 Integrated airfoil optimization process

在集成优化设计过程中，通过调整控制翼型生成的参数来自动生成新的翼型数据，因此，需对初始翼型数据进行参数化定义。传统的翼型参数化方法包括多项式拟合法[16]和解析函数线性叠加法等[17]，其中，多项式拟合方法对翼型局部的微调效果欠佳，其各项系数对翼型形状的影响不均衡[18]。因此，利用解析函数线性叠加法对翼型进行参数化定义，翼型形状可表示为初始翼型和扰动的线性组合[19]，即

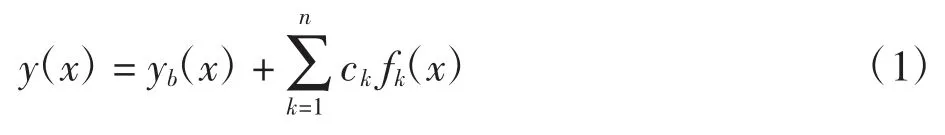
式中：x 为初始翼型弦长，规定范围为0～1；y（x）为优化后翼型形状；yb（x）为初始翼型的形状；k 为翼型厚度相关控制点的变量个数；ck为翼型形状调控相关的系数；fk（x）为型函数，即

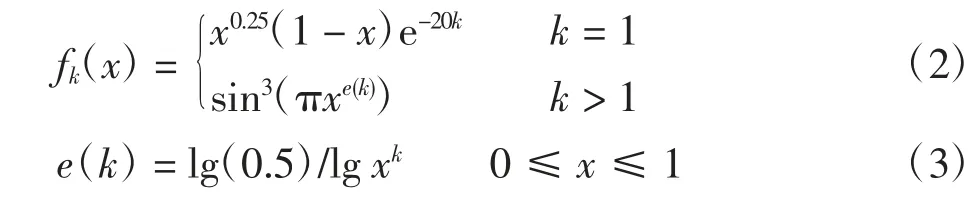
在翼型函数中引入变量个数k，以控制翼型形形状的改变。xk（k=2、3、4、5、6、7）分别取0.15、0.30、0.45、0.60、0.75、0.90。结合初始翼型和设计变量ck来确定优化后的翼型形状。14 个变量取值范围规定在-0.01～0.01之间[20]。利用Matlab 进行编程，得到优化后的翼型参数。然后，将翼型参数导入Ansys 的网格划分工具Icem 模块，自动进行网格划分，翼型附近网格如图5所示。

图5 翼型附近网格Fig.5 Grid near airfoil

然后采用Ansys 的Fluent 模块进行气动性能分析，得到翼型气动性能分析结果，最后根据优化目标，进行自动“循坏”计算，从而得到最优的翼型数据。其中，初始翼型和优化后翼型的气动性能比较如表1 所示。

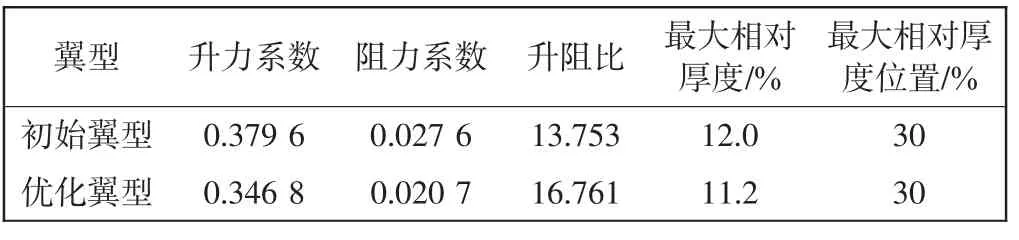
表1 初始翼型和优化翼型气动性能对比Tab.1 Comparison of aerodynamic performance between original and optimized airfoils

从表1 可以得出，相对于升力系数，优化后翼型的阻力系数降低更为明显，优化翼型升阻比提高了大约21.87%。最大相对厚度由初始的12.0%变为优化后的11.2%，最大相对厚度位置仍为30%弦长处。

已知设计平台NACA0012翼型平面尺寸为1 000 mm×1 000 mm，即展长W 和弦长C 均为1 000 mm。基于此，优化后翼型最大厚度由初始的120 mm 变为优化后的112 mm，即变形目标是在最大厚度为120 mm 的翼型上实现0～8 mm 的变形，优化翼型如图6 虚线所示。

从图6 可以看出，翼型上下表面分别实现了0～2 mm、0～6 mm 的变形。优化后翼型不再上下对称，上表面前缘部分稍微降低，前缘半径略微减小，有效降低了阻力；上表面中部略微抬高，且上表面后缘略微下降，下表面中间部分明显抬高，翼型下表面更加平坦，这也有利于减小阻力。优化前后翼型压力系数分布如图7 所示。

图6 初始翼型和优化翼型Fig.6 Initial airfoil and optimized airfoil

图7 优化前后翼型压力系数分布Fig.7 Pressure coefficient distribution of airfoil before and after optimization

从图7 可以看出，优化后翼型上下表面压力系数均有一定下移，但上表面的下移更多，导致翼型中部压力系数收缩，升力系数降低。综上所述，虽然优化翼型升力有所降低，但阻力下降幅度更大，从而使得升阻比明显上升，达到优化目的。

3 可变形机翼结构的实现

为实现机翼变形目标，假设上下驱动点连接在翼型最大厚度处。其中，设置上驱动点驱动机构的转换比为9 ∶1，即驱动机构SMA 丝水平位移为0～18 mm时，上表面柔性蒙皮最大厚度点可实现0～2 mm 的竖直位移。同理，设置下驱动点驱动机构的转换比为3 ∶1，即驱动机构SMA 丝水平位移为0～18 mm 时，下表面柔性蒙皮最大厚度点可实现0～6 mm 的竖直位移。基于以上优化设计结果，结合SMA 本构关系，通过热力耦合方法确定满足优化设计要求的可变形机翼驱动结构方案。

3.1 SMA 本构关系

令选取的SMA 材料模型仅受轴向拉力，并且该模型沿轴向尺寸比径向尺寸大很多，所以，仅考虑轴向变形。对于一维情况，可最终得出SMA 的本构关系[21]为

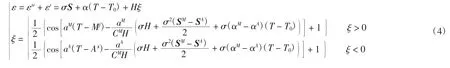
式中：T 为温度；T0为参考状态下的温度；σ 为应力；SM为马氏体柔度张量；SA为奥氏体柔度张量；As为奥氏体相变开始温度；Mf为马氏体相变完成温度；αA和αM分别为奥氏体相和马氏体相热膨胀系数；H 为最大相变应变；CM为马氏体应力影响系数。

3.2 数值计算

模拟SMA 材料特性总结[22]如表2 所示，以便对SMA的温度-应变关系进行数值计算。

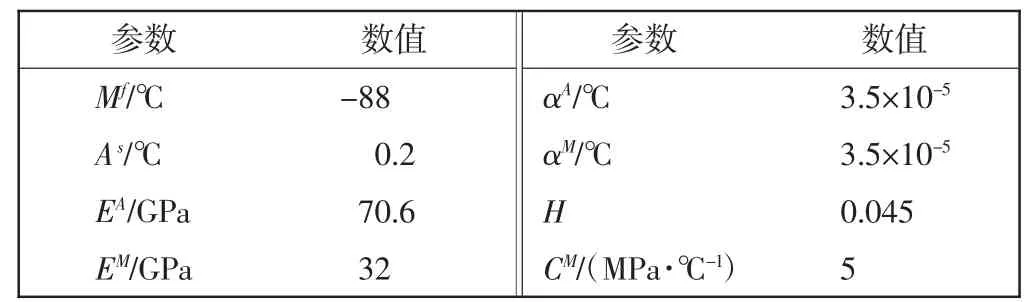
表2 SMA 材料属性Tab.2 Properties of SMA material

其中EA和EM分别为奥氏体和马氏体杨氏模量；分别在400、500、600、700 MPa 的预应力作用及-50 ℃～200 ℃的热循环条件下，对SMA 丝的温度应变关系进行计算，数值结果如图8 所示。随着应力的增大，通过控制温度可以实现SMA 丝的应变也逐渐变大。不同应力下SMA 丝的温度控制区间及可实现的应变如表3 所示。

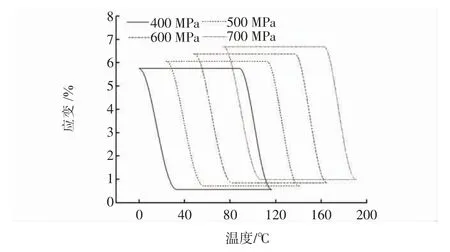
图8 不同应力作用下的温度-应变曲线Fig.8 Temperature-strain curve under different stresses

由表3 可知，SMA 丝应变量随应力增加而逐渐增大，基于结构设计，原则上应变量越大越好。用户可根据不同温度要求进行自主设计，以500 MPa 应力下为例，温度范围应控制为30～140 ℃。计算得到驱动器SMA 丝位移量为18 mm 的目标下，该结构设计所需SMA 丝长度L=334 mm。

表3 SMA 丝温度控制区间及可实现应变Tab.3 Temperature control interval and achievable strain of SMA wire

通过转换机构，将水平位移转化为竖直位移，最终实现基于SMA 丝驱动可变形机翼结构的设计。

4 结语

（1）优化方案可将翼型升阻比提高约21.87%。

（2）为简化变形机翼模型，将SMA 驱动器上下驱动点直接布置在翼型最大厚度位置处，不能保证其他翼型位置点也恰好达到指定位置，难以准确实现优化后的翼型。

后续研究将结合热力耦合结构分析与流体力学气动分析，形成适应性评估函数，利用该函数通过混合遗传算法来确定SMA 驱动器的最佳布置位置，从而使翼型在特定飞行条件下准确变为优化后的形状，达到最优的气动性能。