大地电磁场源效应特征分析及其校正研究

罗威， 王绪本 ， 王堃鹏， 张刚， 李德伟， 杨钰菡

1 地球勘探与信息技术教育部重点实验室(成都理工大学)， 成都 610059 2 四川省冶勘设计集团有限公司， 成都 610084 3 西南科技大学环境与资源学院， 四川绵阳 621010

0 引言

大地电磁测深是探测地球深部电性结构的主要方法，通过在地表同步观测电场、磁场分量，定性或定量地分析获取地球一定深度范围内的电性结构模型，在油气勘探、固体矿产资源勘察、深部地质结构探测、地热和地下水资源调查、地震预测和地质灾害防治等领域应用广泛.

关于大地电磁场源问题，最早Cagniard(1953)提出大地电磁测深法时将场源假设为理想的平面电磁波，但实际的场源形式较为复杂，因此诸多研究者对平面波假设产生了质疑，指出大地电磁仍然可能存在场源效应，即非平面波场影响.Wait(1954)提出，如果电磁波场的横向均匀范围并不远大于其趋肤深度，那么Cagniard所提出的大地电磁理论公式将不能成立，须引入相应的校正项.Price(1962)引入了场源的影响项ν(2π/ν表示场源横向波长)，并给出了ν的取值范围一般在1.57×10-4～1.57×10-2km-1.Madden和Nelson(1986)研究认为平面波的假设普遍适用于中纬度地区、周期数千秒内的大地电磁测深，其余情况则未必可靠.Srivastava(1965)模拟了横向波动的波数场场源，认为场源效应在约千秒周期后开始显现，且总体上相位比视电阻率的场源效应更严重.Hermance和Peltier(1970)采用线电流源研究了均匀和层状大地模型的场源效应，高文(1991)在其基础上进一步对线电流源分析了电阻率、周期对场源效应的混合影响.Peltier和Hermance(1971)又认为他们之前对线电流源模型过于简化，难以模拟实际中的场源分布，指出真实的大地电磁场源可能在横向上存在高斯分布，采用高斯电流源模拟了大地电磁响应.总结这些已有研究，主要指出在高频情况下大地电磁的平面波场源假设是合理的，但在低频情况下平面波的假设就未必可靠，即大地电磁在一定情况下也可能会受到场源效应影响.

在了解到大地电磁可能存在场源效应影响后，少量学者开展了关于大地电磁场源效应的校正研究.高文(1991)在模拟计算高空线电流源时，提出了一种“测点平均法”，从理论上指出有一定效果，但并未做模拟证明.Lezaeta等(2007)对加拿大北部极圈内1998—2000年长期观测的大地电磁资料做了处理分析，发现延长数据观测时间对降低场源效应有一定作用.Jones和Spratt(2002)研究场源效应时发现场源效应的强弱与垂直磁场分量密切相关，提出了一种时间域剔除法校正场源效应.

由于我们所处的地球表面电磁环境异常复杂，大地电磁的天然场源在不同时段、不同区域可能是由平面波源与多种非平面波源共同组合作用，在诸多情况下很可能具有显著的场源效应特征.比如测点位置靠近极光带，极光电集流一般具有明显的条状或带状特征，此时在某些频段或位置的平面电磁波假设很可能不再合理.另外，在靠近赤道区域存在赤道环电流，在中纬度地区也可能存在横向波动的波数场，在这些很可能不满足平面波场的区域或相应频段，目前对大地电磁效应特征以及如何对其进行校正的认识都比较局限.

因此，针对大地电磁场源效应问题，本文将采用多种模型开展线电流源、片电流源和波数场源三种典型非平面波场源的正演模拟，分析大地电磁场源效应特征，指出电阻率、频率、测点位置和源参数对场源效应的影响情况.对于大地电磁场源效应的校正问题，本文将归纳和试验几种校正方法，并提出两种新的场源效应校正方法.

1 线电流源大地电磁场源效应

1.1 线电流源一维正演

在靠近极圈的高纬度区域普遍存在极光电集流体系，在靠近赤道的低纬度区域上空存在赤道环电流，这些场源具有明显的线状特征，可先将其假设为相对简单的线电流源(Hermance and Peltier，1970)开展大地电磁一维正演模拟.

图1 线电流源-层状介质模型示意图Fig.1 Line current source-layered model

线电流源的场源假设和模型示意如图1所示.由于极光电集流和赤道环电流一般均是沿纬度方向，因此在直角坐标系中定义为x向北、y向东、z向下，无限长的线电流源平行于y轴位于z=-h的上空，z=0为地表.根据Hermance和Peltier(1970)的推导，无限长线电流源在地表不同x位置的电场和磁场分量可表示为关于波数v的正余弦积分：

(1)

(2)

(3)

式中的R为关于地下电性结构的地面反射系数：

(4)

其中Z为平面电磁波场源在层状介质地表的阻抗响应，Z=-Ey/Hx，Bx=μ0Hx.

(5)

(6)

(7)

在求得线电流源地表电磁场响应后，为便于分析对比场源效应特征，这里采用与平面波一样的卡尼亚阻抗来定义线源在地表的视电阻率和阻抗相位公式：

(8)

(9)

1.2 线电流源场源效应模型分析

在求得线电流源地表电磁场响应后，下面通过对不同场源参数和不同地电模型进行模拟，分析线电流源的场源效应.

(1)均匀半空间模型线源正演响应

根据极光电集流的一般情况，这里假设线电流源高度100 km，电流100万安培，模型为电阻率100 Ωm均匀半空间，地表测点间距100 km，测点从线源开始至最远距离10000 km处，计算频率从102～10-5Hz，图2中不同颜色代表几种频率的正演视电阻率和相位曲线，横坐标为测点位置，纵坐标分别为视电阻率和相位值.对于平面波场源，其均匀半空间模型的正演响应应当是均一值，而线源正演结果表明，在测点位置靠近线源处视电阻率和相位曲线均波动较大，与平面波源计算结果差异大，且频率越低差异越明显，表明线源在“近区”的场源效应较强.当测点位置远离线源时，视电阻率和相位曲线均逐渐靠近平面波正演结果，表明线源在“远区”的波场是接近于平面波的，场源效应相对较弱.

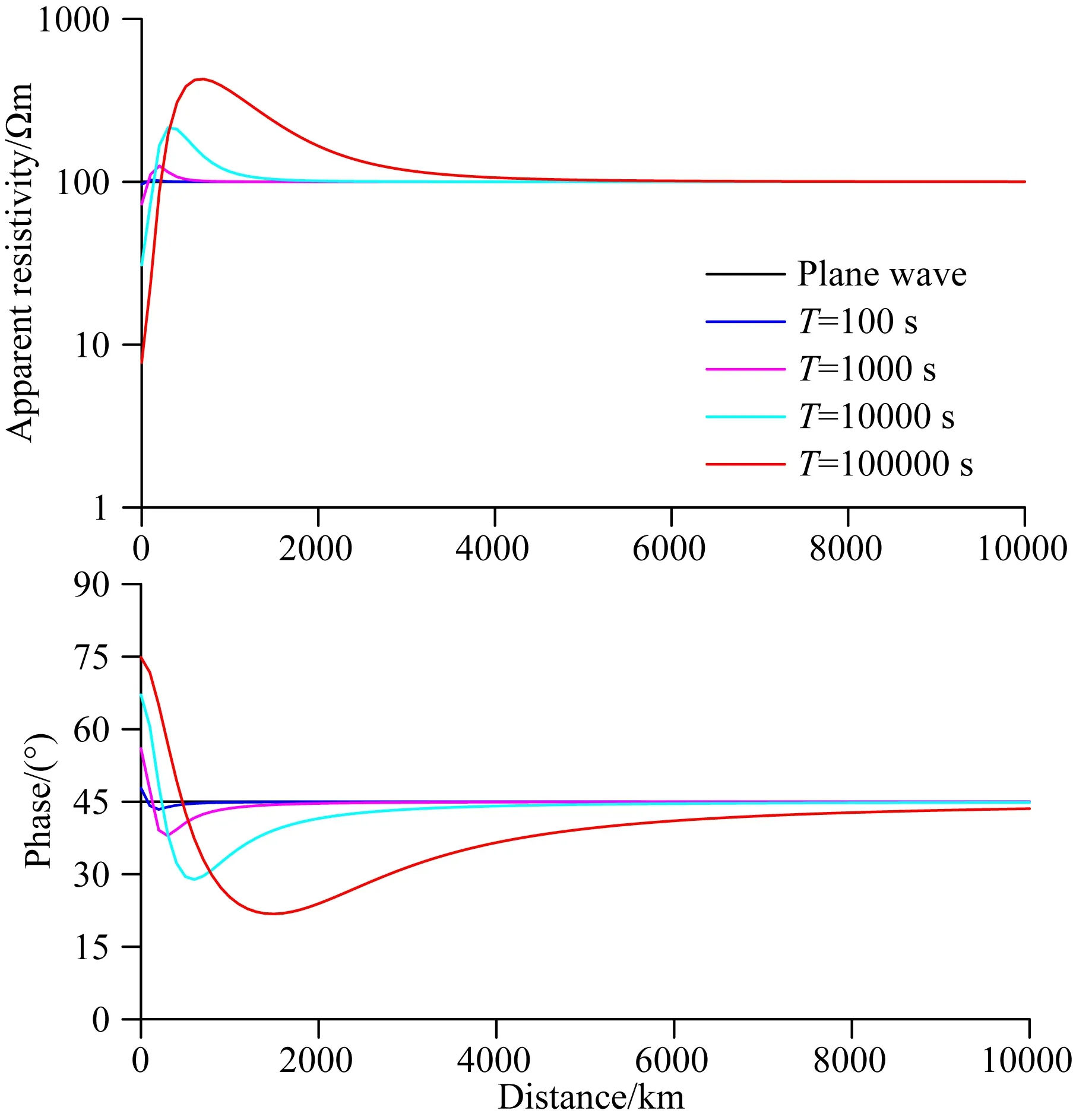
图2 均匀半空间模型线电流源正演响应Fig.2 Response of line current source in uniform half-space model

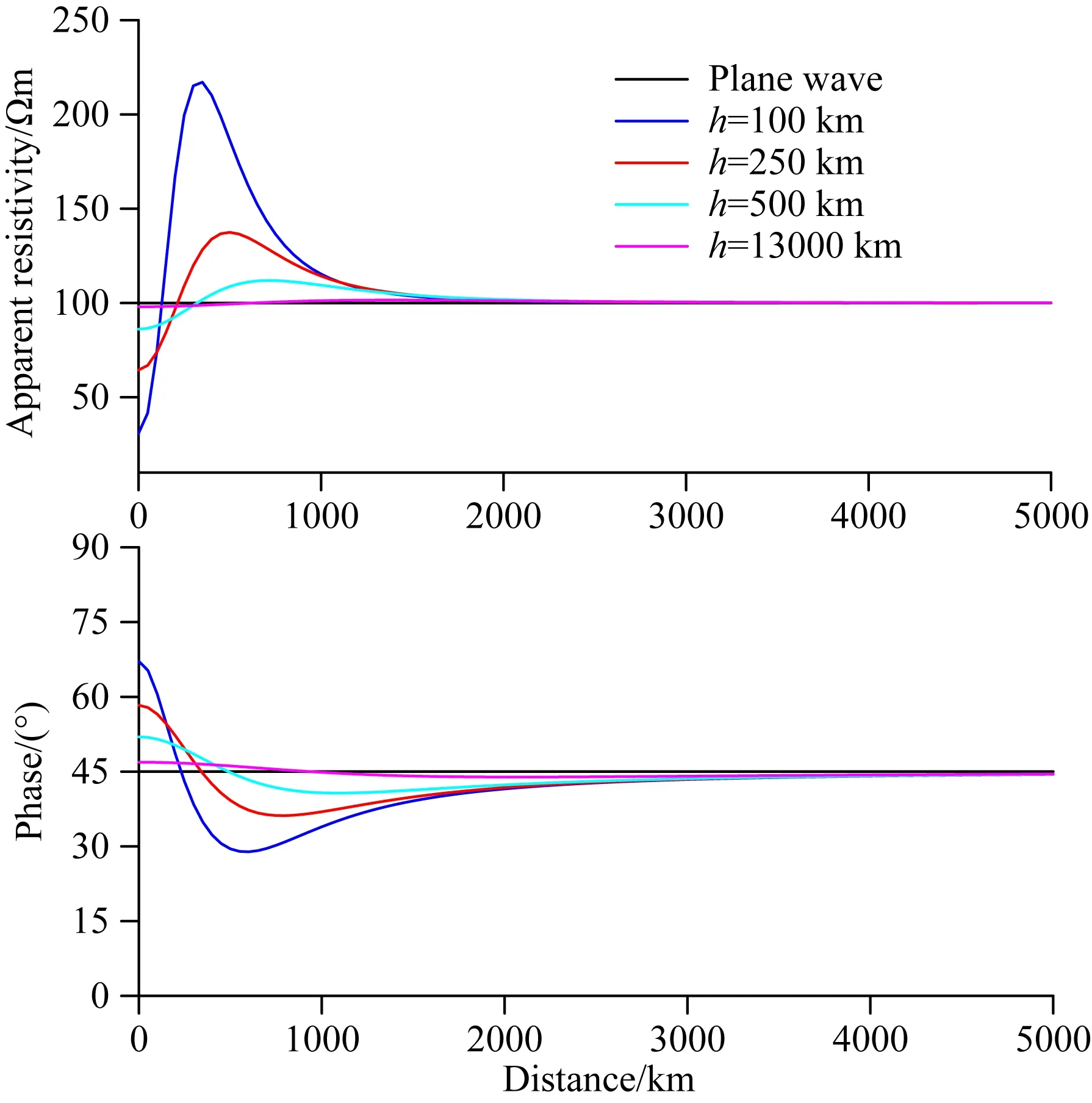
图3 不同高度线电流源的正演响应Fig.3 Responses of different heights line current sources

(2)不同高度线源的正演响应

典型的非平面波场源类型有极光电集流和赤道环电流，其中大多数极光电集流出现在地球上空90～130 km处，最高可达数千千米，赤道环电流位于距地心约2～10倍地球半径范围.因此，有必要对不同高度情况下线电流源在地表的电磁响应特征开展模拟分析.这里假设线电流源电流100万安培，均匀半空间电阻率100 Ωm，地表测点间距50 km，测点从线源开始至最远距离5000 km处，计算周期T=10000 s时线源高度分别为100 km、250 km、500 km、13000 km的响应.图3为100 Ωm模型正演结果，横坐标为测点位置，纵坐标为视电阻率和相位，图中不同颜色的曲线分别代表几种线源高度的响应结果.可以看出，在靠近场源区，不同高度的线源响应波动幅度不同，线源高度越小波动峰值越大，线源高度越大越趋于平面波响应，其中100 km、250 km、500 km可模拟极光区，场源效应较为明显，13000 km可模拟赤道区域，场源效应相对较弱.

(3)稳定区域模型线源正演响应

根据Keller(1971)对整个地球壳幔电性结构特征的概括，地壳和上地幔的电性分布可主要分为构造活动区域和稳定地台区域.在不同构造单元的上地幔高导层埋深不同，构造活动区域的上地幔高导层埋深较浅，一般约为几十公里，而稳定地台区域的上地幔高导层埋深较大，较深处可达数百公里.因此建立类似的地电模型开展模拟分析，能一定程度了解线电源的实际影响程度.这里参考Hermance和Peltier(1970)对稳定地台区域电性模型假设，模型可简单假设为两层结构，表层为厚100 km、电阻率10000 Ωm的较厚高阻地壳层，其下为100 Ωm的上地幔层，模型如图4所示.

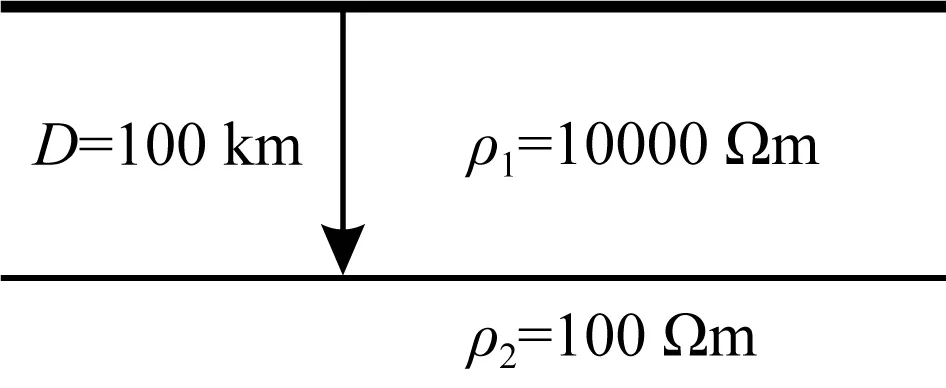
图4 稳定区域模型Fig.4 Stable region model

假设线电流源电流100万安培，高度100 km，以线源为中心，左右分布各5000 km，计算频率102～10-5Hz.另外，为了比较模型线源和平面波源的响应差异情况，这里同时计算了平面波场的响应以及两种源响应的相对误差值.图5为稳定地台区域模型正演结果，横坐标为测点位置，纵坐标为频率.与均匀半空间模型一样，稳定地台区域模型的线源响应与平面波源响应断面相比，在高频段和测点远离源的区域基本一致，在低频段或靠近线源区域差异显著.从两种源的相对误差断面图更能直观的看出计算差异的数值和区域，其中视电阻率的最大相对误差达到了327%，相位的最大误差达到了56%，表明稳定地台区域模型在一定区域或频段场源效应较为严重.这里以相对误差10%为尺度进行评估，选取与线源水平距离分别为50 km、1000 km、3000 km和5000 km四个不同测点，其视电阻率差异超过10%的周期分别约为6 s、1500 s、40000 s、>100000 s，相位差异超过10%的周期分别约为1000 s、4000 s、32000 s、70000 s.

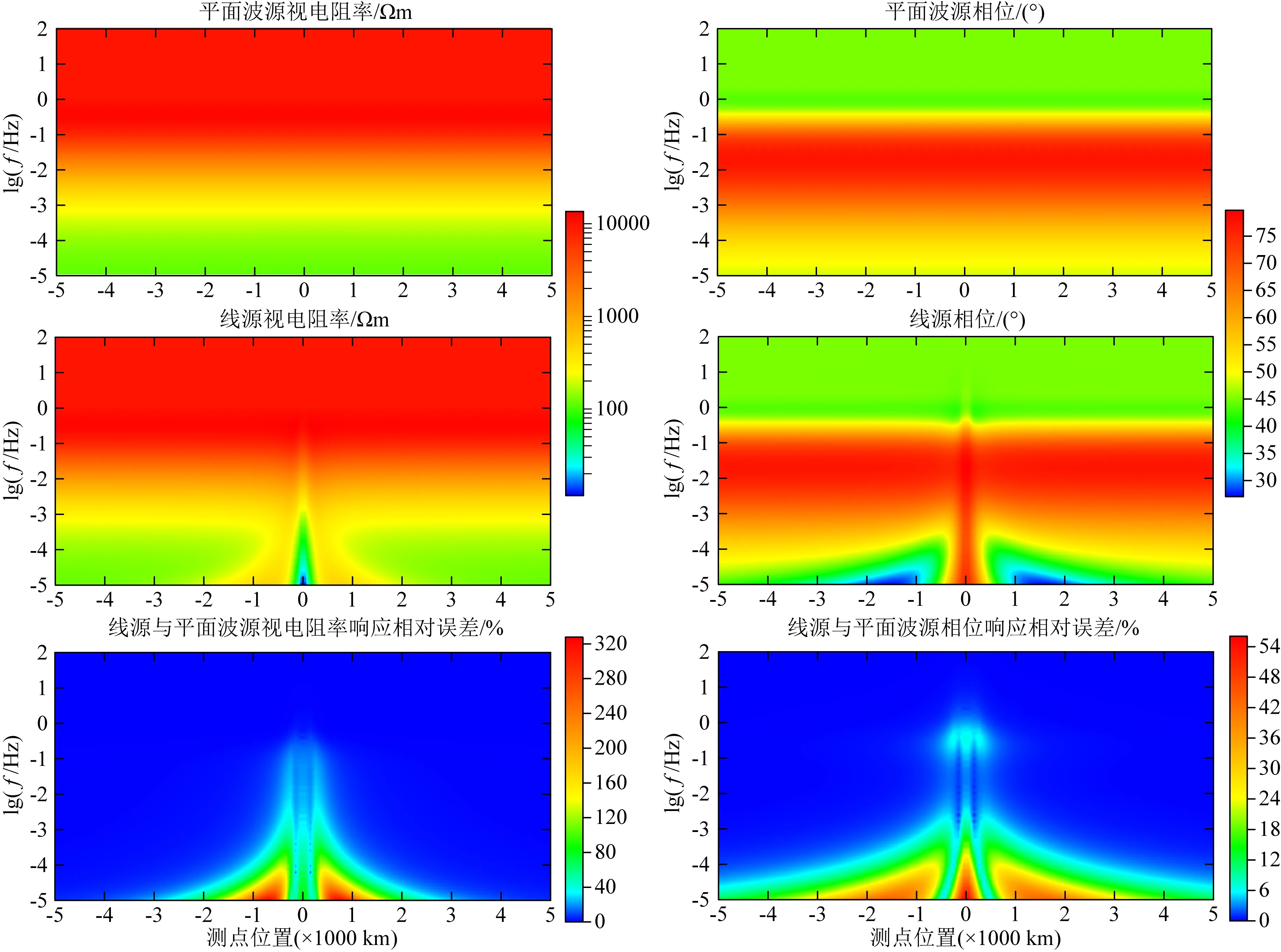
图5 稳定区域模型线源与平面波源正演响应及其相对误差Fig.5 Response and relative error between line source and plane wave source in stable region model

(4)活动区域模型线源正演响应

同样参考Hermance和Peltier(1970)对构造活动区域的电性模型假设，模型可简单假设为图6所示两层模型，表层为厚25 km、电阻率1000 Ωm的较薄地壳层，其下为10 Ωm的上地幔层.

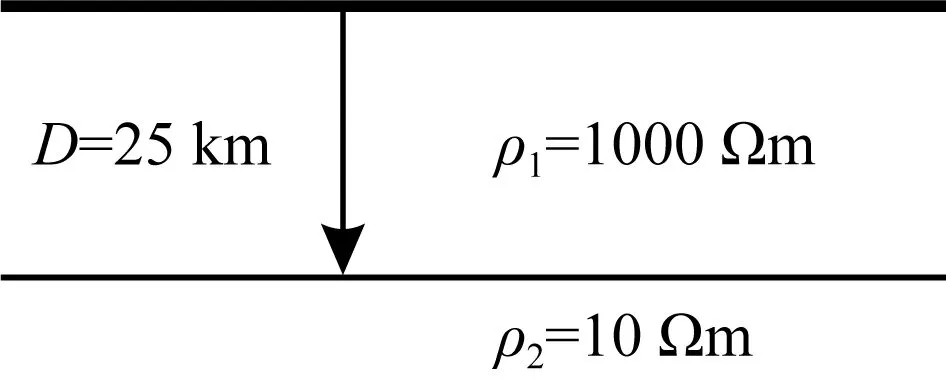
图6 活动区域模型Fig.6 Active region model

场源参数和计算参数与稳定地台区域模型一样，图7为活动区域模型线源正演结果.同样地，活动区域模型两种场源响应在高频段和测点远离源的区域基本一致，在低频段或靠近线源区域差异显著.两种源的相对误差断面图视电阻率的最大相对误差约120%，相位的最大误差44%.以相对误差10%为尺度进行评估，选取与线源水平距离分别为50 km、1000 km、3000 km和5000 km四个不同测点，其视电阻率差异超过10%的周期分别约为3000 s、30000 s、>100000 s、>100000 s，相位差异超过10%的周期分别约为7000 s、35000 s、>100000 s、>100000 s.对比活动区域模型和稳定地台区域模型的最大相对误差值和选取的几个测点位置10%误差频段，明显看到稳定区域模型的场源效应相对活动区域强很多，这表明线源的场源效应会随模型电阻率变大而增强.

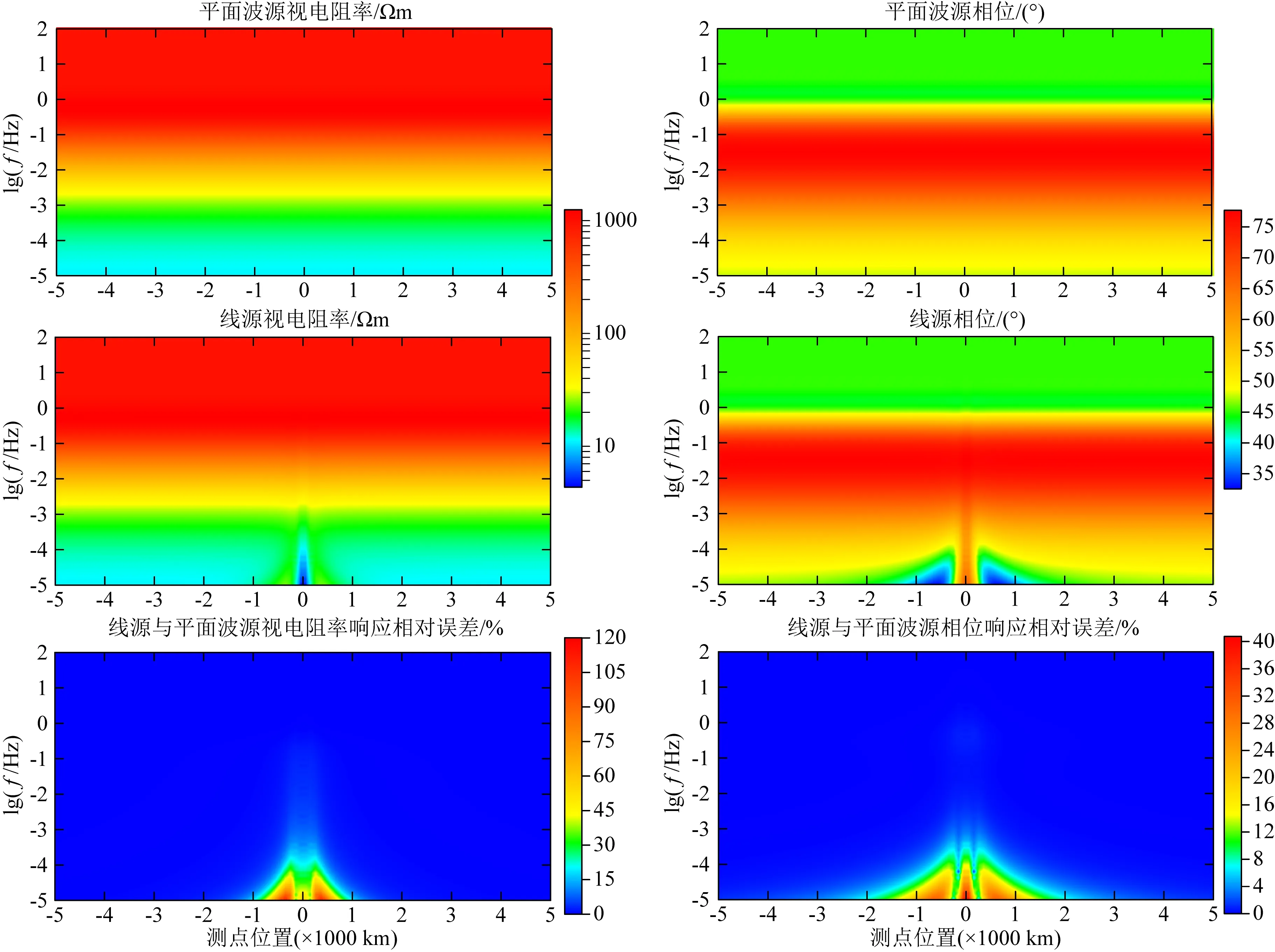
图7 活动区域模型线源与平面波源正演响应及其相对误差Fig.7 Response and relative error between line source and plane wave source in active region model

2 片电流源

极光电集流体系宽度一般为数百至数千公里，用线电流来模拟具有一定的局限性，因此具有一定宽度的片电流源模型更为合理.另外，一些研究者通过极光区的地表磁场观测发现，极光电集流体系横向上存在一定的正太分布(Sobouti，1961)或柯西分布(Park，1973).这里以柯西分布为假设，研究片电流源在地表的电磁响应.

2.1 片电流源一维正演理论

柯西分布是一个数学期望不存在的连续型概率分布，当随机变量满足它的概率密度函数时，服从柯西分布.当峰值位置为0时，柯西分布概率密度函数可表示为

(10)

其中a为峰值一半处的半宽度尺度参数.

根据Boteler等(2000)的推导，具有柯西分布的片电流源在地表不同x位置的电场和磁场分量可表示为关于波数v的正余弦积分：

(12)

(13)

式中的R同样为式(4)表示的关于地下电性结构的地面反射系数.

同样地，采用式(5)—(7)类似的数值滤波计算即可求得式(11)—(13)数值解，并用公式(8)、(9)求得片电流源地表视电阻率和阻抗相位响应.

2.2 片电流源响应分析

将上述片电流电磁响应公式(11)—(13)和线电流源响应公式(1)—(3)对比发现，片电流源与线电流源响应公式的形式相同，只是积分的指数由h变为h+a.这就表明高度为h、半宽度为a的高空片电流源在地表的电磁场响应，与高度为h+a的高空线电流源在地表的电磁场响应相同.

由前面线源不同高度的响应特征分析已经知晓，线源的高度越高场源效应越弱，因此可以知道在同等高度情况下，片源的场源效应要弱于线电流源.由于片源只是增加了一个半宽度a的参数，因此这里只以均匀半空间模型为例，主要分析不同半宽度情况下的片源响应特征，其他模型的片源响应特征可完全参考线源响应.

不同宽度的极光电集流源在地表的电磁响应特征分析具有重要意义.假设片电流源中心处的最大电流100万安培，模型为100 Ωm的均匀半空间，地表测点间距50 km，测点从片源开始至最远距离5000 km处，计算周期T=10000 s时片电流源半宽度分别为100 km、200 km、500 km的地表电磁响应.图8为正演结果，横坐标为测点位置，纵坐标为视电阻率和相位，图中不同颜色的曲线分别代表几种不同半宽度的片电流源响应结果.由于片源可以等效为一定高度的线源，根据计算结果看到，片源与线源响应特征相同，在靠近片源的区域响应值相对于平面波结果发生偏离波动.另外，对于不同半宽度的片源响应则波动幅度不同，片源半宽度越小波动峰值越大，半宽度越大越趋于平面波响应.

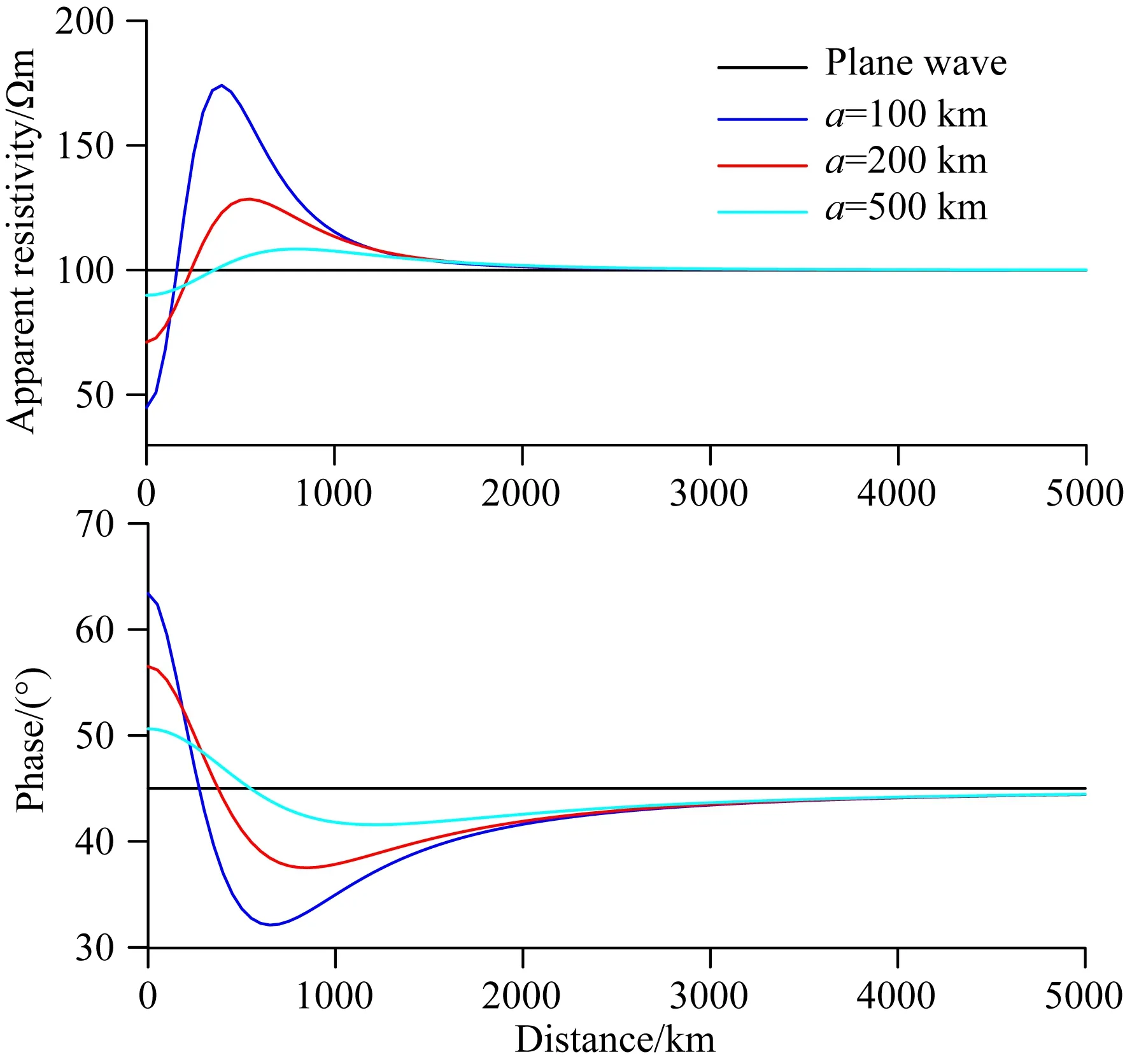
图8 不同半宽度片电流源正演结果Fig.8 Responses of different half widths sheet source

3 波数场源

Price(1962)和Srivastava(1965)研究指出，大地电磁场源特别是在中低纬度地区可能在横向上存在周期性波动，因此引入了场源的影响项ν，即场源横向波动的波数，图9为波数场源和平面波场源的对比示意图.

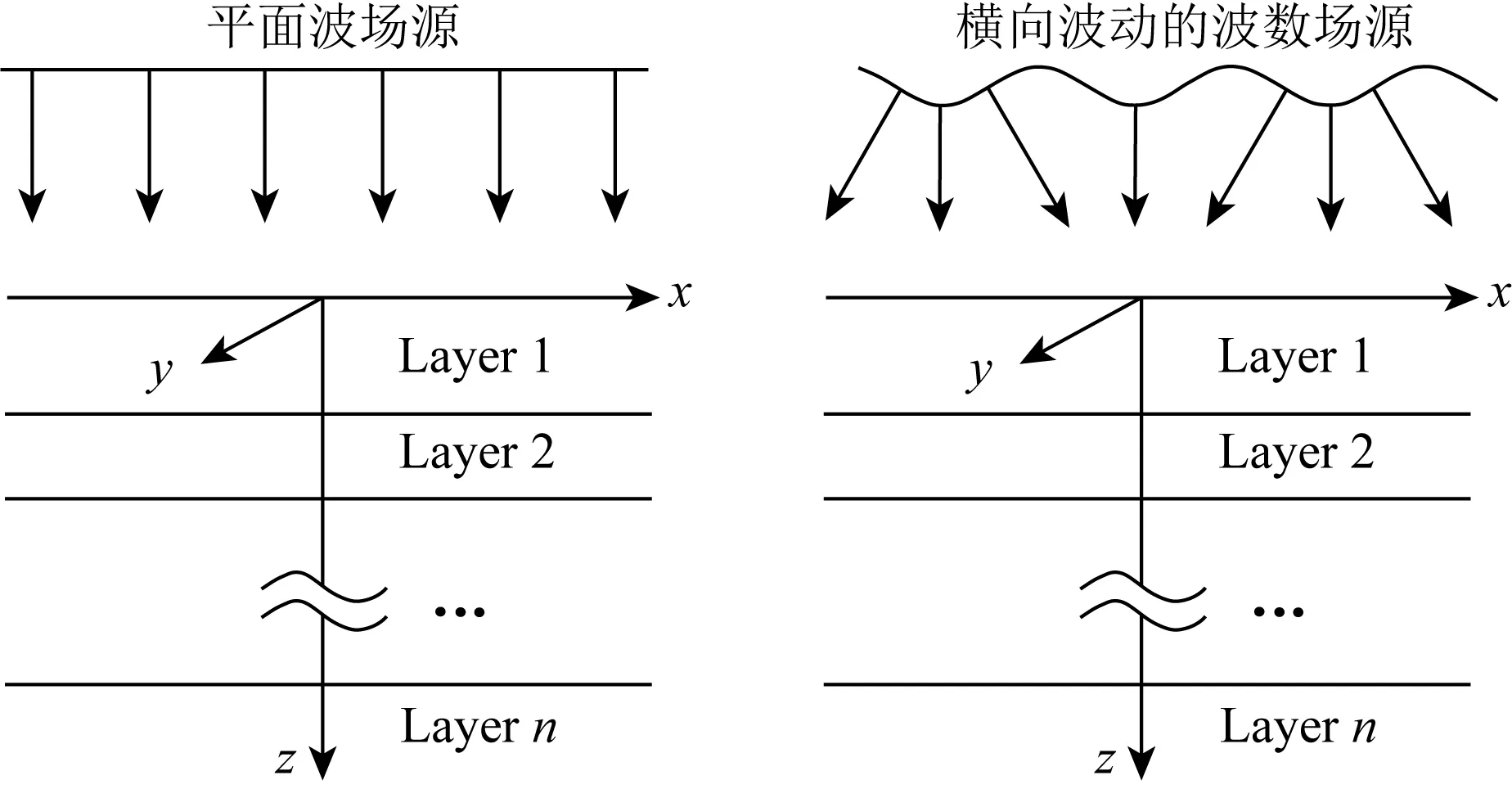
图9 波数场源和平面波源对比示意图Fig.9 Wave number field source and surface source

3.1 波数场电流源一维正演理论

由Maxwell方程组出发，根据Srivastava(1965)的推导，波数场源在大地介质中的阻抗可表示如下形式：

(14)

其中A、B为积分常数，θ2=v2+4πiωσ，v即为场源的横向波数，λ=2π/ν表征场源的横向波长.

可以看到，式(14)的阻抗形式与平面波入射到层状介质的阻抗形式(Cagniard，1953)是一致的，所不同的是用空间波数θ来代替了平面波的波数k.与平面波的推导方式一样，从底层开始通过阻抗递推公式，可得到波数场源在层状介质地表的阻抗公式为

(15)

式中h为模型各层厚度.

3.2 波数场源响应分析

Price(1962)研究波数场源的场源效应时，给出了地球上波数场源横向波数v值范围一般在1.57×10-4～1.57×10-2km-1，对应的横向波长λ值的范围约400～40000 km.因此这里波数场源波长参数分别选择400 km、1200 km、2000 km和无限长，其中无限长等效于平面波.图10和图11分别为100 Ωm及1000 Ωm均匀半空间模型波数源正演响应，横坐标为周期，纵坐标为视电阻率和相位，图中不同颜色的曲线分别代表几种波长的响应结果.

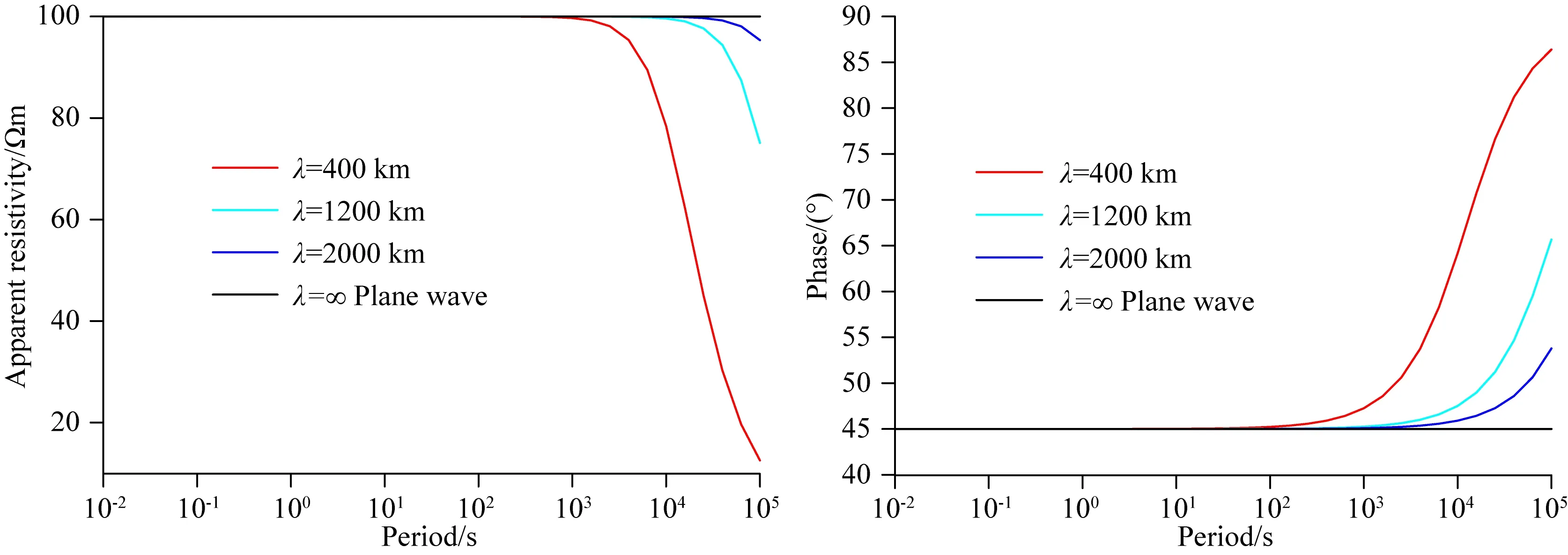
图10 波数场源100 Ωm模型正演响应Fig.10 Responses of wave number field source in 100 Ωm model

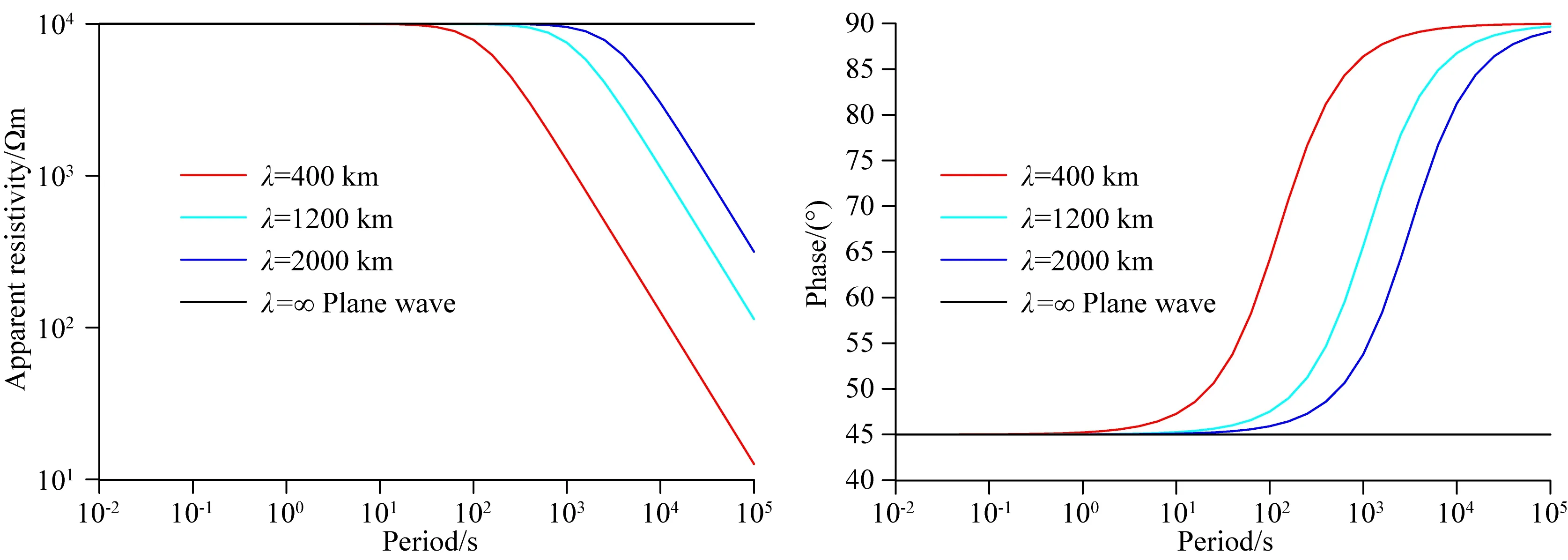
图11 波数场源10000 Ωm模型正演响应Fig.11 Responses of wave number field source in 10000 Ωm model

首先，将任一横向波长正演曲线与平面波响应对比发现，波数场源正演结果在高频段与平面波响应基本重合，随着频率变低，波数场源与平面波场源视电阻率差异和相位差异都逐渐变大，其中视电阻率值逐渐减小，相位值逐渐变大.其次，对比不同波长正演曲线，发现横向波长越短则差异越显著，横向波长越大则越趋于平面波响应.另外，通过对比两种电阻率模型的响应可以看出，1000 Ωm的场源效应程度明显大于100 Ωm模型，以2000 km波长的波数源与平面波视电阻率相位的最大相对误差为例，100 Ωm模型分别为4.66%和19.52%，1000 Ωm模型分别为96.84%、97.99%.分析表明，波数场源的场源效应程度与周期、电阻率和波数大小均正相关.

4 大地电磁场源效应校正方法

通过前述几种典型非平面波场模拟，初步了解了大地电磁场源效应的基本特征，认识到大地电磁的场源效应可能在低频段较为显著.那么在大地电磁特别是低频段的资料处理和反演解释中，就可能有必要开展场源效应校正或考虑场源效应的反演研究.由于目前关于大地电磁的场源效应校正研究较少，本文初步归纳和提出几种校正方法.

4.1 频域截断法

以极光电集流为例，考虑一般情况下最大强度的场源效应，可假设极光电集流为线电流源，高度为90 km，场源平行于纬线位于约66°的极圈边缘.计算位于0°～90°纬度范围内的测点，根据地表距离计算公式，场源与测点距离范围约为0～7338 km.以0°、15°、30°、45°、60°、75°、90°几个不同纬度测点为例，表1是极光电集流场源在各纬度测点场源效应分别为1%和10%的频段值，这里的1%和10%即是指线源与平面波源响应的相对误差.对于不同纬度区域的测点，表1中对应的场源效应影响频段一般为最大情况，小于此频率范围的数据在处理解释中可能就需要考虑场源效应的影响.

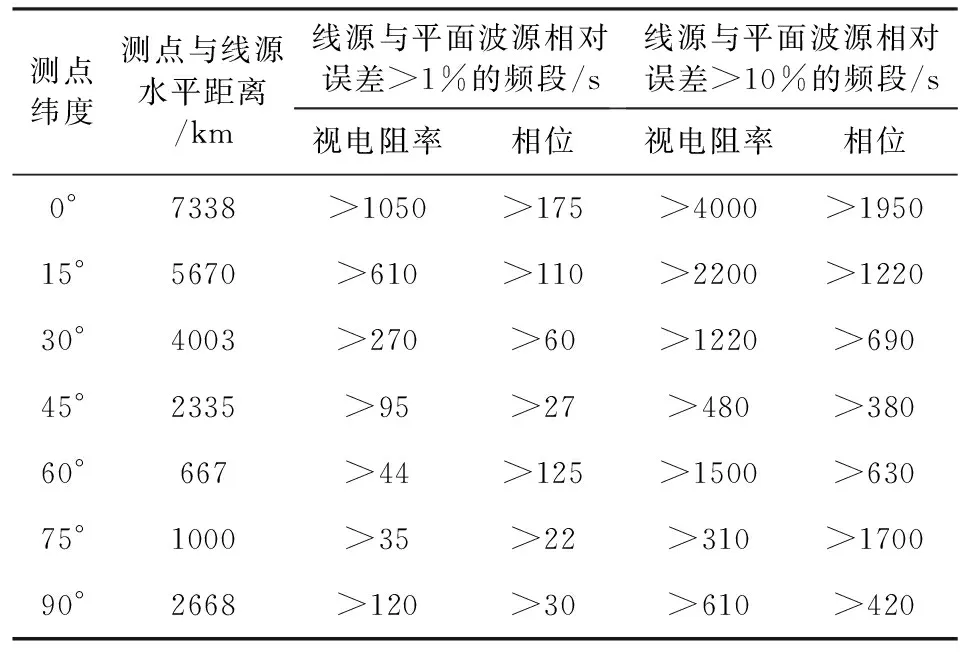
表1 10000 Ωm均匀半空间模型极光电集流场源效应频段Table 1 The source effects spectrum of aurora electric collector field in 10000 Ωm model

4.2 测点平均法

高文(1991)在研究大地电磁场源效应时，指出沿测线方向的平均值可能会更接近均匀场源即平面波场的响应，提出一种“测点平均”校正方法，但并未开展相关模拟.这里以1000 Ωm均匀半空间模型为例，线源高度100 km，周期T=10000 s，分别采用7点算术平均和13点算术平均进行校正，图12为校正前后的视电阻率和相位曲线，校正后的结果场源效应程度有所降低，特别是测点与线电流源一定距离范围内，在远离线源区域校正后的结果场源效应并无明显改善，当用于平均计算的测点数较多时，校正后结果越靠近平面波.

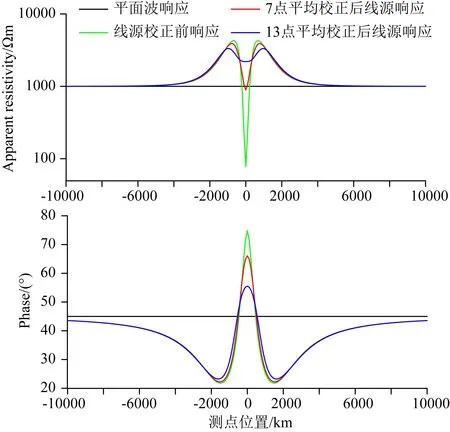
图12 线电流源正演结果测点平均校正前后对比Fig.12 Comparison of average calibration of measuring points before and after in linear current response

4.3 时间域延长法

Lezaeta等(2007)对加拿大北部极圈内1998—2000年长期观测的大地电磁数据做了场源效应分析，首先将观测资料分为每月单独处理，发现各月在周期大于约4000 s后曲线分离，表明不同月份受场源效应影响程度不同.随后再按8个月合并分段处理，发现各段的处理结果基本一致，这表明长期观测对消除或降低场源效应有一定作用.

由于所收集到的大地电磁资料观测时长有限，而地磁台网则具有长期稳定观测的磁场数据，其观测的磁场与大地电磁观测的磁场数据都包含交变场，因而这里以2019年度的北京地磁台站数据为例进行试算.首先将北京地磁台2019年度数据分别按单月进行计算，再分别按1—6月和7—12月半年度进行计算.本文的时频计算采用EMTF处理软件包(Egbert and Booker,1986)，首先计算不同频率段的时间窗大小，对每个时间窗进行时频变换，分别得到各磁场分量的自功率谱和互功率谱，再利用传输函数关系求得倾子幅值TipMag.图13为计算得到的地磁台倾子幅值曲线，黑色曲线为1至12月各单月计算结果，红色和蓝色曲线分别为1—6月和7—12月整体计算结果.通过曲线对比可以看到，不同单月的计算结果在周期几千秒内基本重合，随着频率的变低又逐渐分离，表明低频部分受场源效应影响导致在不同时间段计算结果存在差异.对于按半年度计算的结果，尽管在低频部分仍然存在一定的分离，但两条曲线整体更为接近且靠近各单月计算结果的平均值，表明长期观测能够有效降低场源效应.

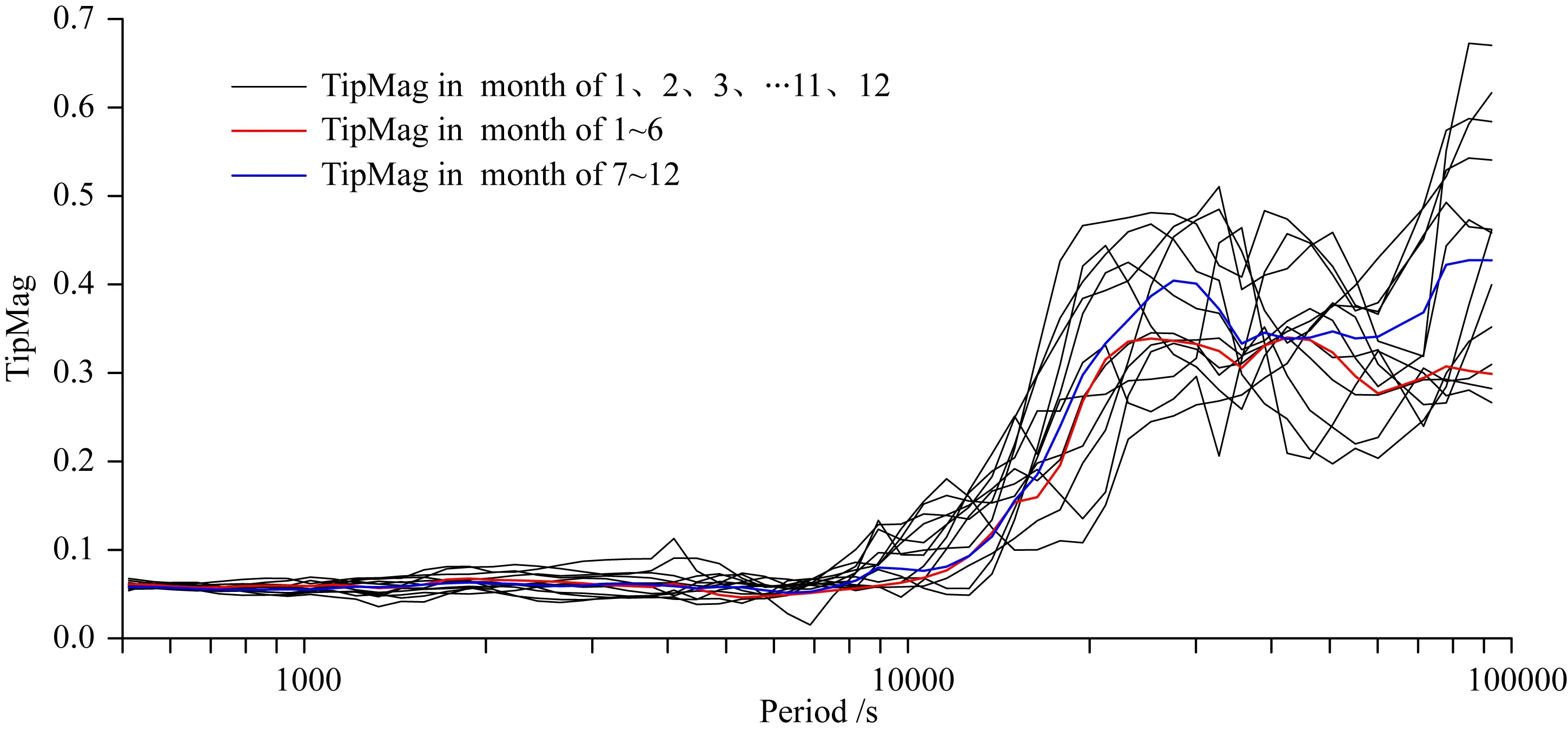
图13 北京地磁台不同观测时长倾子幅值对比Fig.13 TipMag of different observation time at the Beijing Geomagnetic Observatory

4.4 时间域剔除法

Jones和Spratt(2002)通过对1996年8月份在加拿大北部靠近极光区两个星期观测时长的LMT数据进行分析，发现垂直磁场Bz分量对非平面波场的响应较为灵敏，Bz波动幅值相对较强段往往对应场源效应较强时间段.因此，Jones and Spratt指出在对信号进行时频处理前，通过剔除Bz分量波动幅值相对较大时间段的电磁数据可一定程度上降低场源效应影响.由于Jones and Spratt提出的这种时间域剔除校正方法主要是经验和试验所得，并未进行理论模拟说明，这里首先对磁场Bz分量变化情况进行模拟分析.对于层状介质模型，其平面波场的Bz响应值应当为0，而非平面波场的Bz响应可能不为0.这里以线电流源为例，模型选用图4的稳定区域模型，线源电流100万安培，高度100 km，测点位置从与线源水平400～40000 km.从图14的Bz响应断面可以看到，线源Bz响应值的分布特征有两个，一是随频率变低而变大，二是靠近线源则变大，表明Bz分量的强弱对应了受场源效应影响的程度.在实际中，在不同时段、不同区域可能是由多种场源的组合叠加，当其中的非平面波源在测点处产生了响应，则Bz值就可能产生较强的波动变化.

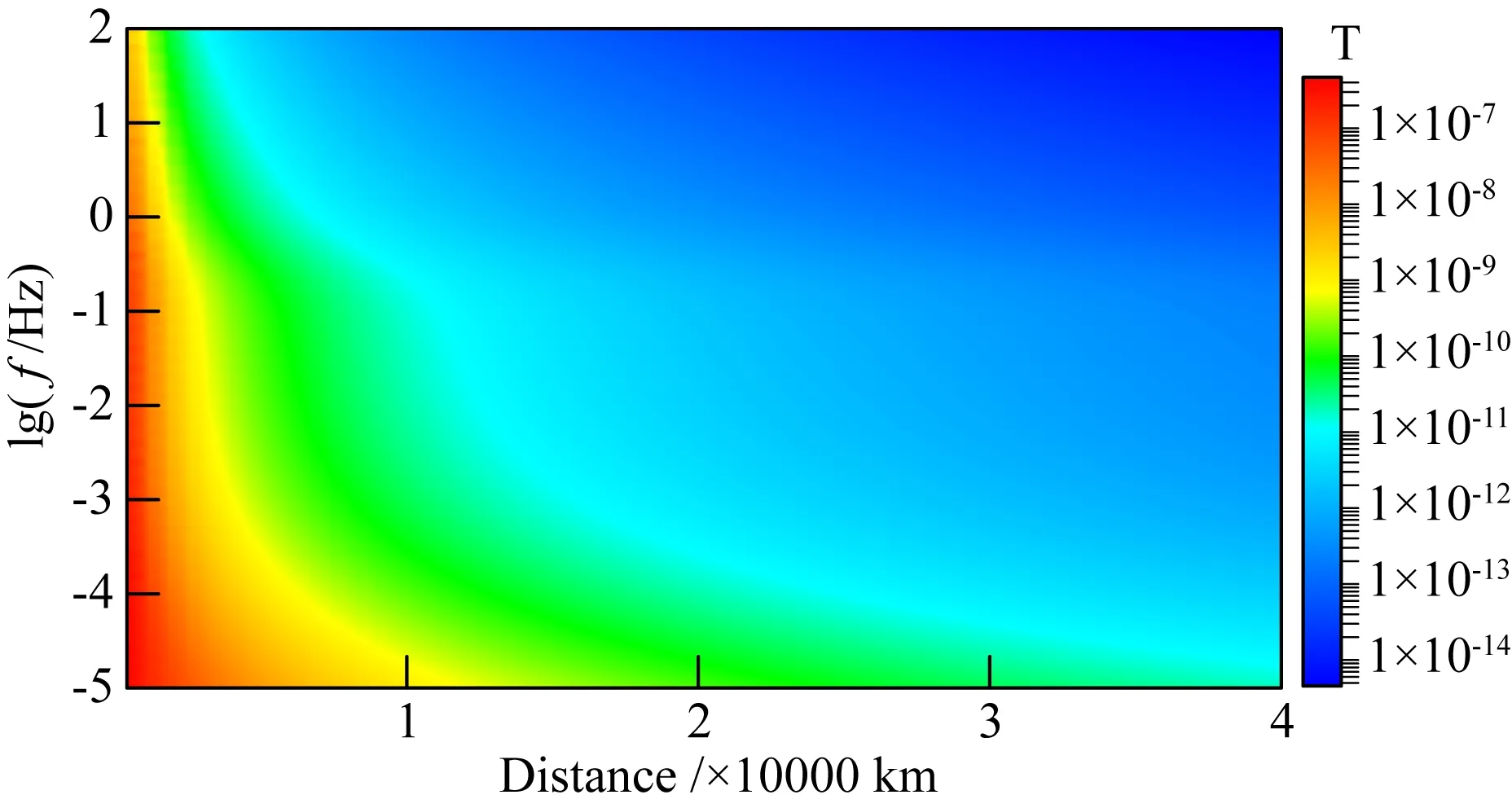
图14 线电流源-稳定区域模型Bz响应断面Fig.14 Bz responses of line current source in stable region model

下面仍以北京地磁台站数据为例进行试算，图15是2019年度北京地磁台的磁场三分量时间序列.为实现时间域剔除校正前后的对比分析，这里以剔除前(图13)计算结果倾子幅值作对比.观察发现图15中Bz较大值主要出现在下半年，因此这里选取7—12月即下半年的数据进行剔除试验，由于Bz波动剔除阈值的设置对计算结果肯定存在一定影响，如何判别场源效应影响所对应的阈值较为复杂，而本文主要目的是试验校正方法的有效性，因此对于具体如何选取阈值这里不做深入研究.参考Jones和Spratt(2002)根据Bz最大波动幅值和分布统计情况设置阈值的方法，以图15中10月份数据为例，将Bz幅值波动超出虚线范围的数据剔除掉.

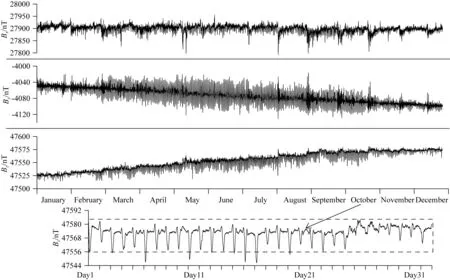
图15 北京地磁台2019年度磁场时间序列Fig.15 The magnetic field time series of Beijing Geomagnetic Platform in 2019

图16为剔除前后的计算结果倾子幅值对比曲线，青色曲线为剔除前10月份单月计算结果，洋红色曲线为剔除后10月份单月计算结果，黑色线为其余月份单月计算结果，红色线和蓝色线分别为上半年以及下半年剔除前结算结果，绿色线为下半年剔除后的结算结果.可以看到，无论是10月单月还是下半年计算结果，剔除Bz波动较大数据后的处理结果更加靠近时间域延长后的曲线，这表明采用时间域剔除方法来降低场源效应影响是有效的.

教学名师通常是学术造诣高、教学水平高、教学质量好且德才兼备的老师才能当选。由教学名师来担当新进教师的岗前培训专家确实可以起到模范带头的作用。自2003年，教育部就开展了第一届高等学校教学名师奖评选，鼓励教授上讲台。此后，地方以及地方高校也纷纷设立不同级别的教学名师奖。教学名师通常长期为本科生授课，积累了丰富的教学经验，可以较好地传授给即将走上讲台的教师把握组织课堂的本领、师生之间沟通的本领、优秀的教学方法和实用的教学手段。教学名师同时也有较高的学术水平，即使面向科研岗位的教师，也能传授前沿的科学知识。

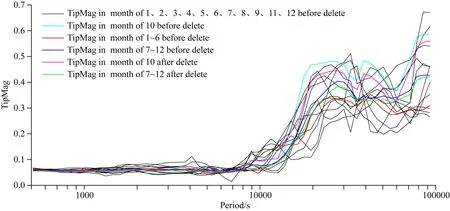
图16 时间域剔除法校正北京地磁台倾子幅值Fig.16 The time domain elimination method corrects the tilting amplitude of the Beijing geomagnetic platform

4.5 考虑场源的大地电磁反演

对于可控源音频大地电磁法，要想利用具有场源效应的资料最直接的办法就是考虑场源的反演.类似的，若在已知场源相关参数的前提下，对天然场大地电磁法也可开展考虑场源的反演.尽管目前对场源形式的识别和相关参数的获取还存在一定困难，但可首先从理论上进行模拟，分析考虑场源效应与否对反演结果的影响特征.根据Tikhonov和Aresenin(1977)的正则化反演理论，反演问题可表述为

ψ(m)=ψd(m)+λψm(m)，

(16)

其中m为模型，ψ(m)为总目标函数，ψd(m)为数据目标函数，ψm(m)为模型约束目标函数，λ为控制模型约束目标函数在总目标函数中的权重正则化因子.基于前述几种非平面波场源的正演理论，本文采用自适应正则化反演策略(陈小斌等，2005)实现了考虑几种不同场源的大地电磁一维反演.

以层状模型为例开展反演计算，模型参考了卫星磁测数据反演的地球平均电阻率模型(Grayver et al., 2017)，一共分为6层，层厚度和电阻率分别为：4 km/100 Ωm、71 km/3000 Ωm、75 km/400 Ωm、50 km/50 Ωm、200 km/10 Ωm、1 Ωm.线电流源相关参数为：高度100 km，测点与源水平距离400 km；片电流源相关参数为：高度100 km，半宽度200 km，测点与源水平距离400 km；波数场源相关参数为：横向波长2000 km.模型采用40层网格，厚度等差递增，反演初始电阻率为100均匀半空间，计算频率范围102～10-5Hz，等对数间隔共36个频点.首先在正演结果中加入3%的随机误差来模拟实测数据，再分别开展几种源的反演，并将几种非平面波源数据采用平面波源进行了反演.图17为反演响应对比和拟合误差收敛曲线，三种场源最终的反演响应曲线与用于合成数据重合度高且拟合误差收敛正常，表明反演算法稳定.图18为地球平均电阻率模型及其反演结果，考虑场源的反演结果曲线与给定的模型曲线拟合度较高，而将具有场源效应的数据进行平面波方式的反演则均产生了一定程度的畸变，畸变程度总体上随深度而变大.表明场源效应对大地电磁深部探测是存在一定影响的，在一定情况下恐难以忽略.

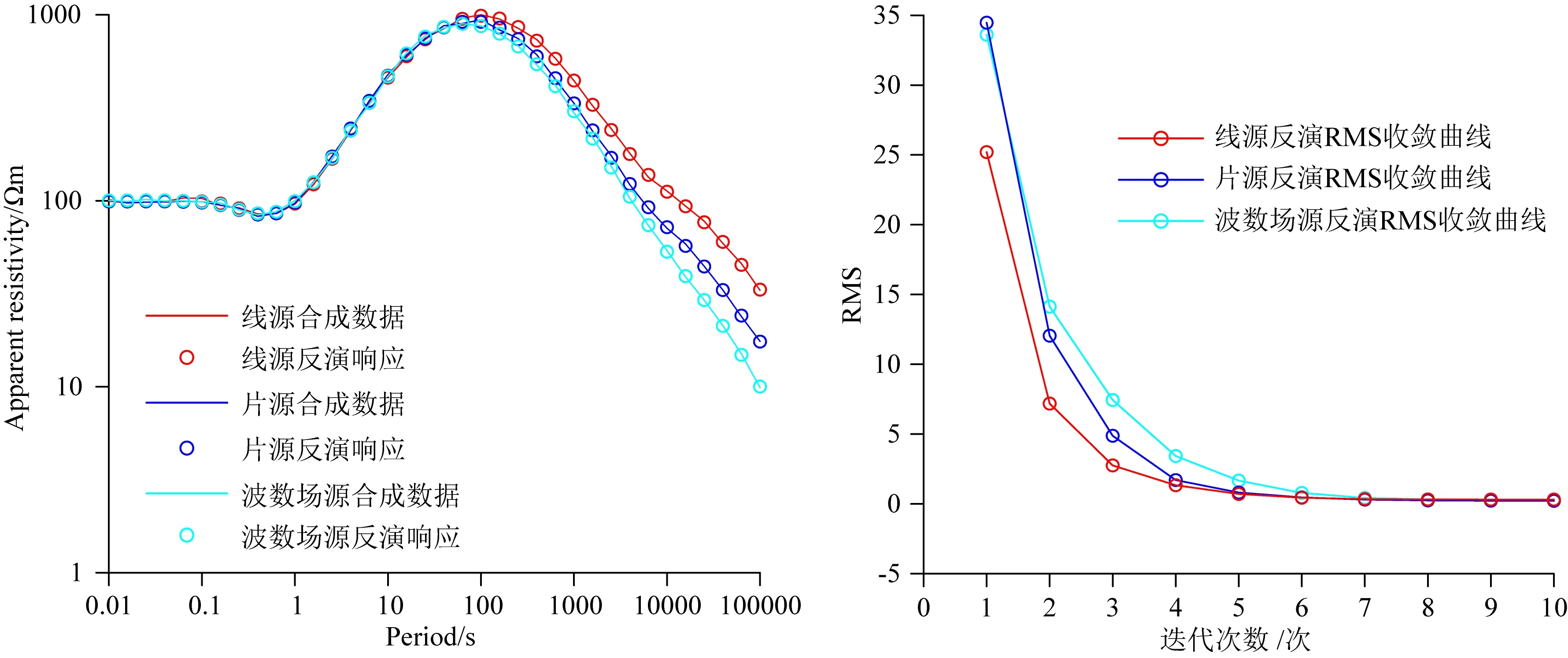
图17 地球平均电阻率模型反演响应和RMS收敛曲线Fig.17 Inversion responses and RMS of earth mean resistivity model

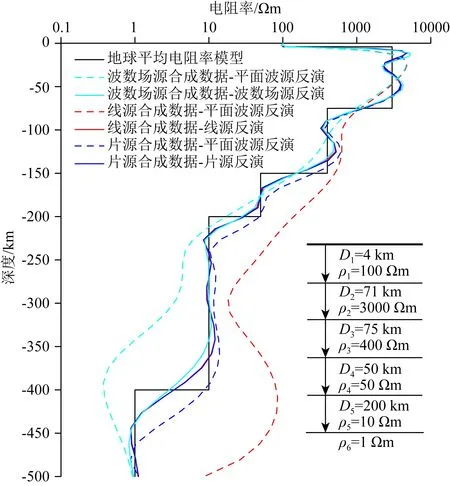
图18 地球平均电阻率模型带源与不带源反演结果Fig.18 Inversion results of earth mean resistivity model with and without source

5 结论

大地电磁场源效应在一些情况下可能无法忽略，本文通过开展线源、片源和波数场源三种典型非平面波场源的一维正演研究，模拟分析了大地电磁场源效应基本特征，并初步归纳和提出了频域截断、测点平均、时间域延长、时间域剔除和考虑场源效应反演几种校正方法，主要取得以下几点认识：

(1)大地电磁场源效应强度与模型平均电阻率正相关，与频率和测点与源水平距离负相关，在诸多情况下已有超过10%的畸变.对于线电流源，场源效应强度与线源高度负相关；对于片电流源，场源效应强度与片源半宽度负相关，其它特征与线源一致；对于波数场源，场源效应强度横向波长负相关.

(2)频域截断法是通过计算极限模型来截断场源效应影响频段，对大地电磁的资料处理解释有一定参考价值.测点平均法通过对多个同步观测的邻近测点进行平均，时间域延长法通过延长测点观测时间，时间域剔除法通过剔除较强垂直磁场分量所对应的场源效应较强段数据，均能一定程度上降低大地电磁场源效应的影响.

(3)对于受场源效应影响的大地电磁数据，直接开展平面波方式的反演则可能在深部产生较大畸变.若在获知场源相关参数的基础上，可开展考虑场源的大地电磁反演来消除场源效应影响.

由于过去关于大地电磁场源问题的研究进展相对缓慢，相关研究成果较少，且场源问题较为复杂，因此本文仅做了一些初步探索研究.大地电磁的天然场源在不同时段、不同位置可能差异显著，在实际应用中，对于场源效应校正研究和考虑场源的正反演研究都应当建立在对场源类型和参数有效识别的基础上，因此开展大地电磁场源效应或场源参数的识别研究具有重要价值.此外，本文仅针对一维模型开展了模拟分析，同时考虑场源问题和地球曲率影响的二、三维研究，也可能是提升大地电磁法勘探效果的重要研究方向.