钻孔体应变对气压和固体潮响应的传递函数——以陕西地区为例

杨小林， 储日升 , 危自根， 盛敏汉， 杨锦玲

1 中国科学院精密测量科学与技术创新研究院， 大地测量与地球动力学国家重点实验室， 武汉 430077 2 中国科学院大学， 北京 100049 3 陕西省地震局， 西安 710068 4 中国地震局地球物理研究所， 北京 100081 5 福建省地震局， 福州 350003

0 引言

精度高(优于10-9)且频带甚宽(零至数百赫兹)的钻孔体应变仪，是一种理想的地球动力学观测仪器．自1968年研制成功以来(Sacks et al．，1971)，便被广泛布设于美国、日本、中国和土耳其等国家．由于该仪器更擅于洞察地壳短期(数秒至数月)的微应变变化(Nikolaidis，2002)，所以成为探赜地震前兆(Stefansson et al．，2011；邱泽华等，2012)、震源物理(Evertson，1975；Furuya and Fukudome，1986；Barbour and Crowell，2017；邱泽华等，2020)、断层滑动(Linde et al．，1996；Takanami et al．，2013)和板块俯冲(Ito et al．，2013；Machida et al．，2018)等动力学过程的“硬核”仪器．

但基于地壳浅表(几十至上千米)的钻孔体应变(以下简称体应变)观测系统是一个复杂系统，它不仅受构造活动的影响，而且还极易被潮汐、气象和水文等诸多非构造因子所驱动．其中，气压和固体潮是两种主要且持续作用于钻孔系统的自然负荷(檜皮久義等，1983；Roeloffs et al．，2004)．不宁唯是，固体地球对气压和固体潮的响应还具有频率依赖性(Agnew，1981；上垣内修，1987；Nakao et al．，1989；Roeloffs et al．，2004；Takemoto et al．，2006；Asai et al．，2009；Canitano et al．，2014；张凌空和牛安福，2019)，而这对不同生命史长构造事件的合理捕捉及动力诊断等尤为不利．因此，在不同频带下如何厘清这两种效应，一直是体应变观测和研究中的一大难点．

然而，其频响特性又蕴含着丰富的钻孔系统和地壳结构等信息．故而在不同频点或频带下，通过拟合理论和实测体应变响应的振幅与相位，便能有效推定区域地壳的弹性结构、孔隙度和渗透性等关键参数(吉川澄夫，1987；Nakao et al．，1989；Kamigaichi，1998；Asai et al．，2009；Roeloffs，2010；Canitano et al．，2014；张凌空和牛安福，2019)．可见，利用气压和固体潮等“噪声”来为钻孔或台基系统等“成像”，也极具应用价值．

一般来讲，体应变系统在数月时段内的稳定性最佳(Nikolaidis，2002)．当不受外界动态应力影响时，该系统可视为一个稳定的线性系统(Bendat and Piersol，2011)．若将气压和固体潮作为激励，体应变作为输出，那么该系统的传递函数不仅能在频域内充分揭示气压和固体潮效应的全貌，而且还携带有钻孔和地壳介质的物性信息．鉴于其独特优势，近年来该方法受到了国外学者的重点关注．例如，Nakao等(1989)采用此方法对日本田沢湖台(Tazawako)的气压响应进行了分析，发现当f<0.24 cpd(cycles per day，简称cpd)时，其传递函数的幅值便会快速增大，相位滞后最高可达～20°；在通过孔弹性模型定量计算后，认为该现象主要是由低频气压引起的地下水流动所致，并据此推定出台基介质的孔隙度和渗透系数．Roeloffs等(2004)和Cherepantsev(2013)则分别对美国PBO项目中的体应变台开展了类似研究，发现当钻孔或台基耦合较差时，气压响应传递函数的幅值便会在f<0.1 cpd时骤降或大幅波动．此外，该方法还被广泛应用于井—含水层和洞体应变系统的研究(Rojstaczer and Agnew，1989；Quilty and Roeloffs，1991；Otsuka，1994；Lai et al．，2013)．目前，我国约有80个体应变台(苏恺之，2003；张凌空等，2012)，虽然针对气压和固体潮效应的研究较多，但仍以最小二乘、回归或小波分析等时域或频域法为主(周龙寿等，2008；张凌空等，2011；张凌空和牛安福，2019)．由于最小二乘和回归分析等时域法没有考虑频响效应(Neumeyer，1995)，所以难以揭示体应变对气压和固体潮响应的频域特征．而从已有的研究结果来看，小波分析的精度与传递函数大致相当(Suto et al.，2006)，但前者可能会受小波基函数的影响(Dierks and Neumeyer，2002；Peng et al．，2009；孙和平等，2018)．相比之下，由钻孔体应变系统自身属性所决定的传递函数(Neumeyer，1995；Bendat and Piersol，2011)，可以更便捷地刻画体应变对气压和固体潮频响的全貌；而且，还能较客观地呈现体应变系统的物性特征(Roeloffs et al.，2004)．所以在频率域，传递函数的适用性更佳．

陕西位于青藏高原、华南和华北块体交汇区，其构造格局复杂且孕震能力较强，历史上曾发生过华县MW8.0强震(图1)．在汶川MW7.9地震前，处于龙门山断裂带NE端的宁陕台，还观测到高频“突跳”的构造应变异常(邱泽华等，2012)．不难看出，该区不同频带体应变信号中可能隐藏着丰富的构造活动信息．而从观测实况来看，区内4个体应变台的气压和固体潮效应却占据主导．

鉴于这种特殊的构造背景和“噪声”特征，无论从地震预测预报的现实需求出发，还是就块体边界带的动力学研究而言，都非常有必要将陕西地区的体应变台作为特例，并应用传递函数来系统诊断其气压和固体潮效应．相关结果，不仅有助于这两种效应的分频改正；而且还能为气压和固体潮响应模型的构建和优化等提供新的视角和实证依据．

1 台站和仪器概况

陕西现有安康、宁陕、西安和乾陵等4个体应变台，主要分布于秦岭造山带中段和华北块体西南缘(图1)，体应变仪均为TJ-2型(苏恺之等，2002)，采样率为1次/min，具体的仪器、台基和地形等信息如表1所示．由于在成孔时，各台钻孔岩芯的物理力学参数并未测定，所以其弹性结构等信息尚属空白．另外，各台雨量计故障多发，因此本文选取了临近气象站的降水数据以作参考．从表1可以看出，仪器探头的安装深度(以下简称孔深)以西安台最浅，乾陵台最深，其余居中．

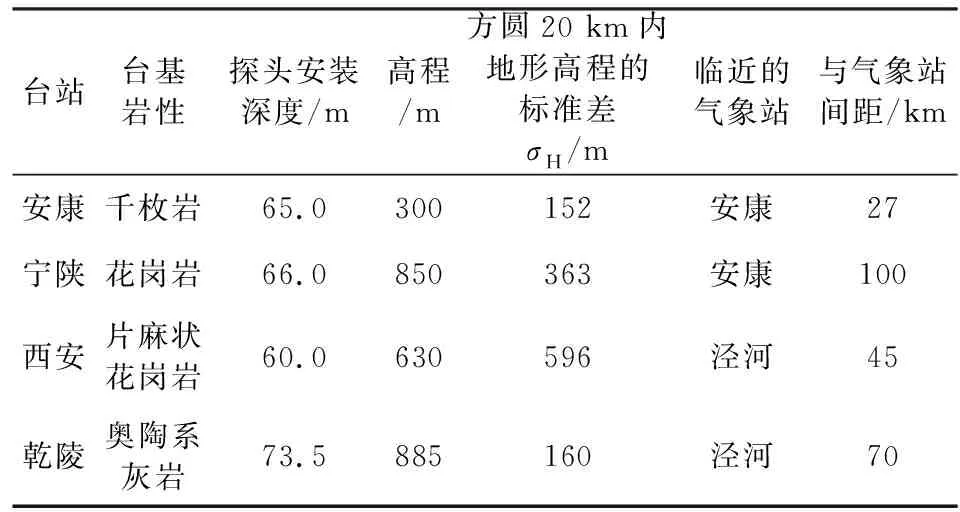
表1 陕西地区4个体应变台站概况Table 1 General information about the 4 borehole dilatometers in Shaanxi Province

此外，为定量描述台域地形的起伏度，本文使用SRTM 90 m分辨率的地形数据(Reuter et al．，2007)，并以台站为圆心提取了方圆20 km范围内所有格点的高程，之后计算其标准差σH．结合表1和图1，可以看出位于盆山耦合带或秦岭山脉的西安和宁陕台，局地地势复杂，相应的标准差也很大，分别为596 m和363 m；而处于盆地内部或边缘的安康和乾陵台，其地势变化就相对平缓，σH也较小．

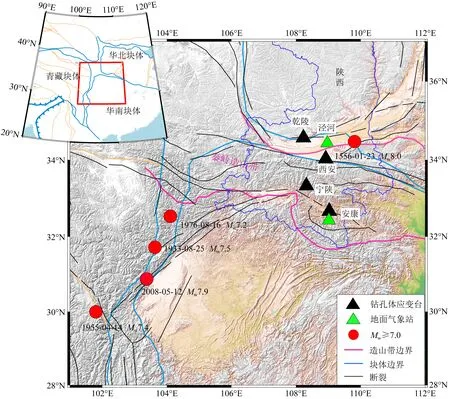
图1 陕西地区构造格局及钻孔体应变台分布图历史强震目录来自董培育等人(2020)的研究，右上角子图中红色矩形框为研究区范围示意图Fig．1 Tectonic setting of Shaanxi Province and the locations of the four borehole dilatometers (black triangles)The green triangles show the two meteorological stations，the red solid circles indicate the epicenters of strong earthquakes with MW≥7.0 (Dong et al．，2020)，the black lines represent the surface fault traces，the pink lines denote the margins of Qinling orogenic belt，the light blue lines denote the tectonic block boundaries for the South and North China blocks， and the Tibetan Plateau，respectively．The red box in the inset map (upper left) indicates the location of the main area of Shaanxi Province and its surrounding regions．

2 数据和预处理

为尽量避免或减少降水和地下水对体应变产生的干扰，本文特意选取了冬季时段共151天的观测记录(2018年10月1日—2019年2月28日)．但在此时段，西安台体应变仪的数采故障频发，因此我们对该台进行了相应调整(2016年10月1日—2017年2月28日)．针对体应变和气压数据中存在的台阶和缺数等问题，本工作采用了人工校正和线性插值等对其进行预处理；同时，也去除了观测数据中的线性趋势．

在降水方面，西安、安康、宁陕和乾陵台的累计降水量，依次约为136 mm、73 mm、73 mm和52 mm．总体来看，各台的降水强度和总量都不大，因此可忽略该因子的影响．而对于地下水而言，鉴于冬季时段的降水补给偏少，地下水位变幅也相对较小，加之各台水位仪运行并不稳定．所以，本文暂不考虑该干扰因子．

从地理位置来看，各台距海岸线均大于1000 km，但海潮负荷的影响可否忽略？为此，本文利用HAMTIDE11A．2011全球海潮模型(Taguchi et al．，2014)，计算了相应时段各台的海潮负荷量，结果显示最大振幅仅为～1.5×10-9，可见该因子的影响量十分微弱．所以，本文仅对理论体应变固体潮(以下简称固体潮)进行了计算．潮汐计算所使用的软件为ETERNA 3.4(Wenzel，1995)，采用的地球模型和潮波表分别为Wahr-Dehant(Dehant，1987)和HW95(Hartmann and Wenzel，1995)．

各台的预处理和固体潮数据，如图2所示．需要说明的是，为呈现气压的绝对变化，本文特意在图2中保留其线性趋势．可以看出，各台的气压和固体潮效应虽不尽一致，但变化形态却都比较清晰，尤其在数日周期，气压和体应变形态的吻合度很高，这说明在时域内潮汐和低频气压起了主导作用．

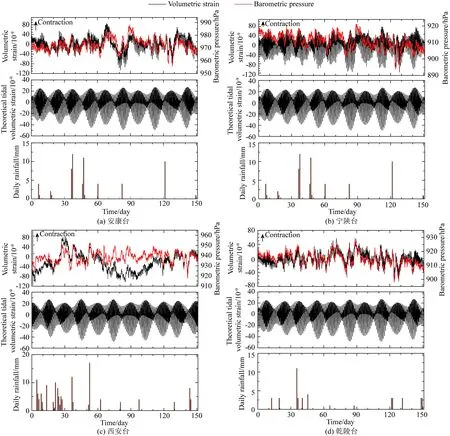
图2 各台体应变、气压、固体潮曲线和日降水量Fig.2 The detrended observed volumetric strains，the observed barometric pressures，the theoretical tidal volumetric strains and the daily rainfalls over 151 days for (a) the Ankang， (b) Ningshan， (c) Xi′an， and (d) Qianling stations， respectively

3 分析方法

3.1 相干函数法

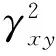
(1)

式中，Gxx(ω)和Gyy(ω)分别为信号x和y的自功率谱，Gxy(ω)为互功率谱．在相干函数分析中，本文以Hamming窗为窗函数，窗长和步长分别取30天和15天．在频率属性的界定上，不同学者的划分依据不尽一致．Roeloffs等(2004)根据体应变仪自身的频响带宽，将频域划分为甚低(f<0.01 cpd)、低(0.01～0.3 cpd)、潮汐(0.3～10 cpd)和高频带(f>10 cpd)；而张凌空和牛安福(2019)则依据体应变对气压响应的理论曲线，来定义高、低频带．由于各台体应变仪和围岩的耦合度不同，加之体应变与井—含水层系统具有一致性(刘序俨等，2017)．因此，本文主要参照Lai等(2013)对高、中、低频带的划分依据，即将体应变受固体潮影响较大的频带定义为中频带(0.5～8 cpd)，f<0.5 cpd为低频带，f>8 cpd则为高频带．

3.2 传递函数法

体应变对不同周期气压和固体潮激励响应的传递函数，可通过求解以下矩阵获得(Rojstaczer，1988a，b；Bendat and Piersol，2011；)：

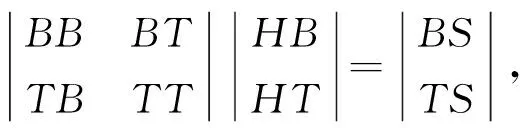
(2)

式中，BB和TT分别表示气压和固体潮的自功率谱，BT为气压和固体潮间的互功率谱，TB是BT的复数共轭，BS和TS分别为气压和体应变、固体潮和体应变之间的互功率谱，HB和HT依次为体应变对不同周期气压和固体潮响应的传递函数．

由方程(2)可进一步推导出HB和HT的表达式：

(3)

(4)

由于在高、低频带，固体潮的影响较弱，故而体应变对气压响应的传递函数可简化为BS(ω)/BB(ω)；在中频带，则分别要对气压和固体潮响应的传递函数展开计算(式(3)，(4))．其中，传递函数的模和幅角依次对应于幅频响应(气压系数或潮汐因子)和相频响应(相位移动)．

若要提取更高质量的传递函数，就需将预处理数据截成多个信号长度为2N的子记录，并在相同频点处计算各子记录传递函数的均值，其目的主要是为了提高信噪比(Lyons，2004；Doan et al．，2006)．详细的参数和计算流程，主要参照了Lai等(2013)所采用的信号处理方法．在低频带，首先对体应变和气压进行2阶Butterworth带通滤波，以滤取1 h～12 d周期的信号，然后每216min(～45.5 d)作为一个记录，计算其功率谱和互功率谱，Hamming窗的窗长和步长分别取～11.4 d和～5.7 d；在中频带，滤波范围为3 min～3 d，将每215min(～22.8 d)作为一个记录，Hamming窗的窗长和步长分别取～2.8 d和～1.4 d；由于高频带体应变和气压数据的信噪比较低，需要对传递函数进行叠加处理以抑制噪声；因此，在高频带，我们将214min(～11.4 d)作为一个记录，滤波范围则与中频带一致，Hamming窗的窗长和步长分别取～8.5 h和～4.3 h．

另外，为客观评价各台气压系数的稳定性，本文也计算了每个频点的变异系数CV(Beyer，1987)：

(5)

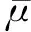
4 结果和分析

4.1 相干函数诊断

图3为各台体应变、气压和固体潮信号在不同频带的相干函数变化，对比之后可以看出以下特征：

(1)体应变和气压：在低频部分(0.1～0.5 cpd)，各台相干函数值普遍高于0.8，其中，安康和乾陵台略有波动，非线性变化明显，其他台则较为恒定基本接近于1，说明体应变和气压在该频段的相关性非常好．而当f<0.1 cpd时，相干函数值就骤减至中等或弱相关，表明在更低频段，气压对体应变影响的程度会迅速降低．在中频带，由于气压在O1和M2频点的能量很小，所以二者的相关系数明显下降．但在其他大部分频点(除乾陵台外)，都呈现强相关．可见，在中频带，乾陵台的相关性最弱且变化极为复杂；究其原因，可能与台基周边黄土沉积层的覆盖范围和厚度等相关．在高频带，乾陵台呈现出单峰变化，并在～20 cpd处达到峰值(>0.9)，表明该卓越周期(～70 min)的高频气压波对体应变的影响最强．需要指出的是，该周期所对应的气压波长为～50 km(Green，1999)．引起该现象的原因，可能与场地效应和大气系统等有关．其他台在高频带的相干性大致随频率增大而呈指数减小，这主要是由于频率越高，气压波的能量就越弱，体应变的信噪比也相应减小．

(2)体应变和固体潮：在日波和半日波频段的相干函数值几乎为1，其中NO1和L2波因振幅较小，所以其相干性略降，其他频率则基本低于0.5．这些特征表明，在～1 cpd/～2 cpd频段，各台体应变和固体潮的相关性都很高．

(3)气压和固体潮：S1和S2波处的相干性较高，但相比而言，S2大气潮的能量更大，其相干性就更好．对于不含噪声的固体潮，其能量主要集中在日波/半日波频段，所以非潮汐频段的相干函数值基本小于0.5．但在高频带的更高频段，部分值明显大于0.5，这可能是由于气压随机扰动或背景噪声所致．

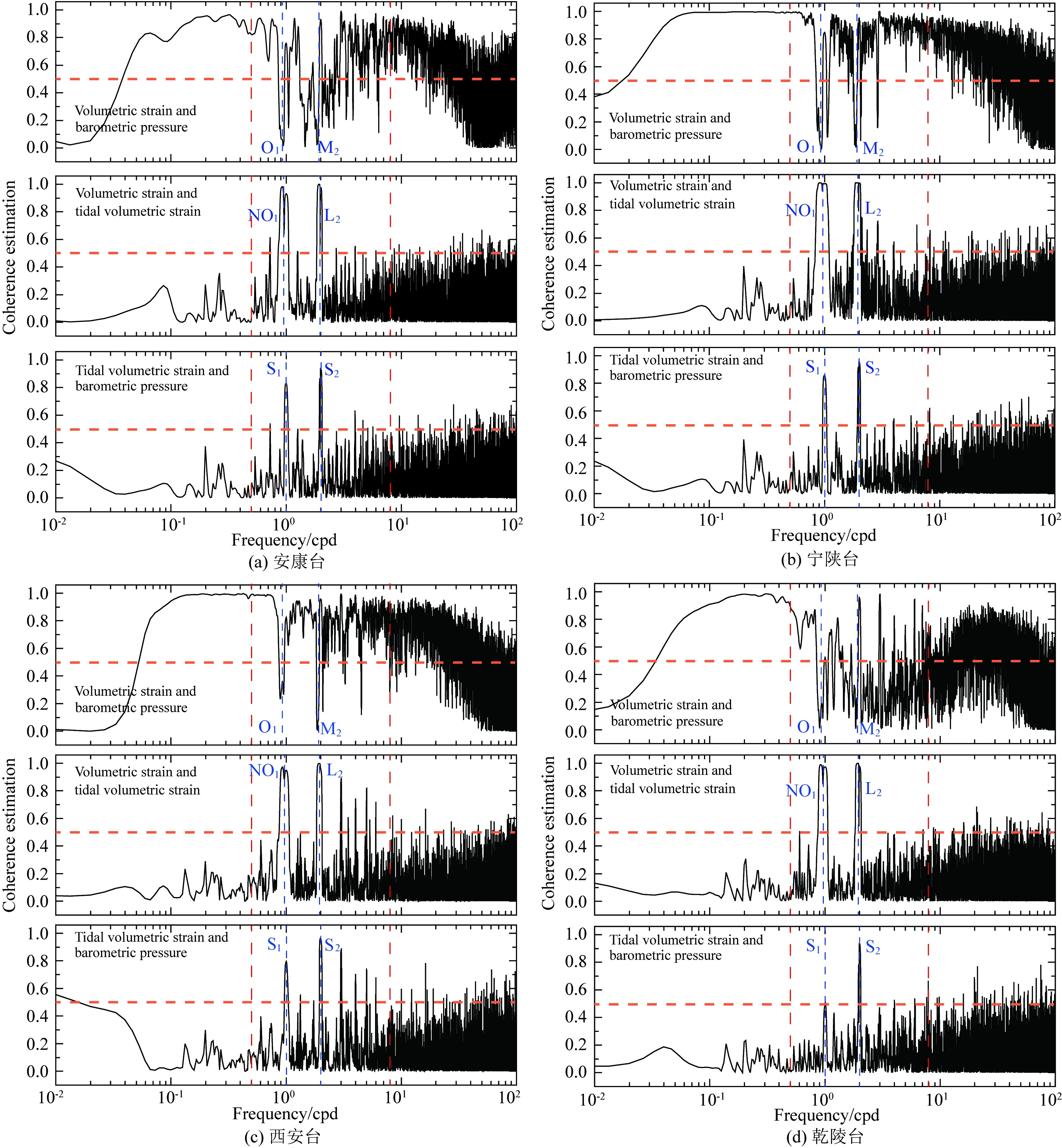
图3 体应变、气压和固体潮三者两两之间的相干函数(a) 安康台; (b) 宁陕台; (c) 西安台; (d) 乾陵台. O1、M2、NO1、L2、S1和S2等潮波频点由竖向蓝色虚线所示.Fig.3 The coherence functions among volumetric strain， barometric pressure， theoretical tidal volumetric strain for the (a) Ankang， (b) Ningshan， (c) Xi′an， and (d) Qianling stations，respectivelyThe red dashed vertical lines mark the frequencies of 0.5 cpd (left) and 8 cpd (right)， respectively．The orange dashed horizontal lines indicate that the coherence functions equal to 0.5．The blue dashed vertical lines indicate the exact frequencies of the main tidal constituents．

总体来看，各台相干函数的局域特征有所不同，但共性特征却十分鲜明：低频部分，气压为主导因子；在中频带，由于气压和固体潮综合作用，所以相干函数在日波和半日波等潮汐频段波动较大；而在高频部分，气压和体应变的相关性随频率增加而呈指数衰减的趋势．

4.2 气压响应的传递函数诊断

从以上分析可以看出，在0.1～30 cpd频带，各台气压和体应变整体上强相关．因此，本文重点对该频带的传递函数进行了分析和探讨．特别要注明的是，该频带所对应的气压波长范围约为10000～30 km(Green，1999)．在高、中、低频带，我们分别提取到13个、7个和3个传递函数；之后，又计算了同一频点处所有传递函数的均值，置信区间取95%．另外，也分别对不同频带气压系数的平均变异系数进行了解算．具体结果，如图4和表2所示．可以看出，各台传递函数整体的连续性都较高，个性和共性特征也十分明显．以下先对每个台的气压响应特征和物理机制等进行探讨：

(1)安康台：在日波频段，气压系数显著波动，相位略有超前，其潜在的诱因可能是S1波的热弹性效应(Lu and Wen，2017)．其他频率的气压系数变化则相对稳定，其中，高、低频带的变异系数相对较小，均在7%左右；但在高频带，相位滞后明显偏大，平均为6.63°，这可能与近地表风化层或裂隙等非弹性介质的滞后效应有关．总体来看，该台气压系数的变幅很小(0.45×10-9/hPa)，相移基本在0°上下，二者的频响效应不明显，均呈现出平稳的线性变化．这一方面说明体应变仪与钻孔围岩的耦合度较高，另外，也表明区域地壳介质的各向异性小、弹性性能好，能以线弹性变形的方式即时响应不同周期的气压负荷．

(2)宁陕台：气压系数在日波频段的波动幅度有所加剧，相位变化离散且大幅超前，最高达～12°(f=1.05 cpd)，即体应变超前响应气压～48 min，这说明S1波对该台的影响可能更甚．其他频率则相对稳定，但气压系数却随频率减小而线性增加．可见，随着气压波长的递增，地下介质的等效弹性强度在逐渐弱化，这可能是受造山带内较大的断裂系统和复杂的地质结构等因素影响．结合表2，可以发现各频带相位滞后的平均值都偏大，其中，高频带竟达8.81°．另一个值得注意的现象是，高频带的相位滞后随频率的增加而波动上升，并于29.8 cpd频点处达到峰值16.31°(滞后～2 min)．而就线弹性介质对气压的理论响应而言，高频带的相位滞后应为0°．产生该显著差异的原因，可能是山区复杂多变的地形地质结构，增加了高频气压场及其能量传递的复杂度(Roeloffs et al．，2004)．

(3)西安台：该台低频带的气压系数基本为常数，约为5.25×10-9/hPa；中、高频带气压系数的变异性略有增加；其中，高频带气压系数的减小速率明显加剧，说明区域浅表介质的阻尼效应较强．由低频到高频带，气压系数相应从5.68×10-9/hPa快速减小至2.89×10-9/hPa，非线性频响的特征极为明显．而相移在中、低频带皆小幅滞后，并于11.4 cpd频点处达到峰值～14°(滞后～5 min)，之后便呈指数下降．导致该现象的主因，可能是周期越小的气压波，其压力在地层中的传播速度会更快．但当f>25 cpd后，相移却出现了小幅的超前变化，这一异常响应可能与浅表的塑性变形或大气压力扩散等有关(Rojstaczer，1988b；肖建清等，2010)．

(4)乾陵台：在低频带，气压系数的稳定性较高，其平均值和变异系数都很小，分别为2.89×10-9/hPa、4.9%；但相移却随频率的降低而线性增大，即从-1.77°滞后至9.23°，这可能是由于该台周边黄土覆盖层的范围广，厚度深，土体的非弹性滞后效应会随区域的扩大而增强(王志杰等，2010；王海云，2011；李智超等，2015)．而中、高频带的气压系数和相移都极为离散，变异系数也很大．究其原因，可能是受弹塑性岩土介质复杂的力学及变形特性影响．

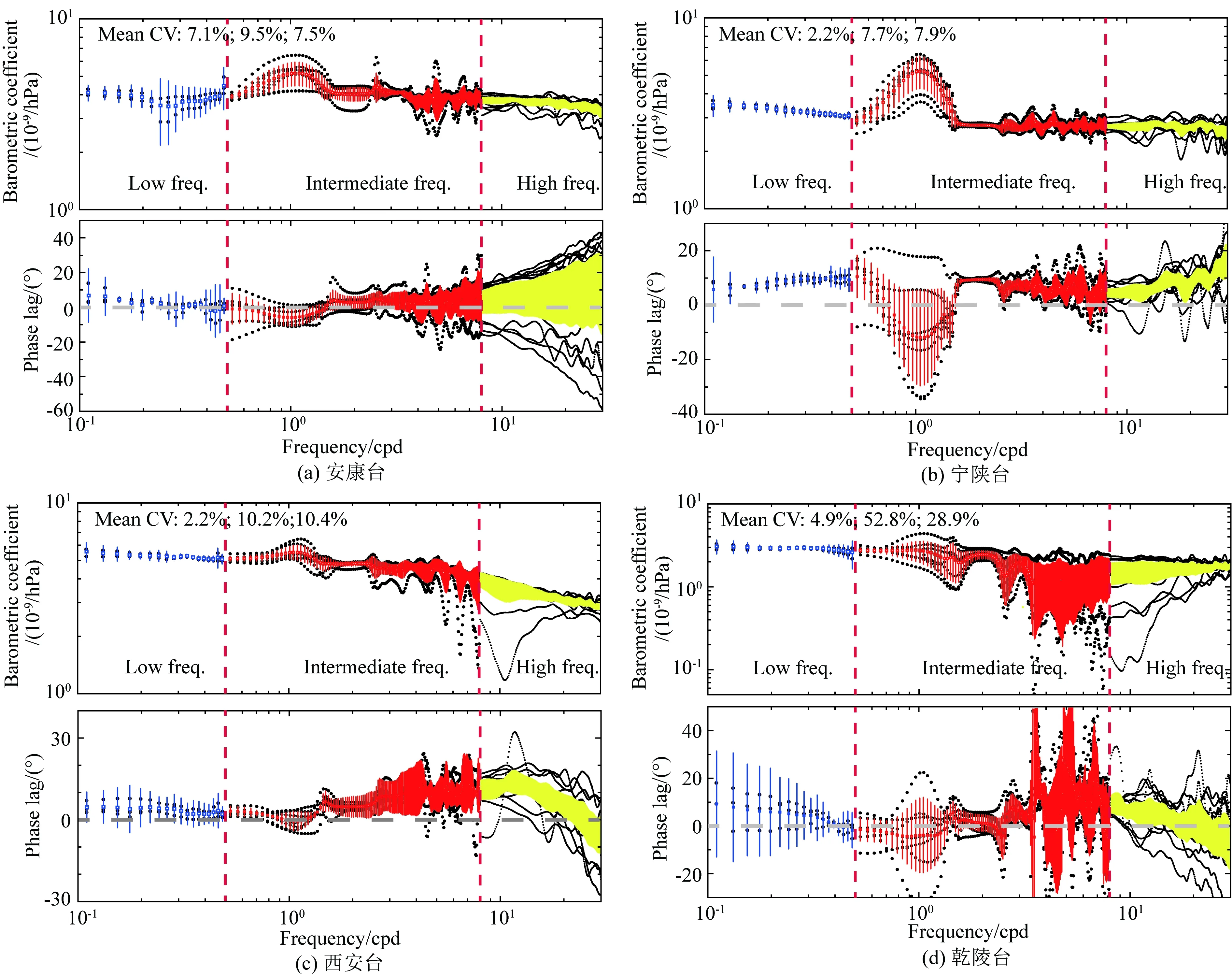
图4 各台不同频带体应变对气压响应的传递函数(气压系数和相移，黑色圆点)(a) 安康台; (b) 宁陕台; (c) 西安台; (d) 乾陵台. 蓝色、红色和黄色空心方格分别为低、中和高频带同一频点的均值，与之对应的竖线表示95%的置信区间，相位滞后值为负表示体应变超前响应气压．不同频带气压系数的变异系数均值由mean CV依次给出．Fig.4 The barometric coefficients，phase lags (black dots)and the corresponding mean coefficients of variation in the low-，intermediate-，and high frequency band by cross-spectra estimation for the Ankang (a)， Ningshan (b)， Xi′an (c)， and Qianling (d) stations， respectivelyThe blue， red， and yellow open squares with vertical lines indicate the average values with the 95% confidence interval in the three frequency band，respectively． Negative phase lags mean phase advance． The mean variation coefficients of barometric coefficients in three frequency bands are given by mean CV． The red dashed vertical lines mark the 0.5 cpd and 8 cpd， respectively． The gray dashed horizontal lines mark the zero-phase lags．

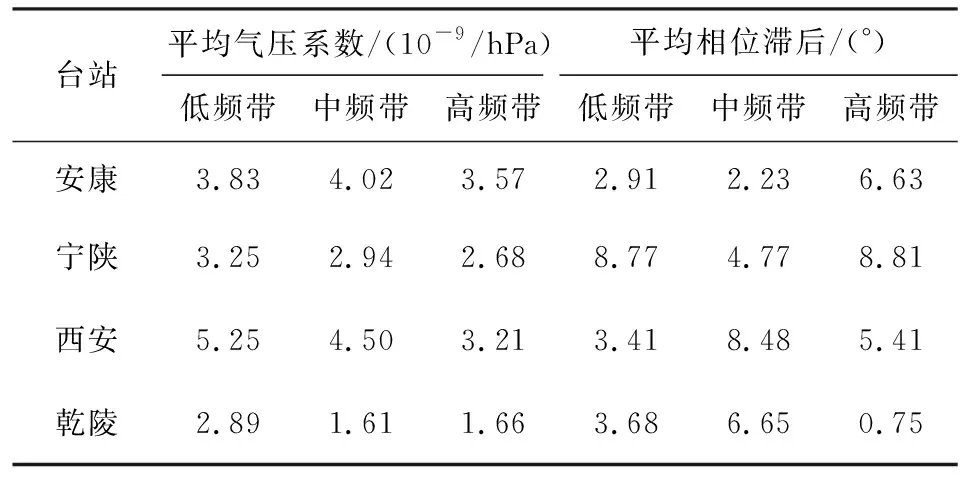
表2 各台不同频带气压系数和相位滞后的平均值Table 2 The average barometric coefficients and average phase lags in low-，intermediate-，and high frequency band for the four stations，respectively

综上分析，各台气压响应的共性特征可归纳为：低频带传递函数的稳定性和可靠性都很高，高频带次之，中频带则最差．不难理解，在低频带，能量强且波长大的长周期气压波，不易受中小尺度各向异性介质的影响；加之，固体潮和低频体应变的物理关联较小．因此，该频带体应变信号中的气压成分就占了主导．相比之下，高频气压的能量微弱；加之地形、局部或区域地壳介质各向异性等因素，使得其激励方式更为杂度．因此，高频体应变和气压的信噪比都急剧下降．但通过叠加传递函数，我们仍可获取相对稳定可靠的高频气压响应．而在中频带，由于受到S1等潮波的影响，气压响应的稳定性就有所劣化．

但就全频带响应而言，当忽略日波频段的影响，安康台的气压响应近线性平稳，宁陕和西安台的气压系数均随频率增大而呈非线性衰减的趋势，乾陵台的非平稳非线性特征最为突出．以上趋势特征的多样化，也表征出不同频带气压响应的高度复杂性和丰富的动力学机制．再进一步对比各台低频带气压系数的平均值(表2)，可以发现西安台最大，乾陵台最小，二者相差近两倍．差异为何如此之大？可能是由于前者钻孔围岩的弹性模量或泊松比较小(张凌空等，2011)，而后者反之；当然，也或许是受黄土介质非弹性衰减作用的(叠加)影响．

需要指出的是，由于钻孔岩芯的力学参数尚未实测，所以难以求出各井孔真实的耦合系数．本文给出的仅为“视”气压系数，因此各台之间不具绝对的可比性．

4.3 固体潮响应的传递函数诊断

鉴于固体潮能量主要集中在日波和半日波频段，因此我们仅计算了0.5～2.5 cpd频带的固体潮响应传递函数．从图5可以看出，各台在半日波频段都较为稳定收敛，而日波频段则相对离散，导致该现象的物理原因可能如下：(1)S1地表温度潮汐的热弹效应(Lu and Wen，2017)；(2)K1波受地球液核章动干扰(Doan et al．，2006)；(3)周日气压波影响(张凌空等，2008)．

为进一步验证固体潮响应传递函数的可靠性，我们采用ETERNA 3.4标准调和分析软件(Wenzel，1995)，在时域内计算了气压影响下的O1、S1K1、M2、S2等4个主要的潮波参数，具体结果如图5所示．对比传递函数的振幅谱，可以看出O1波的潮汐因子偏离最为明显，其中，宁陕台相差高达～0.6．这可能是最小二乘法使用了全频带的平均气压导纳值，故而不足以准确校正O1波中的气压成分；此外，热弹效应也会影响O1波的振幅，因此该潮波参数的可信度和稳定性不高(Bower，1983；Doan et al．，2006)．其他3个潮波则基本吻合，仅以潮汐分析中最常用的M2波为例，可以看出这两种方法所给出的结果非常一致(表3)．综上可见，传递函数给出中频带的连续固体潮响应是合理可靠的．

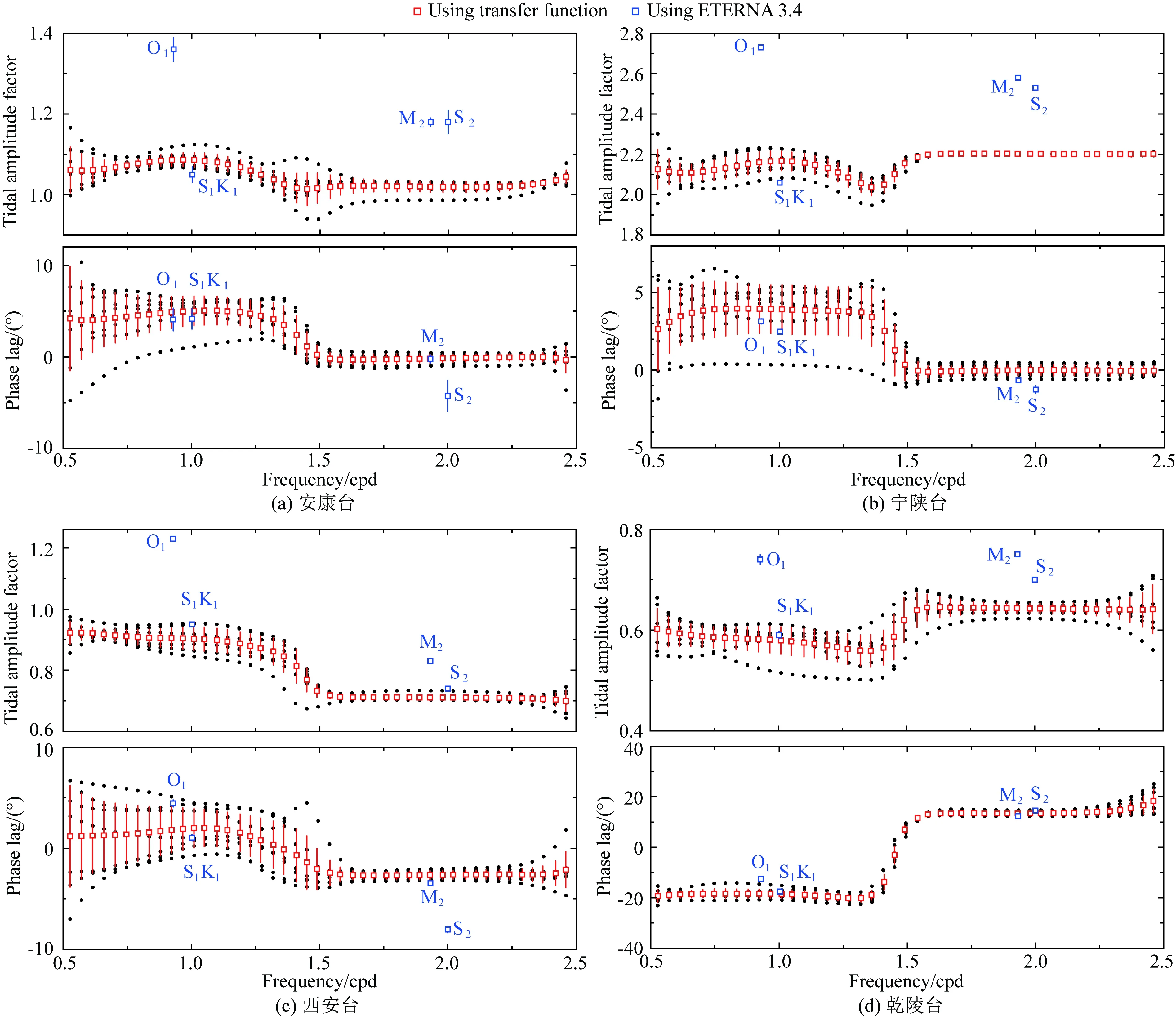
图5 各台体应变对固体潮响应的传递函数(潮汐因子和相移，黑色圆点)(a) 安康台; (b) 宁陕台; (c) 西安台; (d) 乾陵台. 红色空心方格为同一频点的均值，蓝色空心方格为ETERNA 3.4计算的潮波参数． 红色和蓝色竖线分别表示95%的置信区间、标准偏差，相位滞后为负值表示体应变超前响应固体潮．Fig.5 The tidal volumetric amplitude factors and the corresponding phase lags from the diurnal to semidiurnal frequency band (black dots) for the Ankang (a)， Ningshan (b)， Xi′an (c)， and Qianling (d) stations， respectivelyThe red open squares indicate the average tidal volumetric amplitude factors and phase delays at the same frequency points，the blue open squares indicate tidal volumetric amplitude factors and phase delays from ETERNA 3.4 analysis．The red and blue vertical lines mark the 95% confidence interval， and standard deviation， respectively． Main tidal waves are identified with their name． Negative phase lags mean phase advance．

表3 传递函数和ETERNA 3.4提取的M2波参数对比Table 3 Comparison of the M2 tidal responses from the transfer functions and the ETERNA 3.4 for the four stations， respectively

此外，再对比各台M2波的潮汐因子，可以发现宁陕台的固体潮响应最好，安康台次之，西安和乾陵台则稍差．一般来讲，M2波的潮汐因子与钻孔围岩的弹性模量呈负相关(Asai et al．，2009；李进武和邱泽华，2014)．但受到钻孔局部效应、区域地形地质结构、体应变标定和地潮模型等因素影响，该潮波参数的误差可能较大(Beaumont and Berger，1975；Berger and Beaumont，1976；Takemoto et al．，2006；Langbein，2010)．所以，在没有确凿的钻孔围岩力学参数的情况下，深入讨论各台潮汐响应差异的物理机制就显得非常困难．

5 钻孔围岩力学参数的估算

依据体应变观测的双衬套力学模型，当气压波作用于各向同性的线弹性介质时，体应变会即时响应(即相移为0°)，理论气压系数相应为(张凌空和牛安福，2019)

(6)

(7)

(8)

(9)

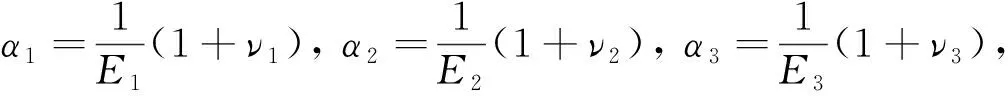
(10)

(11)

式(6)，(7)分别为气压波周期在12 h以内和之外的气压系数解析解，k为体应变仪钢筒内壁面应变与空孔岩石面应变之比，x4是与体应变观测系统各参数相关的一个常数．其中，z为气压的波及深度，l是气压波长，E1、v1、E2、v2、E3、v3分别为钢筒、膨胀水泥、钻孔围岩的弹性模量和泊松比，r1、r2、r3各为钢筒内半径、外半径和钻孔半径．我国TJ-2型体应变钻孔和仪器的相关参数如下：E1=21×1010Pa，v1=0.3，E2=3×1010Pa，v2=0.25，r1=42 mm，r2=44.5 mm，r3=65 mm(张凌空和牛安福，2019)．

从式(6)的定量表达形式可以看出，气压系数敏感依赖于孔深、钻孔围岩力学参数和气压波周期等多个变量．因此当气压周期<12 h，气压响应就变得非常复杂．反之，则主要取决于E3和v3，气压系数也演变为常数．不难看出，利用低频带的气压系数来估算钻孔围岩的弹性强度相对更可行．但在解唯一的情况下，仅通过式(7)来求解两个变量就变得相当艰巨．所以，本文采取折中(trade-off)的思路来处理该问题．

若不考虑潮汐频点的波动，安康台的气压系数在整个频带内变幅最小(1×10-9/hPa)，相位谱接近于0°，说明该台体应变仪与钻孔围岩耦合程度高、区域介质的各向异性小，阻尼力弱．而这些特征与上述模型所假设的介质条件十分契合，因此，本文重点对安康台的钻孔围岩力学参数进行解算．另外，考虑到低频带气压的能量较大，气压系数也更加稳定可靠．所以为了获取更准确客观的力学参数，我们以低频带的平均气压系数3.834587×10-9/hPa为约束，并利用式(7)进行匹配计算．由于安康台的台基岩性为千枚岩，同时，借鉴相关岩石力学试验的结果(Abdaqadir and Alshkane，2018；吴永胜等，2018)，本文对该台钻孔围岩的弹性模量和泊松比进行了推定，最佳值分别为79.30 GPa、0.28，折中结果如图6所示．

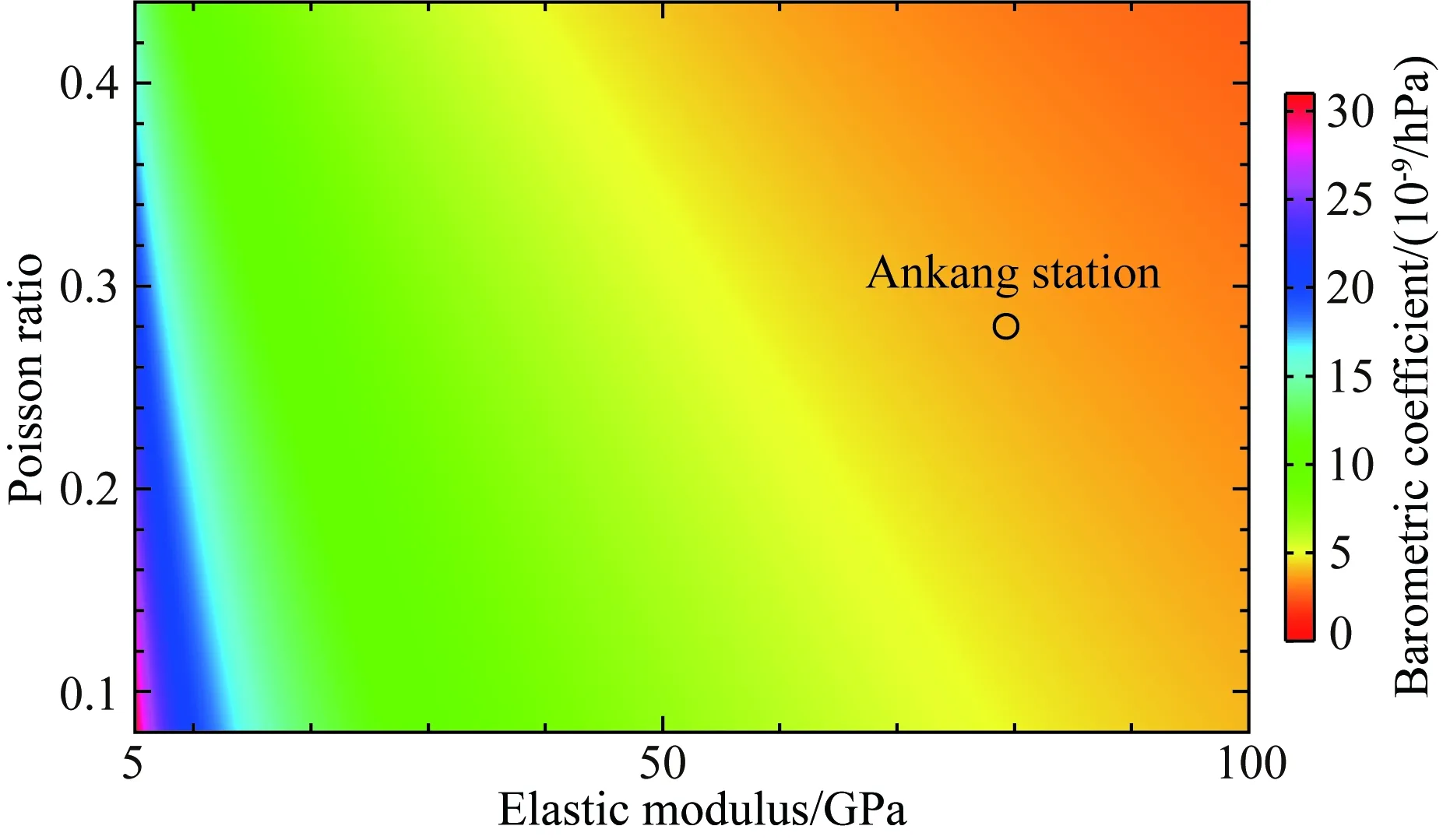
图6 安康台钻孔围岩力学参数的折中值，黑色圆圈表示最佳参数值Fig．6 Maximum barometric coefficient calculated at borehole depth 65.0 m (station Ankang) to illustrate trade-off between model parameters E3 (elastic modulus)and v3 (Poisson′s ratio)． The black open circle represents the best parameters for the model according to the surrounding rock type of the borehole

在此基础上，利用式(6)、(7)还能计算全频带的理论气压系数．需要说明的是，在求解周期<12 h的气压系数时，气压波的传播速度统一取典型值4.5 m·s-1(张凌空和牛安福，2019)，其主要目的是为了进一步简化高频气压响应问题．对比各频带实测和理论气压系数(图7)，可以发现绝大部分频点的偏差较为明显，而高度吻合的频点极少．这主要是由于真实大气的波动非常复杂，不同周期气压和体应变的相干性也不尽一致(图3a)；加之，体应变还会受到其他物理源的干扰．但就总体拟合度而言，理论值和实测值大致相符(除日波和部分频段外)，这表明估算值基本符合实况；而从另一方面来看，也反映出该台的气压响应机制并不单一．

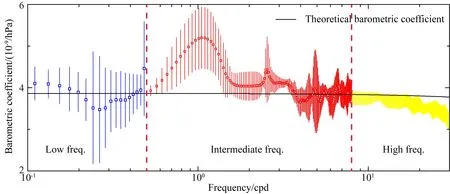
图7 安康台不同频带理论和实测气压系数的对比蓝色、红色和黄色空心方格分别为低、中和高频带同一频点的实测均值，与之对应的竖线表示95%的置信区间．Fig.7 Comparison of the theoretical and observed barometric coefficients in the low-， intermediate-， and high-frequency band， respectively． The theoretical barometric coefficients are marked by the black traceThe red dashed vertical lines mark the 0.5 cpd (left) and 8 cpd (right)，respectively． The blue， red， and yellow open squares with vertical lines indicate the average observed values with the 95% confidence interval in the three frequency band， respectively．

综上可见，基于双衬套理论的线弹性介质模型，所给出的理论气压频响虽与实况不尽一致，但大体相当，初步结果尚令人满意．由此可见，利用低频带气压系数来推定钻孔围岩力学参数的方法，行之而有效；同时，也在一定程度上佐证了该模型的局限性．

6 讨论

6.1 高频气压响应的可靠性

如前文所述，高频带气压和体应变的整体相干性不如低频带，且随机性偏大．那么高频带气压响应的传递函数是否可靠有效？为此，我们随机生成两组服从正态分布的“气压”和“体应变”数据，其长度与本文选取的实测数据一致，即1440×151个采样点．之后，依照前述高频带传递函数的计算方法，来分析这两组数据集的响应关系．

经过50次的反复测试，我们发现气压及其变异系数分别介于0.10～0.13×10-9/hPa，45.1%～59.5%之间，而本文所给出的平均气压系数最小值和平均变异系数的最大值分别为1.66×10-9/hPa、28.9%，可见二者均明显优于测试结果．不仅如此，从图4亦能看出高频带与其他频带的气压响应高度连续．综上两点，可以判定本文计算的高频带结果是合理可信的．

6.2 高频气压响应的影响因素

对于TJ-2型体应变观测系统，其高频气压响应主要是由孔深和气压周期等参量控制．张凌空等(2011)通过理论计算，指出当气压频率<～41 cpd时，孔深对气压系数的影响基本可以忽略．那么实况是否如此？另外，区域地形和气压系数的关系若何？有鉴于此，本文将各台σH和孔深分别与高、低频气压系数的平均变异系数进行了对比，结果如图8所示．

可以发现，除乾陵台外，其余各台高频带的变异系数均小于～11%，并随σH增大而缓慢上升，但低频带的变异系数与σH的相关性并不明显．其中一个值得注意的现象是，σH越大，高、低频带变异系数的差值愈明显(图8a)，说明地形地质结构较复杂的造山带区域，高频气压比低频的作用机制更加复杂多样．

一般来讲，钻孔越深受高频气压干扰的程度就会越小．结合表1和图8b，可以看出乾陵台的孔深最深，但其高频带的变异系数却最大，这可能是由该台周边黄土层的弹塑性力学特性所致．其他台高频带的变异系数和孔深则基本无关，可见，理论和实际结果大致相符(张凌空等，2011)．而低频带气压变异系数与孔深的关联性就更弱，这主要是因为各台孔深均远小于长周期气压的波长，所以可忽略孔深的影响．

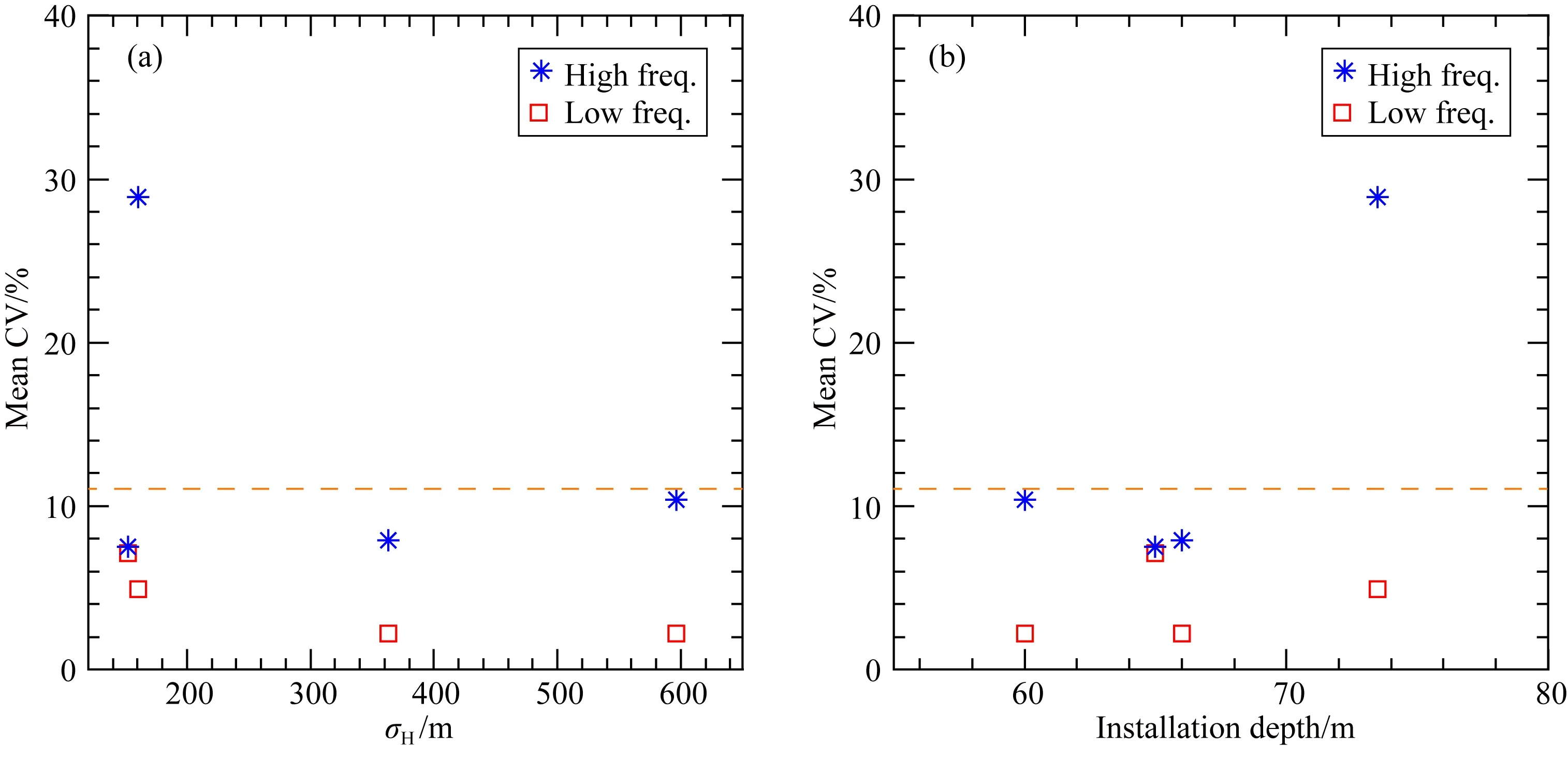
图8 各台高频气压系数的平均变异系数(蓝色星号)与区域地形高程标准差σH(a)和孔深(b)的相关性．其中，橙色虚线对应11%的变异系数Fig.8 The mean CV (coefficients of variation) of the barometric coefficients at high frequencies (blue asterisks) vary with the standard deviation of the regional topographic elevations (a) and the installation depths of borehole dilatometers (b) for the four stations， respectively． The orange horizontal dashed lines correspond to the 11% for mean CV

6.3 气压和固体潮差异响应分析

为进一步探讨体应变对气压和固体潮响应间的差异，本文特意选取了几乎不受气压影响的M2波的潮汐因子，并将其与低频带气压系数的平均值进行对比，具体结果如图9所示．一个有趣的现象是，西安和宁陕台虽同为花岗岩台基，但二者却似乎服从线性的反比例分布，即低频气压响应越好，M2波响应就越差，反之亦然．从已有的理论结果来看，泊松比v3与气压系数大致呈负相关(张凌空等，2011)，而潮汐因子又与E3负相关(Asai et al．，2009；李进武和邱泽华，2014)．所以，该现象可能主要是因二者v3不同所致(Furuya and Fukudome，1986)．

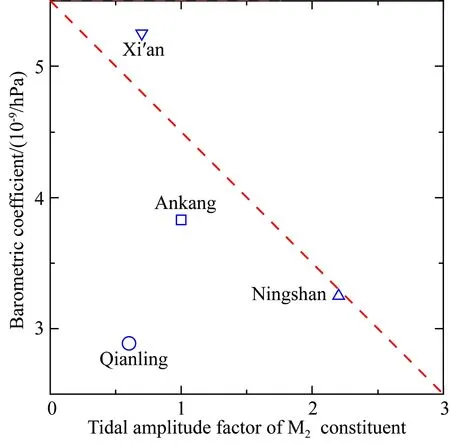
图9 各台低频带的平均气压系数与M2波潮汐因子对比Fig.9 Correlation diagram between the average barometric coefficients at low frequencies and the tidal amplitude factor of M2 constituent for the Ankang (square)， Ningshan (triangle)，Xi′an (inverse triangle)，and Qianling (circle) borehole dilatometer stations

7 结论

为考察不同频带体应变对气压和固体潮响应的全貌，本文以陕西地区4个体应变台为特例，并尝试采用传递函数对其进行了系统诊断；在此基础上，也初步探究了各台共性和个性响应背后的动力学机制，主要认识如下：

(1)体应变、气压和固体潮三者间的相干性差异明显，在0.1～30 cpd频带，各台体应变和气压整体上表现为强相干；在日波/半日波频段，体应变和固体潮的相干性较强；气压和固体潮则主要在S1和S2波处较高．

(2)各台低频带气压响应的稳定性最佳，高频带次之，中频带较差，造成这种差异响应的物理原因是能量较强的长周期气压波在低频带起了主导作用；而高频带气压和体应变的信噪比虽较低，但通过叠加传递函数仍可获得相对可靠的高频气压响应；中频带稳定性明显劣化的主因，是由于固体潮的强干扰．在相移方面，除日波等部分频段存在小幅超前现象外，其他频段均以滞后为主．平均而言，各频带的相位滞后都在9°以内，这说明实际地层介质具有一定的滞弹性效应．

(3)在全频带，若不考虑日波频段的影响，安康台的气压响应近线性平稳，其余3台的非线性频响特征较为明显，其中，宁陕和西安台的气压系数随频率增加而呈非线性衰减趋势．这也表明安康台钻孔的耦合度较高，区域地壳介质各向异性小，弹性性能良好，其他台则次之．安康台钻孔围岩的弹性模量和泊松比，可利用双衬套力学模型进行反演，结果分别为79.30 GPa、0.28．

(4)固体潮响应在半日波频段平稳收敛，而日波频段则相对发散，这主要是由于部分日波受到气象等因素的干扰；此外，传递函数和最小二乘法所提取的主要潮波参数具有较好的一致性．

(5)各台低频气压和固体潮响应间的关系有所不同，相比而言，西安台对前者的响应明显优于后者，宁陕台则反之，这可能是因为各台钻孔围岩的泊松比不同所致．

由于本文分析的台站数量较少，相关认识尚不全面．但从初步结果来看，基于双衬套钻孔的线弹性介质模型，还不足以刻画气压响应的非线性非平稳特性，该模型尚不具普适性．因此，今后还需提取更多体应变台的传递函数，进而为线弹性、孔弹性或弹塑性等动力学模型的合理构建和科学优化等，提供更为翔实可靠的实证依据．此外，加强对钻孔围岩力学参数、区域地壳弹性结构和水动力环境的勘查，也有益于传递函数的物理解释和理论模型的完善．

另外，山区复杂的地形动力学效应对潮汐和气压场的影响量若何？其引致传递函数的变异程度有多大？日波/半日波等潮汐频段对气压响应的影响量级如何？均是本研究尚未解决的细节问题．在后续的工作中，我们将会对这些问题进行更定量的探讨．

最后特别要强调的是，我国西部地区强震危险性较高，但区内的体应变台却并不密集，监测能力也有所不及(邱泽华，2014)．因此，如何借助数字信号处理或动力学模型等，来深刻探赜区内体应变信号中所潜藏的地震前兆等信息，是地震工作者所面临的巨大挑战．但今后无论如何都值得深入探索，这不仅对体应变观测的“去芜存菁”和“提质增效”等大有裨益；同时，也能促进西部地区地震预测预报等实际业务能力和潜力的提升．

致谢降水数据由中国气象科学数据共享服务网提供(http：∥data．cma．cn)，中国地震局地壳应力研究所邱泽华研究员、中国台湾中央研究院地球科学研究所Alexandre Canitano博士、美国地质调查局(USGS)Andrew J．Barbour博士和日本产业技术综合研究所北川有一(Yuichi Kitagawa)研究员等，就钻孔体应变对气压响应的机理问题，与作者进行了多次有益探讨，中国地震局地球物理研究所来贵娟博士在传递函数计算方面给予了指导；两位评审专家提出了诸多有益建议，对稿件质量的提升帮助很大，作者在此一并表示诚挚感谢．