横隔板对波形钢腹板组合梁翼缘有效宽度影响研究
2021-08-03吴启明董桔灿
吴启明 董桔灿
(深圳市市政设计研究院有限公司 广东深圳 518029)
0 引 言
波形钢腹板组合梁通常会设置较多的横隔板,以提高抗扭能力,并为体外预应力筋提供转向功能。横隔板对截面的翘曲变形具有约束作用,势必影响组合梁的剪力滞效应和翼缘有效宽度。为准确计算波形钢腹板组合梁翼缘有效宽度,有必要对横隔板带来的影响进行研究。
目前,即使包括传统混凝土箱梁在内,针对横隔板对翼缘有效宽度影响的研究不多。张洪斌等[1]基于有限元分析发现,横隔板的设置对单箱双室悬臂箱梁2个梁段的正应力分布有一定影响,剪力滞系数最大值可提高5%,对远离横隔板梁段的剪力滞效应基本无影响。波形钢腹板组合梁方面,易建强[2]对试验梁缩尺模型的有限元分析发现,横隔板能有效减弱其附近截面位置处顶、底板的剪力滞效应。朱世峰等[3]对三跨连续梁有限元分析发现,剪力滞系数随着箱梁内横隔板设置间距的减小而降低。然而卫星等[4]对中三跨连续梁有限元分析,却发现增设隔板不能减小剪力滞效应。陈曦[5]研究了横隔板数量对波形钢腹板曲线箱梁剪力滞的影响,并且发现横隔板的设置改变了沿桥纵向剪力滞效应的分布规律,在设计中应予以重视。
可见,横隔板对波形钢腹板组合梁剪力滞效应的影响还没有定论,需要从机理上开展进一步的研究。本文以30 m+50 m+30 m连续梁为对象,首先通过有限元法研究横隔板刚度对截面翘曲变形的影响,以及跨间横隔板对组合梁翼缘有效宽度的影响。其次,针对支点处横隔板,提出了在波形钢腹板组合梁剪力滞效应微分方程的基础上,通过引入广义位移函数边界条件,计算其对翼缘有效宽度影响的方法,并使用有限元方法验证了所提方法的准确性。
1 横隔板厚度对翼缘板翘曲变形约束能力的影响
研究对象为30 m+50 m+30 m连续梁,采用单箱单室截面,梁宽16.5 m,梁高2.5 m。翼缘板采用C50混凝土,材料弹性模量3.45×104MPa,泊松比0.2;钢腹板型号为《波形钢腹板组合梁桥技术标准》(CJJ/T 272-2017)[6]规定的1000型,厚度9 mm,采用Q345C钢材,材料弹性模量2.06×105MPa,泊松比0.31。图1为截面细部构造,图中单位为mm。图2为1000型波形钢腹板的构造。

图1 1/2截面细部构造
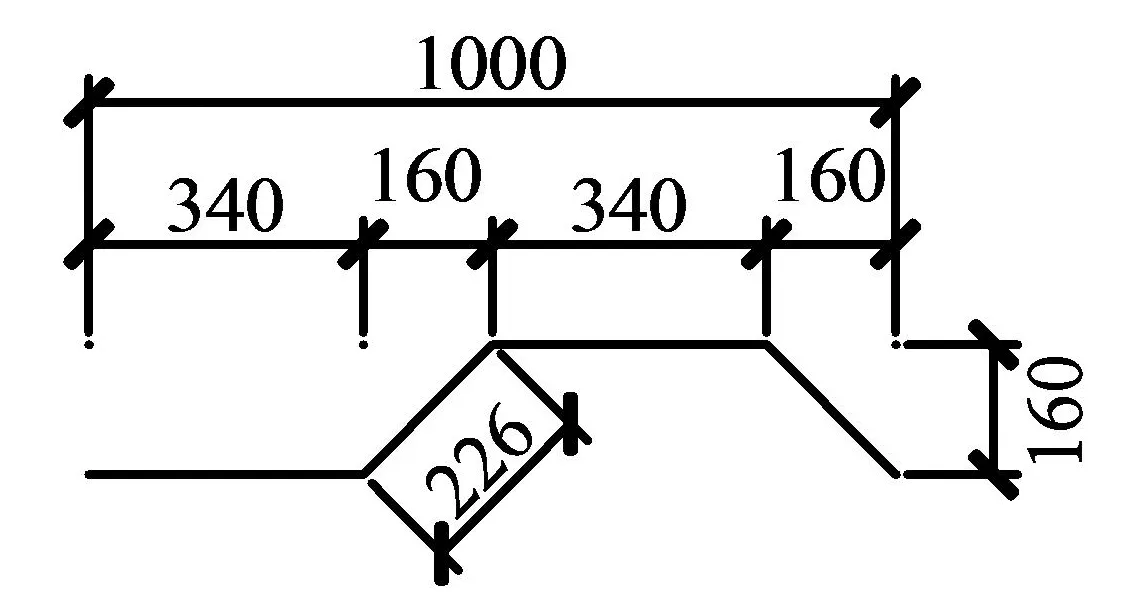
图2 1000型波形钢腹板构造
根据计算结果,在中跨距离中,支点4.5 m处剪力滞效应翘曲变形最大,因此于该位置添加横隔板,研究横隔板刚度对翼缘板翘曲变形约束能力的影响。横隔板的刚度取决于厚度,考虑 0.3 m、0.5 m、1.0 m、理想刚性横隔板、不设置横隔板共5种工况。其中理想刚性横隔板指板面外的刚度无穷大。
采用通用有限元软件ANSYS建立该连续梁的三维实体有限元模型进行分析。模型中,翼缘板、横隔板均采用SOLID95单元模拟,波形钢腹板采用SHELL63单元模拟。连续梁支座采用线约束的方式模拟。理想刚性横隔板通过将混凝土材料弹性模量放大106倍来近似考虑。荷载以均布线荷载的方式加到顶板与腹板交接位置。图3为有限元模型。图4为有限元分析得到的、组合梁在均布荷载作用下的翼缘板与横隔板接触位置的纵向位移结果。图中数据表明,随着厚度增加,横隔板对箱内顶板、底板翘曲变形的约束作用越强,当为理想刚性横隔板时,可完全限制,而悬臂板则无影响;横隔板厚度为0.3 m、0.5 m时,与不设置横隔板的工况相比相差不大,约束作用较弱,厚度为1.0 m时,约束作用较明显,可视为半刚性。

图3 有限元模型

图4 翼缘板纵向位移横向分布
中小跨径的桥梁工程中,跨间横隔板的厚度通常为0.3 m~0.4 m,可不考虑其对翼缘板翘曲变形的约束作用;支点位置的横隔板需要承当支座反力,厚度较大,通常可达1 m甚至2 m以上,可按刚性隔板考虑。
2 跨间横隔板对翼缘有效宽度的影响
采用文献[7]中的翼缘有效宽度系数定义方法:
(1)
式中,ρ1、ρ2、ρ3分别表示悬臂板、箱内顶板、底板的翼缘有效宽度系数。其余各符号含义如图5所示,图中b1、b2、b3分别为悬臂板、箱内顶板、底板的宽度;A1、A2、A3分别为扣除腹板宽度内和梗肋部分的翼缘板面积,t1、t2、t3为翼缘板的平均厚度;yb1、yb2、yb3为翼缘板与腹板或梗肋相交处的y坐标;σx为截面的正应力。
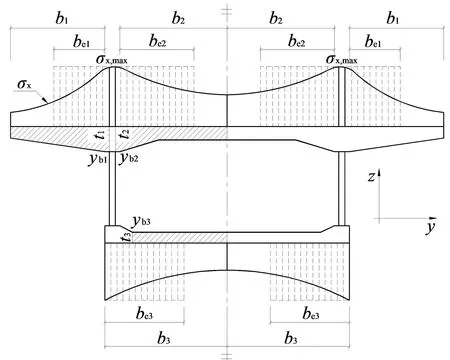
图5 翼缘有效宽度系数计算方法coefficient
图6为采用有限元分析得到的,组合梁在均布荷载作用下负弯矩区、正弯矩区的翼缘有效宽度系数对比结果。图中x=34.5 m为横隔板设置位置,图中数据可以看出,与其他位置相比,在横隔板设置位置附近,不同横隔板隔板设置工况下的翼缘有效宽度系数有一定差别。因此,跨间横隔板只影响其附近位置的翼缘有效宽度。
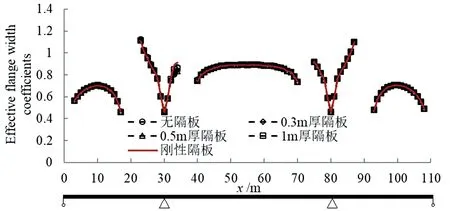
(a)ρ1
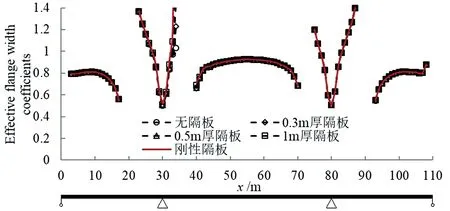
(a)ρ2
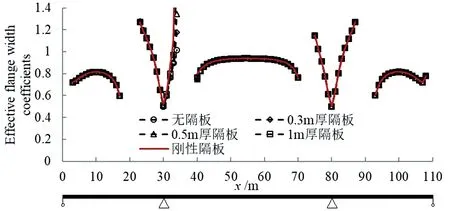
(a)ρ3
图7为临近横隔板位置、中支点位置、中跨跨中位置的翼缘有效宽度系数柱状图。图中在临近横隔板位置,不同横隔板设置工况下,ρ1为0.807~0.889,变化幅度0.082;ρ2为0.971~1.215,变化幅度0.244;ρ3为0.897~1.172,变化幅度0.275。因此,底板翼缘有效宽度受到横隔板的影响最大,其次为箱内顶板,最后为悬臂板。图7还可以看出,与不设置横隔板相比,翼缘有效宽度的变化随着横隔板刚度的增大而增大。而且,横隔板厚度在0.3 m、0.5 m时变化较小,因此可以认为当横隔板厚度不大于0.5 m时,可不考虑其影响。

(a)临近横隔板位置
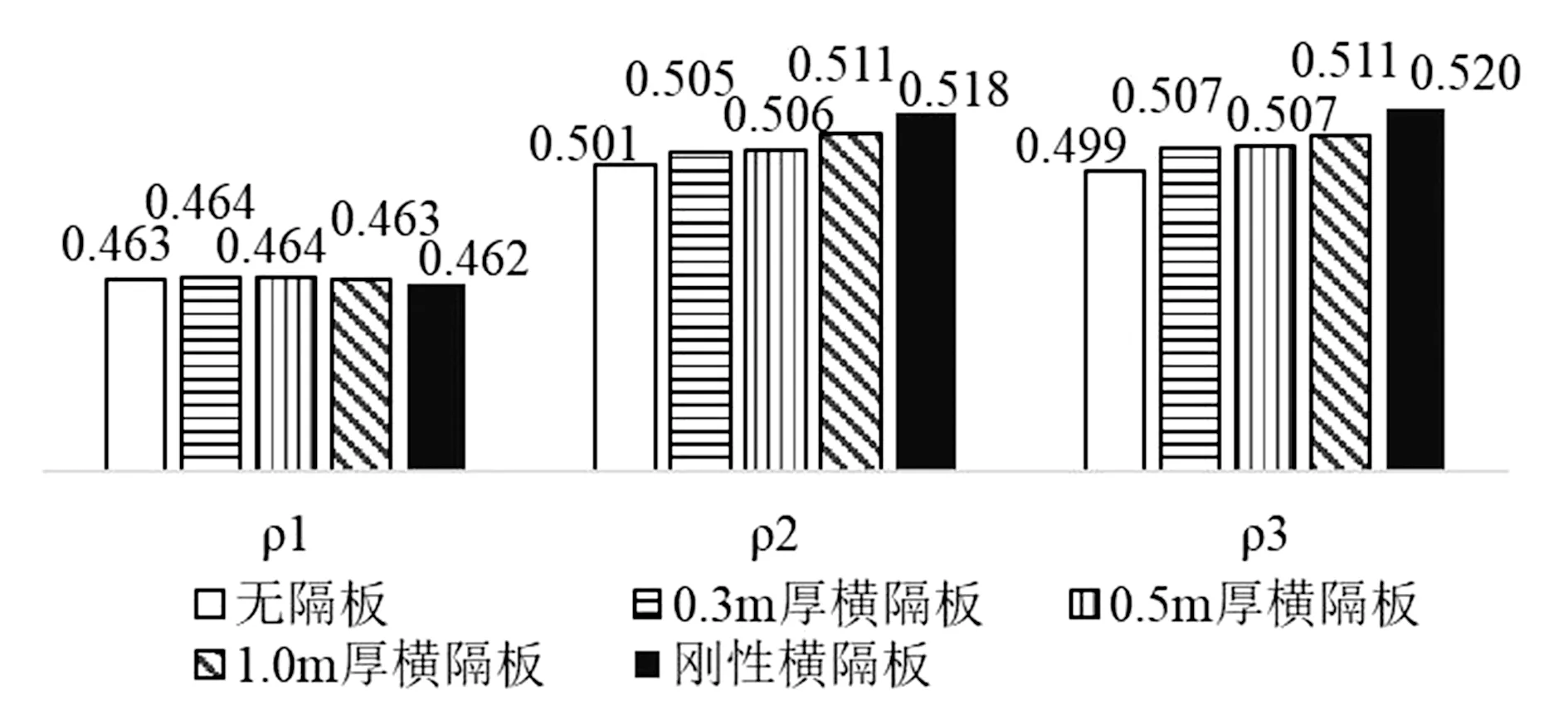
(b)中支点位置
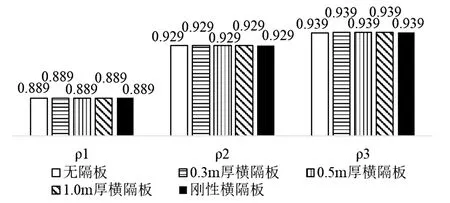
(c)中跨跨中位置图7 不同位置的翼缘有效宽度系数
3 支点横隔板的力学处理方法
支点横隔板厚度通常较大,可按刚性隔板考虑,即能够完全限制箱内顶板和底板的翘曲变形。为研究其对组合梁翼缘有效宽度的影响,在姜瑞娟等[8]建立的波形钢腹板组合梁剪力滞效应分析方法的基础上,通过在横隔板位置处,引入广义位移函数边界条件U2=U3=0来处理。
本例支点横隔板厚度1.0 m,可近似按刚性横隔板处理。为验证本文所提理论在处理支点横隔板方法上的正确性,采用4种方法对本例进行翼缘有效宽度计算和对比。4种方法分别为:有限元方法、本文所提方法、文献[8]方法、传统单广义位移函数分析方法。其中文献[8]方法与所提方法相比,没有考虑横隔板对广义位移函数的约束作用。传统单广义位移函数分析方法与所提方法相比,对悬臂板、箱内顶板、底板均采用同一个广义位移函数,且没有考虑横隔板对广义位移函数的约束作用。
图8给出了基于不同计算方法的翼缘有效宽度系数计算结果。图中数据表明,边支点附近区域每种方法有一定的差别,说明边支点横隔板的设置对其附近区域翼缘有效宽度存在影响,而不同的方法对这种影响的考虑不同。
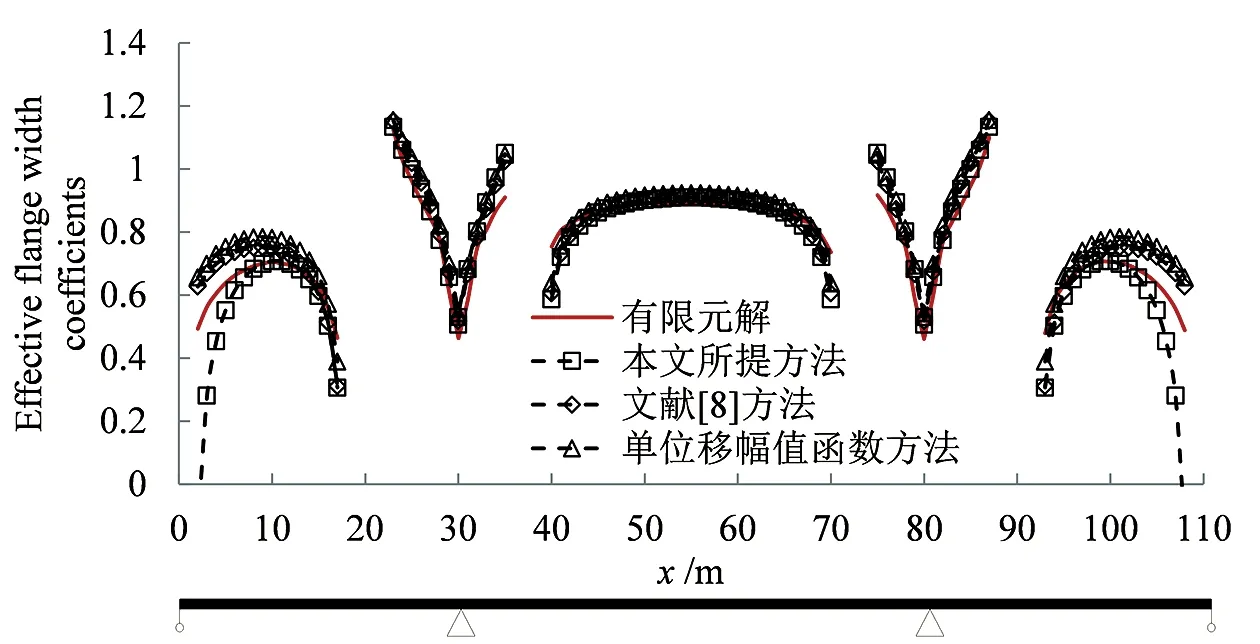
(a)ρ1
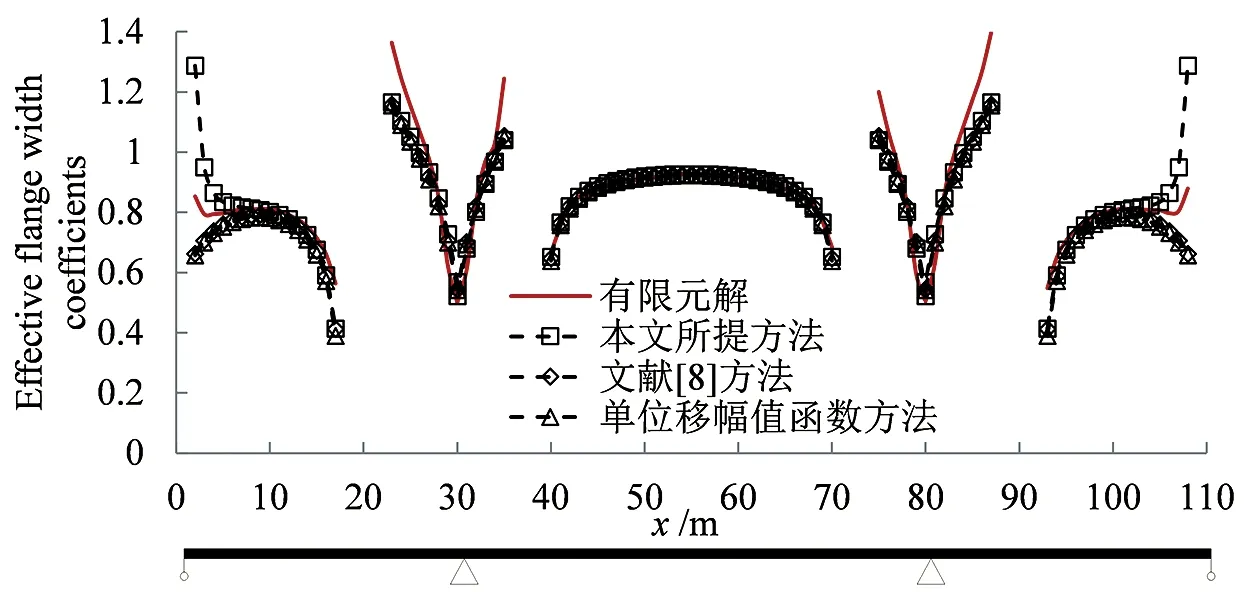
(a)ρ2
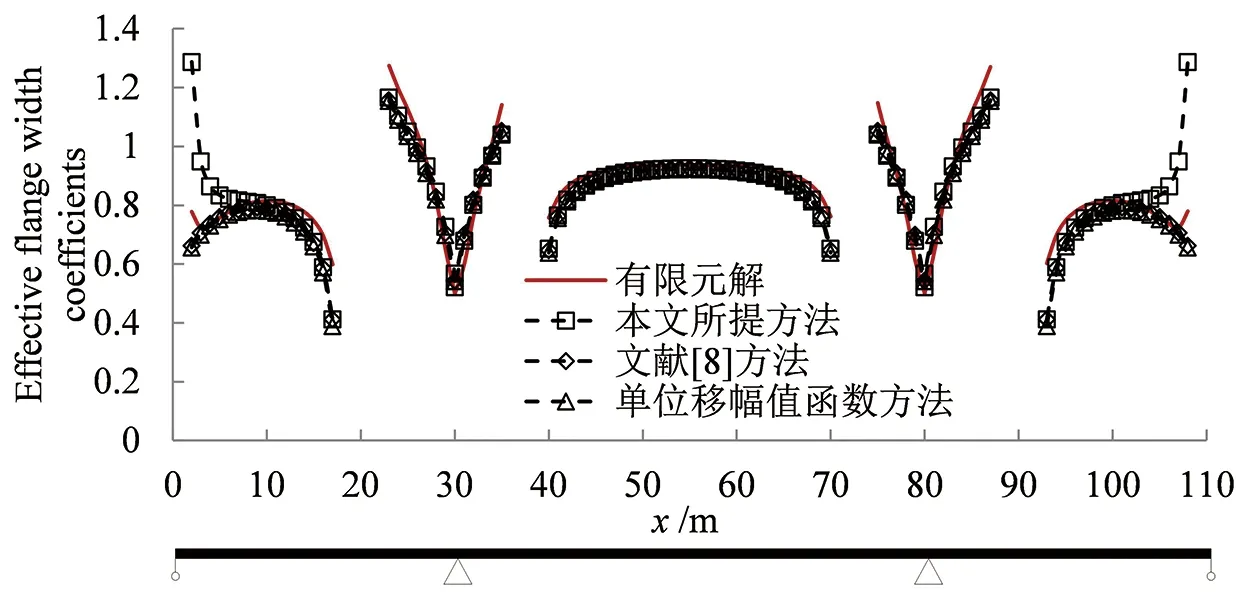
(a)ρ3 图8 不同方法下的翼缘有效宽度系数
图9为连续梁控制设计的3个关键位置的翼缘有效宽度系数柱状图。图中数据表明,本文所提方法与有限元解最接近,其次为文献[8]方法,最后为传统单广义位移函数分析方法。因此所提方法精度最高。而对于边跨跨中最大弯矩位置,受边支点横隔板的影响较大,所提方法的优势更明显,说明所提方法能更加准确地考虑横隔板对翼缘有效宽度的影响。

(a)边跨最大弯矩位置
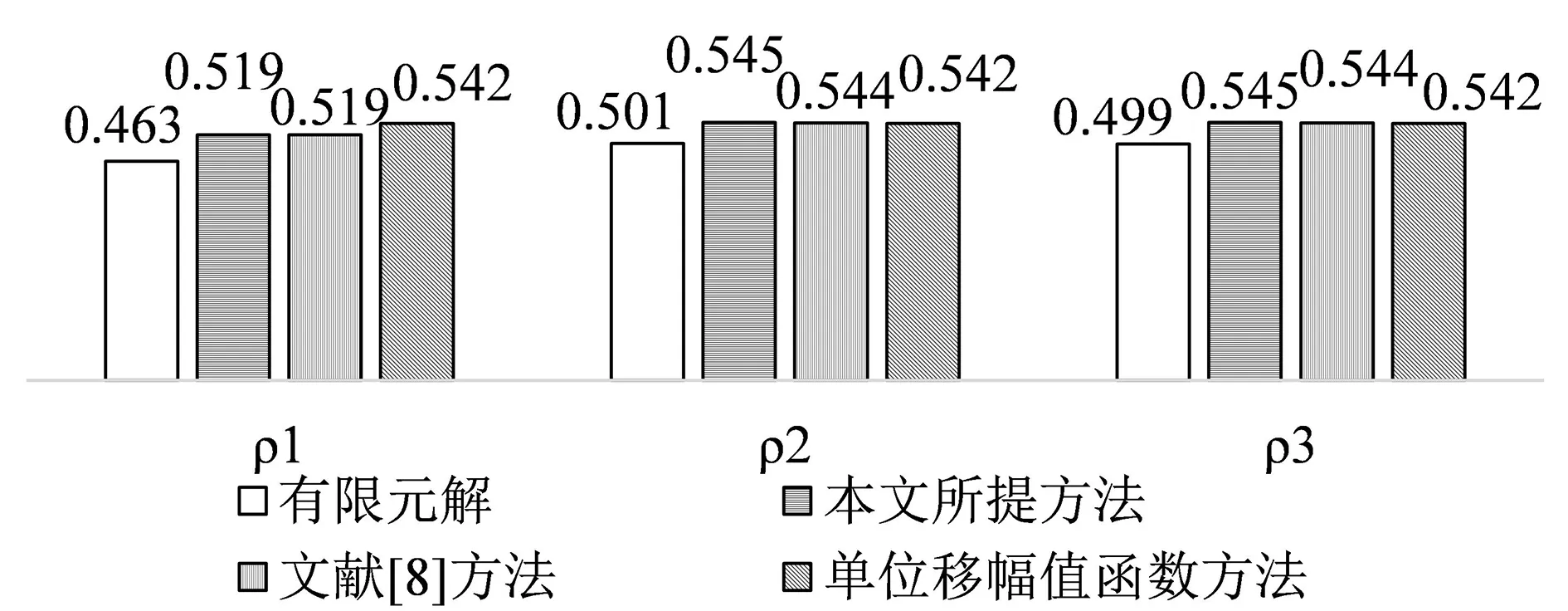
(b)中支点位置
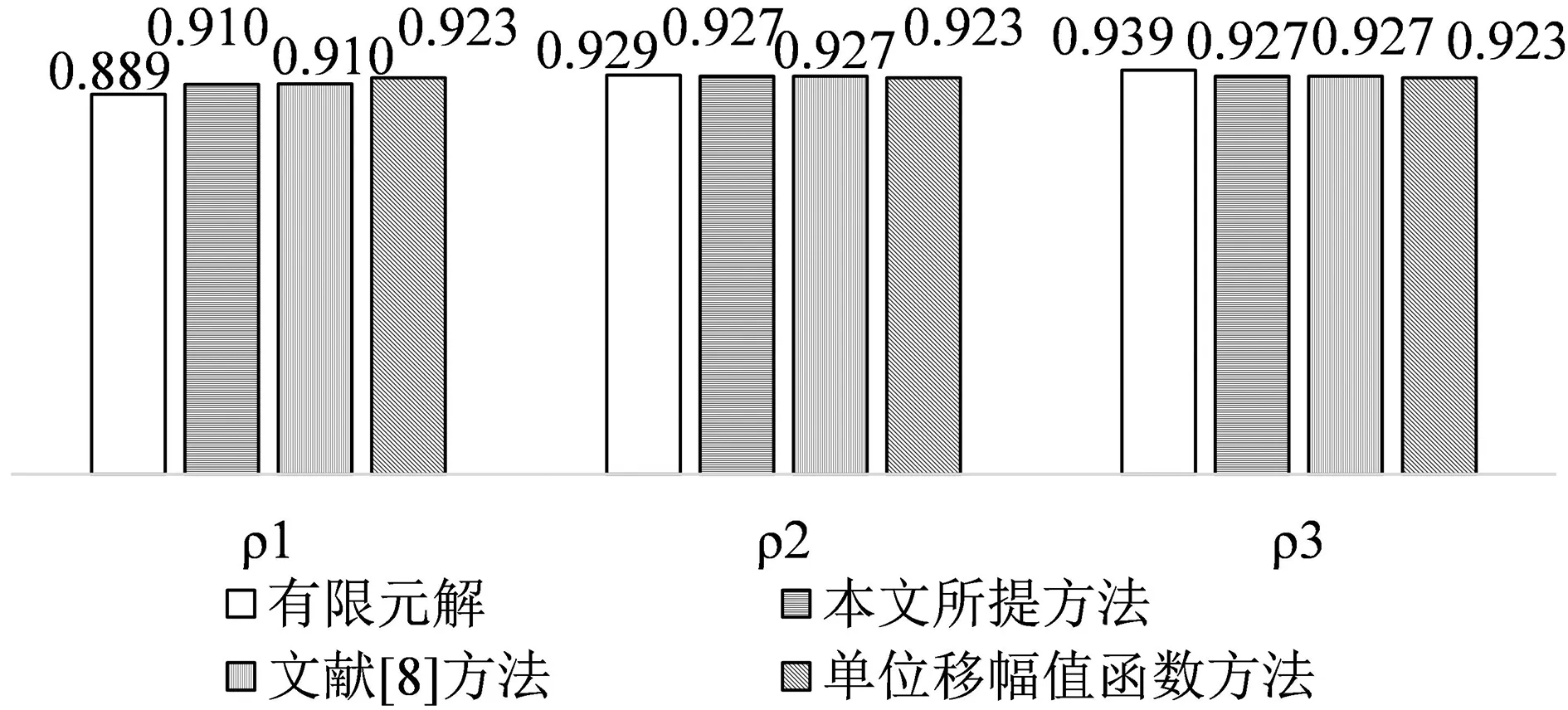
(c)中跨跨中位置图9 关键位置的翼缘有效宽度系数系数
4 结论
(1)横隔板位置处翼缘板纵向位移的计算结果表明,横隔板对箱内顶板、底板的纵向翘曲变形存在约束作用,且随着横隔板厚度的增加而加强,当横隔板厚度达1 m时为刚性横隔板处理。
(2)横隔板只影响其附近位置的翼缘有效宽度。对于通常情况下厚度较小的跨间横隔板,翼缘有效宽度计算时可不考虑其影响。
(3)厚度大的支点横隔板,可按刚性横隔板考虑。基于波形钢腹板组合梁剪力滞效应分析方法,可通过引入支点处的边界条件U2=U3=0来处理。有限元验证结果表明,该处理方法能提高翼缘有效宽度计算精度,尤其是边跨正弯矩区,效果较显著。
