一种求解图论中最大独立集问题的启发式算法

冯 云

(河北省药品医疗器械检验研究院，河北 石家庄 050081)

0 引言

最大独立集问题(Maximum Independent Set Problem)是图论中经典的组合优化问题，在生物信息学[1]，无线网络通信[2]，信息传输调度[3]以及社交网络分析[4]等领域有着非常广泛的实际应用，数十年来吸引了国内外大量学者进行研究。Carraghan[5]，Babel[6]，Östergård[7]，Li[8]等人研究了求解的精确算法(Exact Algorithms)，其核心都是基于分支界定策略(Branch and Bound Strategy)。分支界定的基本思想是对解的上界进行估计，当上界小于当前已知解时就放弃该分支的继续搜索，称作“剪枝”。后来有学者对分支界定策略进行了优化，利用动态规划、染色等方法加速剪枝的过程，提高精确算法的速度。尽管如此，在给定图中求解最大独立集仍是NP-hard问题[9]，当图的规模增大，求解该问题的时间复杂度越来越高，精确求解是不可能的，即使是超级计算机也无能为力。因此许多学者研究了启发式算法，启发式算法虽不能保证一定能够得到最优解，但在对于规模较大的最大独立集问题上具有极高的性价比。目前应用比较广泛的启发式算法有贪婪算法(Greedy Algorithm)[10-11]，局部搜索(Local Search)[12-13]和禁忌搜索(Tabu Search)[14]。贪婪算法通过一定的规则按顺序逐次扩充解的集合，直至顺序搜索结束，获得一个可行解。局部搜索对可行解的局部邻域进行搜索，来提高已知解的质量。禁忌搜索是一种改进的局部搜索算法，通过设立“禁忌列表”来避免在搜索过程中出现死循环，并且有助于跳出循环并开发新的搜索区域。本文综合了贪婪算法与禁忌搜索各自的特点，提出了一种启发式的最大独立集问题解法，并使用DIMACS基准中的实例进行了验证，取得了令人满意的效果。

1 最大独立集问题

考虑一个无向图G=(V,E),V={1,…,N}是图中的N个顶点(Vertex)，E⊆V×V是图中棱的集合，每条棱都连接着V中的2个顶点。每条棱所连接的2个顶点被称作是相邻的，或者互为“邻居”。如果V的一个子集I中任意2个顶点都是不相邻的，那么I被称作一个独立集，|I|是子集I中顶点的数量。如果I不被任何其他独立集I包含，那么I被称作一个极大独立集(Maximal Independent Set)，如果|I|是图G的所有极大独立集中最大的，那么I被称作最大独立集(Maximum Independent Set)。最大独立集问题就是在一个给定图G中寻找G的最大独立集。

用N维向量X=(x1,x2,x3…xN)表示G的任意子集S，xi∈{0,1}，其中xi=0表示顶点vi不在S中，xi=1表示顶点vi在S中。所以求解最大独立集问题也可以转化成一个整数规划问题：

s.t. xi+xj≤1, for all(i,j)∈E

xi∈{0,1}, i∈V

2 算法介绍

2.1 三个概念

(1)点的邻居：在无向图G=(V,E)中，V是顶点的集合，E是棱的集合，对于任意一个点vi，vi的邻居是N(vi)={vi∈V,(i,j)∈E}，每一条棱连接的2个点互为邻居。

(2)点的度d(vi)：表示vi的邻居的个数，即d(vi)=|N(vi)|

(3)点的支撑s(vi)：表示vi所有邻居的度之和，即s(vi)=∑vj∈N(vi)d(vj)

如图1所示，所有顶点和棱组成了一个无向图，N(C)={A,B,D,E}，d(C)=3，s(C)=d(A)+d(B)+d(D)+d(E)=12，{A,H}是一个独立集，{A,E,H}是极大独立集，{B,D,E,H}是最大独立集。

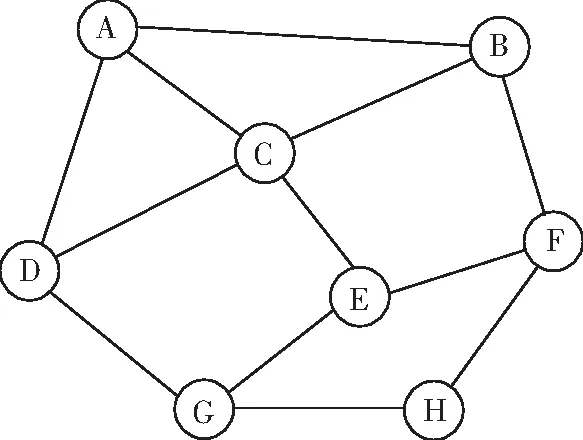
图1 一个无向图

2.2 算法描述

有研究表明，使用启发式算法求解最大独立集问题时，把多种算法结合使用所呈现的性能要好于单纯使用一种算法时的性能[15]。如引言中所述，当贪婪算法运行结束，找到一个极大独立集后，搜索停止，所找到的极大独立集满足最大独立集条件的概率非常低。而局部搜索仅能够找到局部最优值，为了提高求解的质量，本文结合贪婪算法与禁忌搜索，提出一种新的方法。以下给出求解图G中最大独立集的算法。N维方阵A=(aij),i,j∈(1,2,…,N)，用来描述无向图G，A称作邻接矩阵，为一个对称矩阵，aij=aji，对角线元素aii=0，aij=1表示vi与vj通过棱相连，aij=0表示vi与vj没有棱直接相连。本算法的输入变量为邻接矩阵A。本算法的输出是V的一个子集I，用N维向量X表示，X的第i个元素为1表示点vi在I中，称作点vi被选择到最大独立集的解之中；第i个元素为0则反之。

本算法(RI-DS-TS)分为3部分：随机初始化(Random Initialization)，基于点的度(Degree)与支撑(Support)的顶点挑选，基于禁忌搜索(Tabu Search)的独立集优化。

(1)本算法是启发式的，每次运算得到的一个可行解，并不能保证是最优解，而且该可行解与最优解的偏离程度是无法估计的。所以本算法需要多次重复，以期获得可接受时间范围内的最优解。由于图的产生本身具有随机性，重复求解的过程需要尽可能多的搜寻潜在的可行解。一旦确定了1个起始点后，所有可能的可行解数量十分有限(会在下一步具体描述)，为了尽可能多的增加求解过程的随机性，在选择点的时候，前m个点是等概率随机选择的。根据算法调试过程中的经验，m取值为图G中点数量的1/500(向上取整)。

(2)本部分思想来源于贪婪算法，研究的核心内容是如何制定合理可行的顶点挑选规则和顺序。本部分的顶点选择是不断迭代进行的，每次只选择一个点。在迭代的过程中，如果点vi被选择，那么vi的所有邻居N(vi)都要被放弃，vi和N(vi)在邻接矩阵A中所对应的行和列都要被删除。所以，本部分的中心思想就是在选择1个点的同时，尽可能少的放弃其他点，也就是每次都选择度d最小的点。如果有多于1个点的d相同，则选择其中支撑s最大的点。因为点vi的邻居N(vi)被放弃后，支撑s(vi)表示之后有可能被选中的点的数量。如果有多于1个点同时满足d最小和s最大，那么在这些点中随机选择1个。点的选择迭代进行，直到邻接矩阵A为空时结束，所有被选中的点组成一个极大独立集。当起始点被确定后，只有遇到多于1个点同时满足d最小和s最大时，才有可能产生多个不同的可行解。所以在第1步中，为了增加获得的可行解的数量，前m个起始点的选择是完全随机的。

(3)前2步后获得的是一个极大独立集I，并不能保证是“最大”，因此第3步再进行局部的禁忌搜索。禁忌搜索有2种操作，交换SWAP与增加ADD。增加操作是指，当在I的补集中存在1个点vi与I中的任意一个点都没有棱相连时，将点vi增加到I中，增加操作的候选集是所有有可能进行增加操作的点的集合。交换操作是指，当I的补集中存在1个点vi与I中除了1个点vj之外的所有点vk∈I,(k≠j)都没有棱相连时，将点vi与vj交换，交换操作的候选集是所有有可能进行交换操作的点的集合。每次交换操作后都要更新“禁忌集”，禁忌集内的元素在步操作之内不允许再次被增加或者交换至I中，这样保证了算法不会陷入局部解中无法跳出，本算法中t取7。增加操作可以使独立集中点的个数增加，交换操作不改变独立集中点的个数，但是有可能带来新的可行解。每次操作时，如果增加操作的候选集不为空，则进行增加操作，否则进行交换操作。第3步中首先要限定操作次数T，如果超过次操作后仍然没有更好的结果，则停止搜索，返回第1步。如果在T次之内独立集中点的数量增加，则将T清零，继续搜索。本算法中T取5000。在操作的过程中，如果增加操作和交换操作的候选集同时为空，也停止搜索。

3 仿真结果

文献[17]提出了一种并行求解算法，也使用了DIMACS基准图来测试算法效果。本文使用提出的算法RI-DS-TS分别求解了DIMACS库中的实例，将求解结果与文献[17]提出的MPICE-LS算法以及DIMACS实例的精确解或者目前的已知最优解做了对比。本文对每个实例，限定的算法运行时间为15min，运行环境为Inter®CoreTMi5-2430M,2.30GHz,8GB RAN,结果表明，除keller6外，本文所提出的算法RI-DS-TS均达到了文献[18]中算法求出的最大独立集大小。另外，对于文献[17]未验证的其他大多数实例，本文所提出的算法RI-DS-TS几乎全部能够达到已知的最优解，包括其中顶点数和棱密度很大的情况，而且对大部分实例RI-DS-TS算法运行时间均在数秒之内。但是当运行时间达到15min后，仍然有若干实例无法获得最优解。文献[18]从精确算法的角度，对比了不同算法对DIMACS中顶点数量为200的实例的处理效果，算法的执行时间随着棱的数量呈指数趋势上升，还指出当棱密度一定时，算法的执行时间随着顶点的数量也呈上升趋势。本文中未能获得最优解的这些实例均为顶点数超过4000或棱密度大于0.8的情况。图的顶点数和棱密度越大，邻接矩阵的维度会越大，非零元素会越多，导致了算法运行变慢。但是仍能看到，对于这些情况，本算法得到的结果已经非常接近，甚至一些棱密度超过0.8的实例已经达到了目前的最优解。

4 结论

研究提出了一种启发式求解图论中的最大独立集问题的算法RI-DS-TS，本算法综合了贪婪算法与禁忌搜索的思想，提出一种用于贪婪算法的挑选顺序，以图中顶点的度和支撑作为贪婪算法的选择策略，并通过禁忌搜索保证算法能够从局部最优解中跳出，作为次优解的优化方法。另外，为克服贪婪算法得到解数量有限的问题，保证重复求解过程中尽可能多的搜索潜在的可行解，RI-DS-TS算法还提出从随机起点开始运行贪婪算法。RI-DS-TS算法使用DIMACS基准图中的实例进行了验证，在76个实例的求解中，共70个实例都得到了理论最优解或目前已知的最优解。对于顶点数和密度都较大的实例，求出的解也非常接近最优解。所以本文提出的算法在考虑时间和计算成本的条件下，对于求解最大独立集问题效果十分理想。