弹性地基上Euler-Bernoulli梁的临界荷载计算
2021-08-02卢港伟葛仁余马国强刘小双余本源
卢港伟,葛仁余,夏 雨,马国强,刘小双,余本源
(安徽工程大学 建筑工程学院,安徽 芜湖 241000)
有关非均匀和轴向功能梯度(FG)梁的屈曲问题已在文献中进行了论述,然而,精确的解析解只存在于荷载和抗弯刚度分布的某些特殊情况,在一般弯曲刚度分布的情况下获得梁的正确解,应采用更多的数值方法。目前,国内外计算梁的屈曲临界荷载的文献较多,Eisenberger给出了不同刚度和荷载分布的非均匀梁、柱的屈曲实例,研究关于级数展开的高精度结果经常用于不同数值方法的比较和讨论。集中荷载作用下非均匀和轴向FG梁屈曲问题的数值解在许多论文中得到了广泛研究,Sapountzakis等发展了用于任意变截面组合Euler-Bernoulli梁弹性屈曲分析的边界元方法。Coskun等将变分迭代法应用于变截面欧拉梁临界屈曲荷载的确定问题。文献[9]将边界条件转换为一种简便的形式,避免了刚度系数矩阵的无穷大值问题,研究了轴向功能梯度变截面弹性地基梁的稳定性问题。文献[10]采用局部微分求积法研究了带有弹性约束的轴向功能梯度变截面桩稳定性问题。文献[11]采用一种低维数学模型,该模型能够计算均匀和非均匀的功能梯度桩沿轴线方向上的屈曲载荷。文献[12]利用优化的瑞利商和Timoshenko商解决了一些工程振动和屈曲稳定性问题。文献[13]给出了各种边界条件下,变轴力加载的变截面桩屈曲临界荷载的精确解。文献[14]提出了一种精确计算任意轴向不均匀梁的临界屈曲载荷的新方法,将变系数控制方程转化为线性代数方程,获得临界屈曲载荷。文献[15-16]采用微分求积法(DQM)分别研究了功能梯度Timoshenko梁的稳定性和弯曲变形问题。总之,数值方法是研究轴向功能梯度梁振动和稳定性问题的主要手段。
研究提出采用微分求积法求解弹性地基上功能梯度Euler-Bernoulli梁的屈曲临界荷载问题。基于Euler-Bernoulli梁理论建立了求解弹性地基上功能梯度Euler-Bernoulli梁屈曲临界荷载的变系数微分方程,运用微分求积法理论,将该变系数常微分方程的特征值问题转化为一组线性代数方程组的特征值问题,再由QR法可一次性地获得弹性地基梁的屈曲临界荷载。
1 计算模型
1.1 Euler-Bernoulli梁稳定性的基本理论
弹性地基上功能梯度Euler-Bernoulli梁如图1所示。考虑弹性地基上长度为l
且材料性能和截面面积沿轴向x
任意连续变化的Euler-Bernoulli梁,其挠度设为w
(x
,t
)。假设材料的弹性模量为E
(x
),材料的密度为ρ
(x
),截面面积为A
(x
),截面转动惯量为I
(x
),它们均为x
的函数,即E
(x
)=E
f
(x
),ρ
(x
)=ρ
f
(x
),I
(x
)=I
f
(x
),A
(x
)=A
f
(x
)。其中,E
、ρ
、A
、I
分别对应于轴向功能梯度梁在左端边界x
=0位置材料的弹性模量、密度、截面积和截面惯性矩;C
为地基弹性系数;设轴向力P
>0为压力,P
<0为拉力,则荷载P
作用下的功能梯度材料弹性地基Euler-Bernoulli梁的自由振动方程为: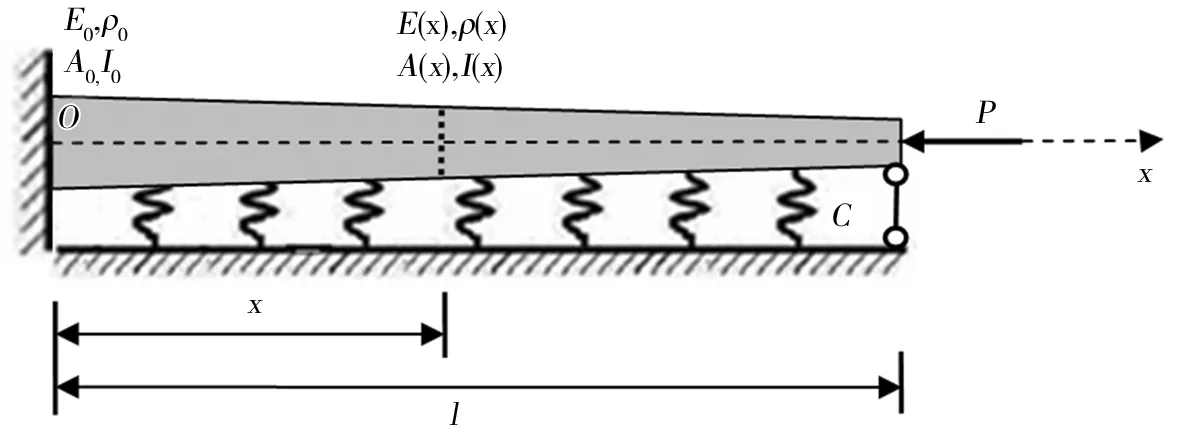
图1 弹性地基上功能梯度Euler-Bernoulli梁
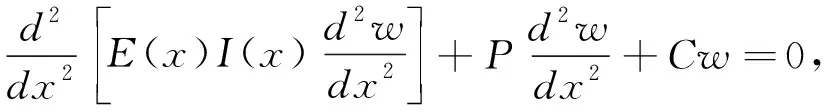
(1)
研究主要考虑梁的谐波振动问题,则有
w
(x
,t
)=W
(x
)sinωt
,(2)
式中,ω
为振动角频率;t
为时间;w
(x
,t
)为挠度;W
(x
)为振型函数。将式(2)代入式(1),可得轴向功能梯度Euler-Bernoulli梁在轴向力P
作用下的振动方程为: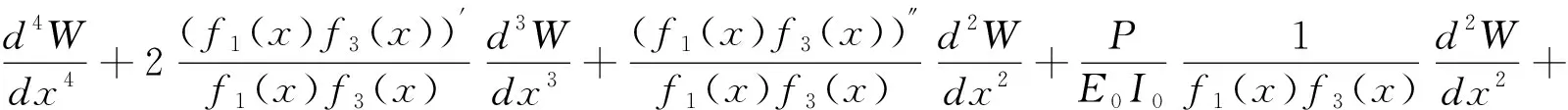
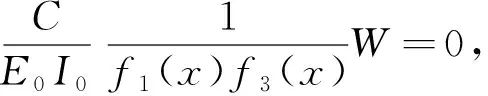
(3)
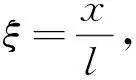
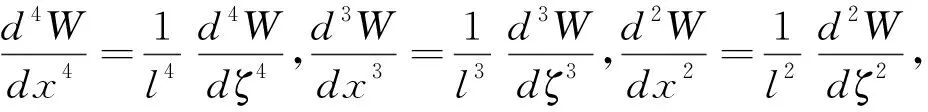
(4)
将式(4)代入式(3),可得关于轴向功能梯度Euler-Bernoulli梁临界屈曲荷载λ
特征值的控制方程为: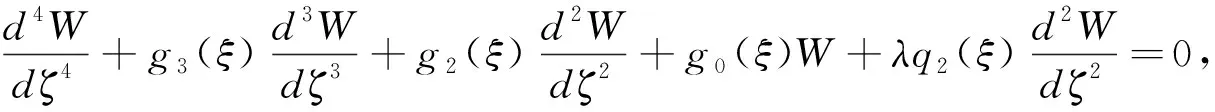
(5)
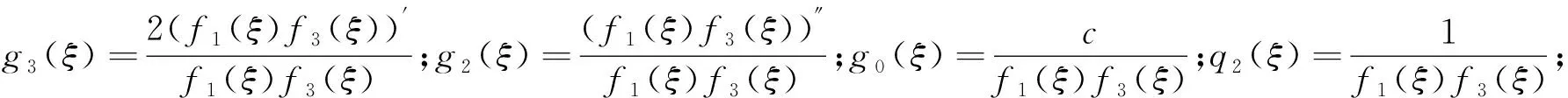
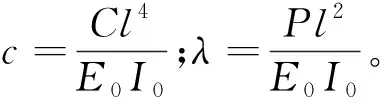
1.2 Euler-Bernoulli梁的边界条件
Euler-Bernoulli梁的转角θ
,弯矩M
和剪力T
分别为: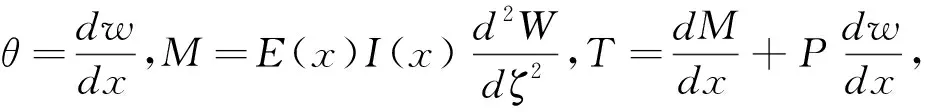
(6)
简支-简支梁(H-H)的边界条件为:θ
=0和M
=0,W
(0)=0,W
(0)=0;W
(1)=0,W
(1)=0,(7a)
固端-固端梁(C-C)的边界条件为:w
=0和θ
=0,W
(0)=0,W
(0)=0;W
(1)=0,W
(1)=0,(7b)
固端-简支梁(C-H)的边界条件为:w
=0和θ
=0、θ
=0和M
=0,W
(0)=0,W
(0)=0;W
(1)=0,W
(1)=0。(7c)
因此,弹性地基上Euler-Bernoulli梁临界屈曲荷载的计算可以转化为在边界条件式(7)下,常微分方程式(5)的特征值问题,研究采用微分求积法对此展开数值分析。
1.3 微分求积法分析
微分求积法的本质是把函数在给定的离散点上的各阶导数值,近似地用全域上所有网点处的函数值的加权和来表示。弹性地基上功能梯度Euler-Bernoulli梁的计算域为0≤ξ
≤1,离散单元数为n
,离散节点数为n
+1,离散节点的分布采用切比雪夫多项式的根和等比数列两种非均匀变步长布点方式。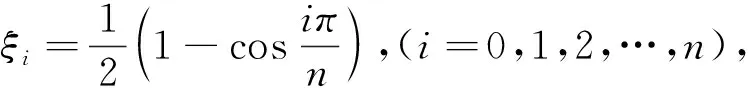
(8a)
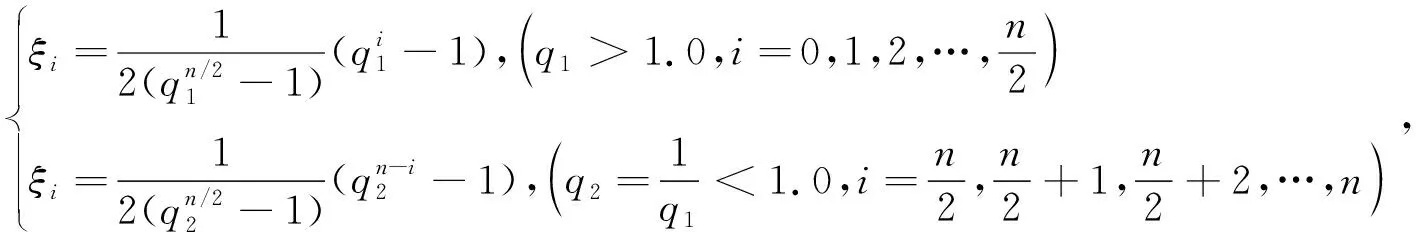
(8b)
根据微分求积规则,每个离散节点处对应的函数导数为:
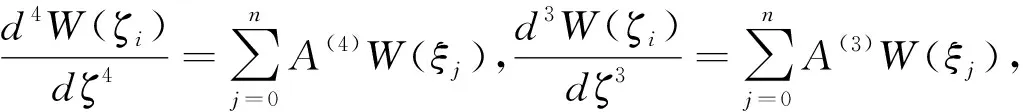
(9a)
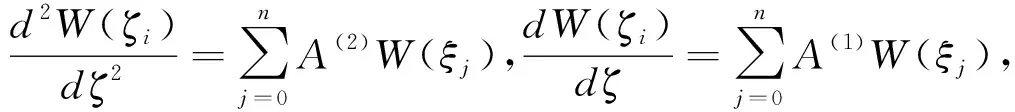
(9b)
这里,权系数的定义为:
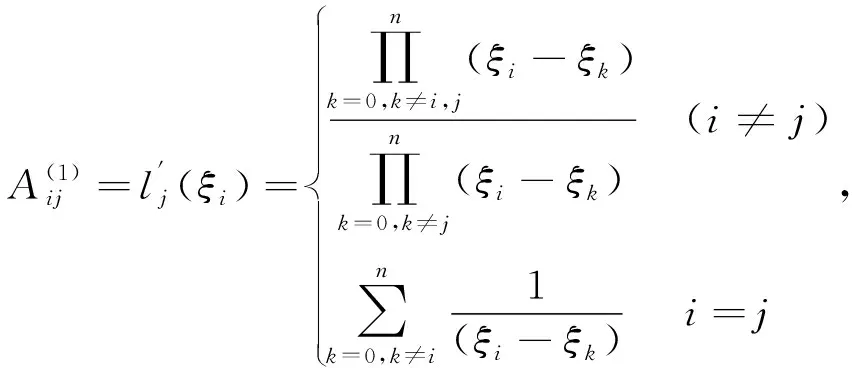
(10)
其中,权系数矩阵A
()的各阶导数之间的关系为:A
(+1)=A
A
()=A
()A
,(r
≥1),(11)
令r
=0时,权系数矩阵A
为单位矩阵I
,则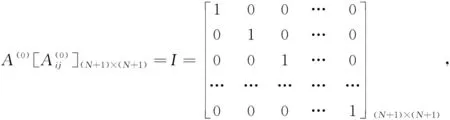
(12)
将式(11)代入控制方程式(5)和不同边界条件式(7),得到相应网格节点的微分求积近似离散为:
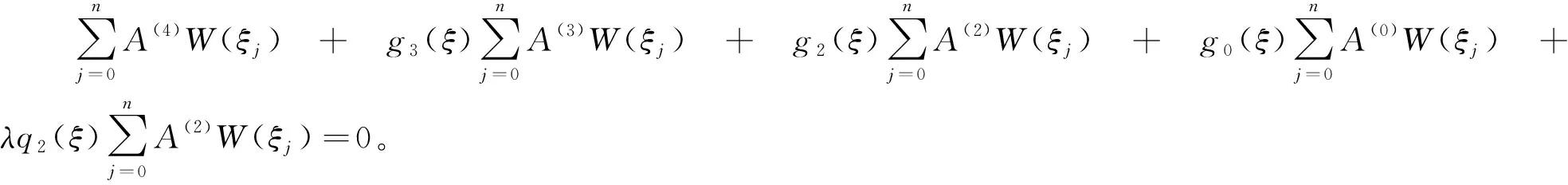
(13)
不失一般性,以两端简支梁(H-H)情况为例进行讨论。将式(11)代入式(7a),得
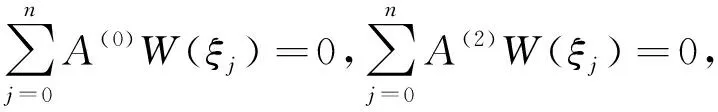
(14a)
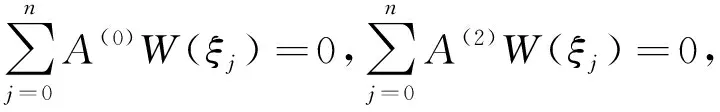
(14b)
至此,联立式(13)和式(14),采用QR法求解一般广义代数特征方程组,可得到在边界条件H-H下,弹性地基上功能梯度Euler-Bernoulli梁的屈曲临界荷载,其他边界条件可类似获解。
2 算例分析
对于长度为l
的轴向功能梯度变截面Euler-Bernoulli梁,给出式(15a)、式(15b)、式(15c)三种情形的抗弯刚度EI
(x
):EI
(x
)=E
I
(1+x
),(15a)
EI
(x
)=E
I
(1+x
),(15b)
EI
(x
)=E
I
(1+x
),(15c)
这里,梁抗弯刚度沿轴向呈多项式函数变化,即EI
(x
)=E
I
(1+x
),(k
=1,2,3)。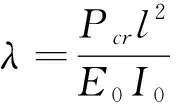

表1 梁的无量纲屈曲临界荷载值(EI(x)=E0I0(1+x);c=0;n=32)

表2 梁的无量纲屈曲临界荷载值(EI(x)=E0I0(1+x)2;c=0;n=32)
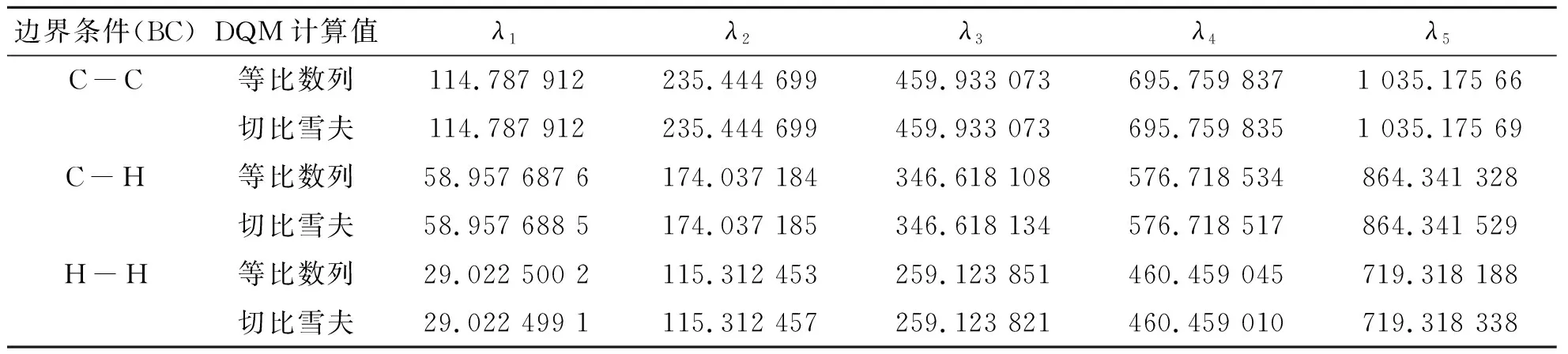
表3 梁的无量纲屈曲临界荷载值(EI(x)=E0I0(1+x)3;c=0;n=32)
当k
=2,即抗弯刚度EI
(x
)=E
I
(1+x
)时,考虑地基的影响,即c
≠0,运用微分求积法求解功能梯度Euler-Bernoulli梁临界荷载值,地基弹性系数分别取c
=25、50、100,弹性地基梁的临界荷载如表4所示。研究计算结果与文献[9-10]完全吻合;不考虑地基的影响,即c
=0,运用微分求积法求解功能梯度变截面Euler-Bernoulli梁临界荷载值,功能梯度Euler-Bernoulli梁的前5阶临界荷载如表5所示。微分求积法计算值与文献[9]和文献[11]结果完全吻合,再次证明了微分求积法求解弹性地基上功能梯度Euler-Bernoulli梁临界荷载的精确性。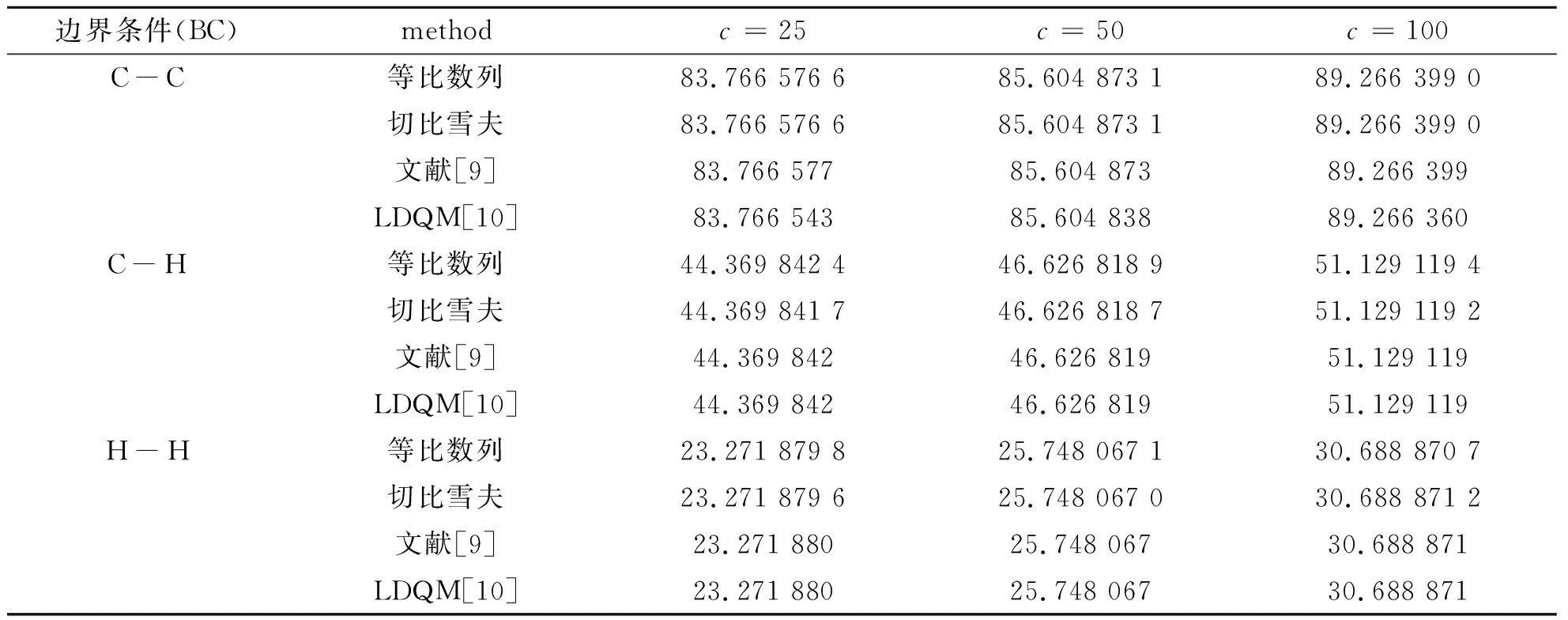
表4 梁的无量纲屈曲临界荷载值(EI(x)=E0I0(1+x)2;c≠0;n=32)
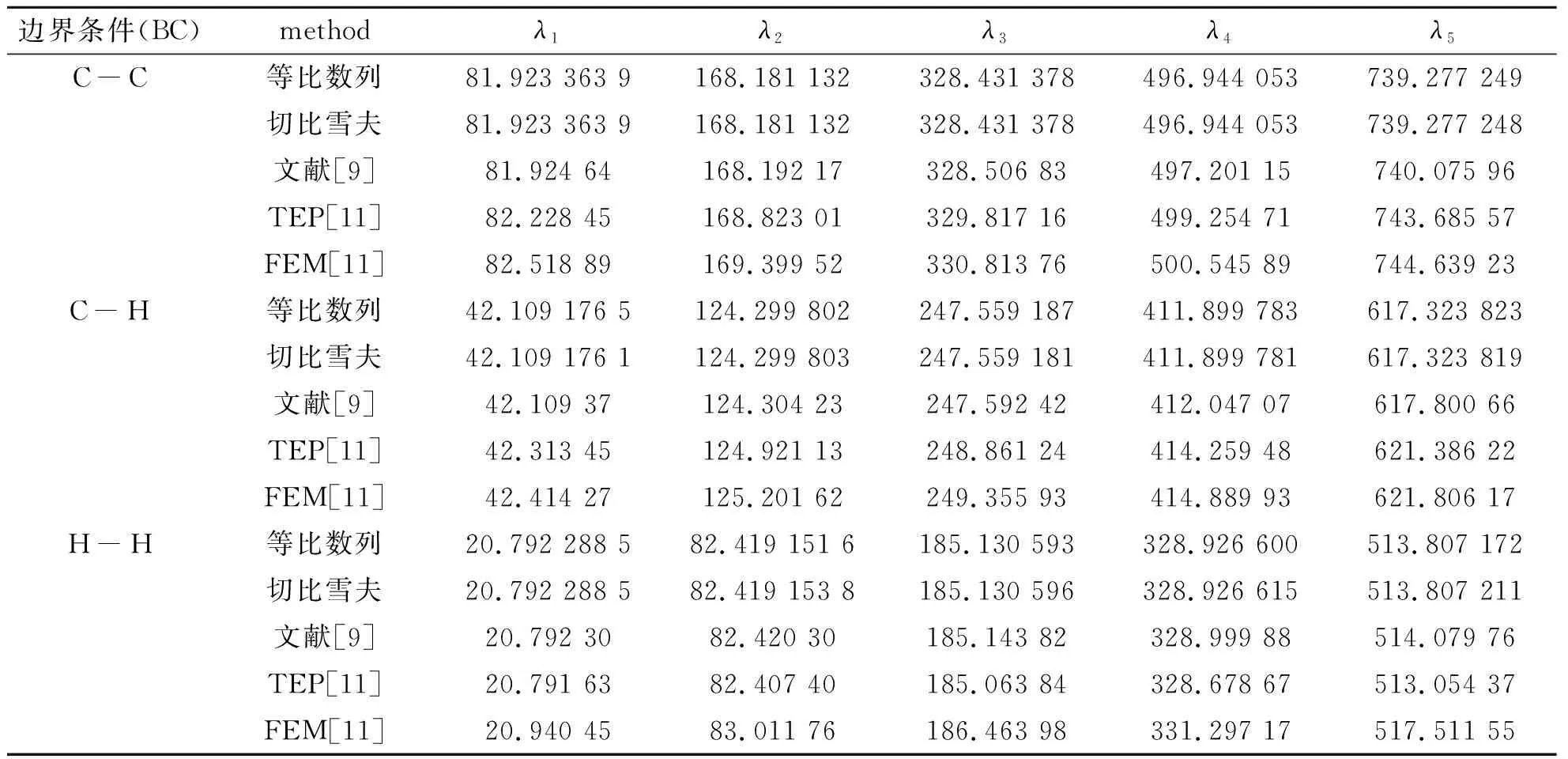
表5 梁的无量纲屈曲临界荷载值(EI(x)=E0I0(1+x)2;c=0;n=32)
弹性地基梁抗弯刚度沿轴向呈多项式函数变化,即EI
(x
)=E
I
(1+x
),(k
=1,2,3),梁左右两端分别在C-C、C-H、H-H边界条件下,对应的无量纲临界屈曲荷载随无量纲地基弹性系数变化的关系曲线图如图2、图3、图4所示。由图2、图3、图4计算结果可知,随着地基弹性系数增大,临界屈曲荷载近似呈线性增长;k
值增大,反映了梁的抗弯刚度EI
(x
)沿轴向自左至右分别呈线性、二次与三次抛物线型变化,相应的临界屈曲荷载数值明显增大,且边界约束越强,其屈曲临界荷载越高。综上可知,弹性地基上Euler-Bernoulli梁的稳定承载力与梁边界条件、抗弯刚度、地基弹性约束强弱等因素密切相关。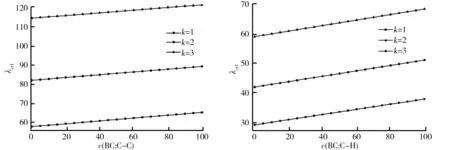
图2 屈曲临界荷载λcr1与无量纲地基弹性系数c的关系曲线(n=32,q1=1.2,C-C边界条件) 图3 屈曲临界荷载λcr1与无量纲地基弹性系数c的关系曲线(n=32,q1=1.2,C-H边界条件)
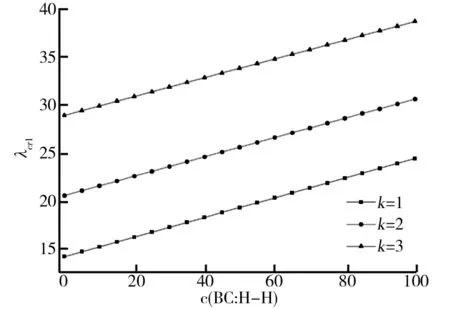
图4 屈曲临界荷载λcr1与无量纲地基弹性系数c的关系曲线(n=32,q1=1.2,H-H边界条件)
3 结论
基于Euler-Bernoulli梁理论,建立了在计算轴向力P
作用下,求解弹性地基上功能梯度Euler-Bernoulli梁屈曲临界荷载的控制方程,运用微分求积法理论,将变系数常微分方程的特征值问题转化为线性代数方程组的特征值问题,一次性地获得弹性地基上梁的屈曲临界荷载。轴向功能梯度变截面Euler-Bernoulli梁临界荷载的控制方程是一组复杂的变系数常微分特征方程,研究方法避免了用迭代方法计算超越方程的困难和繁杂。研究可一次性地计算出弹性地基上功能梯度Euler-Bernoulli梁的临界荷载,变步长等比数列和切比雪夫多项式的根两种布点方式的计算精度等价,且计算值和已有文献计算结果完全吻合,表明了微分求积法求解弹性地基上Euler-Bernoulli梁临界荷载的可行性和精确性。
运用微分求积法计算的结果表明,弹性地基上Euler-Bernoulli梁的稳定承载力与梁的边界条件、抗弯刚度、地基弹性约束强弱等因素密切相关。
