有效独立法在敞车侧墙模态中的应用研究
2021-07-31薛磊马思群孙彦彬张宁博王志丹
薛磊,马思群,孙彦彬,张宁博,王志丹
(大连交通大学 机车车辆工程学院,辽宁 大连116028)
敞车在我国的铁路货运中具有很大的通用性,在货运车辆的组成中,敞车的占比也是最大的。由于重载列车带来的巨大经济效益与社会效益,对敞车等重载列车的研究一直是铁道运输研究的热点。提高车辆的总体设计水平、提高承载能力是当下迫切需解决的重要问题。
模态特性作为车辆结构的固有特性,不会随外在施加的载荷而改变,但车辆结构所产生的细微变化会影响频率的大小[1-2]。车辆的模态可以通过理论计算和试验两种方式获取。对于模态仿真计算,最核心的一步是建立一个正确的模型,过去计算机技术并不先进,所建立的模型一般会做较多简化,近几年随着计算机技术的快速发展,科研活动中越来越注重模型的细化。在模态试验测试中,确定传感器布置的位置和数量是关键一步。优化传感器布置的位置和数量的方法有很多,有效独立法[3-5]是其中使用领域广泛且整体研究进展相对成熟的一种。本次研究中把C70E型敞车作为仿真计算和试验测试的对象,对敞车的侧墙分别进行了有无质量点下的有限元仿真模态计算与模态试验测试分析,证实了模型的正确性与质量点的有效性,确定出基于有效独立法对敞车侧墙进行传感器布置的方案有效、可行。
1 两种模型的模态仿真分析
1.1 侧墙有限元模型的建立
建立一个较好的有限元模型可以使仿真结果更加准确,模型越符合实际形状,仿真结果的精确度越好。但实际的机械结构错综复杂,所受的边界条件往往也是多种多样,普通计算机的性能有限,如果建立的模型太过复杂,会导致计算机难以求解甚至根本无法求解,所以本着对计算准确性影响可以忽略的原则,对模型进行合理简化十分必要。
由于铁路敞车的侧墙呈二分之一对称,本着对称性原则,且在不影响计算结果的情况下,在SolidWorks中建立敞车侧墙的二分之一模型,并忽略帆布钩等不影响计算结果的小零件。
为了使之后建立有限元模型更为便捷,在三维建模的过程中直接采用了以中面为准的曲面建模,形成的三维模型如图1所示。

图1 二分之一侧墙三维模型
构建好的模型需在HyperMesh中检查自由边、T型边和共享边是否符合实际情况,确认无误后利用软件二维单元批处理划分功能进行网格划分,划分前首先对单元质量进行控制设定,如图2所示,单元大小为40 mm。
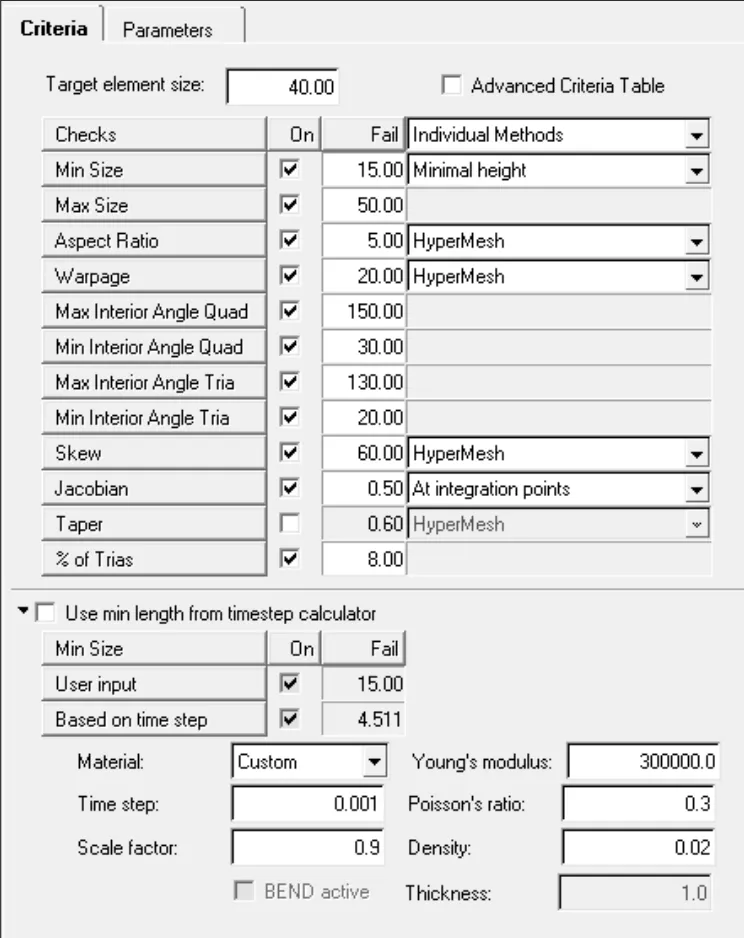
图2 批处理划分时单元质量控制参数
Hypermesh的批处理网格划分功能可以按照单元质量的约束要求不断重复迭代地进行网格划分,直至满足设置的网格质量需求。在Hypermesh批处理网格划分后,对所有单元赋予单元类型与厚度,单元类型为shell181,并将二分之一模型映射为整个侧墙模型,共划分了100282个单元。
在以往的研究中,考虑到侧墙上的所有能够开关的车门相对于车身整体来说质量较小,对车体力学能力的影响较小,大多学者选择忽略车门质量简化计算。
本次为了更加精细地建模,在建立有限元模型时采用了以质量点和刚性单元代替车门的方式,且对其质心位置进行严格的标定,并将质量点设置在质心处。同时为了对比分析,也建立了无质量点和刚性单元的第二种模型。如图3所示。
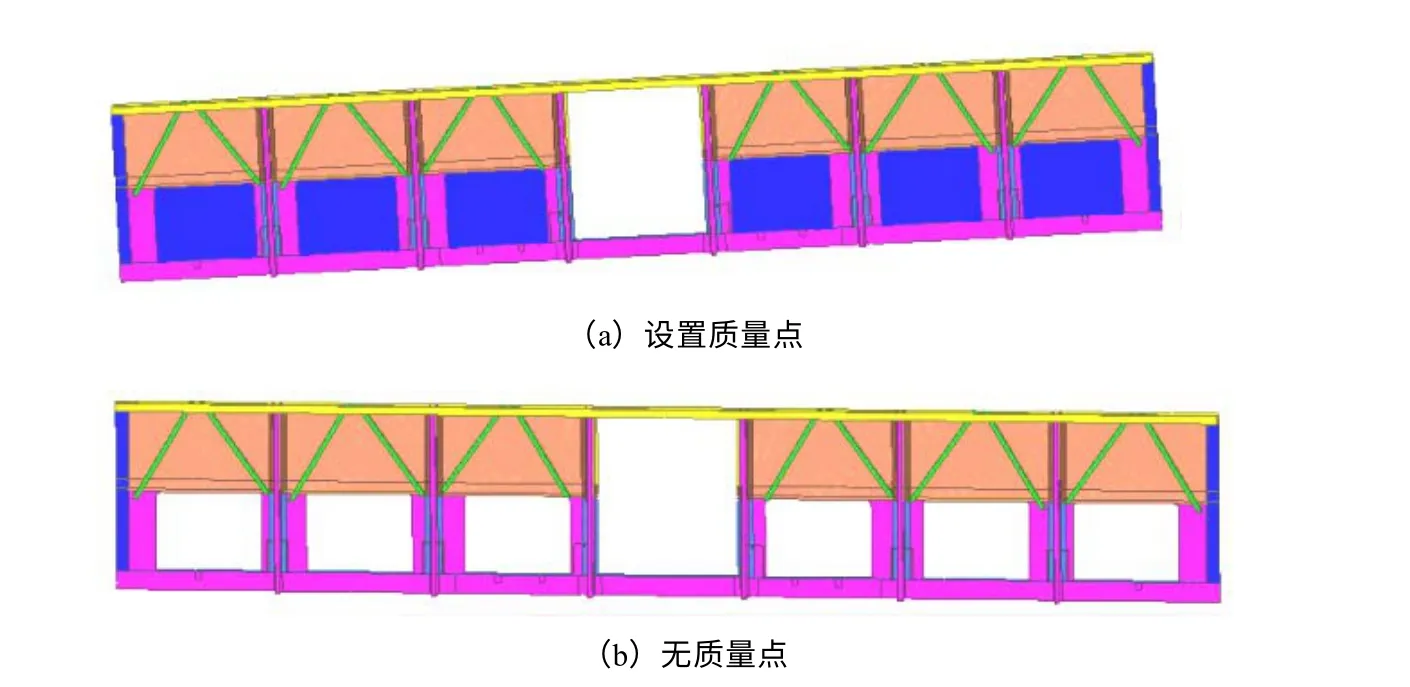
图3 侧墙映射后的有限元模型
1.2 模态仿真基本理论
模态特性是敞车以至于各种机械装备的固有振动性质,模态分析所得到的频率等数据是对机械装备进行承载分析、提高使用可靠性的重要依据。通过对结构的模态分析可以确定机械装备上各位置点的位移变化,预测在特定频率范围之内机械装备实际运行时的振动,提高机械装备的使用寿命,防止共振造成危险发生。其主要原理为:
机械整体结构的动力学方程式为:
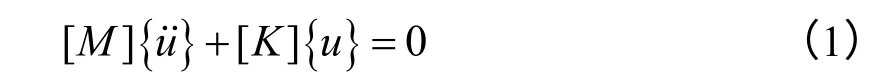
式中:{}u˙˙为节点的加速度矢量;[ ]M为一矩阵表示的质量;{}u为节点的位移矢量;[]K为一矩阵表示的刚度。
对于一个线性的机械系统来说,结构的自由振动以简谐形式表示为:

式中:{}iφ为一特征向量对应第i(i=1,2,…,n)阶的模态振型;iω为第i阶固有振动频率,rad/s;t为时间,s。
将式(2)代入式(1),可得:
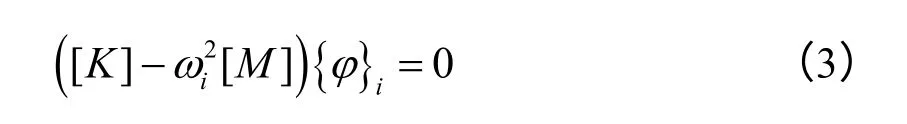
为使式(3)有解,则特征方程的值需等于0,即:

求解式(4)可得特征值,即2iω的值,将特征值代入式(3)可得特征向量,即{}iφ。
最终由软件输出:

式中:f i为机械装备第i阶固有振动频率,Hz。
1.3 车体模态仿真计算结果
将两种模型分别导入ANSYS软件中进行模态计算,所选取的工况均为敞车侧墙在正常空载工作情况下。在ANSYS软件中,本次研究采用软件中默认的计算结果提取方式:Block Lanczos法[6],这种方法在使用时收敛速度比较快,对计算机的性能需求低。
对两种敞车侧墙模型计算完成后,分别求得1~5阶模态计算结果,如表1所示,第4阶模态振型如图4所示。
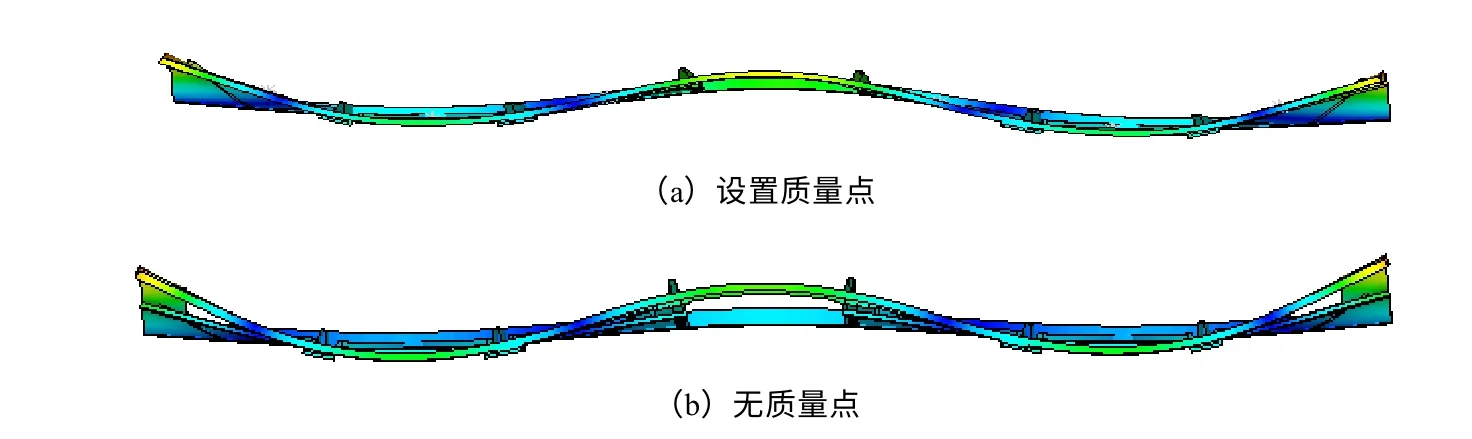
图4 敞车侧墙第4阶模态振型
从表1可看出,在有或没有设置质量点的两种情况下,模态振型描述基本一致,但振动频率有所不同,设置质量点时比无质量点时的振动频率整体更低一些。
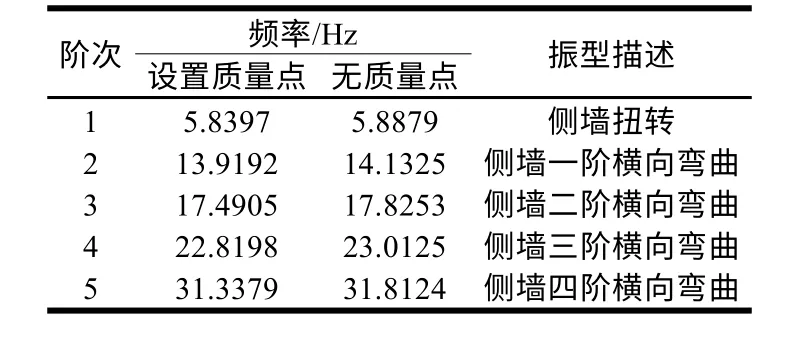
表1 敞车侧墙仿真计算结果
2 敞车侧墙的试验模态分析
2.1 有效独立法基本原理
各类结构的参数识别和状态评估都是由传感器收集实时信息传递至计算机上,因此传感器的布置必须具有高效率,且兼具合理性[7]。所以在对敞车侧墙进行传感器布置时,基本原则是利用能获得的测点尽可能更多地获得数据,反映列车特性。有效独立法(EI法,Effective Independence Method)作为迄今应用最广泛、技术最成熟的一种传感器布置方式,其主要优化思路是由获取的结构模态向量推导出模态振型矩阵(Fisher信息矩阵),确定所有可布设传感器的测点对模态振型矩阵独立性的贡献度,并进行排序,然后通过不断地迭代计算,逐步删除推动模态振型矩阵独立性能力较小的测点,以此来不断优化信息矩阵,这样保证了传感器采集的数据所得到的模态振型之间相互独立,达到最少传感器获得最多数据的目的。其原理如下。
模态测试过程中,需先获取机械结构的模态振型,且所施加激励足以产生模态振动,则:

式中:Pk为传感器获取的数据;q为模态振型坐标,表示未识别因子;矩阵Nk为获取的模态振型简化形式。
若考虑噪声,则:

式中:M为噪声,其方差为。
求解式(6)中q的最小二乘解为:

由于实际可布设传感器的节点数量远多于传感器实际布置数量,所以目的为通过此方法求出q的最优解,使模态振型矩阵最大地维持线性无关。对偏差进行估计时,其协方差矩阵表示为U,构建矩阵E,则:

式中:R为Fisher信息矩阵。
假设在进行模态试验时,环境中被采集的噪声之间相互独立,则:

式中,矩阵Q的一种表示式为:
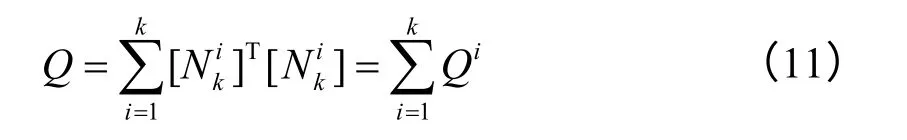
式中:Qi表示对于模态矩阵第i个测点自由度所贡献的量大小,其中部分自由度所产生的贡献较小可以忽略不计并排除。
矩阵Q有特征方程,其特征值和特征向量分别为λ和Ψ,求解特征方程可得:

进而求得矩阵E为:
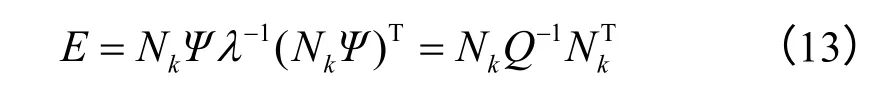
将矩阵E实施变化,右乘单位矩阵I,并表示为:

不难看出,E2=E,所以矩阵E的特征值只能为0和1,其所有对角线元素Eii都体现对矩阵Nk的秩所贡献大小,且0≤Eii≤1。若Eii=0,则这个测点在捕捉目标模态时贡献度较小,予以忽略;相反,Eii=1时,需要保留。
EI法是通过迭代筛选,不断删除有效性较低的布置节点,直至剩余节点满足试验要求数量时停止迭代操作,即目标模态在布置节点满足要求且最少的情况下维持线性无关。
2.2 基于EI法的敞车侧墙传感器布置
通过Hypermesh的批处理网格划分对敞车侧墙进行有限元网格划分,得到整车模型的节点总数为97406,之后对所有节点进行筛选。由于边界位置的节点不便于放置传感器,所以首先排除这类节点。考虑到剩余节点的有些位置或形状具有特殊性,结合敞车车体的结构并联系实际情况,对于一些不便于放置传感器的位置应予以排除,例如表面为凸面,同时表面面积较小的位置,或者空间狭小、传感器放不下的位置。除此之外,对于一些表面安装了较多部件的位置,其构造比较复杂,也不利于传感器的布设,应予以排除。
排除完毕后统计可用测点,将测点数据集合导入MATLAB软件内并开展下一步计算。通过MATLAB软件的编程编辑窗口,结合有效独立法的原理进行编程,对所有剩余的可用测点进行优化筛选。本次优化设置的阀值为24,即通过软件进行不断计算得到24个测点的位置。首先构造出模态振型矩阵,之后由软件计算出可用测点中的每个测点对模态振型矩阵独立性的贡献度,将计算出的各个测点的贡献度绘制成曲线图并呈现出来。在曲线图中对比得到贡献度明显高于其余测点的位置,由EI法理论可知,在这些位置上布置可达到最优效果。流程如图5所示。

图5 基于EI法的传感器布置流程图
2.3 试验模态分析原理概述
模态试验发展较早,随着近些年试验仪器和计算机技术的快速发展,模态测试的精度和效率不断提高,同时各种先进的方法也随之不断涌现。最小乘复指数法(LSCE,Least-Squares Complex Exponential)以及最小二乘频域法(LSFD,Least Square-based Finite Difference)是应用较好的两种方法[8-9],但这两种方法的抗干扰能力不够好,为了解决该问题,提出了最小乘复频域法[10](LSCF,Least Square Complex Frequency domain),此方法可以更好地排除环境干扰,使试验结果更加准确,是目前公认的比较好的试验方法之一。
PolyMAX模态参数识别法[11-12]是西门子公司以LSCF作为理论基础推出的商用工作模态参数的识别方式,即为本次研究的工作模态试验装置所采用的方法。
2.4 侧墙试验模态测试与结果
本次试验测试的工况与仿真计算一样,为敞车侧墙的工作模态,约束条件设置为车辆空载、正常工作情况。对整个侧墙进行传感器布置时,依据前文基于EI法确定的24个布置位置进行布置,并在LMS Test.lab软件中进行试验数据处理。主要试验设备包括加速度传感器、激励击锤、数据采集仪、计算机等,如图6所示,其中箭头表示数据流向。

图6 试验装置简图
经由软件计算将传感器采集的数据进行处理、转化,获得敞车侧墙的固有振动频率与振型,最终测得数据如表2所示。

表2 模态试验测试结果
通过分析模态置信判断分析可以判断出试验模态测试结果的可信度,试验结束后输出试验模态置信度图,发现试验模态中相同振型的MAC(Modal Assurance Criterion,模态置信度)值均为100%,而不同的试验模态振型之间的MAC值就非常低,这表明试验模态测试的结果比较准确,振型图精确度较高、可靠度较好,并没有生成额外虚假的模态。
观察模态振型图可以看出侧墙中间部位产生较大变形的可能比较大,这容易引起整个敞车车体发生较大变形,降低列车的使用安全性、影响车辆的使用寿命。所以设计敞车时,可以采取加强筋等方式提高侧墙的耐受能力。
如表3所示,通过计算试验模态和两种模型的仿真模态的误差可看出设置质量点时误差最大为3.58%,而工程要求一般定为10%左右,显然符合要求。不设置质量点的模型所计算的频率最大误差为5.02%,也符合工程要求,这说明本次研究建立的有限元模型正确。

表3 两种建模方式的计算模态与试验模态对比
虽然不设置质量点的模型与试验测试结果的最大误差也小于10%,但其整体误差会比设置质量点的模型大一些,从而可判断出,有限元模态仿真计算过程中,如果计算精度有要求,则不可完全忽略车门等自身质量较大的零件。
3 结论
(1)由模态置信判据分析可以判断出试验模态结果的可靠性程度较高、试验模态过程较为正确,由此可以判断基于EI法计算侧墙传感器布置的位置和数量、进而进行模态试验的方式可行性较高,所采集的数据不管是准确度还是全面度都比较可观。
(2)通过对敞车侧墙进行两种模型的模态仿真计算与试验模态分析,并对比结果可以得到如下结论:不论有无设置质量点代替车门质量,计算所得结果的误差均符合工程要求,说明进行仿真计算时忽略帆布钩等小部件,或者在对计算精度要求不高时,忽略车门等本身质量较大、但相对于机械装备整体质量较小的结构,对模型进行适当的简化处理是可行的。
(3)由于直接忽略质量较大的车门结构比设置质量点代替时的误差更大,可得,在有限元模态仿真的过程中,在对试验精度有一定要求的情况下,由于车门等本身质量较大的零件会对模态振动频率产生一定影响,所以不适合直接做忽略处理,以质量点代替并以刚性单元连接,且质量点的位置设置在零件的质心处是一种提高仿真精度和结果可靠程度的方式。
